橋梁抗震設計中的結構動力學理論及計算分析
楊茂召
(招商局重慶交通科研設計院有限公司,重慶 212000)
一、工程概況
該項目的施工范圍為k0+900~k13+600、k27+400~k46+800,項目內需要建設15座橋梁,橋梁的總長度設計為17.39km,橋梁的跨徑主要是分為三種規格:20m、30m、40m。其中20m跨徑的橋梁設計為預制裝配式箱梁,30m、40m跨徑的橋梁設計為預制裝配式T梁,橋梁下部結構形式主要是兩種不同類型:三柱式橋墩與雙肢矩形橋墩;結合設計圖紙來看,橋臺設計采用輕型肋板臺。橋墩的高度最高可達到89m,橋梁的最大縱向坡度為5%。對于橋墩高度超過40m,且主跨長度為40m的T梁設計使用墩梁固結結構,這樣可以在最大程度上降低地震與行車荷載對橋梁結構造成的負面影響。
結合前期勘探報告來看,橋梁所處的位置地下結構中存在泥石流堆積物、滑坡堆積物、殘破積物、火山巖、變質巖、沉積巖及巖漿巖。橋梁建設沿線剛好位于歐亞板塊與印度板塊的銜接區域,近些年來,該區域內的底層活動較為頻繁,且地震事故出現的頻率比較高。結合《中國地震動參數區劃圖》(GB18306—2015)內容來看,該區域的地震加速度達到了0.15g,區域內的地震烈度屬于是Ⅶ度,地震動反應譜特征周期為0.45s。
二、橋梁抗震設計理論分析方法
橋梁抗震設計理論知識其實就是研究地震對區域內結構物造成的動態效應,將理論知識運用在結構中的地震波來獲取運動微分公式,借助運動微分公式計算出結構物在地震作用下的移動速度、加速度及位移量,而后可以獲取到結構的地震響應。現階段,國內外學術界對于橋梁抗震設計理論的研究主要是有以下幾種方法:反應譜法、靜力法和時程分析法。
(一)靜力法
該分析方法的理論基礎是以結構物與地表振動具備相同的效應,結構物受到荷載就是因地表出現振動對結構物造成的一種慣性作用力,其具體的表達式為:
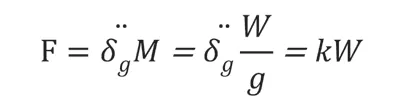
(二)反應譜法
這種分析方法是將單一自由度體系下的振動計算原理應用在多自由度體系下的地震分析場景中。通過對結構動力的特點進行分析,計算出結構各個部分的階振,然后不同部分的階振所面對的地震作用計算出來,最終以標準化的組合方式來計算出地震作用效應。
1.反應譜基本原理
單質點體系是由于受到地表巖層運動而形成的,單質點振動表達式為:

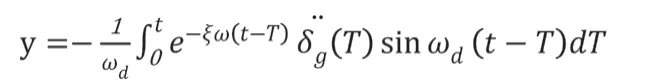
將以上表達式進行一次微分、二次微分,可以獲取到單質點振子的地震加速度與相對速度反應積分表達式。通常情況下,地震的阻尼比都非常小,完全可以忽略不予以計算。故積分表達式應該是:
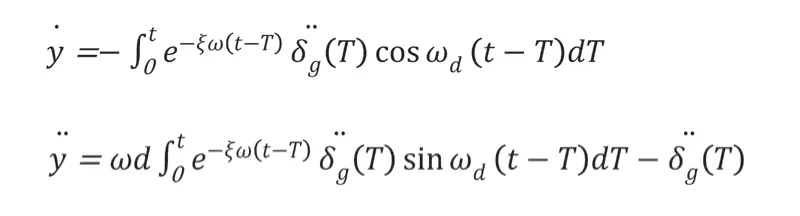
可以理解為,地震作用下形成的加速度δg屬于是一個不規則的表達式,可以利用數據積分獲取到地震加速度的反應曲線,多個單質點振子在相同的地震加速度δg(T)下,進一步計算可以獲取到結構物的相對位移y,相對速度,絕對加速度,以此為依據計算出最大值,從而繪制出Ti為橫坐標、不同阻尼比為參數的的譜曲線,這就是反應譜。
2.反應譜理論的地震力計算
反應譜分析方法比較簡單,主要是有兩部分組成。首先將地震反應譜函數全部整理出來,然后對結構物的振動形式進行分解。計算出在地震作用力最大的情況下,結構物抗震性能的第一步,利用單質點體系振動函數可以獲取到最大地震作用力的表達式:
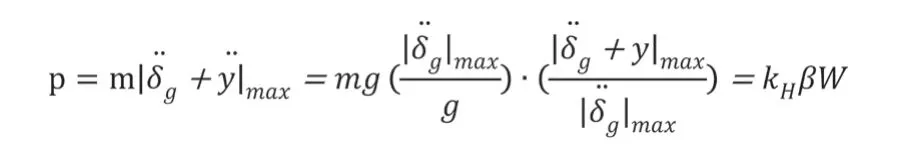
以上表達式中:g是指重力加速度;W是指總質量;定義為水平地震系數:
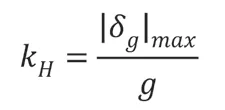
反應譜方法分析地震力的基本原理如上述表達式展示內容,在實際分析的過程中,需要涉及到兩方面的影響因素:
(1)水平地震系數,簡單而言就是取值。當抗震防裂度的要求不同時,那么其所對應的水平地震系數也存在一定的差異。現階段,我國鐵路工程的抗震要求為:設計烈度Ⅶ、Ⅷ、Ⅸ度的k分別取值為0.1、0.2和0.4。
(2)譜曲線的確定。不同震波帶來的震波作用都存在差異性,且這種震波作用的規律比較復雜,無規可循。進一步而言,本文所使用的反應是結合既往發生的地震加速度案例記錄所得,將整理所得的地震加速度數據經過特殊處理,從而形成了動力放大系數。
3.引入結構綜合影響系數
反應譜研究理論是將彈性變形結構作為前提基礎展開分析的,因此反應譜的分析活動具備顯著的線彈性特點。結構物處于彈性變形過程中時,會逐漸轉變為塑性變形狀態,受力特點與結構特征會發生明顯的變化,同時其對于地震的響應也會造成巨大的影響,結構處于塑性變形狀態時,其能夠抵抗一定程度的地震作用,在這種情況下需要納入一個技術參數對結構的塑性變形進行分析,簡單而言就是加入綜合影響系數CZ。
4.反應譜組合方法
在分析地震作用時,需要對多個振型疊加計算,不同的振型所引起的地震響應效果存在較大差異,所以需要對振型進行組合,振型組合方法比較多,目前國內外使用較為頻繁的方法有SRSS、CQC方法等。
(三)時程分析法
1.時程分析法概述。這種分析方法主要是對結構抗震動態化設計過程進行分析,將地表地震的加速度對結構物運動方程進行積分,由此可以獲取到每一個質點隨時間變化的相對位移量、速度及加速度。這種分析方法在全球范圍內運用頻率比較高。
2.時程分析法理論基礎。這種分析方法的核心理念認為應該將結構物的運動方程納入到地震荷載中,簡單而言就是地震作用下的加速度曲線導入至結構的運動方程內,然后借助數值積分法來計算出地震作用的響應。積分過程中,將地震作用的時間劃分為多個不同的時間段逐一積分,從結構運動的初始化狀態作為起點,將下一段的時間節點的初始化條件作為上一個節點的結果,以此類推不斷積分,直至地震作用結束。
3.時程分析法執行步驟。(1)將結構在地震作用下的運動方程劃分為多個微小的時間間隔Δt;(2)若在危險時間間隔中的位移量、速度及加速度之間存在一定的關聯性,可以使用特定的方法求解出結構運動的具體情況;(3)通過逐步接分的方法,以初始化條件來逐步求解出下一個時間節點的位移量、速度及加速度,從而高效地求解出結構運動方程。
三、反應譜統一計算方法
結合各國現行的抗震設計管理規標準對于反應譜設計的管理要求來看,雖然各國現行的管理規范存在一定的差異,但是設計反應譜的曲線結果是一致的,也就是結構自振周期從初始化開始緩慢增大,同時反應譜也會逐漸增大,增大至一個標準值以后,開始緩慢地降低。
結合理論研究分析來看,反應譜的曲線大致由三部分構成:上升段、平臺段、下降段;其中,下降段大致可細分為兩個段落;這一研究結果與各國現行的管理規范保持一致。
此外,各國現行的抗震設計管理規范中,設計反應譜還存在一定的差異之處,與理論研究存在一定的出入,其具體表現在:
上升段:以我國現行的抗震設計管理規范來看,上升段與平臺段之間的連接點結構自振周期為0.1s,西方發達國家的抗震設計管理規范則是依據于現場地質條件勘察進行確定。站在理論層面來看,連接部位的周期結合不同的場地地質條件進行分類處理更具備合理性,同時與實際情況更為貼切;但是結合實踐情況來看,在實際運用的過程中必然會大幅度增加工程量,常規悉尼港的結構自振周期基本上都是大于0.1s;所以本文將連接部位的周期確定為0.1s,以此減小設計活動的工作量。
平臺段:以我國現行的抗震設計管理規范來看,平臺段的高度基本都控制在2.25,西方發達國家的抗震設計管理規范則是將平臺段的高度確定為2.5。本文將平臺段的高度確定為2.25,對設計抗震存在一定的不安全影響,所以應該適當的將平臺段的高度提升至2.5。
下降段:以我國現行的《公路橋梁抗震設計細則》規范來看,下降段除了一個曲線段以外,還存在兩個曲線段。但是結合理論層面來看,其主要是分為兩個曲線段。
第一曲線段的衰減指數為0.9,其他曲線段取值為1。結合實際情況而言,取值為1相對更為安全。
所以,結合強震反應譜理論,本文提出了以下計算公式:
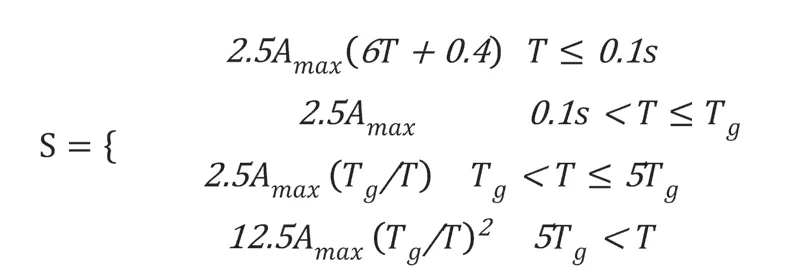
以上表達式中:Tg是指場地特征周期;Amax是指抗震設防加速度值。以Tg=0.35S為例,設計反應譜曲線如圖1所示。
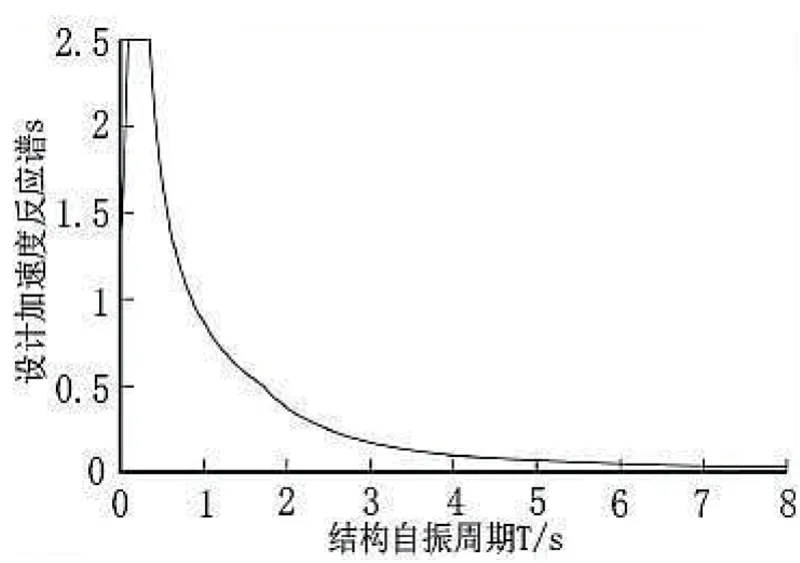
圖1 本文提出的歸一化設計反應譜
研究結論:設計反應譜的曲線主要可細分為3種類型:上升段、下降段、平行段;當地震結構自振周期增大以后,那么設計反應譜曲線中的下降段則可以細分為兩個曲線段;此次研究過程中所提出的反應譜計算方法比較簡單,且力學原理非常清晰,具有良好的應用效果。
四、結語
從橋梁地震災害中不斷總結設計經驗,不斷對理論基礎進行優化,促使我國橋梁抗震設計理論越來越完善,本文主要是對橋梁結構抗震體系、抗震設計方法進行深入研究分析,對多種地震結構設計方法進行介紹,設計人員在實際對橋梁結構進行設計時,應該結合施工現場的地質條件、抗震級別進行設計。本文所構建出來的設計反應譜對于大跨度橋梁低自振頻率結構具有一定的參考價值。

