基于靜力數據下RBF神經網絡梁式模型修正★

劉海祥，謝志祥，黃長龍，張 衡

（長江大學城市建設學院，湖北 荊州 434023）

0 引言

數值仿真模型修正計算在航天航空、橋梁等領域有著廣泛的應用。有限元模型修正利用實際測試得到的靜態或動態信息與理論模型得到的分析結果進行對比，通過對參數的修正使得理論模型更加精確、符合實際。在工程結構領域，一方面建筑結構在長期的使用過程中會遭受各種環境荷載作用、溫度應力的侵蝕和影響，使得建筑構件老化、材料性能發生變化，使得構件的實測值與模型的計算值存在較大誤差；Shankar Sehgal綜述了FE模型誤差的原因：邊界定義誤差、材料屬性誤差、連續體呈分散性及形體不易建模［1］。

數值仿真模型計算領域：例如蔡國平等將神經網絡算法引入有限元模型修正中，該方法能夠較快地收斂到全局最優解［2］。孟慶成等將灰色系統理論和神經網絡算法結合，能夠適應小樣本、數據不全的情況［3］。但是，以上基于神經網絡的模型修正都是基于動力試驗的，基于靜力試驗的研究很少。其中袁旭東等利用靜力測量結果對一五榀桁架結構采用了改進動量的BP神經網絡算法，其結果表明測量數據不完備條件下，神經網絡模型具有很強的魯棒性、模型依然具有較高的準確性［4］。

本文提出了利用ABAQUS有限元軟件建立的簡支梁模型，提出一種基于靜力數據下神經網絡的模型修正方法，并運用一種基于靜力凝聚下的徑向基神經網絡模型修正方法。最后利用RBF神經網絡與BP神經網絡進行比較，驗證該算法的有效性。

1 靜力凝聚法原理

靜載荷作用下結構的初始靜態平衡方程可以表示為：

其中，k0為初始狀態下的N×N維全局剛度矩陣；U0為N×1維的初始位移向量；F0為N×1維的靜態載荷向量。

對于FE（有限元）模型，全局剛度矩陣的變化可以表示為元素剛度矩陣展開矩陣的線性組合，如下：

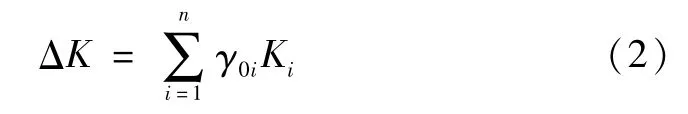
其中，n為總結構元素的數量；γ0i為結構元素更新因子，即結構參數的變化速率；Ki為單位元素剛度矩陣的N×N維擴展矩陣，其中其他部分為零。

假設結構剛度矩陣可以更新為矩陣，并被寫入的形式：

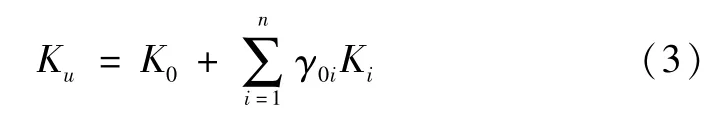
考慮到在初始狀態和更新狀態下的負載是相同的，我們可以有：

其中，Uu為測量得的位移向量。

假定剛度矩陣中的平動分量和轉動因子已經相互分離，寫成分塊形式：

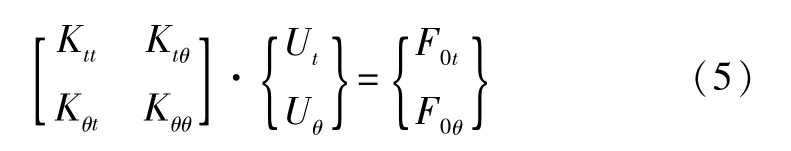
其中，t為平動分量；θ為轉動分量，下標代表相應元素的子矩陣。

采用靜力凝聚法對自由度進行壓縮：假如產生作用效應的荷載中忽略了轉動因素的影響，即Fst=0。把公式代入到上面的方程，那么可以得到轉動自由度的表達式：

將式（6）代到首個矩陣表達式中：

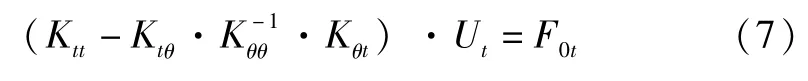
式（7）可以寫成：

即式（4）。

通過式（8）可以求出豎向撓度值。

2 徑向基神經網絡概述

人工神經網絡強大的信息處理能力應用在許多領域，其強大的非線性映射能力、自適應、自學習和容錯性能夠讓神經網絡從大量的歷史數據中進行聚類并學習，找到某些行為變化的規律。RBF神經網絡是一種前饋式神經網絡，具有最佳逼近和全局最優的優點，相比于BP神經網絡不存在局部最優問題。Powell于1985年提出了基于多變量插值的徑向基函數方法，之后Broomhead和Lowe在1988年首次將RBF應用于神經網絡設計、構建徑向基函數神經網絡［5］。

3 梁式結構模型修正實例

3.1 實體模型

在實驗室建造一根預應力混凝土簡支梁，簡支梁的設計示意圖如圖1所示。混凝土設計強度C30，非預應力鋼筋采用HRB400級鋼筋，預應力鋼筋采用1860級鋼絞線，箍筋采用Φ6 mm的光圓鋼筋，間距150 mm。圖1為混凝土實體梁加載實驗裝置圖，在彈性范圍內對梁進行大小為5 040 kN的集中荷載加載試驗（不卸載），測量其撓度。兩個集中加載力的位置及測點示意圖如圖2所示。由于計算模型的自由度總與現場測試的數目不吻合，這里采用靜力凝聚法對模型自由度進行縮減，使其數目相符［6］。

圖1 實驗加載裝置圖

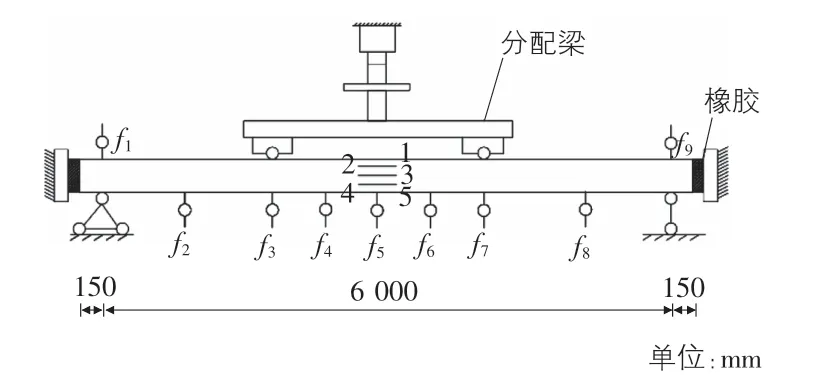
圖2 測點的布置

3.2 基于ABAQUS的有限元模型［7-8］

基于ABAQUS分析的模型主要有：分離式和整體式兩種。本文在有限元中采用整體式的建模方法，能夠有效避免因為單元細分導致的應力奇異問題，有利于提高整體計算的收斂性性能。圖3為試驗混凝土簡支梁尺寸及配筋示意圖。表1為混凝土簡支梁初始材料參數表，混凝土單軸受壓應力應變采用混凝土設計規范（塑性損傷模型）。

圖3 簡支梁實驗圖及配筋圖

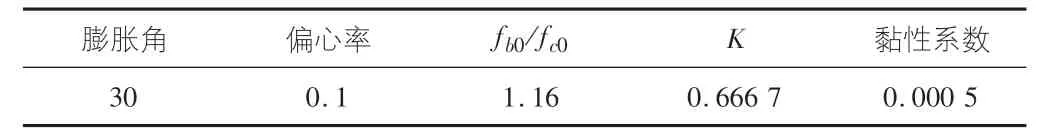
表1 簡支梁初始材料參數表

3.2.1 混凝土相關參數計算

混凝土材料本構關系采用Saenz和Sargin模型：

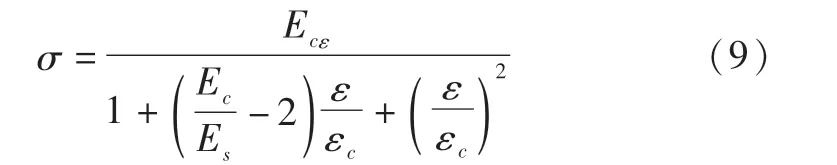
其中，ε為應變；Ec為變形模量；Es為彈性模量。

其中：

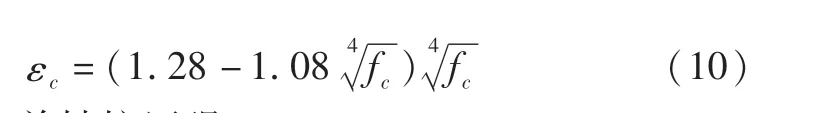
其中，fc為單軸抗壓強。

本文采用混凝土的塑性損傷模型［9］，由于實際的鋼筋混凝土結構構件多，鋼筋布置十分復雜，如果考慮混凝土壓碎時，計算結果在非線性階段撓度-位移曲線偏差較大、結果容易發散；而不考慮混凝土壓碎，則模型計算結果收斂，因此這里采用的是加載時未開裂階段的撓度-位移加載數值。

3.2.2 模型及網格劃分

采用sweep網格劃分技術，劃分網格前，首先要指定各個部件的網格單元類型。為了避免出現較嚴重的沙漏現象和網格扭曲，打開網格扭曲控制開關，同時沙漏控制設置為增強。鋼筋骨架的單元類型選為T3D2，其余設置默認，網格劃分后的簡支梁見圖4。

圖4 有限元模型網格劃分

3.2.3 模型加載及job分析步

在有限元軟件load模塊中施加邊界條件和荷載，按照簡支梁邊界條件，左邊加固定約束、右邊加豎向鏈桿，荷載加載方式選擇施加豎向的位移，模型不考慮扭轉的作用。

在job分析模塊選擇完全分析、重啟動分析，提交分析作業，模型梁的變形的加載見圖5。模型加載計算完畢后，進入后處理模塊選取測點并輸出點的撓度值。通過對比測量結果與模型位移計算結果，發現實測撓度與計算撓度相差較大，故利用神經網絡對結果進行修正以便使模型與實際相符。

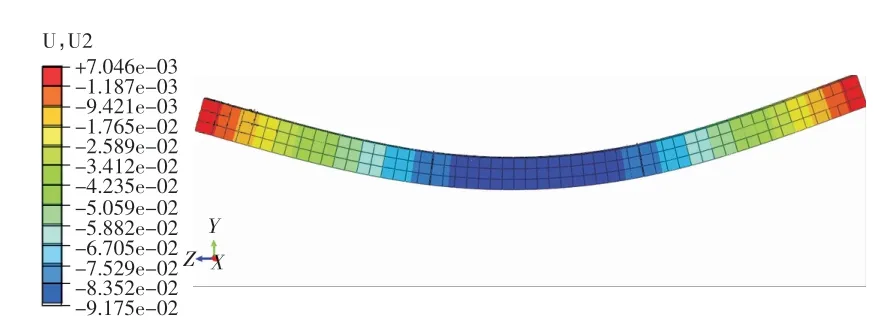
圖5 梁的變形圖

4 徑向基神經網絡修正［10］

進行靜力荷載試驗，取構件在一種工況條件下的多組撓度數據，采用基于RBF神經網絡結合靜力數據對該梁式結構的初始模型參數進行修正。為了驗證RBF神經網絡的修正性能，采用MATLAB神經網絡工具箱中的BP神經網絡進行兩者的對比分析，驗證基于徑向基神經網絡有限元模型修正的可行性及實用性。

基于RBF網絡模型修正步驟［11］如下：選取待修正參數，根據專家經驗的方法，選取對結構特征響應量（本文采用靜載工況的撓度值）靈敏度高的設計參數作為待修正參數，最后利用神經網絡輸出參數修正的結果。

4.1 修正參數的選擇

有限元模型修正就是通過實測響應與理論模型計算得到的結果進行對比修正，使得修正后的理論模型數據滿足精度要求。在建立有限元模型修正時一般選擇物理參數（彈性模量E、截面積A以及抗彎剛度EI）作為待修正的參數。如果將所有的物理參數都作為修正參數，雖然模型修正的精度得到保證，但是模型的計算量大、效率低，而且分析結果不易收斂。為了提高修正效率，在模型修正前必須要選出對更加結構敏感的物理參數。本文利用結構簡單的簡支梁作為仿真計算的實例，采取工程經驗將截面尺寸、截面慣性矩和彈性模量作為模型待修正的物理參數，利用實測撓度來修正截面尺寸、截面慣性矩和彈性模量，具體數據見表2。

表2 模型參數及區間

4.2 樣本點的選擇

樣本的選擇直接影響神經網絡構建，FEM計算的次數與樣本點的數目具有直接關系。均勻并具有代表性的樣本點數據，能夠更好地滿足計算效率及精度。本文采用均勻樣方設計［12］，建立3參數21水平的神經網絡樣方設計表。

4.3 算法描述

4.3.1 歸一化

將數據歸一化就是將數據映射到［0，1］或［-1，1］區間或更小的區間。導入神經網絡樣方設計表數據到MATLAB矩陣中，調用MATLAB函數mapminmax歸一化導入的樣本數據。

4.3.2 創建及仿真訓練

通過MATLAB神經網絡工具箱中函數newrb（P，T，goal，spread，MN，DF）函數實現徑向基神經網絡的創建，其中P和T分別代表訓練集的輸入和輸出，goal為均方誤差的目標，SPREED為徑向基的擴展速度，MN為最大的神經元個數。

該徑向基神經網絡每次訓練后再從樣本中提取新的網絡參數、隱含層神經元數目增加，當重復訓練后的神經元數目達到均方差目標時，訓練停止得到需要的徑向基神經網絡。

4.3.3 結果分析

撓度修正前后的比較見表3，計算結果誤差圖見圖6。

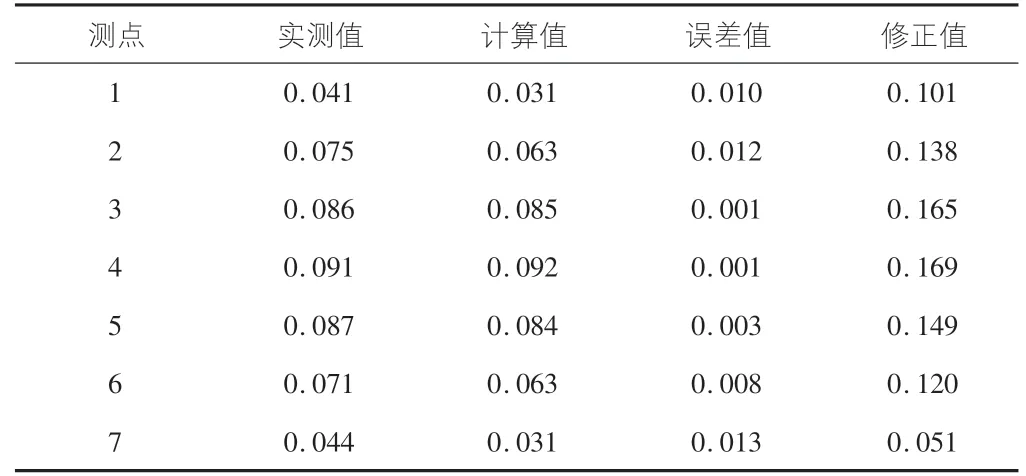
表3 撓度修正前后的比較

圖6 計算結果誤差圖

通過表3，圖6可以發現，用有限元軟件ABAQUS建立的混凝土簡支梁在兩個豎向大小為5 040 kN的集中力加載下產生的撓度值與實測值大致相符合，但還是具有較大誤差。在建立模型的過程中發現，材料參數的定義、邊界條件的設置即使與模型初始參數一致也不能完全模擬出實際的模型結構性能。在利用MATLAB構建的徑向基神經網絡修正后，得到了與實際比較相符的結果，其中相比于BP神經網絡，RBF神經網絡的修正效果更好：與實際結果的誤差均不超過4%（見表4，圖7）。

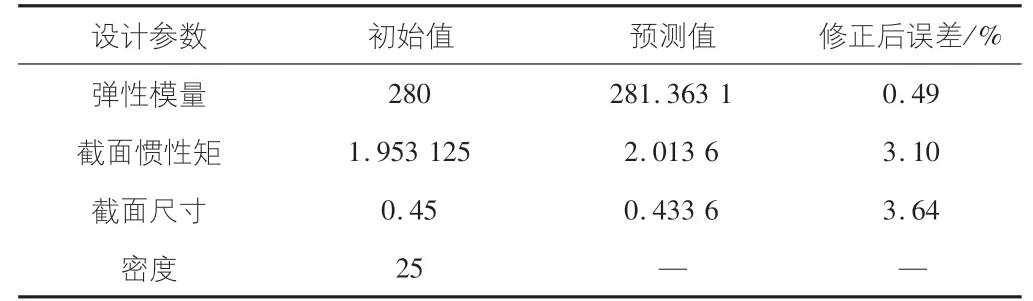
表4 設計參數修正前后的對比

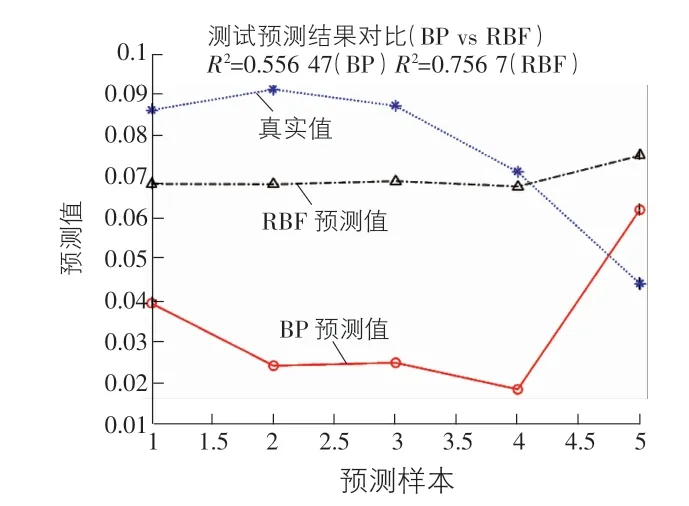
圖7 預測樣本曲線

5 結論

1）利用有限元軟件ABAQUS對一梁式結構進行仿真模擬，發現實測撓度與理論撓度相差較大。采用徑向基神經網絡對靜力數據下的梁式結構進行模型修正，并與BP神經網絡進行對比，修正結果誤差不超過4%，表明了修正結果的有效性。

2）不需要復雜的模型迭代計算，徑向基神經網絡可以將力學的反問題的求解逆為正向求解從而避免非線性和不確定性因素。