尺寸效應(yīng)對(duì)混凝土試塊抗壓強(qiáng)度的影響

周齊洪 張澤宇 唐 莉 楊 暢 彭 昊

（1.四川農(nóng)業(yè)大學(xué)建筑與城鄉(xiāng)規(guī)劃學(xué)院，四川 都江堰 611830；2.重慶市建設(shè)工程質(zhì)量檢驗(yàn)測試中心有限公司，重慶 400016）

關(guān)鍵字：混凝土；尺寸效應(yīng)；試塊抗壓強(qiáng)度；強(qiáng)度轉(zhuǎn)換；高強(qiáng)材料

0 引言

混凝土試塊截面尺寸的增加造成混凝土試件抗壓強(qiáng)度的降低，是混凝土尺寸效應(yīng)的普通表現(xiàn)。既有研究發(fā)現(xiàn)，隨著材料強(qiáng)度的提升，混凝土立方體試塊抗壓強(qiáng)度的尺寸效應(yīng)越明顯[1-3]。尤其是C60以上的高強(qiáng)混凝土，尺寸效應(yīng)造成的立方體抗壓強(qiáng)度折減比例會(huì)顯著提升[4]。蘇捷[5]試驗(yàn)研究發(fā)現(xiàn)，隨著截面寬度的增加，棱柱體的軸心抗壓強(qiáng)度逐漸變小，且提升材料強(qiáng)度會(huì)加速試塊抗壓強(qiáng)度的衰減。日本學(xué)者[6-7]在混凝土圓柱體試塊抗壓強(qiáng)度的試驗(yàn)研究中也獲得類似的結(jié)論。

既有研究還發(fā)現(xiàn)，混凝土試件的長寬比同樣會(huì)引起尺寸效應(yīng)[8]。Mansur等人[9]發(fā)現(xiàn)，隨著材料強(qiáng)度的增加，同截面尺寸的混凝土圓柱體與立方體抗壓強(qiáng)度比也隨之增加。過鎮(zhèn)海[10]通過對(duì)已有122組數(shù)據(jù)統(tǒng)計(jì)分析，發(fā)現(xiàn)混凝土的軸心抗壓強(qiáng)度隨立方體抗壓強(qiáng)度單調(diào)增長，且兩者比值的變化范圍為0.70~0.92。然而，宋中南[11]認(rèn)為，長寬比對(duì)試塊強(qiáng)度的影響主要表現(xiàn)在80MPa以下的試塊強(qiáng)度范圍；當(dāng)材料強(qiáng)度在100~120MPa范圍，100mm的立方體抗壓強(qiáng)度fcu,100與圓柱體強(qiáng)度fcy,100差異不再明顯。

因此，試塊尺寸和強(qiáng)度等級(jí)均是尺寸效應(yīng)對(duì)混凝土抗壓強(qiáng)度影響的重要因素。但不同學(xué)者在主控因素對(duì)混凝土試塊，尤其是高強(qiáng)（高性能）混凝土，抗壓強(qiáng)度的具體影響趨勢(shì)及量化建議上仍存在一定差異。

本文收集1107組既有混凝土試塊試驗(yàn)數(shù)據(jù)，通過數(shù)理統(tǒng)計(jì)回歸分析方法，系統(tǒng)地研究了現(xiàn)行相關(guān)規(guī)程與學(xué)者既有成果在混凝土試塊抗壓強(qiáng)度計(jì)算與轉(zhuǎn)化方法上的精度與可靠性，并重點(diǎn)分析了高強(qiáng)度混凝土的試塊抗壓強(qiáng)度計(jì)算方法。

1 試驗(yàn)數(shù)據(jù)及特征分析

基于國內(nèi)外既有文獻(xiàn)資料[2],[9],[12-36]，本文將整理的1107組混凝土試塊試驗(yàn)數(shù)據(jù)整理成樣本庫，其中包括了四種試塊類型（邊長為100mm與150mm的立方體，150mm×150mm×300mm的 棱 柱 體 及Φ150mm×300mm圓柱體）及對(duì)應(yīng)的抗壓強(qiáng)度。樣本庫的抗壓強(qiáng)度范圍約在18.2~128MPa。

圖1以標(biāo)準(zhǔn)立方體試塊為中介，對(duì)4種試塊類型進(jìn)行分類統(tǒng)計(jì)，獲得了標(biāo)準(zhǔn)立方體試塊與其他3種試塊類型的3項(xiàng)配對(duì)數(shù)組。以fcu,150≥60MPa的樣本標(biāo)定為高強(qiáng)混凝土，則各類規(guī)格的高強(qiáng)試塊均約占各自占比的50%或以上。

2 不同混凝土試塊抗壓強(qiáng)度的轉(zhuǎn)化方法

2.1 混凝土試塊抗壓強(qiáng)度的轉(zhuǎn)化方法

本文共采取了7種相關(guān)規(guī)范及學(xué)者提出的針對(duì)各類試塊的強(qiáng)度轉(zhuǎn)化方法及其適用范圍，包括規(guī)程《高強(qiáng)混凝土結(jié)構(gòu)技術(shù)規(guī)程》（CECS 104:99）[37]和《混凝土結(jié)構(gòu)設(shè)計(jì)規(guī)范》（GB 50010-2002）[38]中的換算公式與高志揚(yáng)[2]、Peterson[39]和馬欣伯[40]各自所使用過的換算方法。

高志揚(yáng)：

Peterson：

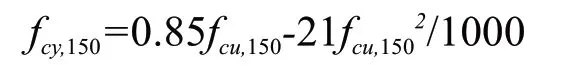
馬欣伯：

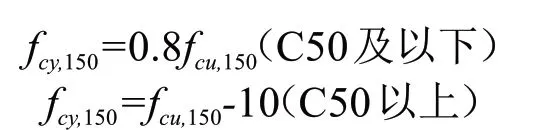
其中馬欣伯的建議方法是綜合了歐洲規(guī)范與美國規(guī)范的優(yōu)化方法。除了國內(nèi)規(guī)范出于實(shí)用性考慮分段系數(shù)法外，上述所采取的試塊抗壓強(qiáng)度轉(zhuǎn)換方法基本滿足了函數(shù)的連續(xù)性。對(duì)于樣本數(shù)據(jù)中部分超出推薦方法的適用范圍的高強(qiáng)試塊，轉(zhuǎn)換方法參考C80轉(zhuǎn)換系數(shù)值。

2.2 立方體試塊之間抗壓強(qiáng)度的轉(zhuǎn)換方法

基于樣本庫a組中100mm與150mm立方體的377組實(shí)測數(shù)據(jù)，依據(jù)CECS 104:99規(guī)程與高志揚(yáng)建議的立方體試塊間抗壓強(qiáng)度轉(zhuǎn)換方法，分別討論兩種轉(zhuǎn)換方法下的立方體試塊強(qiáng)度轉(zhuǎn)化精度。

由圖2不難看出，針對(duì)fcu,150向fcu,100的轉(zhuǎn)化，當(dāng)偏差在±15%之內(nèi)時(shí)，CECS 104:99規(guī)程和高志揚(yáng)方法的數(shù)值占比相當(dāng)，兩種方法的計(jì)算值與試驗(yàn)值總體上偏差均不大，均值與方差整體水平基本一致。

進(jìn)一步通過對(duì)高強(qiáng)試塊間的強(qiáng)度轉(zhuǎn)化精度進(jìn)行對(duì)比分析可以看出，CECS 104:99規(guī)程與高志揚(yáng)方法在±15%內(nèi)偏差分布特征類似，但高志揚(yáng)方法的精度更高。

2.3 棱柱體與標(biāo)準(zhǔn)立方體抗壓強(qiáng)度的轉(zhuǎn)化方法

依據(jù)CECS 104:99規(guī)程與GB 50010規(guī)程的轉(zhuǎn)換方法，針對(duì)b組中120組實(shí)測數(shù)據(jù)，以標(biāo)準(zhǔn)立方體抗壓強(qiáng)度實(shí)測值fcu,150-exp計(jì)算出相應(yīng)的150mm×300mm棱柱體試塊強(qiáng)度fc,150-cal，將其與對(duì)應(yīng)的實(shí)測值fc,150-exp進(jìn)行對(duì)比。

由圖3可以看出，CECS 104:99規(guī)程基本滿足fc,150-cal/fc,150-exp在±15%之內(nèi)，而GB 50010規(guī)程的計(jì)算值評(píng)估整體偏保守。研究高強(qiáng)范圍內(nèi)尺寸效應(yīng)對(duì)混凝土試塊抗壓強(qiáng)度影響，基于CECS 104:99規(guī)程的高強(qiáng)樣本數(shù)據(jù)隨fc,150-cal/fc,150-exp比值呈正態(tài)分布，偏差±15%以內(nèi)的數(shù)據(jù)占比97.3%。GB 50010規(guī)程除了計(jì)算值保守外，僅有75.7%的數(shù)據(jù)偏差在±15%以內(nèi)。

綜上所述，CECS 104:99規(guī)程的推薦方法更適合用于標(biāo)準(zhǔn)立方體與棱柱體之間的轉(zhuǎn)化。

2.4 圓柱體與標(biāo)準(zhǔn)立方體抗壓強(qiáng)度的轉(zhuǎn)化方法

依據(jù)CECS 104:99規(guī)程、馬欣伯及Peterson推薦的轉(zhuǎn)換方法，針對(duì)c組中57組實(shí)測數(shù)據(jù)，以標(biāo)準(zhǔn)立方體實(shí)測值fcu,150-exp計(jì)算出相應(yīng)的圓柱體抗壓強(qiáng)度計(jì)算值fcy,150-cal。

以±5%偏差率為梯度，圖4統(tǒng)計(jì)了各偏差率內(nèi)的數(shù)據(jù)分布特征。不難發(fā)現(xiàn)，Peterson方法的整體均值、方差、偏差±15%內(nèi)數(shù)組占比均為最優(yōu)，其次為馬欣伯推薦方法，CECS 104:99規(guī)程整體表現(xiàn)相對(duì)最差。針對(duì)高強(qiáng)試塊，雖然3種推薦方法的轉(zhuǎn)化精度均有所提升，但Peterson方法仍具有最優(yōu)均值和最佳穩(wěn)定性。

基于上述分析結(jié)論，選取15%以內(nèi)保證率最高的換算方法，可確定：立方體試塊間抗壓強(qiáng)度轉(zhuǎn)換方法、棱柱體與標(biāo)準(zhǔn)立方體抗壓強(qiáng)度轉(zhuǎn)化方法均采用CECS 104:99規(guī)程，標(biāo)準(zhǔn)圓柱體與標(biāo)準(zhǔn)立方體抗壓強(qiáng)度轉(zhuǎn)化方法采用Peterson推薦方法。

3 尺寸效應(yīng)對(duì)混凝土抗壓強(qiáng)度的影響

圖5中的離散點(diǎn)展示了a、b、c三類試塊分組的實(shí)測比值與試塊強(qiáng)度之間的關(guān)系。

由圖5可以看出，隨試塊尺寸或體量的增大，各比值呈逐漸減小的趨勢(shì)，同時(shí)，隨著材料強(qiáng)度的提升，圓柱體和棱柱體的強(qiáng)度衰減程度更明顯。Peterson方法和CECS 104:99規(guī)程分別在立方體與圓柱體之間、立方體試塊間的抗壓強(qiáng)度轉(zhuǎn)化基本滿足該規(guī)律。而CECS 104:99在進(jìn)行標(biāo)準(zhǔn)立方體與棱柱體抗壓強(qiáng)度轉(zhuǎn)化計(jì)算結(jié)果方面，保證的是最小包絡(luò)線，即fcu,150對(duì)fc,150的轉(zhuǎn)化結(jié)果偏保守；尤其是C50以上的強(qiáng)度轉(zhuǎn)化規(guī)律呈現(xiàn)隨材料強(qiáng)度的提升轉(zhuǎn)化系數(shù)逐漸增加趨勢(shì)，這與工程實(shí)際情況存在差異，有必要進(jìn)行修正。針對(duì)C50以上的立方體和圓柱體實(shí)測數(shù)據(jù)進(jìn)行數(shù)據(jù)回歸分析，如圖5中虛線所示，依據(jù)轉(zhuǎn)化系數(shù)隨材料強(qiáng)度的變化趨勢(shì)，本文建議fcu,150與fcy,150的轉(zhuǎn)化方法采用下式計(jì)算：

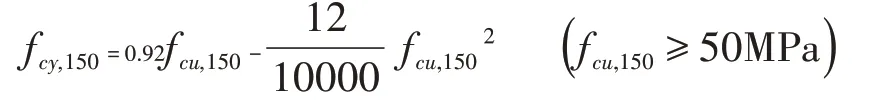
4 結(jié)束語

基于4種不同類型的混凝土試塊實(shí)測數(shù)據(jù)，本文分別對(duì)比分析了現(xiàn)行規(guī)范及學(xué)者提出的試塊強(qiáng)度轉(zhuǎn)化方法的精度和適用性，并提出了C50以上標(biāo)準(zhǔn)高強(qiáng)立方體試塊與對(duì)應(yīng)棱柱體試塊的抗壓強(qiáng)度轉(zhuǎn)化公式。

同時(shí)，分析了試塊尺寸、形狀等因素對(duì)強(qiáng)度指標(biāo)的尺寸效應(yīng)影響規(guī)律，具體如下：

（1）材料強(qiáng)度的提升及混凝土試塊體量的增加，均將引起試塊抗壓強(qiáng)度的衰減，其中試塊高寬比的增加造成抗壓強(qiáng)度衰減更明顯。

（2）《高強(qiáng)混凝土結(jié)構(gòu)技術(shù)規(guī)程》（CECS 104:99）規(guī)程和Peterson推薦方法分別在立方體試塊間抗壓強(qiáng)度轉(zhuǎn)換精度、標(biāo)準(zhǔn)立方體和棱柱體抗壓強(qiáng)度轉(zhuǎn)化精度上表現(xiàn)最佳。

（3）相比《混凝土結(jié)構(gòu)設(shè)計(jì)規(guī)范》（GB 50010-2002）和《高強(qiáng)混凝土結(jié)構(gòu)技術(shù)規(guī)程》（CECS 104:99）在標(biāo)準(zhǔn)立方體與棱柱體抗壓強(qiáng)度轉(zhuǎn)化精度和穩(wěn)定性上更佳，但兩者在高強(qiáng)材料的轉(zhuǎn)化精度上均有缺陷。