NSGA-II應(yīng)用于圓筒型永磁直線電機(jī)的多目標(biāo)優(yōu)化*
彭 珍,劉春元,饒章宇,李廣力
(1.浙江理工大學(xué)信息學(xué)院,浙江 杭州 310018;2.嘉興學(xué)院信息科學(xué)與工程學(xué)院)
0 引言
圓筒型永磁直線電機(jī)(TubularPermanent Magnet Linear Motor,TPMLM)具有推力密度高、伺服特性?xún)?yōu)良、加工裝配容易、氣隙磁場(chǎng)高且不存在橫向端部效應(yīng)等特點(diǎn),廣泛應(yīng)用于海浪發(fā)電[1]、振蕩系統(tǒng)[2]以及高精度數(shù)控機(jī)床[3]等工業(yè)領(lǐng)域,研究高效可靠的圓筒型永磁直線電機(jī)具有重要意義。
目前,電機(jī)優(yōu)化設(shè)計(jì)的主要目標(biāo)是提高推力密度[4],減少推力脈動(dòng)[5]等。近年來(lái),提出了很多相關(guān)的優(yōu)化方法,其中最為主要的優(yōu)化方法是結(jié)構(gòu)優(yōu)化[6]和算法優(yōu)化[7]。而其中的多目標(biāo)優(yōu)化是算法優(yōu)化中最為方便和高效的方法之一。
對(duì)于算法的優(yōu)化,文獻(xiàn)[8]為了防止算法“早熟”,提出了帶黑洞機(jī)制和混沌搜索的多目標(biāo)粒子群優(yōu)化算法,達(dá)到了增加種群的多樣性、提高算法尋優(yōu)精度的效果。文獻(xiàn)[9]為了同時(shí)實(shí)現(xiàn)新型軸向磁場(chǎng)永磁記憶電機(jī)的高性能和低成本,提出一種結(jié)合分層優(yōu)化策略的響應(yīng)曲面法(Response surface method,RSM)和基于罰函數(shù)與目標(biāo)約束的NSGA-II-M 多目標(biāo)優(yōu)化設(shè)計(jì)方法,并得出NSGA-II-M 在求解此類(lèi)多目標(biāo)優(yōu)化問(wèn)題上比RSM 更具優(yōu)勢(shì),同時(shí)也證明了NSGA-II 的有效性。因此,本文針對(duì)現(xiàn)有電機(jī)優(yōu)化中存在的優(yōu)化效率低、優(yōu)化效果不理想等問(wèn)題,提出使用基于NDX算子的NSGA-Ⅱ?qū)﹄姍C(jī)的功率和效率進(jìn)行多目標(biāo)優(yōu)化,以期實(shí)現(xiàn)電機(jī)的功率和效率的提升。
首先,搭建二維仿真模型,根據(jù)TPMLM 的尺寸在ANASYS Maxwell 上建立二維模型;其次,數(shù)據(jù)分析,計(jì)算優(yōu)化前電機(jī)的功率和效率,利用敏感參數(shù)分析法獲取主要影響變量;然后,多目標(biāo)優(yōu)化,利用基于NDX算子的NSGA-Ⅱ?qū)β屎托蔬M(jìn)行優(yōu)化,獲得Pareto前沿和優(yōu)化后的目標(biāo)值和變量值;最后再與優(yōu)化前的數(shù)據(jù)進(jìn)行對(duì)比,并使用樣機(jī)驗(yàn)證。
1 圓筒型永磁直線電機(jī)多目標(biāo)優(yōu)化模型
1.1 目標(biāo)函數(shù)
本文選取功率最大和效率最高作為電機(jī)設(shè)計(jì)的優(yōu)化指標(biāo),在TPMLM 電機(jī)的多目標(biāo)優(yōu)化敏感性?xún)?yōu)化分析中,目標(biāo)函數(shù)如式⑴、式⑵所示:

其中,Pout為電機(jī)的輸出功率,η為電機(jī)運(yùn)行時(shí)的輸出功率與輸出功率、磁滯損耗和繞組損耗之和的比值。輸出功率Pout和運(yùn)行效率η的計(jì)算如式⑶、式⑷所示:

其中,IA、IB、IC、UA、UB和UC為分別為內(nèi)部電路中三相電路各相電路的電流與電壓值;Pcore為磁滯損耗,磁滯損耗的數(shù)據(jù)由仿真模型導(dǎo)出;Pcu為繞組損耗,繞組損耗的計(jì)算如式⑸所示:

其中,R是三相電路上各相的繞組電阻,取阻值10Ω進(jìn)行計(jì)算。
1.2 優(yōu)化變量
本文所研究的TPMLM 的初始結(jié)構(gòu)參數(shù)數(shù)據(jù)如表1所示。
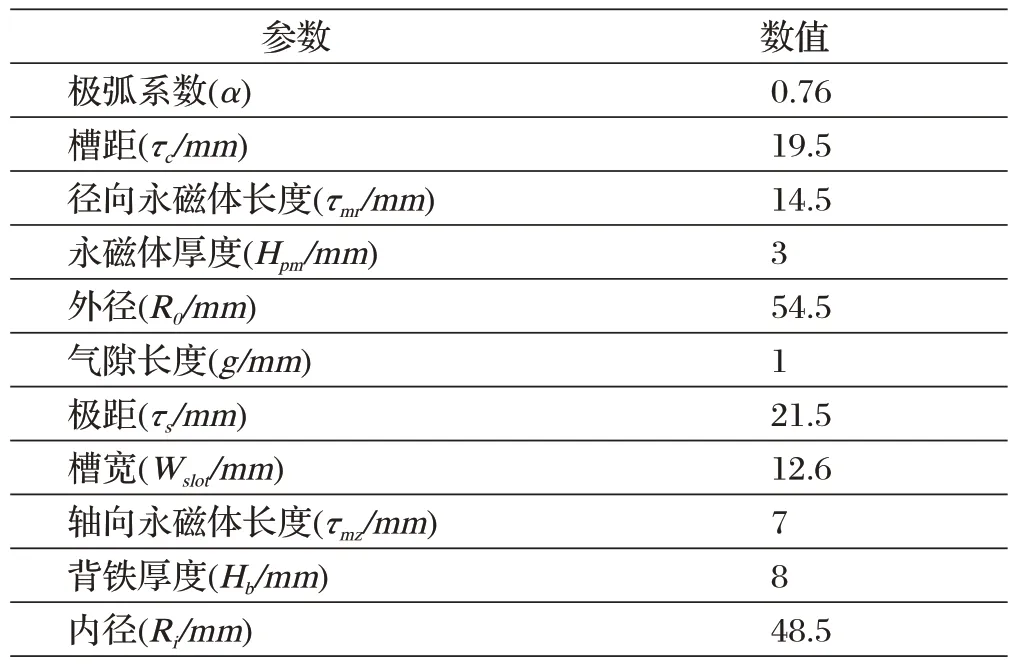
表1 電機(jī)設(shè)計(jì)主要參數(shù)數(shù)據(jù)
根據(jù)靈敏度分析[10],從表1 中的所有參數(shù)數(shù)據(jù)中選取了五個(gè)關(guān)鍵結(jié)構(gòu)參數(shù)作為T(mén)PMLM 的優(yōu)化變量。根據(jù)輸出性能隨參數(shù)變化進(jìn)一步給出每個(gè)參數(shù)變量的限制范圍,如表2所示。

表2 優(yōu)化變量及參數(shù)范圍
1.3 優(yōu)化設(shè)計(jì)流程圖
本文整體的優(yōu)化設(shè)計(jì)過(guò)程如下:首先,確定優(yōu)化目標(biāo)和設(shè)計(jì)變量以及變量的取值范圍。其次,計(jì)算和分析設(shè)計(jì)變量對(duì)優(yōu)化目標(biāo)的敏感性指數(shù),利用靈敏參數(shù)分析法選取靈敏度高的參數(shù)。然后,再利用基于NSGA-II的多目標(biāo)優(yōu)化算法生成優(yōu)化目標(biāo)的Pareto前沿。最后,確定設(shè)計(jì)變量的最佳值,通過(guò)仿真和實(shí)驗(yàn)驗(yàn)證電機(jī)的功率和效率的性能。具體如圖1所示。

圖1 多目標(biāo)優(yōu)化設(shè)計(jì)流程圖
2 基于NDX算子的NSGA-Ⅱ多目標(biāo)優(yōu)化
2.1 NSGA-II的特點(diǎn)
近年來(lái),多目標(biāo)優(yōu)化中采用了多種多目標(biāo)進(jìn)化算法,如多目標(biāo)粒子群優(yōu)化(MOPSO)、多目標(biāo)差分進(jìn)化(MODE)和多目標(biāo)遺傳算法(MOGA)。為了獲得具有最優(yōu)參數(shù)設(shè)計(jì)的良好優(yōu)化方法,在[11]中,對(duì)多目標(biāo)粒子群優(yōu)化算法(MOPSO)、多目標(biāo)差分進(jìn)化算法(MODE)和非支配排序遺傳算法(NSGA-Ⅱ)三種進(jìn)化算法進(jìn)行了性能評(píng)估。評(píng)估結(jié)果表明:MODE 存在過(guò)早收斂的問(wèn)題,而MOPSO 容易陷入局部最優(yōu)解,相比之下,MOGA 具有較強(qiáng)的全局搜索能力,但不能保證搜索的多樣性,收斂速度較慢,結(jié)果表明了NSGA-II提供了更好的最優(yōu)解,因此,本文使用NSGA-II 進(jìn)行多目標(biāo)優(yōu)化。
NSGA-Ⅱ由Deb[12]等人首次提出,其主要思想為帶有精英保留策略的快速非支配多目標(biāo)優(yōu)化算法,是一種基于Pareto 最優(yōu)解的多目標(biāo)優(yōu)化算法。NSGA-Ⅱ在執(zhí)行選擇、交叉和變異遺傳操作之前,會(huì)對(duì)個(gè)體先進(jìn)行分層排序,確定種群間的支配與非支配關(guān)系,同時(shí),提出個(gè)體的擁擠度和精英策略來(lái)保證種群的多樣性,并降低了計(jì)算復(fù)雜度并盡可能保留滿(mǎn)意解。
NSGA-II 的實(shí)數(shù)編碼所采用的交叉算子為模擬二進(jìn)制交叉(simulated binary crossover)算子,簡(jiǎn)稱(chēng)SBX 算子,定義為:對(duì)兩個(gè)父體x1和x2,按照以下方式生成兩個(gè)子個(gè)體c1和c2:

其中,β為隨機(jī)變量,在每一維上都需要重新生成,以第i維為例(設(shè)x1,i≥x2,i),可以將式⑹變換為如下形式:

(x1,i+x2,i)/2 表示兩個(gè)父體在第i 維上的中點(diǎn),將(x1,i-x2,i)/2視為該維上的搜索步長(zhǎng)。
基于SBX算子的NSGA-Ⅱ中的β為隨機(jī)變量,其搜索范圍有限,易出現(xiàn)局部最優(yōu)和進(jìn)化過(guò)程不穩(wěn)定等問(wèn)題。
2.2 基于NDX算子的NSGA-Ⅱ
針對(duì)SBX 算子的不足,將正態(tài)分布引入到交叉操作SBX中,即用1.481|N(0,1)|代替參數(shù)β來(lái)擴(kuò)大搜索空間,增強(qiáng)的空間搜索能力,N(0,1)為正態(tài)分布隨機(jī)變量。故式⑺可表示為:

基于NDX 算子的NSGA-Ⅱ在Pareto 前沿的完整性、均勻分布性、算法收斂性上都有顯著改善,更容易跳出局部最優(yōu),提高Pareto最優(yōu)解的質(zhì)量,并將此算法用于圓筒型永磁直線電機(jī)的多目標(biāo)優(yōu)化中,不僅能獲得更多具有代表性的非劣解,而且有利于其做出更合理的決策。改進(jìn)后的NSGA-II的流程圖如圖2所示。

圖2 NSGA-II流程圖
3 性能對(duì)比
所采用的基于NDX 算子的NSGA-Ⅱ的參數(shù)設(shè)置如下:種群規(guī)模大小設(shè)置為300;變異算子的變異概率設(shè)置為0.2;交叉算子的交叉概率設(shè)置為0.8;最大迭代次數(shù)設(shè)置為1000。優(yōu)化后的Pareto 前沿如圖3 所示,優(yōu)化前后設(shè)計(jì)變量的取值如表3所示。

表3 優(yōu)化前后的設(shè)計(jì)變量值

圖3 Pareto前沿
從圖3 可得:由于基于NDX 算子的NSGA-Ⅱ搜索空間更為廣闊,使得Pareto最優(yōu)解分布均勻,而且解的質(zhì)量要更高。通過(guò)優(yōu)化,功率由401.52W提高到了454.02W,效率從82.83%增大到了90.18%。
3.1 功率性能
在速度為0.5m/s,負(fù)載為10Ω時(shí)計(jì)算瞬時(shí)功率,優(yōu)化前后瞬時(shí)功率的結(jié)果如圖4所示,從圖中可以看出,優(yōu)化后的TPMLM的功率得到了增大,TPMLM的平均功率由優(yōu)化前的401.52W變?yōu)閮?yōu)化后的454.02W,達(dá)到了優(yōu)化效果。

圖4 功率的優(yōu)化結(jié)果
3.2 效率性能
TPMLM 的繞組的電阻取值為0.8Ω,在速度為0.1-1.0m/s時(shí)分別計(jì)算運(yùn)行效率,結(jié)果如圖5 所示,從圖中可以看出,優(yōu)化后的電機(jī)的工作效率相比優(yōu)化前,有明顯的提升,電機(jī)平均效率由優(yōu)化前的82.83%變?yōu)閮?yōu)化后的90.18%,達(dá)到了優(yōu)化效果。

圖5 效率優(yōu)化對(duì)比
4 實(shí)驗(yàn)
為了驗(yàn)證所設(shè)計(jì)的永磁直線電機(jī)能應(yīng)用于橋梁的減振系統(tǒng),使用MTS100kN 萬(wàn)能試驗(yàn)機(jī)模擬橋梁的振動(dòng)。實(shí)驗(yàn)平臺(tái)的搭建如圖6所示。

圖6 實(shí)驗(yàn)平臺(tái)
在電機(jī)的運(yùn)動(dòng)速度為0.112m/s,負(fù)載R=5Ω的工作條件下,用示波器測(cè)量感應(yīng)電動(dòng)勢(shì),用MTS100kN萬(wàn)能試驗(yàn)機(jī)讀取電磁力,即阻尼力。圖7(a)所示為測(cè)量的A相感應(yīng)電動(dòng)勢(shì),(b)為仿真的三相感應(yīng)電動(dòng)勢(shì)波形。從圖中可看出,其感應(yīng)電動(dòng)勢(shì)幅值測(cè)量值為15V,有限元計(jì)算值為15.4V,仿真計(jì)算值和實(shí)驗(yàn)測(cè)試值基本一致。
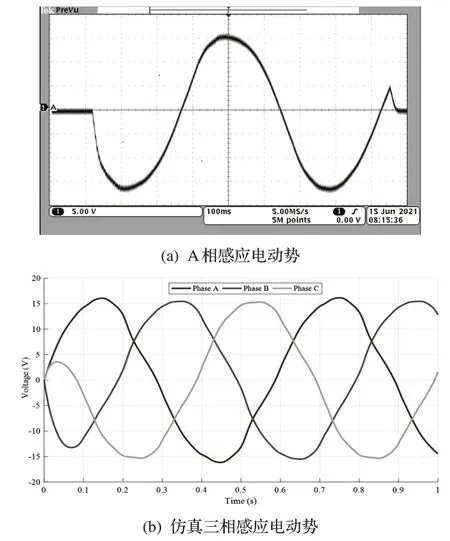
圖7 感應(yīng)電動(dòng)勢(shì)
5 結(jié)束語(yǔ)
本文提出了一種基于NDX 算子的NSGA-Ⅱ的TPMLM 的多目標(biāo)優(yōu)化設(shè)計(jì)方法。以效率和功率為優(yōu)化目標(biāo)。
本研究充分利用NSGA-II的全局收索能力對(duì)目標(biāo)進(jìn)行優(yōu)化,通過(guò)動(dòng)態(tài)擁擠度以及自適應(yīng)混合交叉算子保證解的多樣性,提高解的質(zhì)量;通過(guò)全局優(yōu)化,獲得電機(jī)結(jié)構(gòu)參數(shù)最優(yōu)解,實(shí)現(xiàn)TPMLM的最佳運(yùn)行性能。
樣機(jī)的仿真和試驗(yàn)結(jié)果表明:通過(guò)電機(jī)參數(shù)結(jié)構(gòu)的優(yōu)化,在不同狀況下,優(yōu)化后功率提高,效率提升,而且樣機(jī)實(shí)測(cè)表明該方法對(duì)TPMLM 結(jié)構(gòu)優(yōu)化設(shè)計(jì)的有效性。因此,所提出的TPMLM 優(yōu)化設(shè)計(jì)可以方便、高效地獲得最優(yōu)結(jié)構(gòu)設(shè)計(jì)。

