橋墩剛度對鐵路大跨連續梁橋車橋耦合振動的影響研究

周川江 徐昕宇 鄭曉龍 陳星宇

（中鐵二院工程集團有限責任公司， 成都 610031）

鐵路橋梁是構成高速鐵路的重要工程結構，必須具備足夠的剛度和良好的整體性，才能確保高速列車的運營安全性和乘坐舒適性。高速列車過橋時，力通過輪對經軌道作用到橋梁上，橋梁結構的整體剛度決定了橋梁的動力性能，進而對列車過橋的安全性和平穩性產生影響。

我國研究人員從20世紀80年代就開始了車橋動力耦合振動的理論和應用研究，至今已建立了多種動力分析模型，制定了相應的評價標準。翟婉明等［1］以簡支箱梁橋為研究對象，分析了橋墩橫向剛度對車 - 線 - 橋耦合系統動力性能的影響，結果表明橋墩橫向剛度不足將嚴重影響列車過橋時的安全性和平穩性，當橋梁梁體和橋墩的橫向剛度滿足規范要求時，影響列車安全性和平穩性的主要是行車速度和軌道不平順；夏禾等［2］以多跨簡支梁橋為研究對象，對車 - 梁 - 墩體系進行了動力相互作用分析，研究了橋墩振動對車輛運行安全性和平穩性的影響，并將仿真結果與實測結果進行了對比分析；寧曉駿等［3］以多跨簡支箱梁為研究對象，對高速鐵路橋墩的橫向剛度進行了研究，發現當簡支梁橋的墩高增加時，橋梁的豎向振動和車輛的動力響應變化均不大，但是橋梁的橫向響應變化較大；研究同時指出足夠的橋墩橫向剛度是高速列車運行的安全和平穩得以保證的重要因素；凌知民等［4］以混凝土連續梁橋為研究對象，分析了橋梁的動力響應，結果表明低墩和高墩的墩頂振幅相對較小，而中等高度橋墩由于橫向剛度相對較小，導致墩頂振幅較大。

已有研究的對象多為簡支梁橋或普通墩高連續梁，然而高速鐵路為了跨越江河、峽谷和既有線路，必須要設計一些大跨度特殊結構的橋梁。尤其是西部山區的高速鐵路，線路大多橫穿山嶺或溝谷，從而出現很多大跨連續梁橋。同時，由于山區地勢起伏較大，相鄰橋墩的墩高差異也可能較大，當橋梁的橋墩剛度、相鄰橋墩的高差改變時，可能會對橋上列車運行的安全性和平穩性產生不利的影響。然而，截至目前，相鄰橋墩高差的影響方面與影響程度究竟如何，業界尚無可借鑒的成熟經驗。

車橋耦合振動分析是列車和橋梁動力響應研究中最常用的方法。本文以某高墩大跨連續梁橋為研究背景，采用MSC Patran和ADAMS Rail軟件聯合動力仿真技術，對橋梁進行車橋系統耦合振動分析，研究橋墩橫向剛度和橋墩高差因素對車輛和橋梁動力響應的影響。

1 車 - 橋耦合振動模型

車橋耦合振動模型包含車輛子系統和橋梁子系統，子系統之間按照一定的輪軌運動關系耦合。鐵路車輛由若干節車輛單元組成，假設車輛單元之間是相互獨立的。每節車輛單元是由車體、轉向架、輪對及模擬懸掛結構的彈簧和阻尼元件組成的多自由度空間振動系統。車體和轉向架均考慮點頭振動、搖頭振動、沉浮振動、橫擺振動和側滾振動，輪對則考慮沉浮振動、橫擺振動和側滾振動。對于四軸車輛而言，單節列車的總自由度為27個。在車橋耦合系統中，依據真實尺寸建立橋梁有限元模型，主梁和橋墩按二節點空間梁單元建立，橋墩和主梁之間依據實際的約束狀況通過主從關系處理［5］。

建立車輛動力模型和橋梁動力模型后，以輪軌接觸處為界面，建立車橋耦合的輪軌幾何相容關系和相互作用力平衡關系。通過求解車輛和橋梁的運動方程，用迭代計算來滿足幾何相容和力的平衡條件。輪軌間采用赫茲接觸理論，考慮到輪對在鋼軌存在著蠕滑力，借助Kalker的滾動接觸簡化理論來計算蠕滑力［6］。

軌道不平順是使車輛產生振動的重要原因，是車橋耦合振動的主要激勵源之一［7-8］。我國高速鐵路總體技術條件中，建議采用德國高速線路不平順譜密度函數來進行列車平穩性分析。因此，選用德國高速鐵路低干擾譜模擬的軌道不平順作為激勵，該低干擾譜可適用于時速250 km以上的高速鐵路，可考慮高低不平順、方向不平順和水平不平順。德國低干譜轉換的軌道高低不平順樣本如圖1所示。

圖1 軌道高低不平順圖

2 工程概況

該高墩大跨鐵路橋為無砟軌道預應力混凝土連續剛構橋，梁體為單箱單室的變截面箱型梁，梁體全長352 m。箱梁頂板和底板寬度分別為12.6 m和7.8 m。全橋頂板厚62 cm，底板厚52 cm；底板在梁端梗肋處的厚度變化為52～120 cm；腹板厚度為50 cm，各支座附近腹板厚度的變化范圍是50～110 cm。梁體采用C55混凝土。橋梁跨度為（92 + 168 + 92） m。橋墩采用矩形空心墩，配1號邊墩，墩高32 m，墩頂橫向寬12 m，縱向寬5.2 m；2號主墩墩高95.5 m，墩頂橫向寬9 m，縱向寬10 m；3號主墩墩高100.5 m，墩頂橫向寬9 m，縱向寬10 m；4號邊墩墩高70 m；墩身變截面布置，墩頂橫向寬12 m，縱向寬6 m。橋梁總體布置如圖2所示。

圖2 橋梁總體布置圖（m）

采用有限元方法按實際尺寸建立橋梁分析模型。實測研究表明，混凝土橋阻尼比一般為2%～3%，本文模型阻尼比按2%選取。橋梁模型總共328個節點，322個單元。橋梁結構各振型的基頻如表1所示。

表1 橋梁自振頻率及振型表

車輛采用CRH3動車組，共8節列車編組，編組形式為M + T + 4×M + T + M，其中T代表拖車，M代表動車，車速分別為250 km／h、300 km／h、350 km／h、400 km／h。

列車過橋的安全性通常用脫軌系數、輪重減載率和輪軸橫向力來判斷，而舒適性通常用列車車體的橫向和豎向加速度來評判。TB 10621-2014《高速鐵路設計規范》對上述參數的規定如表2所示。

表2 列車安全性及舒適性評定指標及限值表

為研究橋墩剛度對車橋耦合系統動力響應的影響，開展不同橋墩橫向剛度和不同橋墩高差下的車橋耦合分析。橋墩橫向剛度的影響通過改變橋墩的橫截面特性來實現，橋墩高差的影響通過調整2號橋墩的高度來實現。

3 橋墩剛度對車橋系統動力響應的影響

3.1 橫向剛度影響

為充分研究橋墩橫向剛度較小時車橋系統動力響應的變化規律，橋墩設定大多為剛度不足時的情況。設定的橋墩橫向剛度與原剛度的比值分別為 0.05、0.1、0.2、0.4、0.6、0.8、1.0、1.2 和 1.4。各剛度比值下梁的一階橫彎和一階豎彎自振頻率如表3所示。

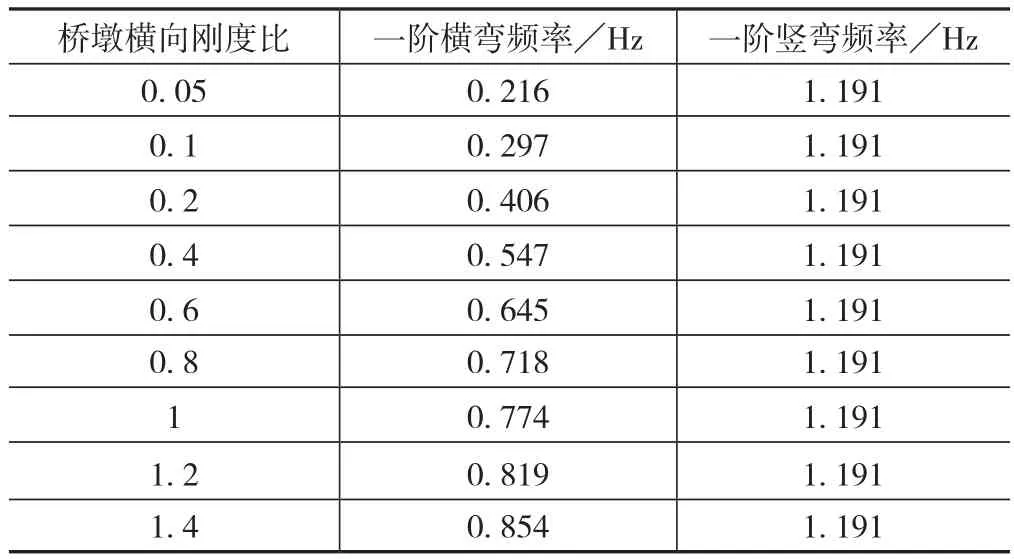
表3 不同剛度比值下橋梁的主要陣型頻率表

由表3可知，隨著橋墩橫向剛度的減小，橋梁的一階橫彎頻率逐漸減小，而一階豎彎頻率保持不變。

3.1.1 橋梁動力響應

橋梁主跨跨中橫向位移、主跨跨中豎向位移、梁端水平轉角和2號與3號橋墩墩頂橫向振幅隨橋墩橫向剛度和行車速度的變化情況如圖3所示。

由圖3可知，當橋墩橫向剛度逐漸減小時，橋梁主跨跨中橫向位移、梁端水平轉角、2號墩和3號墩的墩頂橫向振幅普遍增大。當橋墩橫向剛度在原有剛度的0.6～1.4倍范圍內變化時，橋梁的各橫向動力響應變化不大；但當橋墩的橫向剛度與原有橋墩剛度的比值小于0.6時，橋梁各橫向動力響應緩慢增大；當橋墩的橫向剛度與原有橋墩剛度的比值小于0.2時，橋梁的各橫向動力響應急劇增大；當橋墩橫向剛度與原有剛度的比值為0.4時，橋梁主跨跨中橫向位移與橋墩墩頂橫向位移比原來增加2倍多；如果橋墩橫向剛度與原有剛度的比值進一步減小至0.1倍時，橋梁主跨跨中橫向位移與橋墩墩頂橫向位移分別比原來增大6倍和10倍。400 km／h速度下，剛度比為0.1時，主跨撓跨比由原來的1／270 000增大至1／45 000。由此可知，橋梁主跨跨中橫向位移、梁端水平轉角、墩頂橫向位移對橋墩橫向剛度的變化比較敏感［9-10］。

由圖3（b）可知，橋梁豎向振動響應受橋墩橫向剛度變化的影響很小，橫向剛度的變化主要影響橋梁的橫向動力響應。表3中各剛度比值下，橋梁的一階豎彎頻率不變，也說明橋墩橫向剛度的減小對橋梁豎向振動的影響有限。

圖3 不同橋墩橫向剛度下的橋梁動力響應圖

250 km／h車速，剛度比為0.4、1.0和1.4時，橋梁主跨跨中橫向位移的時程曲線如圖4所示。隨著剛度比的減小，橋梁主跨跨中橫向位移在列車過橋過程中整體增大。

圖4 不同剛度比下主跨跨中橫向位移時程曲線圖

3.1.2 車輛動力響應

脫軌系數、輪軸橫向力、車體橫向加速度和車體豎向加速度隨橋墩橫向剛度和行車速度的變化情況如圖5所示。

圖5 不同橋墩橫向剛度下的車輛動力響應

由圖5和表2可知，總體上，在各橋墩橫向剛度比值與各行車速度下，車體的安全性和舒適性均滿足規范要求。橋墩橫向剛度的變化對脫軌系數、車輛輪軸橫向力、車體橫向及豎向加速度的影響不大，這可能是因為對大跨度橋梁而言，橋墩橫向剛度與原始剛度的比值在0.05～1.4范圍內變化時，橋墩橫向剛度的改變相當于長波不平順，因此對車輛的動力響應影響有限，此時行車速度和軌道不平順可能成為影響車輛動力響應的主要原因；當橋墩橫向剛度相同時，隨著行車速度的提高，車輛的脫軌系數、輪軸橫向力和車體豎向加速度均增大［11］。

250 km／h車速，橋墩橫向剛度與原始剛度的比值為0.4、1.0和1.4時，選擇第7節列車為研究對象，列車車體橫向加速度從進橋到出橋的時程曲線如圖6所示。從車體加速度時程曲線可以看出，在列車過橋的過程中，橋墩橫向剛度比的改變對車體橫向加速度產生的影響非常小。

圖6 不同剛度比下車體橫向加速度時程曲線

3.2 主墩高差的影響

該橋梁主墩為2號、3號橋墩，兩主墩原始高度分別為95.5 m和100.5 m，原始高差為5 m。為研究不同的主墩高差下車橋系統動力響應的變化規律，現通過減小2號墩的高度，來研究2號與3號墩高差分別為5 m、25 m、50 m、70 m時車橋系統響應的變化規律。不同主墩高差下，橋梁的一階橫彎和一階豎彎自振頻率如表4所示。

表4 不同主墩高差下橋梁的主要陣型頻率表

由表4可知，隨著2號墩高度的減小，兩主墩高差增大，橋梁的一階橫彎頻率逐漸增大，一階豎彎頻率變化不大。

3.2.1 橋梁動力響應

橋梁主跨跨中橫向位移、主跨跨中豎向位移、梁端水平轉角和橋墩墩頂橫向振幅隨主墩高差和行車速度的變化情況如圖7所示。

圖7 不同主墩高差下的橋梁動力響應圖

由圖7（a）和圖7（d）可知，各行車速度下，橋梁主跨跨中橫向位移和2號墩墩頂橫向振幅隨著兩主墩高差的增大而明顯的減小；由圖7（b）、圖7（c）、圖7（e）可知，主墩高差的增大對橋梁主跨跨中豎向位移、梁 端水平轉角和3號墩墩頂橫向振幅無明顯影響。

結合表4中橋梁的一階橫彎和豎彎變化規律可知，2號墩墩高的減小會增加2號墩和橋梁整體的橫向剛度，但對3號墩和橋梁豎向的整體剛度影響不大。通過減小2號墩的墩高來增大主墩高差的方式，會導致橋梁主跨橫向位移和2號墩墩頂橫向位移的減小，但是對橋梁主跨跨中豎向位移、梁端水平轉角和3號墩墩頂橫向位移不會產生太大的影響。

250 km／h車速，兩主墩高差為5 m、25 m、50 m和70 m時，橋梁主跨跨中橫向位移的時程曲線如圖8所示。隨著2號墩墩高的減小，兩主墩高差逐漸增大，橋梁主跨跨中橫向位移在列車過橋過程中整體減小。

圖8 不同主墩高差下主跨跨中橫向位移時程曲線圖

3.2.2 車輛動力響應

脫軌系數、輪軸橫向力、車體橫向加速度和車體豎向加速度隨主墩高差和行車速度的變化情況如圖9所示。

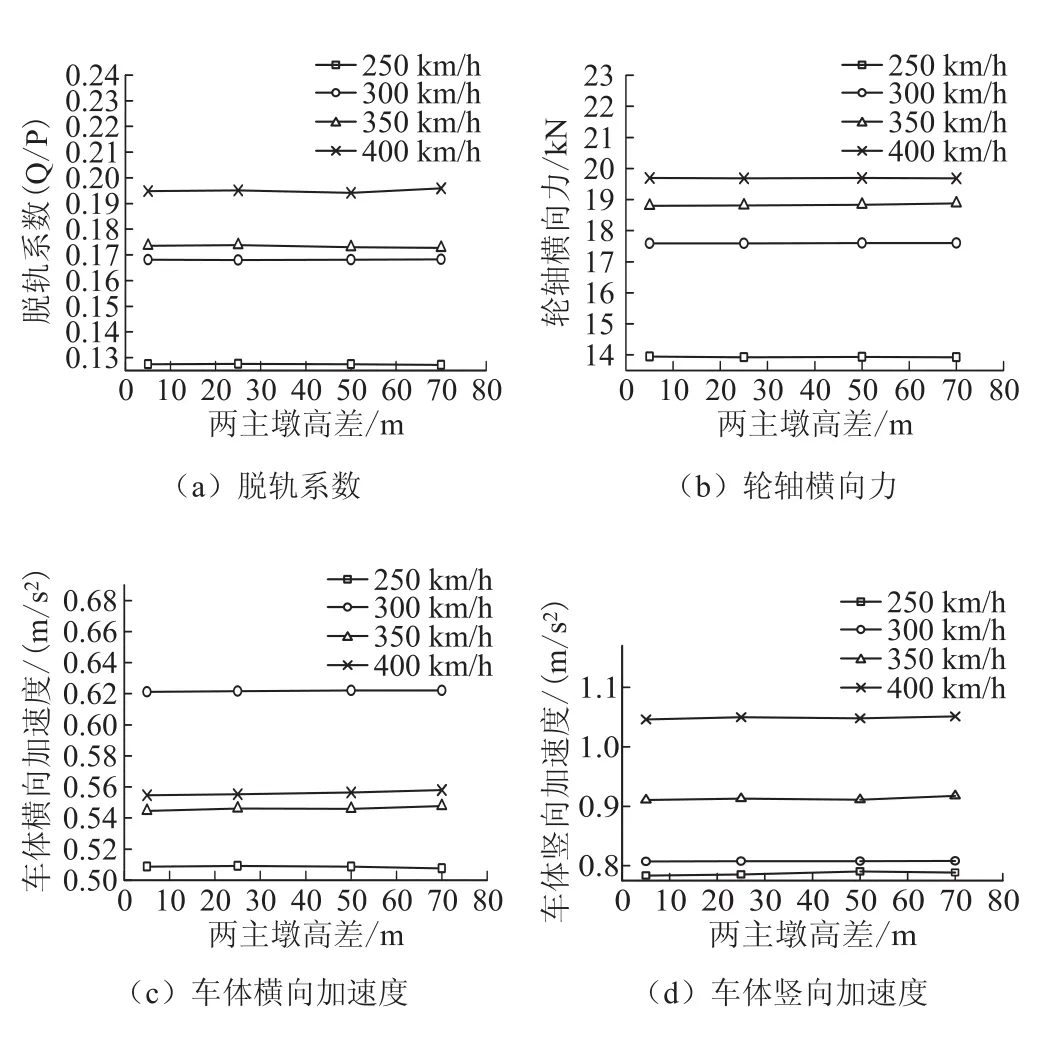
圖9 不同主墩高差下的車輛動力響應圖

由圖9和表2可知，總體上，在各主墩高差與各行車速度下，車體的安全性和舒適性均滿足規范要求。主墩高差對車輛脫軌系數、輪軸橫向力、車體橫向加速度和車體豎向加速度的影響不大，此時行車速度和軌道不平順可能成為影響車輛動力響應的主要原因。當主墩高差相同時，脫軌系數、輪軸橫向力和車體豎向加速度均隨行車速度的提高而增大。

250 km／h車速，主墩高差為50 m和70 m時，選擇第7節列車為研究對象，該節列車的車體橫向加速度從進橋到出橋的時程曲線如圖10所示。從車體加速度時程曲線可以看出，在列車過橋的過程中，主墩高差在5～70 m范圍內的改變對車體橫向加速度產生的影響非常小。

圖10 不同主墩高差下車體橫向加速度時程曲線圖

4 結論

本文以某高墩大跨鐵路橋梁為研究背景，研究了橋墩橫向剛度和橋墩高差對車輛和橋梁動力響應的影響，得出主要結論如下：

（1）橋墩橫向剛度的變化對高墩大跨連續梁橋的動力響應影響較大，隨著橋墩橫向剛度的減小，橋梁跨中和墩頂橫向位移的增幅急劇增大。

（2）在車橋耦合振動體系中，橋墩橫向剛度的變化對車輛的動力響應影響較小，這可能是因為對大跨度橋梁而言，橋墩橫向剛度的改變相當于長波不平順，因此對車輛的動力響應影響有限，此時行車速度和軌道不平順可能成為影響車輛動力響應的主要原因。

（3）通過減小橋墩高度來增大與相鄰橋墩的高差，將使該橋墩墩頂與橋梁跨中橫向位移明顯減小，但對其他橋墩以及橋梁豎向的動力響應影響不大； 橋墩高差的改變對列車的動力響應總體影響不大。