海上過駁卸載系統駁運任務規劃問題研究

劉寶新， 王宇哲

(陸軍軍事交通學院，天津 300161)

在戰爭及自然災害發生時，海上運輸有時會面臨港口碼頭被破壞的情況，為解決深吃水運輸船無法抵岸卸載的問題，可采用海上過駁卸載將裝備物資轉移上岸。海上過駁卸載是通過在具備一定水深的水域搭建過駁平臺，將運輸船上的裝備物資倒載至淺吃水的駁運船艇，再由駁運船艇將裝備物資轉移至岸灘的方式。海上過駁卸載環境適應性較強，但作業環節多，作業節點之間相互影響。卸載系統類似于一個物資轉運中轉站，裝備物資的中轉依靠駁運船艇的往來駁運，由于倒載的裝備物資類型不同，駁運船艇裝載能力不同，駁運任務規劃是否科學合理，對于海上過駁系統整體運行效率高低有著重要影響。本文充分分析海上過駁卸載作業流程，以整體作業時間最短為目標，提出規劃駁運任務方法，為部隊實踐提供參考。

1 海上過駁卸載系統作業過程

海上過駁卸載大體可分為3個環節：海上過駁、近岸駁運和岸邊卸載。海上過駁是通過特定的過駁平臺，為深吃水運輸船提供臨時靠泊的泊位，以滾裝或吊裝的方式，將裝備由運輸船上卸下，并裝載至淺吃水的駁運船艇上；近岸駁運是駁運船艇在裝載裝備物資后，利用駁運船艇可直接抵灘的能力，在過駁平臺和岸邊來回往復倒載物資的過程；岸邊卸載是在海灘等自然環境地形下將裝備物資由駁運船艇上卸下的過程，3個環節相互銜接，相互影響。

2 海上過駁卸載系統駁運任務規劃

2.1 海上過駁卸載系統優化目的

海上過駁卸載系統的優化目的，根據任務性質、任務目標有所不同。美軍在聯合海岸后勤行動中常使用的JOTE模型，是探究多個卸載子系統下的駁運船艇資源分配問題，該模型的優化目標是使得整個系統中待轉運物資總量最少，即所有卸載通道中裝備物資總量與駁運船艇駁運裝備物資總量之差最少[1]，是追求卸載需求與卸載能力之差最小化的模型，可使各卸載子通道的卸載能力相對均衡，有利于提升海上過駁卸載的持續性和經濟性。在實踐中，對于具體某一過駁卸載，各級指揮員常常關注的問題是，如何利用現有駁運船艇資源，在最短時間內完成卸載，研究該問題對于指導實踐有著重要意義。

2.2 以最短用時為目標的駁運任務規劃

海上過駁卸載系統作業環節多且相互銜接，要求各作業環節效率相互匹配，影響卸載能力的因素較多，其中近岸駁運次數多，涉及不同類型的裝備物資和駁運船艇，任務需求和保障能力不能統一衡量計算，是運籌學中多任務指派、資源配置的問題。

海上過駁任務完成的標志是最后1臺裝備上岸，假定某海上過駁系統運行順暢、各作業環節的銜接不會出現等待擁堵等情況，則卸載任務完成時間是最后一艘次駁運船艇完成最后一次駁運任務的時刻。

對于駁運船艇，每一次駁運任務及其所用時間主要有：靠泊平臺，時間T1;裝載裝備，時間TL;離開平臺，時間T2;近岸駁運，時間T3；抵灘，時間T4；卸載裝備，時間TU；退灘，時間T5；返回平臺，時間T6。

八項作業中，T1、T2主要與駁運船艇類型、過駁平臺類型有關，T3、T6與駁運船艇類型和駁運距離有關，T4、T5與駁運船艇類型有關，故當過駁平臺類型、離岸距離確定時，在卸載系統資源配置協調情況下，各類型駁運船艇每次駁運任務的T1～T6時間也相對固定，將T1～T6共6項相對固定時間之和稱為航行時間TH。

對于裝備裝載時間TL和卸載時間TU，則與裝備類型、駁運船艇類型、裝備數量、裝卸載方式等有關。駁運船艇的裝載能力主要受空間大小、載重的限制，不同類型的裝備裝載數量也不同，應當有所區分。以裝備的尺寸、重量為依據，結合駁運船艇的裝載能力，假設將裝備類型劃分為4類。各類型駁運船艇裝載不同類型裝備的最大裝載數量如表1所示，考慮到為了增加駁運船艇駁運效率，一次駁運任務可裝載多種類型的裝備，若窮舉出所有可能的組合，則會消耗大量計算時間。為簡化運算，本文提出裝備裝載系數的概念，即同類型裝備最大裝載數量的倒數，當每次駁運搭載裝備的裝載系數之和不大于1，即認為能夠裝載。例：對于A型駁運船艇，1臺類型1裝備的裝載系數是0.5、1臺類型3裝備的裝載系數是0.25，1臺類型4裝備的裝載系數是0.25,三者裝備系數之和等于1，即可同時裝載于A型駁運船艇上。

海上過駁作業，通常是通過搭接跳板連接過駁平臺與駁運船艇，裝備滾裝通行上艇，速度較快；但由于不同類型的駁運船艇，其結構型式、艙門大小、空間大小等有所不同，裝備裝卸載的時間不可同一而論，應當區別計算。在裝載時，裝備駛入駁運船艇指定位置后，捆綁加固工作隨即展開，在最后一臺裝備駛入船艇時，前序裝備的捆綁加固通常也已完成，模型不再單獨考慮裝備的捆綁加固時間。根據相關實踐數據統計，不同駁運船艇裝卸載單臺不同類型裝備的時間如表2所示。

表1 各類型駁運船艇裝載不同裝備能力

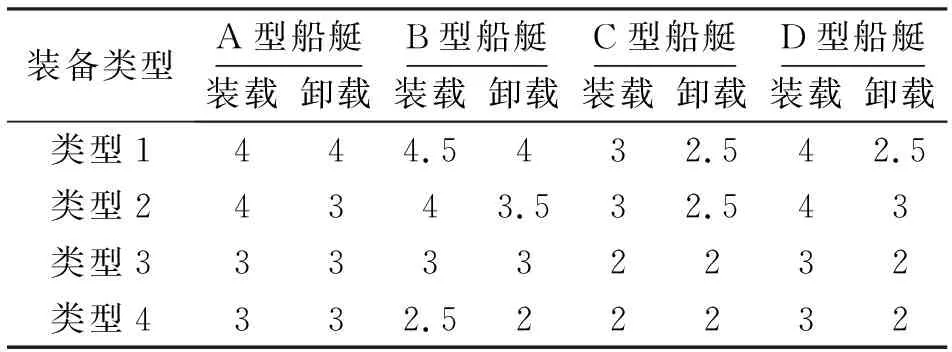
表2 各類型駁運船艇裝載單臺不同裝備時間 min

結合表2內容，TL、TU可用駁運船艇所運載的裝備數量表示。TH則是各型駁運船艇單次駁運時間與駁運次數之積，駁運次數可用所運裝備的裝載系數之和表示(向上取整)。單艘駁運船艇總作業時長，即是所有駁運次數中TH、TL、TU之和。海上過駁系統駁運的最短時間，即是所有駁運船艇的最大單艘作業時間，故系統最短作業時間的目標函數可以表示為：

?i

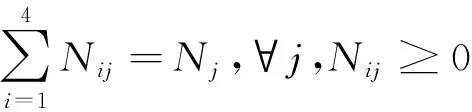
式中：i為駁運船艇類型；j為裝備物資類型;Ni為i型的駁運船艇的數量；Nj為需要駁運的j型裝備數量；Nij為i型的駁運船艇倒運裝備j的總數量；TLij為單個j型裝備裝載到i型船艇的時間；TUij為單個j型裝備從i型船艇卸載的時間；Pij為單個j型裝備裝載對應i型船艇的裝載系數。

3 模型應用

3.1 任務背景

以某海上過駁卸載系統做模型應用研究，相關數據已做模糊處理。已知海上過駁平臺搭設在離岸3海里處，有A、B、C、D共4種類型的駁運船艇可供使用，其數量分別為3、3、2、1艘。四種類型駁運船艇的航行時間TH如表3所示。

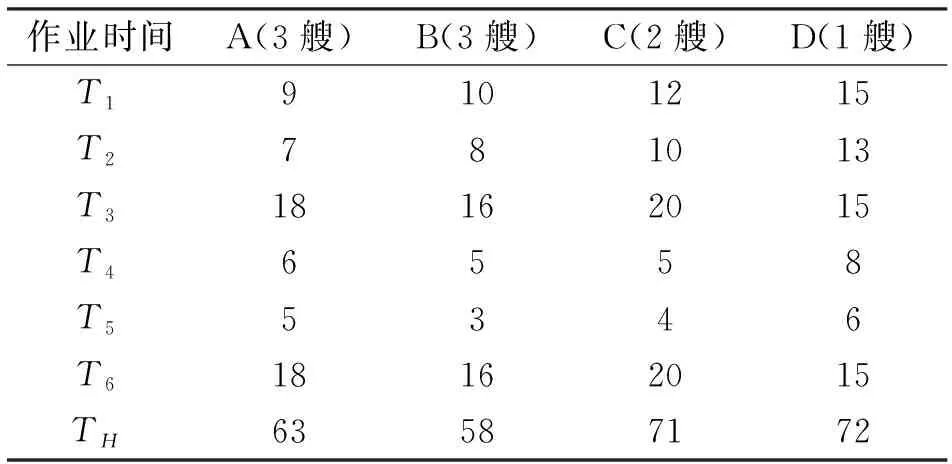
表3 各類型駁運船艇航行時間min

所需駁運的各類裝備數量如表4所示，由4艘滾裝運輸船搭載，不考慮運輸船停泊、靠泊之間的空檔期。

表4 卸載任務需求 臺

3.2 模型求解

將相關任務參數代入到模型之中，該模型為混合整數非線性規劃問題，可利用LINGO軟件求解，程序代碼為：

model:

sets:

boat/1,2,3,4/:travel,num,time;

cargo/1,2,3,4/:task;

link(cargo,boat):x,per,load,unload;

endsets

data:

num=3,3,2,1;

travel=63,58,71,72;

task=100,100,200,300;

load=2.5,4.5,3,4,2,4,3,4,1.8,3,2,3,1.2,2.5,2,3;

unload=2,4,2.5,2.5,1.8,3.5,2.5,3,1.5,3,1,2,1,2,1,2;

per=0.5,0.5,0.25,0.25,0.5,0.25,0.25,0.25,0.25,0.166,0.167,0.125,0.25,

0.125,0.166,0.125;

enddata

@for(boat(j):time(j)=(@sum(cargo(i):x(i,j)*per(i,j)*travel(j))+

@sum(cargo(i):x(i,j)*load(i,j))+@sum(cargo(i):x(i,j)*unload(i,j)))

/num(j));

[obj]min=@smax(time(1),time(2),time(3),time(4));

@for(cargo(i):@sum(boat(j):x(i,j))=task(i););

@for(link:@gin(x));

end

3.3 求解結果

求解得駁運任務最短耗時為1 393.5 min，任務分配結果如表5，各型駁運船艇的具體作業參數如表6所示，作業時間較為均衡。在戰時海上運輸投送中，裝載通常在我方港口進行，準備時間相對充分，作業環境相對穩定。而卸載在對方海域展開，海上過駁卸載面臨復雜自然環境、敵情威脅等諸多不利因素干擾，但作戰行動又要求裝備物資能快速上陸，迅速、持續形成戰斗力。因此，卸載往往比裝載難度大，也要求具有更高的時效性，在制定裝載方案時就應當考慮如何“卸得快”，即“裝載服務于卸載”。模型求得的駁運任務，也可以給制定裝載方案提供參考。

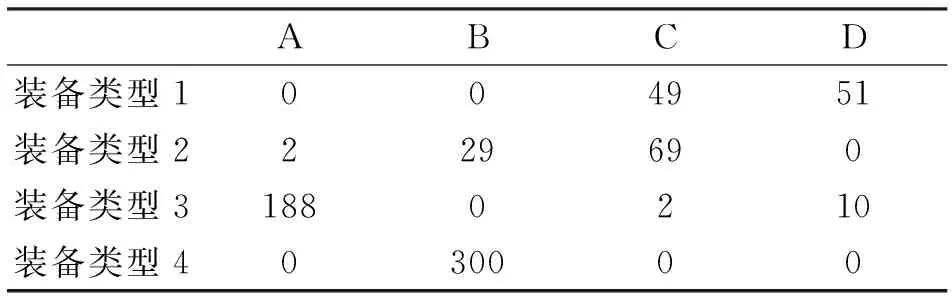
表5 各型駁運船艇駁運不同裝備物資數量 臺

表6 各型駁運船艇駁運參數

4 結束語

在分析海上過駁卸載作業流程的基礎上，提出不同類型駁運船艇應當區別考慮作業時間，提出利用裝載系數以簡化計算的方法，通過LINGO求解如何利用現有駁運船艇資源，實現最快速的卸載，一定程度上減少海上過駁卸載中駁運的盲目性，為科學高效規劃駁運任務提供一種方法，可幫助指揮機構估算駁運時間和制定卸載方案，為部隊實踐提供參考。但本文只考慮了海上過駁卸載系統運行流暢、各作業環節之間銜接不需要等待的情況，而在實踐過程中，常常會在駁運船艇靠泊過駁平臺、抵灘作業時產生排隊作業情況，今后的研究中還需綜合考慮等待時長等因素的影響，使計算結果更好的服務于應用。