基于加權分位數回歸參數估計的AR模型及其應用

劉 碩， 王江榮

(蘭州石化職業技術大學信息處理與控制工程學院，甘肅 蘭州 730060)

高速公路路基邊坡存在施工期和工后運營期邊坡變形控制問題，解決該問題的關鍵在于能及時準確地預測出公路路基邊坡的水平位移和豎直位移(或沉降量)。科學監測并以監測所得時間序列為基礎，構建高精度預測模型是解決此類問題的保障。受監測條件(水文地質、周邊環境、氣溫、降雨、監測儀器精度等)影響，監測時間序列往往具有非線性、非平穩性、相依性和相關性等特點，選擇理想的數學模型(用以表述此類序列)和模型參數估計方法就顯得尤為重要。ARIMA模型(Auto-Regression Integrated Moving Average)對非平穩序列有較好的適用性，因此本文選用該模型來擬合預測這類時間序列。ARIMA模型與回歸分析模型、灰色理論模型、組合模型和統計模型[1-4]類似，都是建立在各次觀測相互獨立、觀測誤差數學期望為零、方差相等且隨機誤差呈正態分布這些假設基礎上的。但實際觀測數據往往出現波動性大、呈異方差現象，難以滿足這些假設條件，在這種情況下如果采用最小二乘回歸法估算模型參數會造成模型穩健性變差、預測誤差偏大，從而失去對工程實踐的指導性。若采用分位數回歸估算模型參數，則對模型隨機誤差分布不做任何假設(或不做任何要求)，而且分位數回歸估參還具有高精度、高效率及穩健性強等特點[5-7]，克服了傳統最小二乘估計的缺陷(要求隨機誤差項滿足齊方差正態同分布)。其次，為了提升分位數回歸的穩健性，消除預測模型厚尾誤差對模型參數估值的影響，可通過對觀測序列中的異常值賦予較小的權值以削弱其對分位數回歸參數估值的影響(或干擾)；而對正常觀測值或優質觀測值則賦予較大的權值以突出其估值的作用和地位[8-9]。相對于非線性估參的MA、ARMA及ARIMA等模型，AR模型是線性估參，該模型估值更容易且參數意義便于解釋，故在實際建模時可用高階AR模型替換ARIMA模型[10]。實證分析也表明加權分位數回歸參數估計的AR(p)模型具有較高的預測精度，優于其他一些預測模型。

1 加權分位數自回歸AR(p)模型

由Koenker等人于1978年提出的分位數回歸模型參數估計是一種全面數據統計分析方法[11]，是對傳統最小二乘法的發展，具有很強的穩健性和抗干擾能力(不易受監測數據列中異常點的影響)，且對時間序列模型的隨機誤差項無任何要求。該方法最大的優勢在于能夠保留變量之間的大部分信息，同時還能夠較好地解決異方差問題，使所建模型更具魯棒性[12]。

設路基邊坡變形監測時間序列Yt(t=1,2,…,n)的p階自回歸AR(p)模型為：

Yt=θ1Yt-1+θ2Yt-2+…+θpYt-p+ζt,

(t=p+1,3,…,n)

(1)

式中:θ=[θ1,θ2,…,θp]為模型參數;ζt為模型隨機誤差項。

設FYt|(Yt-1,Yt-2,…,Yt-p)(y)(t≥p+1)是建立在隨機變量(Yt-1,Yt-2,…,Yt-p)基礎上Yt的條件分布函數，則Yt在分位點τ∈(0,1)的條件分位數為

Qτ(Yt|Yt-1,Yt-2,…,Yt-p)=

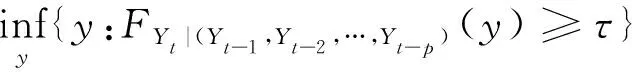
(2)

其中inf(·)是下確界函數。

顯然，在(Yt-1,Yt-2,…,Yt-p)(t≥p+1)條件下，Yt在分位點τ的條件分位數為Yt-1,Yt-2,…,Yt-p的線性函數，即Qτ(Yt|Yt-1,Yt-2,…,Yt-p)=θ1Yt-1+θ2Yt-2+…+θpYt-p，則參數向量θ(τ)在分位點τ的分位數估計值為

(θ1Yt-1+θ2Yt-2+…+θpYt-p))

(3)

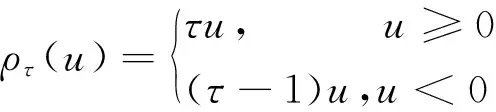
另外，式(3)等價于下面的式(4)，即

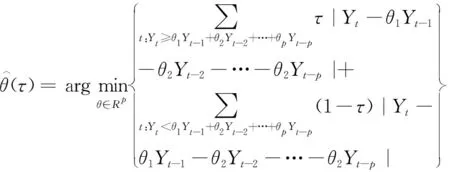
(4)

顯然，隨著分位點τ的改變，分位數回歸所估算出的模型參數也會不同，因而可求得不同自回歸AR(p)方程(傳統回歸法只能得到一個回歸方程，會造成數據信息丟失)，從而使路基邊坡監測數據中的大部分有用信息能夠被提取出來，增加了模型預測結果的可靠性和可信度。

為了進一步加強和提升分位數回歸的穩健性，削弱AR(p)模型厚尾誤差對模型估參的影響，本文通過給損失函數賦權(即對觀測異常點賦予較小的權值，而對正常點或優質點則賦予較大的權值)使所估算出的模型參數更加貼近理想值，從而提高模型的預測精度。

對式(3)中損失函數加權后得到AR(p)模型位于分位點τ的參數估計值為

(θ1Yt-1+θ2Yt-2+…+θpYt-p))

(5)

式(5)中權函數ωt為[13]：

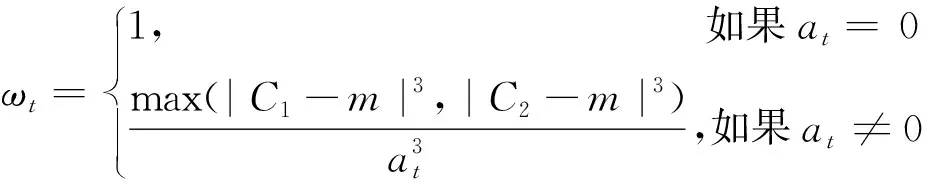
(6)

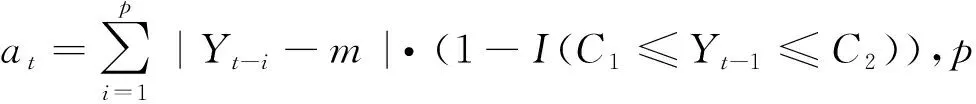
2 工程實例分析

2.1 數據來源及模型選定

數據來自于重慶奉云高速公路K1360+500-+660段，位于滑坡中部ZK2-3附近JC1-6監測點的累計水平位移，工程概況詳見文獻[14]。表1給出了2015年3月21日至2015年11月23日，所完成的37期監測數據。在37期的累計水平位移序列中，取前33前期樣本數據用于建模，后4期樣本數據用于檢驗模型的準確性。按表1中數據繪制累計水平位移時序圖，繪制結果如圖1所示。

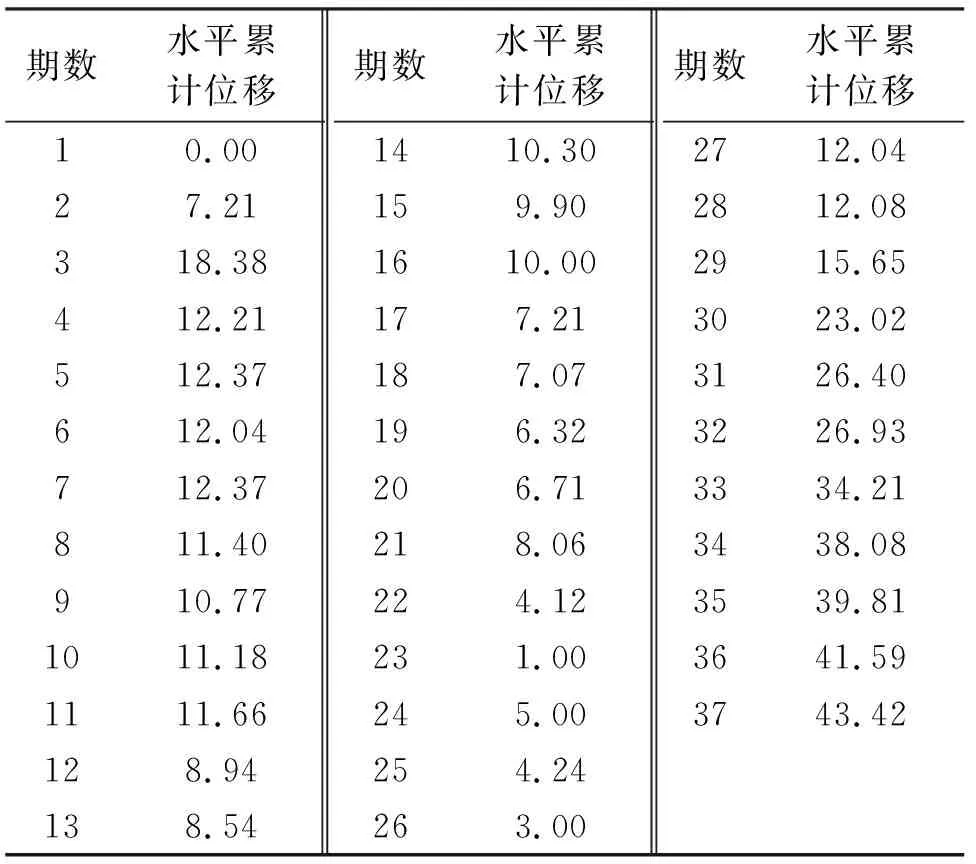
表1 JC1-6監測點的水平位移 mm

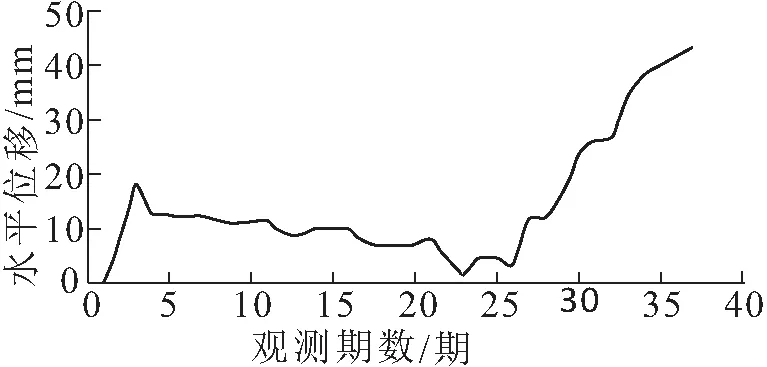
圖1 監測點JC1-6的累計水平位移

從圖1可看出，受周邊工程開挖、水文氣象條件等因素影響，監測出的累計水平位移時間序列出現了較大的波動性，呈現出明顯的非線性和非平穩性，適合用ARIMA模型表征描述。另外，在利用EViews軟件對表1中時間序列進行自相關(ACF)及偏自相關(PACF)分析時發現自相關具有拖尾性，而偏自相關具有階截尾性，因此可用AR(p)模型擬合預測此時間序列。分別計算AR(1)、AR(2)、AR(3)、AR(4)、AR(5)、……的AIC值(Akaike Information Criterion，赤池信息準則法)，得到的結果分別為5.721 6、5.741 2、5.791 8、5.608 4、5.653 8、5.707 6、5.761 6……，并以最小的AIC值所對應的模型為選定模型[15]。最終選定AR(4)為本例分析模型。

2.2 分位數回歸建模及預測分析

設時間序列模型AR(4):Yt=θ1Yt-1+θ2Yt-2+θ3Yt-3+θ4Yt-4+ζt，選用5個不同分位點τ=[0.1,0.3,0.5,0.7,0.9]進行討論；結合分位數回歸與遺傳算法，估算模型參數θ=[θ1,θ2,θ3,θ4]。按式(5)定義適應度函數(即目標函數)：

(θ1Yt-1+θ2Yt-2+θ3Yt-3+θ4Yt-4))

(7)

式(7)中Yt(t=1,2,…,32,33)來自表1中前33期的監測數據(即建模樣本數據)。

利用MATLAB編寫適應度函數程序(函數名記為finess.m，具體程序在此略去)，在計算權函數ωt時，可用MATLAB自帶函數prctile確定C1和C2(本例經試算k=25最優，即需計算25%和75%的分位數值)；模型參數的搜索范圍為[-1.5,1.5]。當權函數ωt≡1(t=1,2,3,…)時，由式(7)得到的參數值為非加權分位數回歸估值，結果見表2。

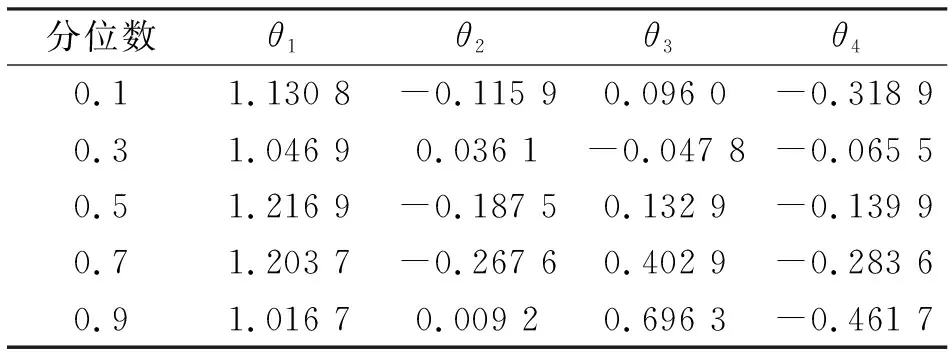
表2 非加權不同分位點AR(4)模型參數估計值

將表2中各組參數值代入式(1)，并用得到的AR(4)模型對表1中后4期數(即34～37)的監測值進行預測和分析，結果見表3和表4。

從表3和表4可看出，在非加權條件下，AR(4)在不同分位數的預測結果及精度各不同，其中以分位數0.5得出的AR(4)預測效果最優(預測值整體

表3 非加權不同分位點AR(4)水平位移預測值 mm

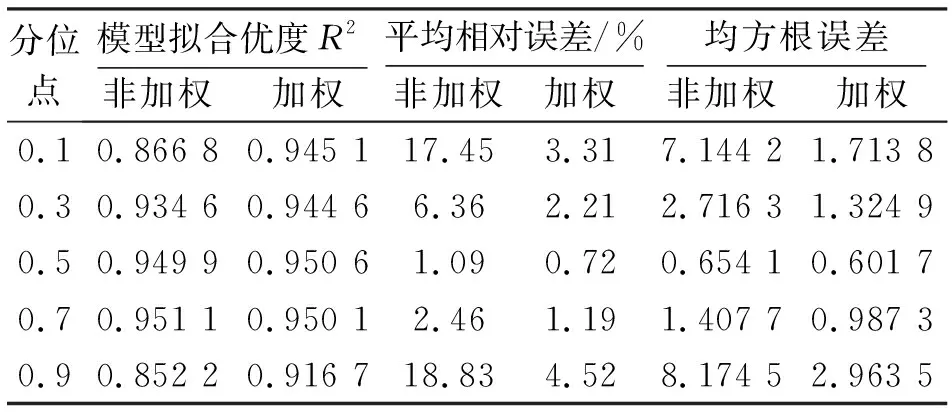
表4 加權和非加權AR(4)水平位移預測精度

更接近實測值，即平均精度更高)。接下來再給出加權條件下，模型參數估計值及所得模型對表1后4期水平位移的預測值，分別見表4～表6。

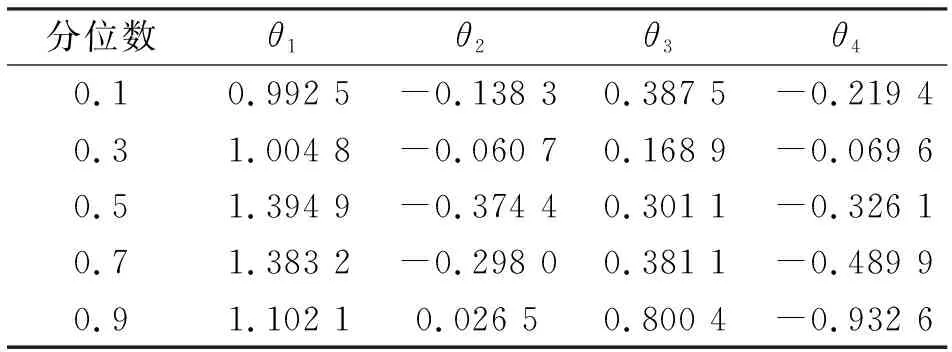
表5 加權不同分位點下AR(4)模型參數估計值

表6 加權不同分位點AR(4)水平位移預測值 mm

從表4～表6可以看出，加權分位數回歸估值，按各分位點(τ=0.1、0.3、0.5、0.7、0.9)得到的AR(4)模型預測精度均有了較大提高，整體優勢明顯。以上結果表明，引入權函數ωt對提高模型的擬合預測精度發揮了重要作用：抑制了隨機誤差異方差性對模型精度的影響，使估算出的模型參數值更接近理想值。值得注意的是，在加權條件下，各分位數自回歸AR(4)模型的擬合優度值均大于0.9，說明得出的擬合預測值具有較高的可信度，可根據實際工程對精度要求，靈活選擇所需模型。本文選擇τ=0.5對應的加權分位數自回歸模型(見式(8)，為本例最終模型)與其他模型(式(9)～式(10))進行對比分析。

yt=1.394 9yt-1-0.374 4yt-2+

0.301 1yt-3-0.326 1yt-4(t=5,6,7…)

(8)

基于最小二乘參數估計的AR(4)模型為：

yt=1.171 9yt-1-0.095 9yt-2+

0.296 7yt-3-0.342 4yt-4(t=5,6,7…)

(9)

一階差自回歸移動平均ARIMA(2,1,2)(借助AIC信息準則識別法確定)模型：

yt=13.051 16+1.885 423yt-1-0.912 305yt-2+

ζt+0.969 266ζt-1-0.288 398ζt-2(t=3,4,5…)

(10)

不同模型的預測結果及精度分析見表7、表8。

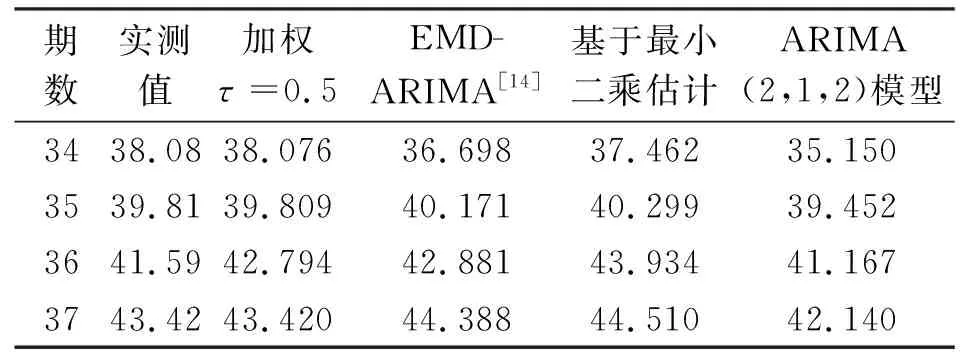
表7 不同模型的預測結果及比較 mm

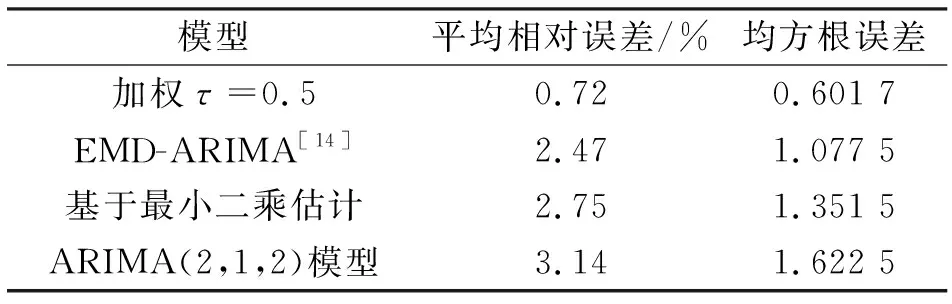
表8 不同模型的預測精度

根據四種模型的預測結果及預測精度來看，本文模型(式(8))具有明顯優勢，預測效果遠好于其他三種模型。當模型隨機誤差項存在異方差性時，用最小二乘法(要求模型隨機誤差項具有同方差、同分布且誤差均值為0)估算出的模型參數偏離了理想值，即最小二乘估計對含異常點的數據列適應能力也較差，進而影響了模型的預測精度；建立在“LS-Least Squares(NLS and ARMA)”參數估算的AMIMA模型同樣存在這樣的問題；分位數回歸則具有很強的數據適應能力，同時對模型隨機誤差項不做任何要求和假設(對建模數據的平穩性要求不高)，因此具有很強的穩健性和抗干擾能力。另外，隨著權函數的引入使分位回歸估算出的參數值更接近理想值，從而增強了模型的穩健性，提升了模型的預測精度。更重要的是，本文模型除了精度較高外，還具有結構簡單、使用方便的特點，便于工程技術人員借鑒。

3 結束語

加權分位數回歸拓展了時間序列模型AR(p)參數估值方法，可按不同分位點估出多組參數值，使得模型在土木工程變形預測時有更多選擇，可按施工期和工后使用期靈活選用。由于權函數僅受監測數據列的驅動，對模型殘差具有調節作用，因此可有效抑制異常數據點對模型參數估值的干擾，進而增強分位數回歸參數估值和所得模型的穩健性。分位數回歸對模型的隨機誤差項統計特性無任何要求，具有很強的數據適應能力，要優于最小二乘估計。工程實例分析表明，基于加權分位數回歸參數估值的自回歸AR(p)模型具有很高的預測能力(外推能力)，用于工程實踐完全可行。另外，對于非等間隔時間序列，可先等間隔化后再按本文方法建模；對非平穩非線性時間序列采用高階自回歸AR(p)作為預測模型同樣完全可行，進一步拓寬了本文分位回歸建模方法的使用范圍。