線性自抗擾控制器的改進設計及應用

張 永， 王 佑， 薛亞麗,3， 李 政,3

(1.國能蚌埠發電有限公司，安徽蚌埠 233411； 2.清華大學 能源與動力工程系，電力系統及發電設備控制和仿真國家重點實驗室，北京 100084； 3.清華大學 山西清潔能源研究院，太原 030006)

以火電機組為代表的熱力過程普遍存在高階大慣性系統動態的特點，常規的比例-積分-微分(PID)控制的效果有待提升。隨著智能技術的發展，許多學者針對熱力過程控制提出了較先進的控制方法。Uddin等[1]基于智能算法設計了神經網絡非線性控制結構,并將其應用于鍋爐主汽壓力控制；陸穎等[2]基于強化學習方法對過熱汽溫串級控制器進行在線參數整定和優化；Zhang等[3]基于Ⅱ階Renyi熵準則和神經網絡對串級過熱汽溫系統的外環PID進行訓練。但是上述控制系統設計較為復雜，在線計算量較大，較難被應用于分散控制系統中。

由于線性自抗擾控制(ADRC)具有結構簡單、整定方便、魯棒性好及易于現場實現等優點，近年來得到了深入的研究和廣泛的應用[4-5]。但對于大慣性大時滯過程，ADRC的快速性不盡人意。為此，有學者提出了不同的改進方法，如文獻[6]～文獻[8]分別提出了帶時滯補償的自抗擾控制和采用史密斯預估器進行補償的自抗擾控制，改善了ADRC對高階時滯對象的控制效果，但仍存在控制量波動較大等問題，一定程度上限制了其在工程上的實際應用。

對于存在高階慣性或時滯的系統，由于系統輸出與輸入間的滯后關系，無法將常規反饋控制閉環動態響應設計得過快，否則易產生超調；相比之下，由于系統開環階躍響應的控制動作可一步到位，無需反復調整，可近似表征系統在反饋控制下閉環能夠達到的較快響應過程，因此對于大慣性過程，筆者以被控過程的開環階躍響應作為預期動態，設計閉環控制系統。

為提高擴張狀態觀測器(ESO)對大慣性系統的觀測效果，可以考慮設計補償環節，使得被控對象在ESO觀測中近似為比例環節，從而使得閉環動態性能與預期動態一致。筆者提出了一種基于模型補償的自抗擾控制器設計方法，并給出了其參數整定的公式，為該控制器的工程應用提供了參考。

1 自抗擾控制器的改進設計

1.1 線性自抗擾控制原理

筆者在Ⅰ階線性自抗擾控制器的基礎上進行改進設計。為此，可用如下形式描述包含有非線性、內部和外部干擾、參數不確定性的被控過程：

w(t))+bu(t)

(1)

式中：t為時間；y(t)、u(t)分別為被控量和控制量；b為系統增益；g(·)為非線性綜合函數，包含了y(t)的各階導數、外部擾動w(t)和內部擾動d(t)。

定義總和擾動f(t)為：

f(t)=g(·)+(b-b0)u(t)

(2)

式中：b0為b的估計值。

則被控過程(1)可寫為：

(3)

假設f(t)是可導的，則可設計Ⅱ階擴張狀態觀測器對其進行估計，表達式為：

(4)

式中：z1(t)和z2(t)為ESO的狀態量，分別用于對y(t)和f(t)的觀測；β1和β2為觀測器參數。

設計控制律為：

(5)

式中：kp為控制器參數；r(t)為設定值。

當ESO觀測精度較高，且z1→y，z2→f時，將式(5)代入式(3)可得：

(6)

閉環系統近似的預期響應速度可通過kp調整，其預期動態特性表達式為：

(7)

式中：Gcl(s)為閉環預期傳遞函數；Y(s)和R(s)分別為y(t)和r(t)的拉普拉斯變換；s為復變量。

Ⅰ階線性ADRC的結構如圖1所示。

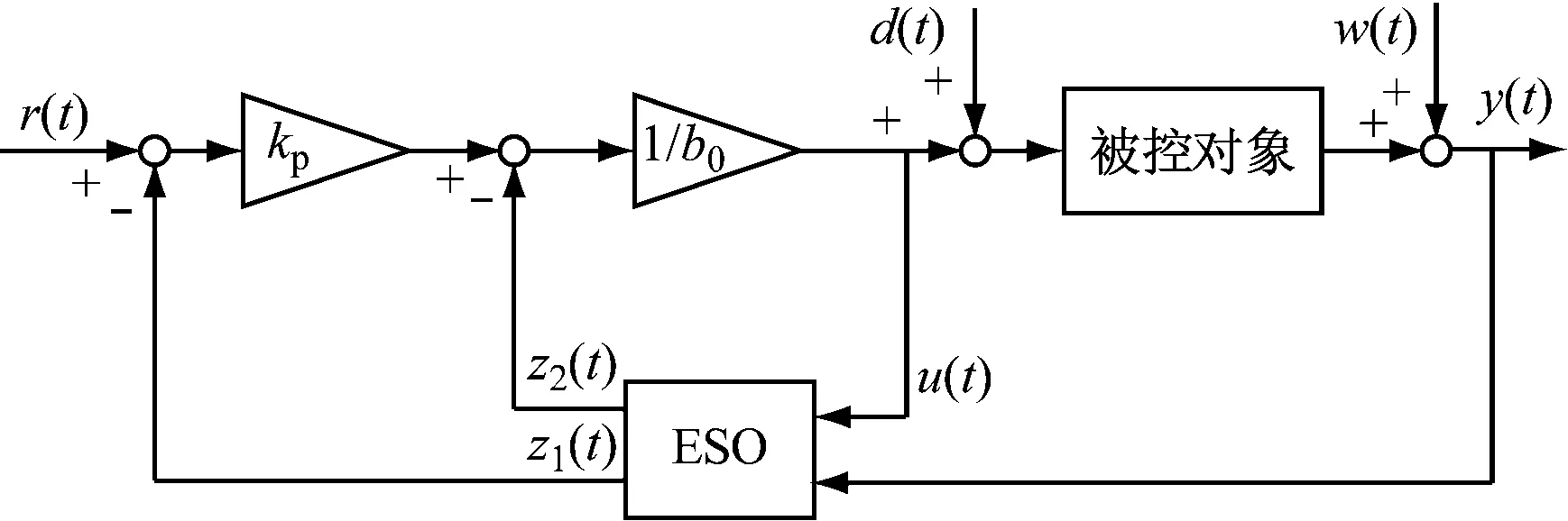
圖1 Ⅰ階線性ADRC結構

其控制器參數kp和擴張狀態觀測器參數β1、β2可采用帶寬參數化[9]的方法整定，即選擇控制器帶寬ωc和觀測器帶寬ωo，通過下式計算獲得：

(8)

Ⅰ階線性ADRC的實現形式和參數整定均較為簡單，但如果用于大慣性大時滯對象控制，因觀測效果不理想，無法獲得理想的預期動態特性，存在響應偏慢的問題，因此提出了基于模型信息的改進設計方法。

1.2 自抗擾控制器結構改進

為簡化設計和分析，設被控過程近似為n階慣性環節形式，其傳遞函數如下：

(9)

式中：G(s)為被控過程的傳遞函數；K為傳遞函數增益；T為時間常數；n為系統階次。

利用此預估模型，設計補償環節為：

(10)

式中：Gcp(s)為補償環節的傳遞函數；Tf為補償環節的時間常數；m為補償環節的階次；Uf(s)和U(s)分別為補償環節輸出uf(t)和輸入u(t)的拉普拉斯變換。

含補償環節的自抗擾控制結構如圖2所示。

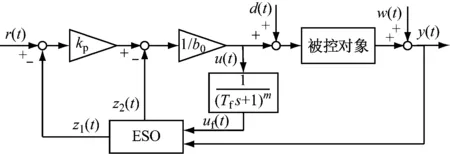
圖2 ADRC的改進結構

若取Tf=T，m=n，經補償后ESO觀測的等價系統為：

(11)

即經過補償后的等價對象是放大系數為K的環節。

此時，ESO可改寫為：

(12)

控制律仍采用式(5)的形式。通過選擇合理的控制器參數，既可獲得近似開環階躍響應的閉環動態響應，又能兼具抗擾能力和一定的魯棒性。

1.3 參數整定

在圖2所示的補償結構下，ADRC可調參數為b0、ωc和ωo。以下通過分析給出各參數的選取方法。

1.3.1b0取值

根據式(3)可知，b0表征的是控制作用對系統Ⅰ階導數增益的估計值，由式(11)可得：

(13)

由式(3)可知，本文ADRC的總和擾動表達式應為：

(14)

對比式(13)與式(14),令：

(15)

為簡化整定，可近似取b0=K，誤差部分作為總和擾動的一部分，利用ESO進行觀測和補償，即

(16)

1.3.2ωc取值

由式(11)可知，補償后ESO觀測的等效對象傳遞函數為K，因此控制作用應取比例作用1/K；Ⅰ階線性ADRC的比例作用可視為ωc/b0，因此ωc的取值應為b0/K；由于b0=K，因此ωc值取為1。

1.3.3ωo取值

ωo的大小反映了觀測器對系統狀態的跟蹤速度；如果ωo過小，觀測器對于狀態的觀測跟蹤過慢，使得系統閉環動態響應較慢，且魯棒性較差；如果ωo過大，會突出高頻噪聲的影響，造成控制量的不必要動作。因此ωo一般取為10ωc。

綜上所述，基于模型補償的ADRC控制參數可按如下步驟確定:

(1) 獲得被控過程的預估模型G(s)=K/(1+Ts)n。

(2) 設計補償環節Gcp(s)=1/(1+Tfs)m，并取Tf=T，m=n。

本文的ADRC參數整定方法非常簡潔，且參數物理意義清晰明確，同時保留了Ⅰ階線性自抗擾控制器結構簡單、易于在工業控制系統上實現的優勢，因此具有非常好的工程應用潛力。此外，這種設計方法同樣適用于有自平衡能力的非最小相位對象，只需在設計補償環節時使得ESO觀測到的系統為“1”即可。

2 仿真分析

為驗證上述控制方法的性能，以文獻[10]中某超超臨界機組過熱汽溫惰性區被控過程為例進行仿真分析，傳遞函數為G(s)=1.202/(27.1s+1)7。

將本文設計的ADRC、按文獻[11]整定的ADRC(以下記為LADRC)、基于Skogestad Internal Model Control (SIMC)[12]法整定的PI控制器(以下記為SIMC-PI)及開環控制進行對比，各控制器參數整定結果見表1。

表1 各控制器參數

本文中的開環控制相當于開環響應，僅用于反映被控過程開環階躍響應的變化快慢，作為動態過程的參照。SIMC-PI是基于Ⅰ階慣性加純滯后(FOPTD)模型進行設計的方法，需先將高階被控過程近似為FOPTD形式，因此先將傳遞函數近似為Ga(s)=1.21e-87.83s/(103.68s+1)，再根據結果整定SIMC-PI的控制參數。

2.1 控制效果對比

采用固定步長為0.1 s進行仿真。設定值階躍和擾動階躍下，上述方法的控制效果對比如圖3所示。根據仿真結果，通過計算得到的各控制器性能指標見表2，其中σsp和Ts,sp分別為設定值階躍下的超調量和調節時間，σud和Ts,ud分別為擾動階躍下的最大動態偏差和調節時間，JIAEsp和JIAEud分別代表設定值階躍和擾動階躍下的絕對誤差積分指標(2%誤差標準)。

(a) 被控量曲線

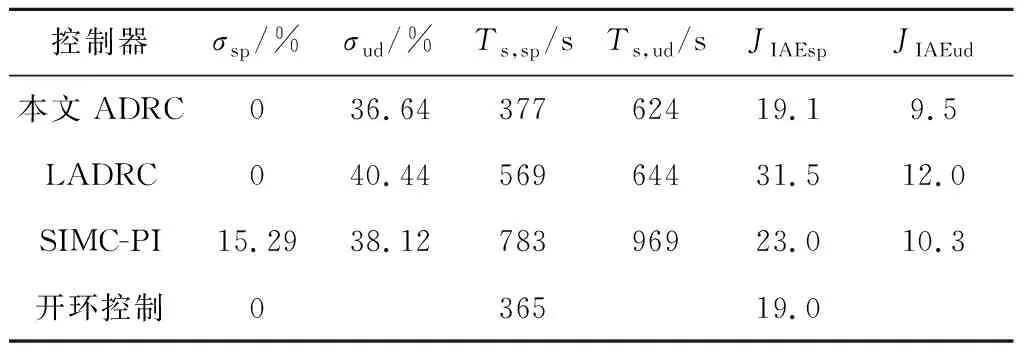
表2 各控制器性能指標

從圖3和表2可以得出：(1) 相比于LADRC和SIMC-PI控制器，本文設計的ADRC綜合控制性能更好，絕對誤差積分指標JIAEsp和JIAEud均為最優，調節時間最快，擾動影響幅值最小且跟蹤過程未超調，由此可得，改進設計方法可以改善ADRC的控制效果；(2) 本文設計的ADRC設定值跟蹤過程基本與作為參照的開環控制一致，驗證了前文理論分析的正確性。

仿真結果表明，當執行機構速率受到限制時，本文設計的ADRC閉環階躍響應基本與考慮執行機構速率后的開環階躍響應一致，能達到設計的預期動態。

2.2 魯棒性能對比

由于被控過程的參數具有不確定性，需要檢驗所設計控制器的性能魯棒性。保持控制器參數不變，設被控過程的系統參數T和K在標稱值±25%范圍內隨機變化，服從均勻分布，對各控制器開展Monte Carlo實驗。仿真實驗重復1 000次，統計各控制器的綜合指標JIAEsp和JIAEud，結果如圖4所示。性能指標越小表示設定值跟蹤和抗干擾性能越好，分布越密集表示性能魯棒性越強。

由圖4可知，在參數不確定性下，ADRC方法和LADRC方法的性能指標變化范圍均小于SIMC-PI；其中本文設計的ADRC魯棒性最好，其設定值跟蹤和抗干擾的性能魯棒性均優于LADRC和SIMC-PI控制器，說明雖然本文設計方法利用了模型信息，但仍具有優良的性能魯棒性，保證了系統對不確定性的適應能力。

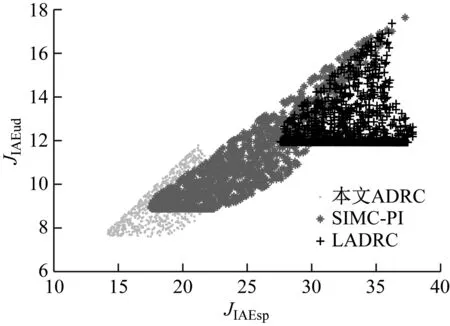
圖4 參數不確定性下各控制器的性能指標分布

3 現場應用

根據上述分析和仿真研究，將本文ADRC方法應用于國能蚌埠發電有限公司660 MW二次再熱3號機組的1號高壓加熱器水位和過熱汽溫Ⅰ級減溫噴水控制回路，基于現場集散控制系統(DCS)進行了自抗擾控制器的組態實現、參數整定和控制效果測試。

3.1 高壓加熱器水位控制

該機組1號高壓加熱器水位控制回路原有PID調節器參數為kp=0.3,ki=1/130。利用閉環辨識方法獲得水位被控過程近似傳遞函數為G(s)=14.5/(85.3s+1)，由此獲得本文所提出的自抗擾控制器參數為ωc=1，b0=14.5，ωo=10，Tf=85.1，m=1。

在DCS系統中設置了自抗擾控制器與PID控制器無擾切換邏輯，分別進行了抗擾實驗和設定值跟蹤實驗。

3.1.1 抗擾實驗

負荷在620～660 MW范圍內波動時，分別將控制方式設置為ADRC控制和PID控制，水位偏差絕對值的最大值JAEmax、平均值JAEave和標準差JAEdev見表3。由表3可知，1號高壓加熱器水位投入ADRC控制后，最大絕對偏差較原PID控制下降了34.0%，平均絕對偏差下降了40.0%，偏差的標準差下降了40.2%。

表3 高壓加熱器水位控制偏差對比

負荷擾動下的高壓加熱器水位變化曲線如圖5所示。由圖5可知，ADRC控制在負荷波動下的動態偏差更小，顯示出良好的抗擾性能。

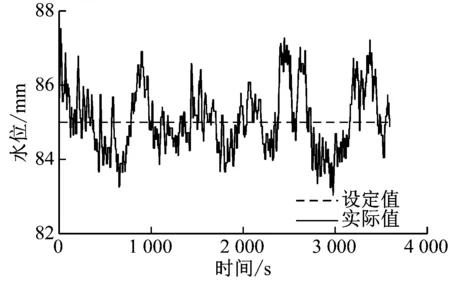
(a) PID控制曲線

3.1.2 設定值跟蹤實驗

分別在ADRC控制和PID控制方式下，令高壓加熱器水位設定值發生±5 mm的階躍變化，實際水位變化曲線如圖6所示，超調量和調節時間見表4。與原PID控制器相比，1號高壓加熱器水位投入ADRC控制后的設定值跟蹤下降了78.2%，調節時間縮短了54.4%，顯示出良好的設定值跟蹤性能。綜上可知，本文設計的ADRC控制器對高壓加熱器水位的控制品質有顯著改善。

(a) PID控制曲線

表4 高壓加熱器水位設定值跟蹤性能對比

3.2 Ⅰ級過熱汽溫控制

將本文設計的ADRC應用于該機組B側過熱汽溫Ⅰ級噴水減溫(即屏式過熱器出口汽溫)控制，該控制系統采用串級控制結構。考慮到串級控制的外環對應惰性區慢對象，而內環對應導前區快對象，內環的閉環傳遞函數可近似為1，將外環PID控制器改為ADRC控制器。

根據歷史運行數據曲線，估算出外環被控過程可近似為G(s)=0.5/(30s+1)4，通過計算獲得ADRC控制器參數為：ωc=1，ωo=10，b0=0.5，Tf=30，m=4。投入ADRC控制系統并運行一段時間后，與歷史數據庫中工況相似的PID控制進行對比，如圖7和圖8所示。圖7(a)～圖7(d)為采用ADRC控制后2021年4月8日的運行曲線，對應負荷變化范圍約為600～660 MW；圖8(a)～圖8(d)為采用PID控制后2021年3月23日的運行曲線，對應的負荷變化范圍也為600～660 MW。

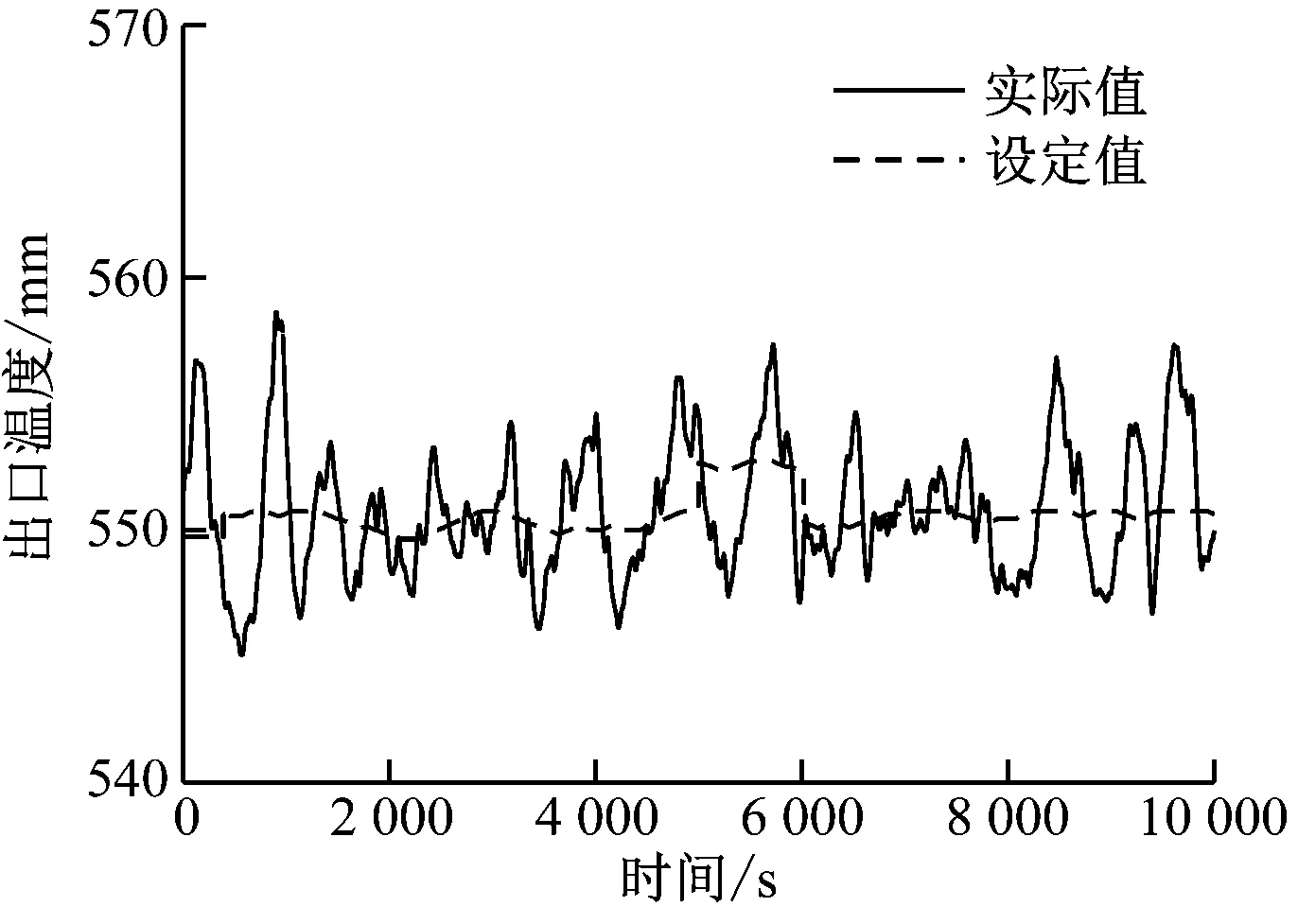
(a) 屏式過熱器出口溫度

汽溫控制偏差絕對值的最大值JAEmax、平均值JAEave和標準差JAEdev見表5。由表5可知，與原PID控制相比，機組B側Ⅰ級過熱汽溫投入ADRC控制后的最大偏差下降了56.9%，平均偏差下降了75.6%，偏差的標準差下降了72.5%，該回路的控制品質得到了提高；運行人員手動偏置次數由12次減少為2次，大幅減小了運行人員的壓力。

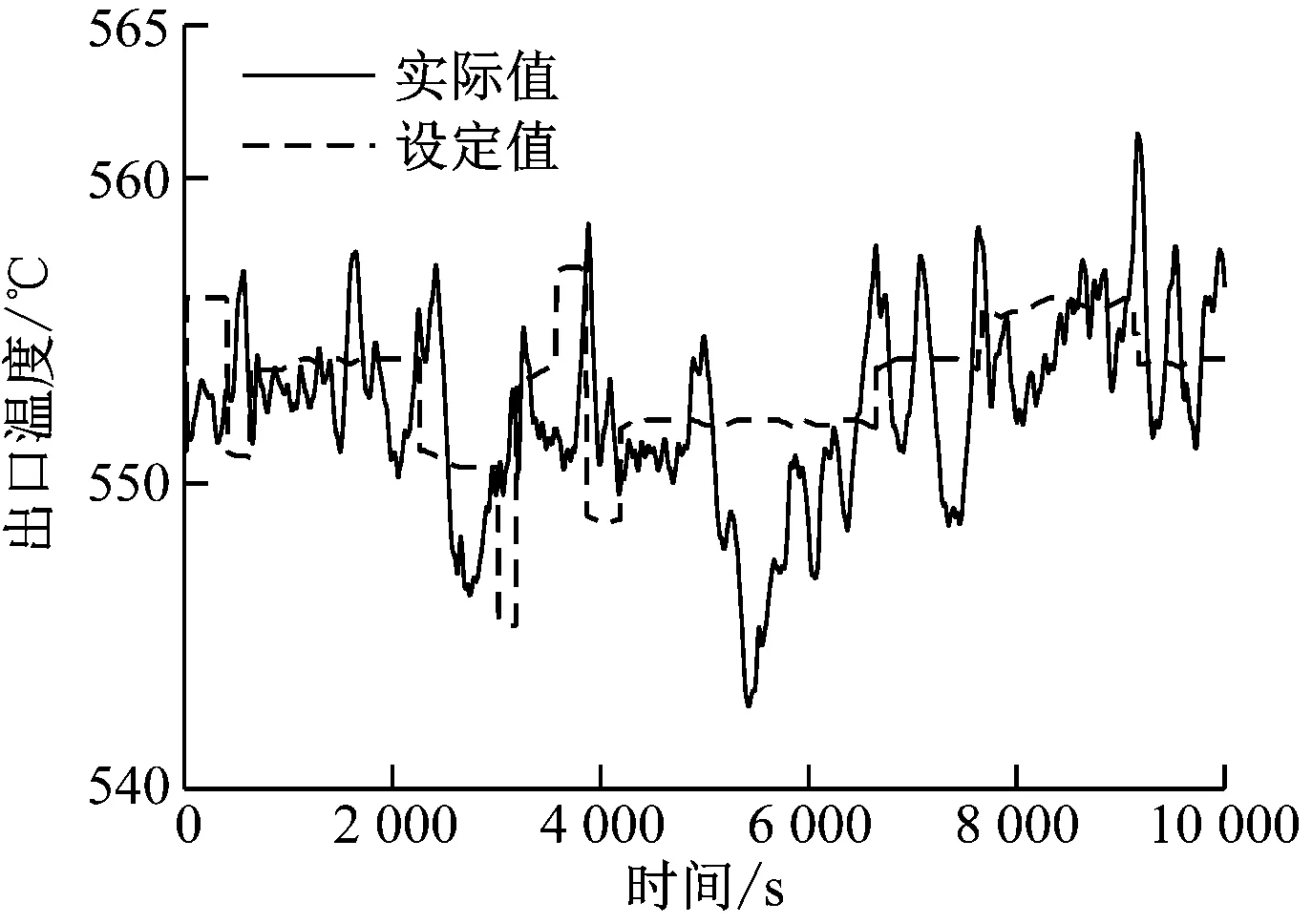
(a) 屏式過熱器出口溫度

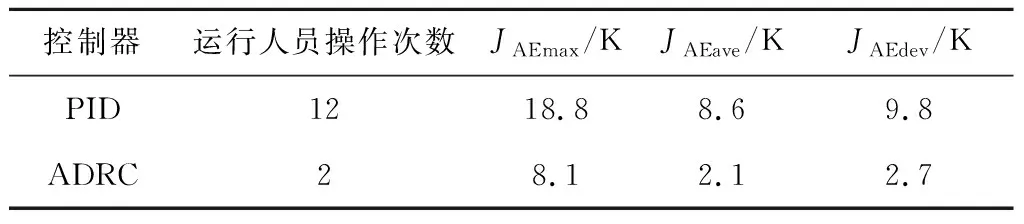
表5 Ⅰ級過熱汽溫控制偏差對比

4 結 論

針對線性自抗擾控制器應用于熱力過程存在大慣性、對象響應偏慢的問題，提出了基于預估模型信息的改進設計方法，并給出了簡潔的參數整定公式。仿真結果表明，所設計的自抗擾控制器可以加快閉環系統的動態響應，同時兼具良好的抗擾能力和系統魯棒性。將本文方法應用于某火電機組高壓加熱器水位控制和過熱汽溫控制，現場實驗結果表明，相較于原有PID控制器，所設計的控制器改善了系統的控制性能，且其實現和整定簡便，具有很好的工程應用潛力。