基于深度前饋神經網絡的多因子人體表面積計算模型*

王雨露，李 飛，楊 震，黃 山，張 罡，詹 曙

(1.大數據知識工程教育部重點實驗室(合肥工業大學),安徽 合肥 230601；2.合肥工業大學計算機與信息學院,安徽 合肥 230601；3.安徽醫科大學第二附屬醫院,安徽 合肥 230601)

1 引言

人體表面積BSA(Body Surface Area)是一個十分重要的生理參數，在許多醫學應用中有著至關重要的作用。一方面，它作為標準化的衡量標準，在腫瘤治療中細胞毒性和細胞抑制藥物的劑量等方面起著決定性作用[1,2]。有研究證明了基于BSA的治療藥物劑量計算的有效性，并強調了其最重要的好處是患者存活率的提高[3]。在燒傷的情況下也需要使用BSA來評估皮膚損傷的嚴重程度，用來預測患者的生存幾率[4]。另一方面，BSA在臨床上廣泛用于計算腎小球濾過率[5,6]，是腎病綜合癥治療中的主要變量。BSA在腎移植術后受者早期腎功能康復領域受到了廣泛的關注[7,8]。但是，由于人體形態的復雜性和不規則性，通過實際測量來獲取BSA是不現實的。因此，如何有效地計算BSA是十分有意義的。在過去的兩百年里，人們從未停止過對人體表面積的探索。1848 年，Bergmann和Rubner首次提出動物體熱的產生與體表面積成正比，在此之后人體表面積的研究開始一步步向前發展。Meeh[9]提出了第1個可以使用的BSA計算方法，但其只考慮了體重這一變量。Du Bois等[10]提出的BSA計算方法引入了一個新變量—高度。隨后，許多研究人員為了獲取更準確的BSA值而不斷改進Du Bois方法的系數。為得到中國人BSA計算方法，Stevenson[11]對Du Bois公式進行了修正。隨著時間推移，胡詠梅等[12]指出Stevenson方法已經不再適用于當代中國人體表面積的計算，提出了一種新的中國人BSA計算方法。隨著3D激光表面掃描和CT掃描等技術的發展，三維測量技術已應用到BSA測量的研究中。有研究表明,三維測量BSA時的掃描誤差在1%范圍內，與傳統人工測量方法相比，三維人體測量更精確、更穩定[13]，因此可借助三維掃描得到的體表面積來推導BSA計算方法。目前已經有多種通過三維掃描技術推導出的BSA計算方法。Tikuisis等[14]借助三維全身掃描和三維建模軟件提出了分別適用于男性和女性的BSA計算方法。Schlich等[15]提出了新的分別適用于男性和女性的BSA計算方法。Yu等[16]通過3D掃描技術研究出男女性通用的BSA計算方法。隨著3D掃描技術的發展,Yu等[17]提出了新的分別適應于男性和女性的BSA計算方法。Kuehnapfel等[18]也提出了新的男女通用的BSA計算方法。表1展示了近一百年來的部分BSA計算方法(W：體重，H：身高)。

目前基于三維測量技術的人體表面積計算方法已有多種[13,19]，但仍存在以下3個問題：(1)只考慮了人體少量的參數(身高和體重，在一些特別的情況中還考慮了性別和年齡)；(2)通過匹配特定的簡單函數估計模型參數；(3)臨床上也認為現有的BSA計算方法誤差較大，對臨床治療影響較大。隨著神經網絡的發展，多種神經網絡應用于回歸預測中。醫生也希望借助深度學習的方法來計算人體表面積。基于此，本文提出了基于深度前饋神經網絡DFNN(Deep Feedforward Neural Network)的多因子人體表面積計算模型，模型由2部分組成：首先是特征選擇，通過相關性和顯著性分析的方法選擇與人體表面積相關性最高的人體影響因子；其次是深度前饋神經網絡回歸。本文研究基于安徽醫科大學第二附屬醫院提供的104組數據，與傳統BSA計算方法和3種其它方法進行實驗對比。實驗結果表明，本文方法可以得到更好的效果，證明該模型是有效的。

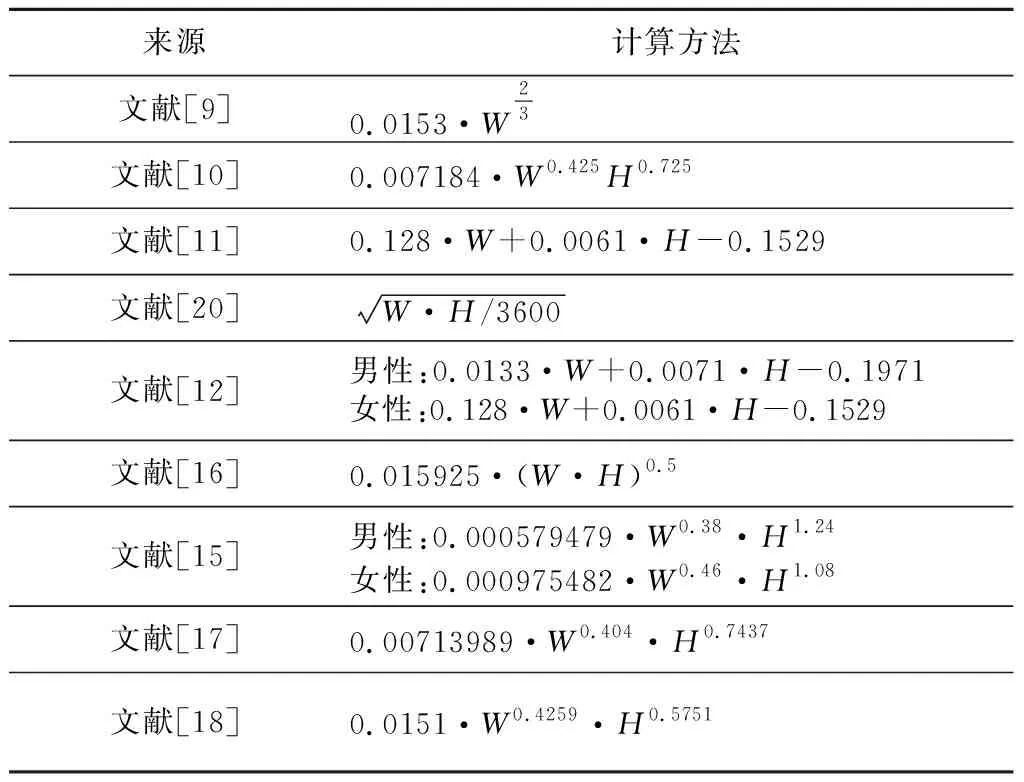
Table 1 Body surface area formulas

2 數據與方法

2.1 數據來源

本文研究使用的體表數據由安徽醫科大學第二附屬醫院提供，自2020年10月至2021年1月收集，共104組，男女比例為61∶43。在室溫下進行身高、體重和胸圍等人體數據測量。測量身高和體重等數據時，要求受試者站直并伸展身體。進行CT掃描時要求受試者將手臂盡量與身體分開一定距離，雙腿分開。CT掃描獲得人體切片數據后生成3D模型，得到3D人體模型的體表面積。

2.2 方法

2.2.1 特征變量選取

對于輸入變量來說，數量過多會導致回歸方法過于復雜，且如果引入的是無關變量，回歸方法的泛化能力會降低。因此，需要選擇合適的特征變量用于建立多元回歸方法。本文通過皮爾遜相關系數和顯著性檢驗來進行特征變量的選擇。相關系數絕對值越大，相關度越高。因為相關系數是一個隨機變量，取值具有一定的偶然性，2個不相關的變量，相關系數也可能較高，因此需要顯著性檢驗來輔助，只有當顯著性水平顯著時，相關系數才是可信的。

2.2.2 數據預處理

由于各個特征變量及人體表面積的數值差異較大，在建立回歸方法之前要先對數據進行預處理，即利用式(1)對數據進行歸一化。

(1)

其中,xmin為數據最小值，xmax為數據最大值，xi為第i個數據，xR為xi歸一化后的結果。

2.2.3 深度前饋神經網絡

深度前饋神經網絡DFNN是一種典型的深度學習方法[21]，又稱為多層感知機。DFNN的目標是將數據通過多個轉換層[22]，以分層的方式學習數據的復雜抽象表示。DFNN一般由輸入層、隱含層和輸出層這3部分組成，每一層都有若干相互關聯的處理單元。DFNN的結構如圖1所示。

Figure 1 Structure of deep feedforward neural network圖1 深度前饋神經網絡結構

在DFNN中，每一層對其輸入進行非線性轉換，并在這一層的輸出中表示。第m層第n個神經元的計算公式如式(2)所示:

(2)

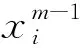
2.2.4 建立深度前饋神經網絡

深度前饋神經網絡中參數的設置如表2所示。

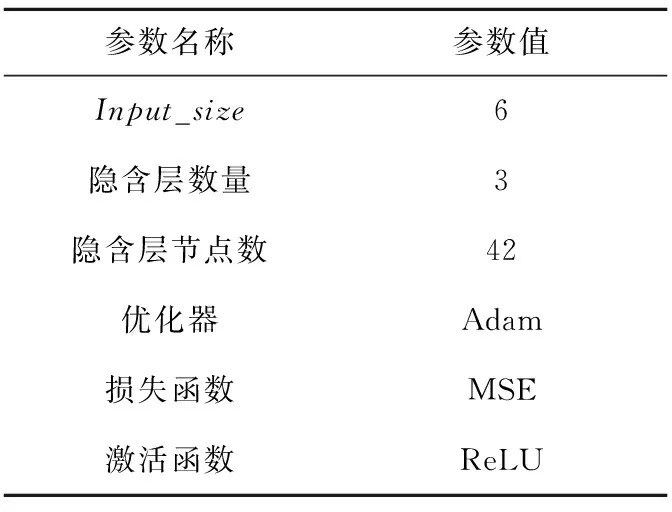
Table 2 Parameters setting of DFNN

輸入變量為根據相關性分析選擇出的6個特征變量。本文DFNN包含3個隱含層，每個隱含層包含42個節點。DFNN采用Adam(Adaptive moments estimation)算法作為優化器，均方誤差MSE(Mean Square Error)作為損失函數來進行DFNN的優化更新。對于激活函數的選擇，在神經網絡反向傳播誤差的過程中，反向傳播是逐層對激活函數的偏導進行相乘，但隨著神經網絡的層數不斷增加，容易出現梯度消失問題。為了改善DFNN的性能，本文使用修正線性單元ReLU(Rectified Linear Unit)激活函數來解決梯度消失的問題。因為ReLU函數的偏導是1，它的許多特性使網絡容易用基于梯度的方法進行優化。對于深層網絡，ReLU可以更快地進行學習，且允許訓練深度監督網絡而不需要無監督的預訓練[23]。ReLU的數學公式如式(3)所示：

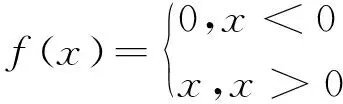
(3)

2.2.5 評價方法

為了避免網絡模型在訓練中出現過擬合和欠擬合等問題，也為了驗證方法對隨機劃分數據的可行性，本文采用5-折交叉驗證和測試集驗證2種方法進行實驗[24]。5-折交叉驗證將數據集等分為5個子數據集，每個驗證過程將其中一組子數據集作為驗證集，其余4組作為訓練集構建模型，每個子數據集都要作為驗證集驗證1次，最后5次驗證的平均得分作為方法的最終得分。5-折交叉驗證原理圖如圖2所示。測試集驗證將數據集按7∶3的比例劃分為訓練集與測試集，在測試集上測試獲得模型評價得分。

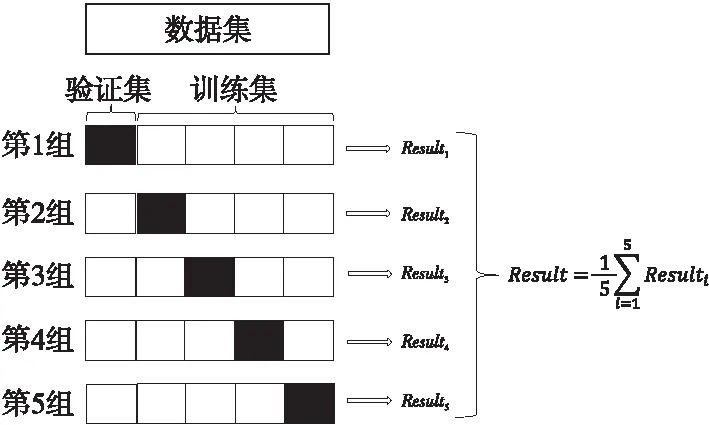
Figure 2 Five-fold cross validation圖2 5-折交叉驗證

本文使用決定系數R2評價方法的學習能力，其值越接近1，方法的學習能力越強,模擬效果越好。采用均方誤差MSE、平均絕對誤差MAE(Mean Absolute Error)以及平均絕對誤差百分比MAPE(Mean Absolute Percentage Error)3個評價指標來對預測方法進行評價。預測誤差越小，表明方法精度越高。R2、MSE、MAE和MAPE的定義分別如式(4)～式(7)所示：

(4)

(5)

(6)

(7)

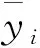
2.2.6 Bland-Altman分析法

在方法的一致性評價方面，研究表明僅用決定系數評價方法一致性是片面的[25]。因此本文研究采用Bland-Altman分析[26]評價方法的一致性。Bland-Altman分析是一種評價2種測量結果一致性的新方法，通過繪制散點圖預測結果的一致性界限，根據散點圖的一致性界限大小及落在一致性界限外的散點數來評價方法一致性。

3 實驗結果

3.1 影響因子相關性

本文借助SPSS軟件對體表數據與人體表面積進行相關性與顯著性分析，分析結果如表3所示(其中顯著性0.000指小于0.01，相關性顯著)。

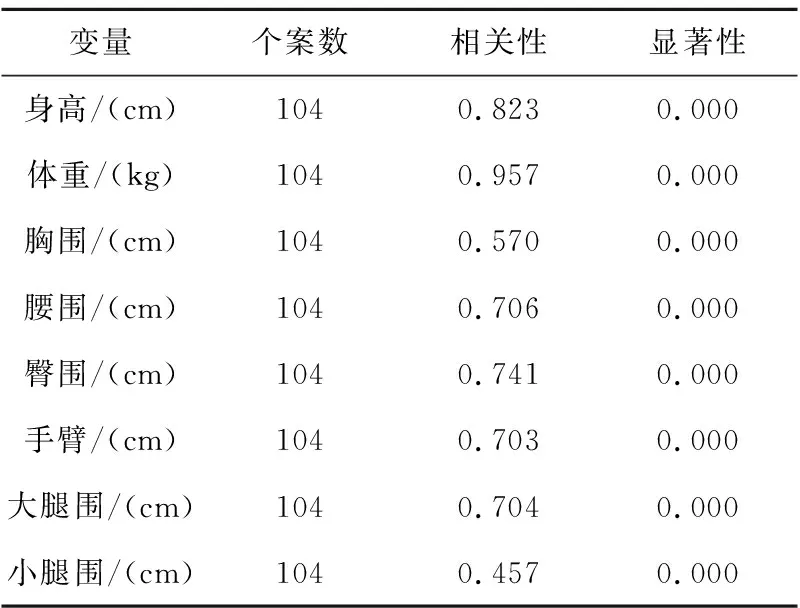
Table 3 Correlation and significance analysis of characteristic variables

根據表3內容選取相關性最高的身高、體重、腰圍、臀圍、手臂圍和大腿圍 6個變量作為輸入變量。

對學生而言，利用EDA技術進行設計和仿真，不僅能提高學生的學習興趣，鞏固課堂所學知識，而且還能提高學生的動手能力，提高學生電子實驗技能的應用水平。在電子行業中，傳統的設計過程是：首先提出設計方案，然后設計電路，制作線路板，焊接元件，最后調試，有問題時再重新設計制作，這樣不但費時費力，而且會造成大量資金的浪費。利用EDA技術可以避免這些問題的出現，提高工作效率。利用EDA技術進行實驗教學具有縮短設計周期，節省設計、實驗費用，提高設計質量等優點，因而得到了越來越多的應用［4］。

3.2 前饋神經網絡深度分析

為驗證3層前饋神經網絡的合理性，本節分別選取包含2層、4層、5層和6層隱含層的前饋神經網絡與3層前饋神經網絡進行性能對比。首先進行5-折交叉驗證，結果對比如表4所示。再將104名受試者按7∶3的比例劃分訓練集與測試集，各個方法的預測結果如表5所示。

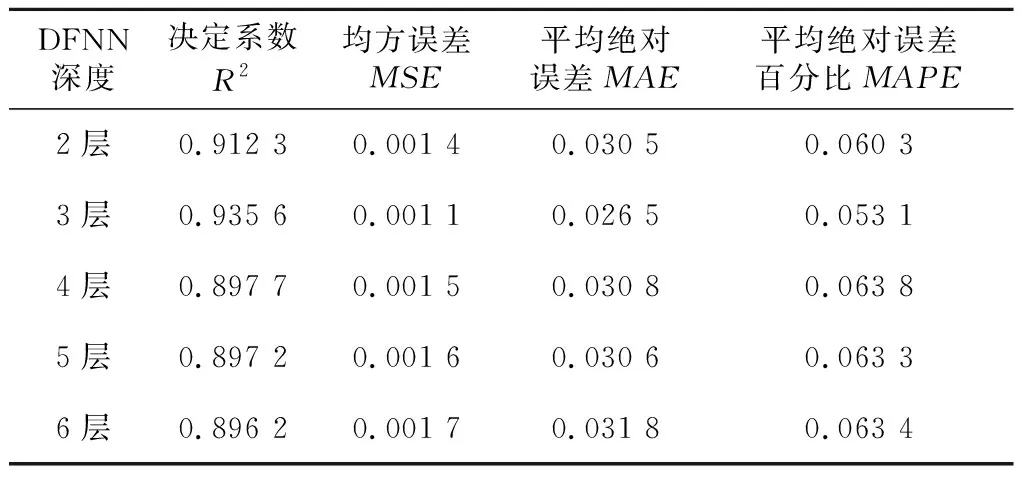
Table 4 Performance comparison of DFNN under five-fold cross validation

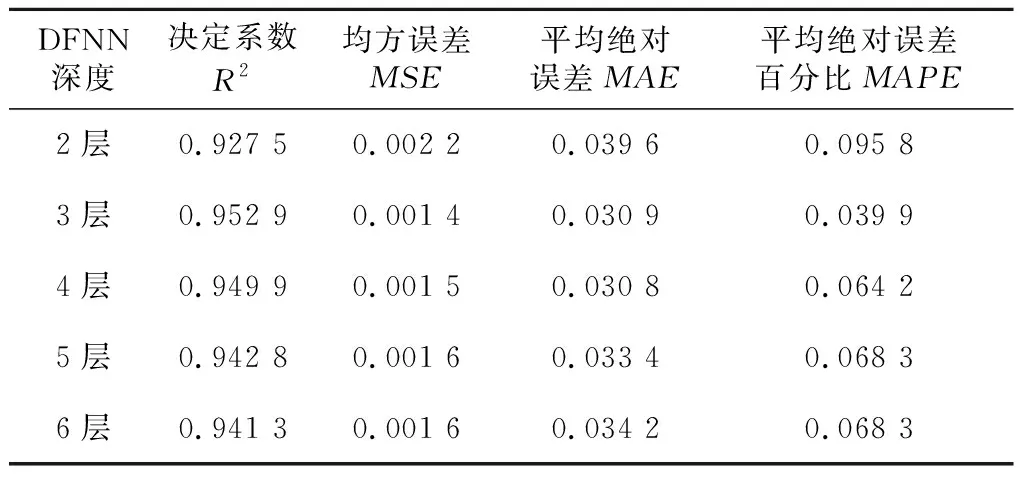
Table 5 Performance comparison of DFNN on test set

從表4和表5可以看出，與其他層數的前饋神經網絡相比，3層前饋神經網絡的R2均為最大，MSE、MAE和MAPE的值均為最小。當網絡深度由2層變為3層時，決定系數R2增大，MSE、MAE和MAPE的值均減小。而當網絡深度由3層開始逐漸增加時，決定系數R2在逐漸減小而MSE、MAE和MAPE的值呈逐漸增大的趨勢。因此，當網絡深度為3層時預測效果最好。

3.3 預測結果

3.3.1 與傳統方法比較

為驗證DFNN的效果，首先比較DFNN與傳統BSA計算方法的預測結果：對DFNN使用5-折交叉驗證，選取最新的Yu和Kuehnapfel傳統方法進行5-折交叉驗證來對比，結果如表6所示。再將104名受試者按7∶3的比例劃分訓練集與測試集，在測試集上的預測結果如表7所示。

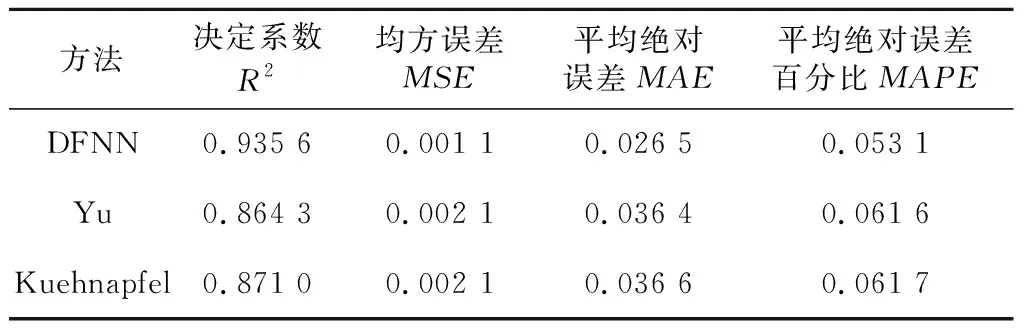
Table 6 Performance comparison with traditional methods under five-fold cross validation

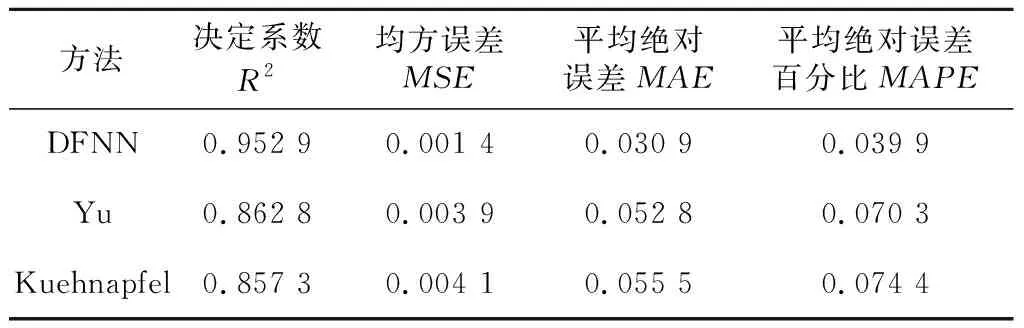
Table 7 Performance comparison with traditional methods on test set

從表6和表7可以看出，無論是在交叉驗證實驗中，還是在測試集實驗中，與傳統的Yu等計算方法和Kuehnapfel等計算方法相比，DFNN模型獲得的預測精度最高，不但決定系數R2增大，同時3個誤差評價指標也都得到了一定程度的減小。DFNN模型獲得了最大的R2值以及最小的MSE、MAE與MAPE值，這意味著DFNN的效果最好。

圖3為測試集真實值與各個方法預測值的折線對比圖。可以看出，Kuehnapfel等方法的預測值在一些點處與真實值變化規律相反；Yu等方法的預測值與真實值的差值與其他2種方法相比較大；DFNN模型預測值更貼合真實值，變化規律更相近，預測結果更準確。

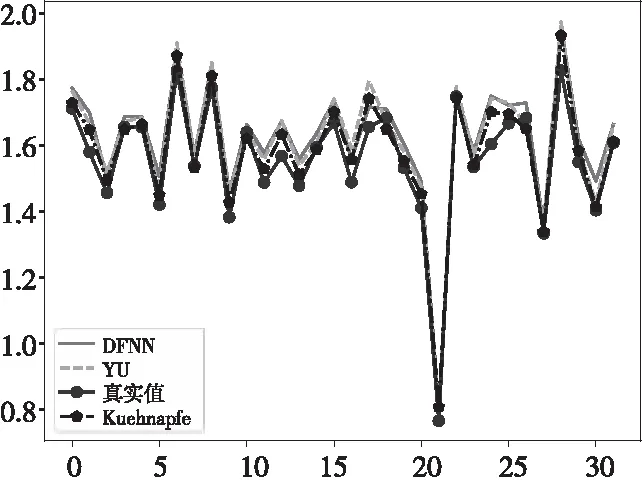
Figure 3 Comparison of real value and predicted values by traditional methods on test set圖3 測試集真實值與傳統方法預測值對比

3.3.2 與其它方法比較

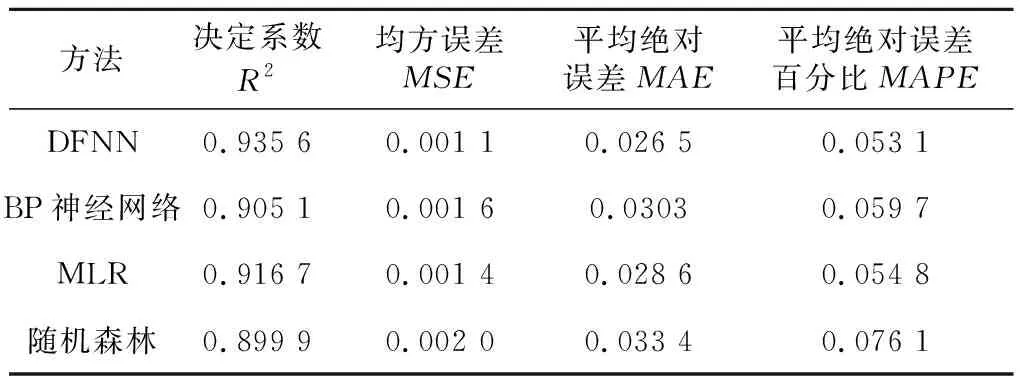
under five-fold cross validation

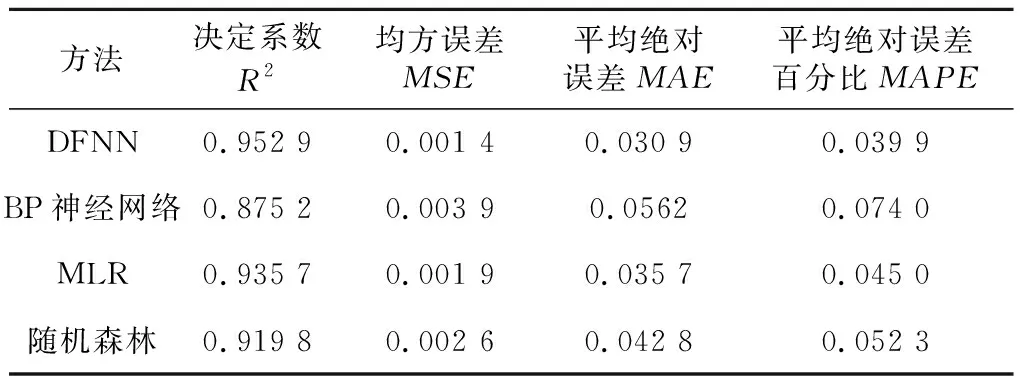
Table 9 Performance comparison with other methods on test set

從表8和表9可以看出，在構建的4種網絡預測方法中，神經網絡模型與多元線性回歸模型的預測效果均好于隨機森林回歸模型的；DFNN的決定系數R2最大，MSE、MAE和MAPE的值均為最小，交叉驗證與測試集驗證方法下均是如此。DFNN的決定系數R2更接近1，模擬效果更好，預測值更接近實測值，DFNN的各項誤差更小，表示方法精度更高，預測值更加可信。因此，與BP神經網絡、MLR模型和隨機森林相比，DFNN預測的效果最好、精度最高。

圖4為測試集真實值與各個方法預測值的折線對比圖。可以看出，雖然各個方法預測效果與真實值走向均大體相同，但隨機森林的預測值與真實值偏差最大且在某些點處走向不同，BP神經網絡和MLR預測值與真實值偏差較大，而DFNN預測值折線最貼合真實值折線，變化規律更相近，預測結果最準確。

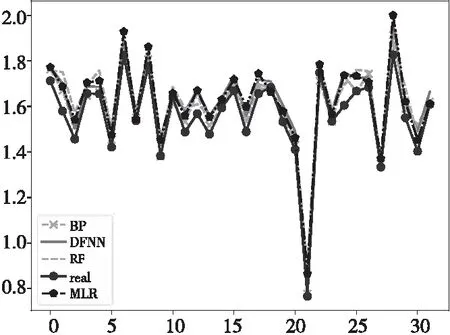
Figure 4 Comparison of real value and predicted values by other methods on test set圖4 測試集真實值與其它方法預測值對比

3.3.3 一致性分析

為了更準確地分析各BSA預測方法的一致性，本文采用Bland-Altman分析法，以每種方法的人體表面積預測值與人體表面積真實值的均值為橫坐標,兩者之間的差值為縱坐標,繪制Bland-Altman分析散點圖。DFNN預測方法與其它對比BSA預測方法的散點圖如圖5所示，圖中方法名稱均代表使用此方法得出的體表面積。由散點圖可以看出，在所有的對比方法中，DFNN預測方法的95%一致性界限范圍最小，這意味著DFNN方法的一致性最好。

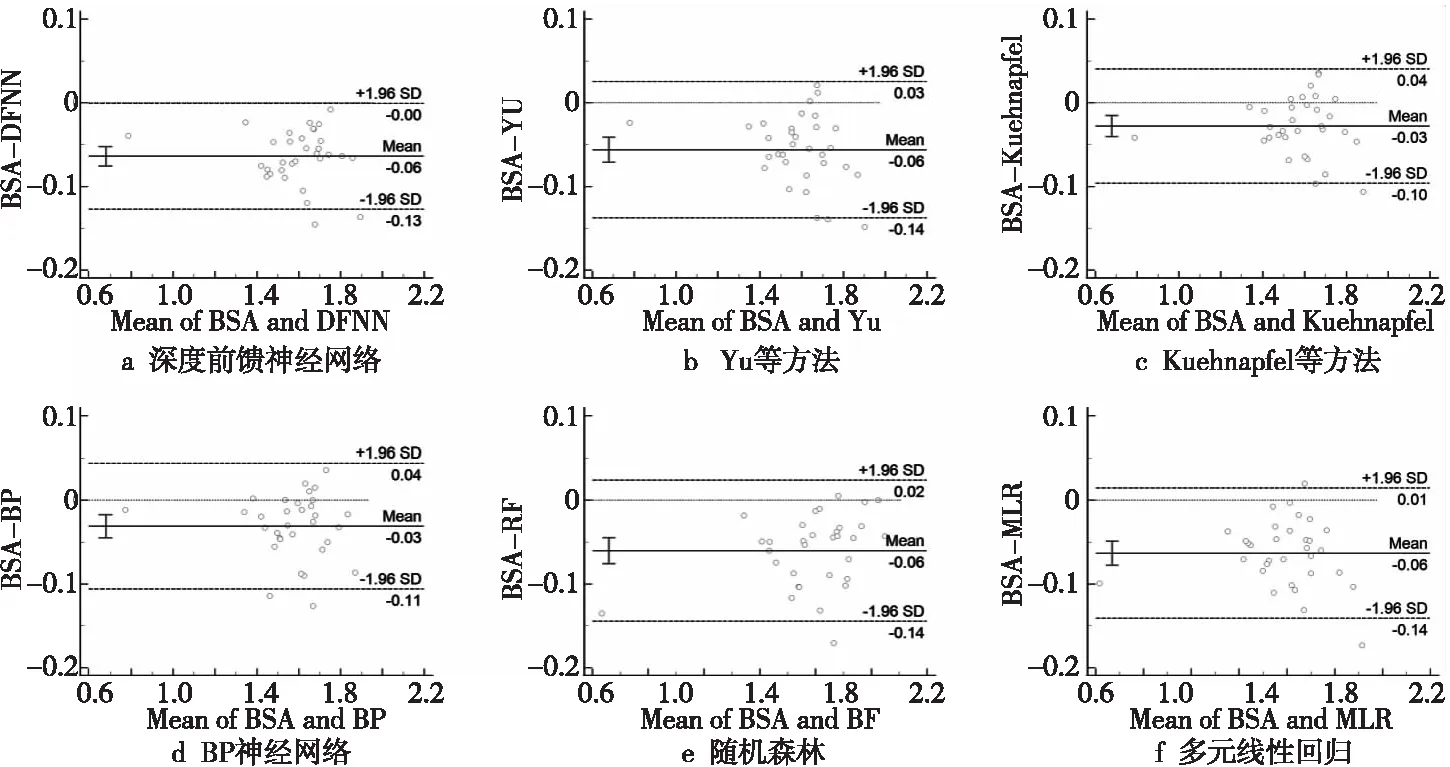
Figure 5 Bland Altman scatter plots 圖5 Bland-Altman散點圖

4 討論

BSA在醫學等領域有著極其重要的應用價值，在用藥劑量選擇、計算腎小球濾過率以及燒傷評估等方面起著十分重要的作用。然而現有BSA計算方法只考慮了人體少量參數，另外通過匹配特定的簡單函數來估計方法參數，誤差較大。三維測量獲得的BSA更精確穩定，但三維測量大多昂貴且耗費時間較多，且這些測量(例如CT掃描)對人體輻射較大。本文提出了一種有效的方法來實現BSA臨床計算，幫助醫生更快更精確地獲得病人體表面積，并通過多個實驗證明了其有效性。首先，通過相關性分析選出6個與BSA相關性最高的影響因子，與之前的BSA計算方法相比，增加了幾種不同的特征，這是降低體表面積計算誤差的重要措施；然后，建立DFNN預測方法，實現BSA自動預測。

在與傳統方法的比較中，本文選擇了最新的Yu和Kuehnapfel計算方法進行對比。從實驗結果可以看出，3種方法中DFNN的精度最高，誤差最小，預測效果最好。這主要是因為借助相關性分析選取了與BSA相關性最高的特征變量，增加了人體參數，提高了預測精度。此外，神經網絡不僅可以學習特征變量與BSA之間的關聯，還可以自動從簡單特征中學習提取到更深層、復雜的特征，既避免了傳統的復雜計算也提高了BSA預測方法的精度，從而獲得了更加精確的預測值。

在與其它方法的比較中，本文對DFNN、BP神經網絡、MLR和隨機森林進行BSA回歸模型構建。結果表明，DFNN回歸方法預測結果優于BP神經網絡、MLR和隨機森林模型的。DFNN使用ReLU激活函數，避免了梯度消失問題，通過使用帶標簽的數據進行訓練，誤差自上到下傳播，利用誤差來調整各層之間的權重，使得4種方法中DFNN獲得了最高預測精度。根據Bland-Altman散點圖也可以看出，DFNN在所有方法中95%一致性界限范圍最小，一致性最好。

本文使用的樣本數據量較小，還需要收集更多的體表數據以進一步優化模型。未來，隨著樣本數據增加，在大數據條件下選擇構建合適的方法進行訓練，以獲得更高的BSA計算精度，提出更全面、適合不同種族的BSA計算方法。

5 結束語

為得到BSA的精確預測值，本文研究針對以往BSA計算方法指示性狀較少的問題進行改進，借助相關性分析選擇6個相關性較高的影響因子參與BSA預測計算，同時引入DFNN來構建回歸模型計算BSA。在交叉驗證與測試集驗證的情況下，深度前饋神經網絡分別與2種傳統計算方法和3種其它方法進行比較，并進行了一致性分析。所有實驗結果表明，本文所提出的回歸方法能獲得最高精度的預測值，能最準確地計算BSA，給予臨床醫學最好的幫助。