一種矩陣分塊的GNSS相位模糊度快速解算方法

李克昭 朱國庫

1 河南理工大學測繪與國土信息工程學院，河南省焦作市世紀路2001號，454003 2 北斗導航應用技術協同創新中心，鄭州市科學大道62號，450001

在目前諸多GNSS定位模糊度求解方法中，以降相關思想為核心的LAMBDA算法應用最為廣泛[1-2]。LAMBDA算法解算模糊度的步驟主要包括：模糊度降相關、模糊度搜索和模糊度檢驗。其中，模糊度降相關過程涉及大量矩陣運算，耗時較長。為此，學者們進行了大量研究：Chang等[3]和Borno等[4]分別利用貪心算法和部分元素降相關方法對LAMBDA算法進行改進；Liu等[5]通過上下三角過程構造聯合去相關算法，降低模糊度之間的相關性；徐琦等[6]通過對比分析認為，聯合去相關法的處理成功率高于迭代法；Xu[7]使用Cholesky分解構建整數高斯矩陣，結果表明，在高維情況下分解得到的浮點解協方差矩陣條件數最小；陳樹新[8]以降低協方差矩陣的條件數為準則，提出一種性能更加優越的模糊度去相關算法；Liu等[9]通過三次差分測量得到模糊度浮動解，通過降低模糊度協方差矩陣的維數對搜索空間進行去相關處理，克服了Z變換可能帶來的矩陣病態分解，減少了20%的解算時間。還有學者研究不同的排序算法對降相關性能的影響[10-14]。 Hassibi等[15]將格理論中的規約算法Lenstra-Lenstra-Lovász(LLL)應用于模糊度降相關的研究中，此后大量學者對LLL算法進行了詳細研究與分析，并開展相應的改進和優化[16-22]。

綜上可知，減少矩陣的復雜運算是提高降相關效率的重要手段之一。LAMBDA算法的模糊度降相關過程主要包括Cholesky分解和矩陣降相關2個步驟。其中，傳統Cholesky分解過程復雜，會造成大量計算冗余；矩陣降相關過程主要為條件方差排序計算，每次排序計算都需要對非主對角元素進行降相關處理，涉及大量復雜運算。基于此，本文提出一種分塊最小二乘模糊度降相關(BLAMBDA)算法：采用條件方差分塊算法優化降相關過程，對條件方差矩陣進行分塊，減少條件方差排序次數，并在此基礎上對Cholesky分解公式進行整合，減少Cholesky分解過程中的數乘運算。

1 整數最小二乘去相關算法模型

(1)

式中，a為模糊度整數候選向量。

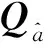
(2)

(3)

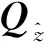
(4)

(5)

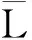
(6)

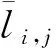
2 BLAMBDA算法求解整周模糊度

為滿足式(4)，LAMBDA算法在條件方差交換時需按照從后往前的順序排列。當遇到判別交換的條件方差dk和dk+1相差過大時，dk+1、dk+2及之前的交換過程可能不再滿足條件，需要對其進行再次交換，此過程會發生大量重復交換的情況，并增加元素降相關的運算時間。基于此，本文對條件方差矩陣進行分塊處理，使條件方差在塊內交換，通過改變交換維數和方式來減少條件方差的交換次數，并對Cholesky分解過程進行優化處理，提出改進的LAMBDA算法。

首先，對式(5)LTDL分解中的D矩陣進行分塊處理：

(7)

將n維矩陣D分成m塊(R1,R2,…,Rm)，前(m-1)塊的大小為k,Rm的大小為r=n-(m-1)k,r為不足分塊大小的部分。任意分塊Ri(1≤i≤m)和Rm可表示為：

(8)

(9)

BLAMBDA算法若不滿足式(6)，則僅在各分塊內進行交換。由于各分塊的維數較低，因此在分塊內更容易滿足式(4)，使得各分塊條件方差交換次數之和遠小于LAMBDA算法降相關過程中條件方差的交換次數，減少了大量矩陣運算和高斯變換過程。以di和di+1進行一次條件方差交換為例，減少的計算過程公式推導如下：

(10)

令

(11)

則有：

(12)

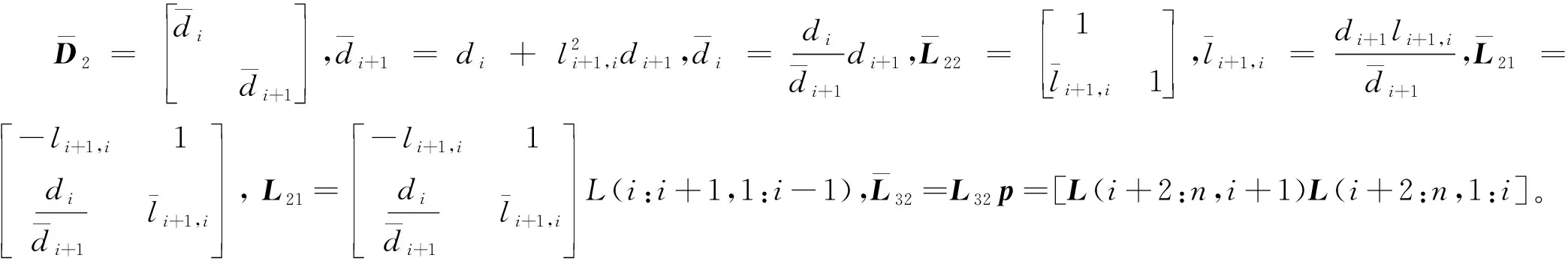
在各分塊內完成交換后，需要對相鄰塊進行條件方差交換，完成條件方差的塊傳遞。相鄰塊條件方差交換條件為：

δ(d(i-1)k+1×d(i-1)k+2×…×dik)>

dik+1×dik+2×…×d(i+1)k

(13)

式中，δ為條件約束因子，其大小決定了相鄰塊是否需要使用相鄰塊傳遞的對稱旋轉策略[3]。

當相鄰塊不滿足式(13)時，需要對Ri的第1個元素d(i-1)k+1和Ri+1的最后1個元素d(i+1)k進行交換。當Ri中的條件方差遠小于Ri+1時，需使用一次對稱旋轉策略，此過程會使2分塊內的條件方差大致按降序排列；否則僅對Ri和Ri+1的相鄰元素dik和dik+1作比較交換處理，實現相鄰塊的交換傳遞。交換公式為：

(14)

(15)

雖然在塊之間的傳遞過程中使用對稱旋轉策略會增加部分計算量，但該計算量遠小于條件方差交換過程中減少的計算量。

為進一步減少BLAMBDA算法的矩陣運算耗時，對LAMBDA算法的分解算法進行優化，即(ModifyLTDL,MLTDL)。優化策略如下：

(16)

式中，

qn=dn，qT=lTdn，l=q/dn

(17)

Q=Q-lTdnl=LTDL

(18)

將式(17)代入式(18)中，得：

Q=Q-qTl=LTDL

(19)

從式(16)～(19)可以看出，該迭代過程中沒有開平方根運算，且式(19)在式(18)的基礎上減少了數乘運算。

3 實驗驗證與分析

本文利用MATLAB 2014構建算法的仿真實驗平臺，基于Visual Studio 2019 C語言進行實驗的整體解算。計算機系統為Windows 10，處理器為8 GB內存的Intel(R) Core(TM) i7-8550U CPU@1.80 GHz 1.99 GHz。在實際解算過程中，基于RTKLIB進行基線解算，短基線的雙差模糊度整體高于中長、長基線的雙差模糊度。實測實驗以代表性實測數據(長、中長、短基線)為例進行深入分析，具有更強的說服力。

3.1 仿真實驗分析

仿真實驗的方差協方差矩陣不依賴于特定衛星和接收機的幾何構圖及定權方式，能更全面地檢驗BLAMBDA算法。構造方法如下：

(20)

式中，randn(n,1)為隨機函數生成的符合正態分布的n個隨機數。

首先對2種LTDL分解方法進行仿真實驗，仿真維數為6～40維。為避免偶然性，對每組仿真數據的2種分解方式各模擬100次，求取時間的平均值。圖1為BLAMBDA算法中改進后的MLTDL分解算法與LAMBDA算法中LTDL分解算法的解算時間對比。

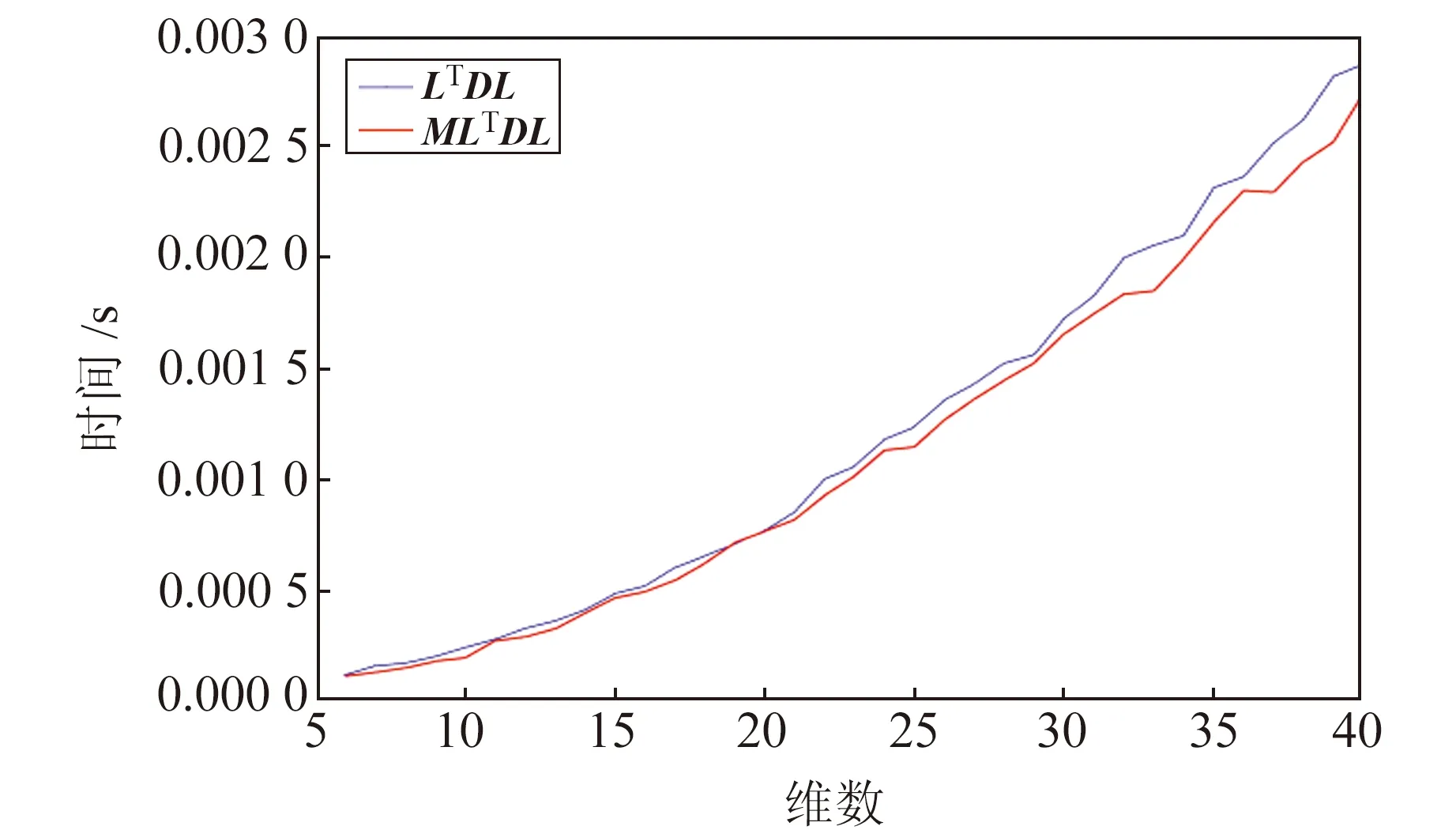
圖1 2種分解算法的平均運行時間Fig.1 Average running time of two decomposition algorithms

為更直觀地說明BLAMBDA算法能夠減少條件方差交換次數，僅對條件方差矩陣進行分塊處理，模擬方式與圖1相同，實驗結果如圖2所示。BLAMBDA算法和LAMBDA算法整體降相關耗時對比如圖3所示。

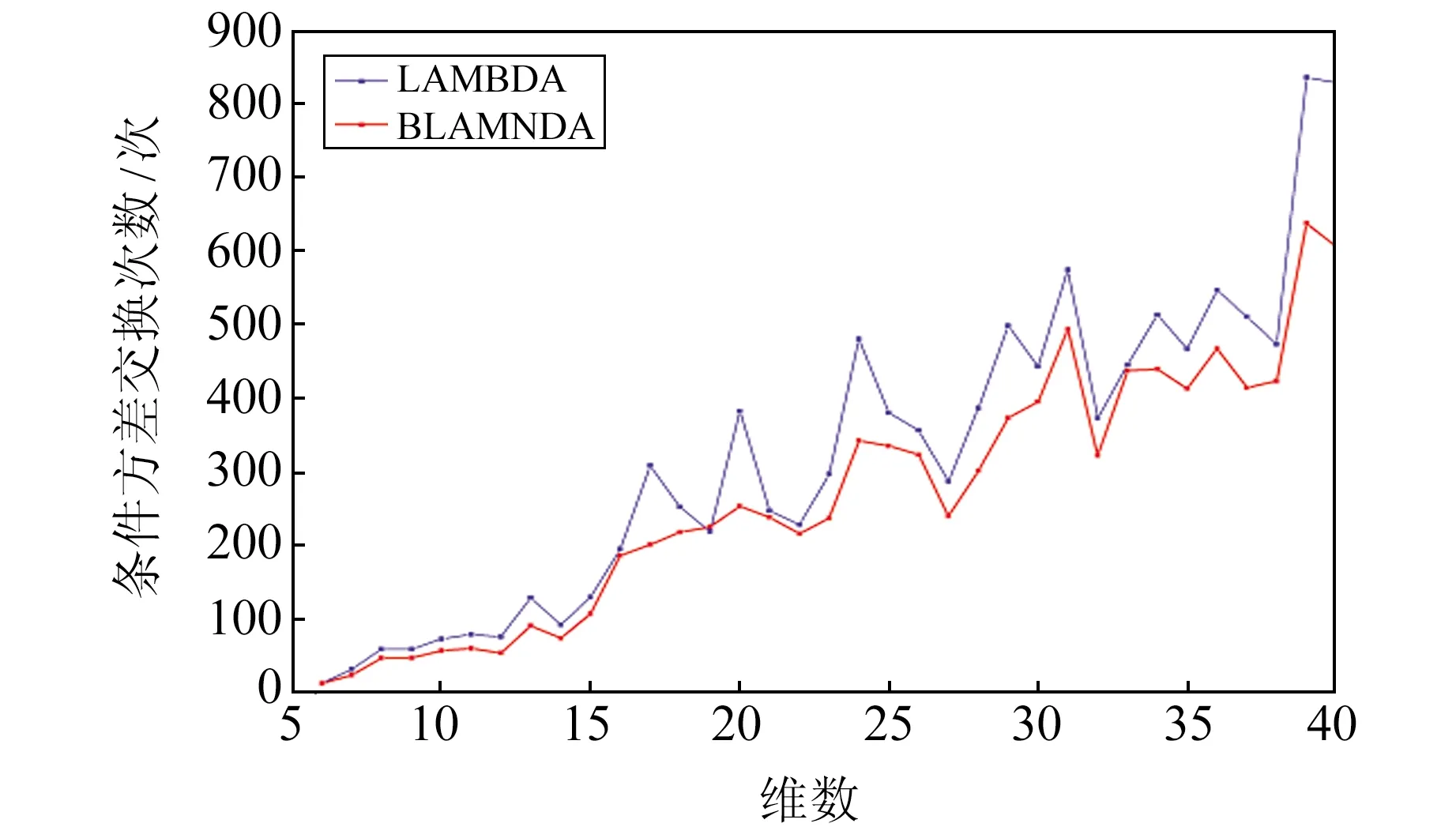
圖2 2種算法條件方差交換次數對比Fig.2 Comparison of conditional variance switching times between two algorithms

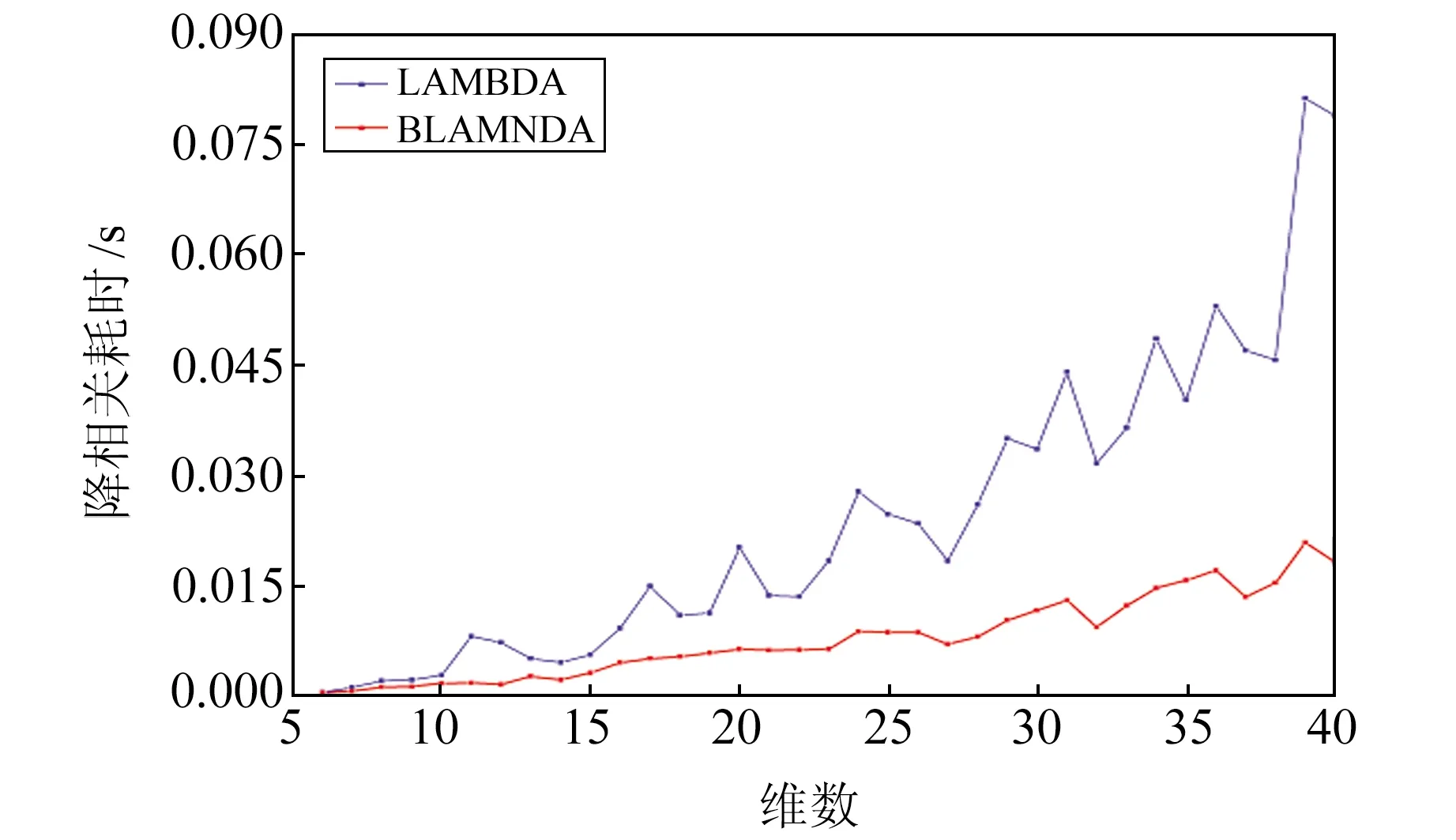
圖3 2種算法降相關耗時對比Fig.3 Time consumption of decorrelation of two algorithms

由圖1可見，LTDL分解算法具有可行性，說明減少矩陣的數乘可以明顯提高矩陣分解效率。由圖2可見，相較于LAMBDA算法，BLAMBDA分塊算法具有明顯的優越性。由圖3可見，總體上看，BLAMBDA算法在去相關耗時效率上優于LAMBDA算法。

3.2 實測實驗

實測實驗分為3組：1)短基線組采用1組和芯星通UB4B0-MINI板卡采集的靜態觀測數據，基線長89.83 m，采樣間隔為1 s，截取3 000個歷元進行實驗分析； 2)中長基線組采用武漢大學IGS數據中心下載的香港地區HKSL和HKWS測站的IGS數據，2站構成的基線長度為42.51 km，采樣間隔為30 s；3)長基線組采用武漢大學IGS數據中心下載的香港地區HKSL測站和上海SHAO測站的IGS數據，2站構成的基線長度為1 216.01 km，采樣間隔為30 s。本文所使用的數據包括星歷數據和觀測數據，且均為標準RINEX格式。為保證實驗的合理性，BLAMBDA算法和LAMBDA算法均采用SEVB搜索算法進行降相關處理[3]。本實驗基于RTKLIB的源代碼進行數據處理,實際解算過程中對2種算法的固定模糊度進行對比發現，二者結果一致性較高。本文提出的算法與RTKLIB源代碼中的LAMBDA算法具有一致性，在此基礎上采用GPS、BDS、Galileo、GLONASS等多系統數據進行整周模糊度融合解算，3種基線解算時間對比情況如圖4所示，耗時概率分布如圖5所示。

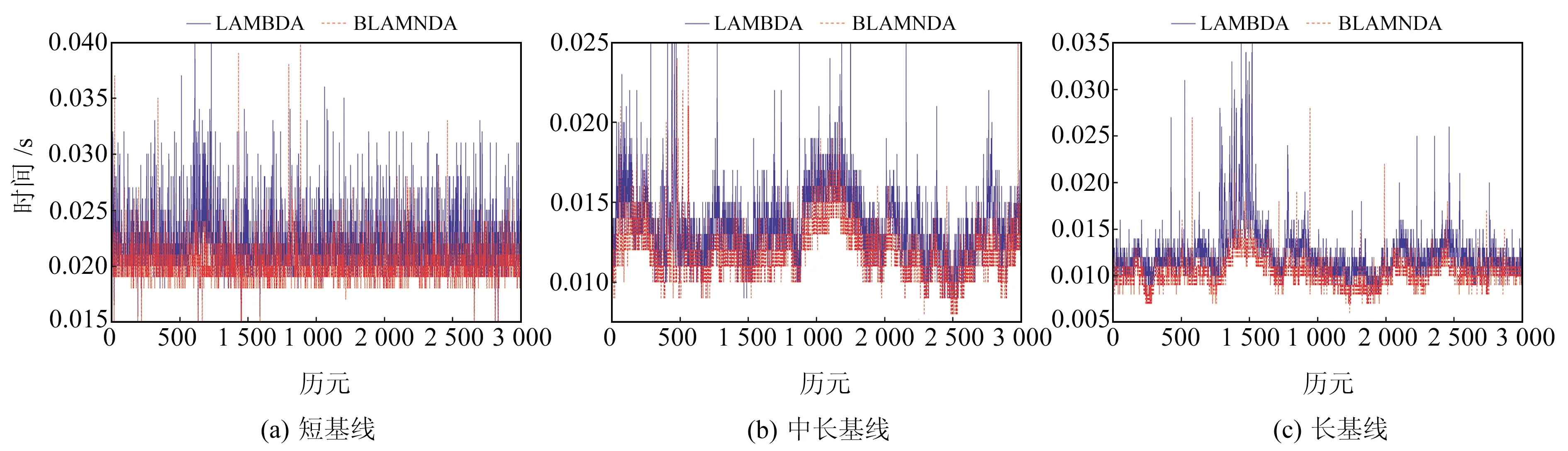
圖4 3種基線解算時間對比Fig.4 Comparison of three baseline calculation time

圖5 3種基線解算時間耗時概率對比分布Fig.5 Probability distribution of three baseline calculation time

由圖4可見，BLAMBDA算法的解算時間明顯短于LAMBDA算法。由于中長、長基線的采樣間隔為30 s，而短基線的時間間隔為1 s，中長、長基線的觀測時間長于短基線，因此圖4(a)的時間波動比圖4(b)、(c)的平緩。此外，短基線的雙差模糊度維數整體高于中長、長基線，雙差模糊度維數越高，BLAMBDA算法對時間效率的提升越明顯。

由圖5(a)可見，LAMBDA算法在0.021～0.035 s內的解算耗時概率明顯高于BLAMBDA算法，BLAMBDA算法的解算耗時大都集中在0.020 s左右；由圖5(b)、(c)可見，中長基線和長基線的BLAMBDA算法解算耗時與LAMBDA算法相比方差較小，解算耗時分布更加集中。LAMBDA算法存在高耗時的現象，而BLAMBDA算法在某種程度上彌補了這一缺陷。由此可以看出，BLAMBDA算法不僅在解算效率上優于LAMBDA算法，而且具有更好的穩定性。

4 結 語

為解決LAMBDA算法模糊度去相關過程計算量過大的問題，引入條件方差矩陣分塊方法，并對分解算法進行改進，提出BLAMBDA算法。仿真與實測實驗結果表明，BLAMBDA算法求解模糊度的整體效率高于LAMBDA算法。各歷元解算耗時大小的概率分布表明，BLAMBDA算法的計算穩定性優于LAMBDA算法。

在BLAMBDA算法中，對條件方差矩陣進行分塊處理，可以進一步提高模糊度的解算效率，這將是BLAMBDA算法下一步的研究重點。