考慮VSC-HVDC作用的LCC-HVDC系統短路比實用計算

楊曉雷，韓中杰，葉 琳，江俊賢，王奕鑫，王冠中

（1.國網浙江省電力有限公司嘉興供電公司，浙江 嘉興 314000；2.國網浙江省電力有限公司，杭州 310007；3.浙江大學 工程師學院，杭州 310027；4.浙江大學 電氣工程學院，杭州 310027）

0 引言

LCC-HVDC（電網換相換流器型高壓直流輸電）與VSC-HVDC（電壓源換流器型高壓直流輸電）饋入同一受端電網［1-3］。所形成的混合直流饋入系統已成為我國新型電力系統的代表模式之一［4-5］。交直流系統的相互作用［6］深刻影響受端電網的安全穩定運行，因此準確量化電網強度［7-8］，反映交直流相互作用程度，對于電網規劃和運行是非常重要的。

文獻［9］通過三階雅克比矩陣的奇異性分析LCC-HVDC單饋入系統功傳輸極限與電網強度的關系。文獻［10］基于模態解耦，利用特征值解耦的思路提出廣義短路比的指標，以此表征LCCHVDC 多饋入系統的電網強度。文獻［11］基于阻抗等值，將LCC-HVDC、VSC-HVDC 混合雙饋入系統等效成LCC-HVDC 單饋入系統，提出了HEESCR（混合饋入等效有效短路比）。文獻［12］考慮了VSC-HVDC對LCC-HVDC等值臨界阻抗的影響，類比LCC-HVDC 單饋入ESCR（有效短路比）指標，提出了EESCR（等值有效短路比）指標。綜合上述研究，文獻［9-10］僅研究了LCCHVDC 多饋入系統的電網強度作用機理；在混合直流饋入系統的電網強度與傳輸極限方面，文獻［11-12］均通過將VSC 進行阻抗等值，在此基礎上修正傳統LCC-HVDC 單饋入系統的電網強度指標，缺乏關于指標作用機理以及指標臨界值性質方面的深入分析［13］，導致難以形成混合直流饋入系統中電網強度的物理認識。

針對上述問題，本文首先根據交直流系統準穩態模型建立了LCC-HVDC和VSC-HVDC混合直流饋入系統的交流側與直流側的雅克比矩陣。其次，結合矩陣變換，通過降階雅克比矩陣奇異表征LCC-HVDC 功率傳輸極限，得到系統位于臨界穩定時的判斷條件；進一步類比傳統直流單饋入系統電網強度判據，得到適用于評估混合直流饋入中LCC-HVDC 系統靜態電壓穩定性的短路比指標及其臨界值，并說明在VSC-HVDC 的實際運行范圍內，系統的穩定裕度與VSC 運行方式存在明確的顯函數關系，因此能夠通過短路比指標有效評估系統的電壓穩定裕度。最后，通過PSCAD/EMTDC及MATLAB仿真算例驗證了所提分析方法的可行性和有效性。

1 混合直流饋入系統準穩態模型

圖1 為LCC-HVDC 和VSC-HVDC 雙饋入系統的拓撲結構，其中，Pd1和Pd2分別表示LCCHVDC 及VSC-HVDC輸送的有功功率；Qd1和Qd2分別為兩回直流注入交流電網的無功功率；Id1和Id2分別表示LCC-HVDC 及VSC-HVDC 輸送的電流；P1、P2、Q1、Q2分別表示交流網絡饋入的有功和無功功率；b10和b20表示交流系統的戴維南等值導納，b12為換流站間聯絡線導納；U1∠θ1和U2∠θ2分別表示換流站交流母線電壓幅值和相角；Bc1表示無功補償裝置的等值導納；E1和E2表示交流系統的等值內電勢。

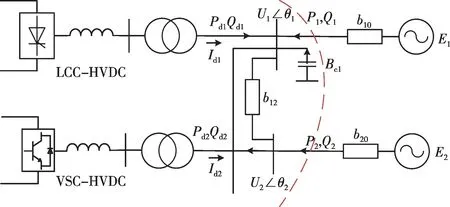
圖1 LCC-HVDC、VSC-HVDC混合饋入系統Fig.1 Dual-infeed HVDC system of LCC-HVDC and VSCHVDC

以下用U0∠θ0統一表示無窮大電網電壓（即忽略E1和E2之間的相角差）。系統潮流方程表示為：

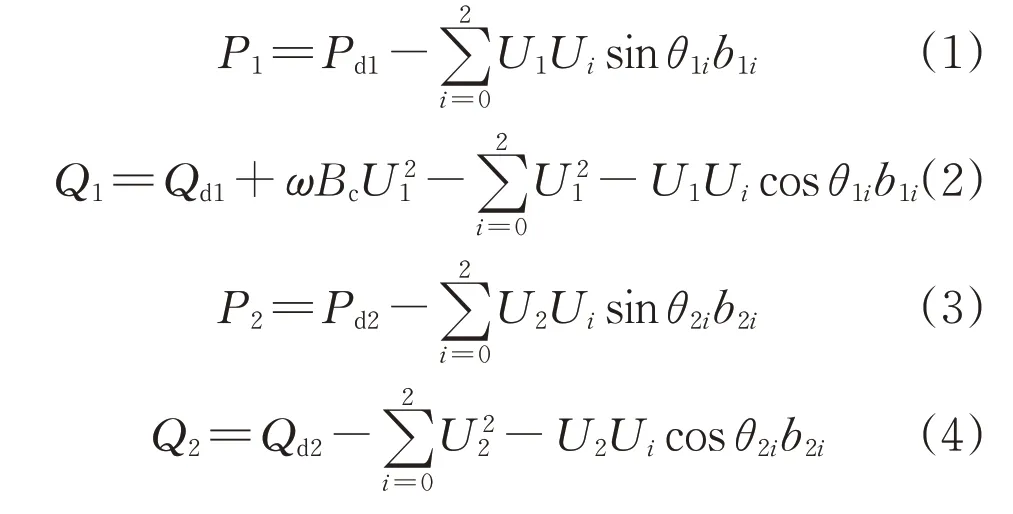
式中：bij和θij分別表示節點i和j之間的等值電納及電壓相角差、方程式（1）—（4）表征系統的交直流系統耦合特性。

2 混合饋入系統雅可比矩陣

基于LCC-HVDC和VSC-HVDC端口特性以及交流網絡的耦合，推導混合直流饋入系統的降階雅克比矩陣以及相應的臨界穩定條件。

2.1 LCC-HVDC單饋入系統的雅可比矩陣

首先建立LCC-HVDC系統在CP-CEA（定功率定熄弧角）和CC-CEA（定電流定熄弧角）兩種控制方式下的降階雅克比矩陣，并通過矩陣奇異條件分析功率傳輸極限。

CP-CEA/CC-CEA 控制方式下的LCCHVDC均通過增加直流電流來提高直流輸送功率，該控制功能的實現基礎為傳輸功率與電流存在正反饋關系。據此，文獻［4］給出了系統功率傳輸極限的定義：當增加電流時，傳輸功率不增反降，即認為直流已達傳輸極限，此時直流功率失去可控性。

本文在LCC-HVDC準穩態方程組［8］基礎上采用文獻［9］中的標幺化方法建立標幺值模型。LCC-HVDC設備側端口特性方程為：

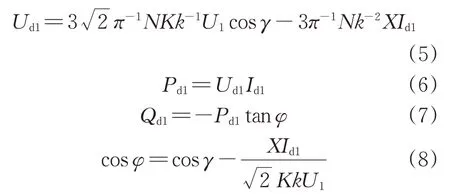
式中：Ud1表示LCC-HVDC 直流電壓；γ表示關斷角；X表示換向電抗大小；φ表征功率因數角；k為直流側電壓基準值與交流測電壓基準值的比值；K為變壓器變比。

文獻［14］提出以三階雅克比矩陣奇異作為LCC-HVDC的傳輸極限判據，即以電流、功角和交流電壓的微增量ΔId、Δθ和ΔU作為自變量，以直流傳輸功率、節點注入有功和無功功率的微增量ΔPd1、ΔP1和ΔQ1作為因變量建立的狀態雅克比矩陣表征系統的功率傳輸特性［15］（對CP-CEA 而言，當研究對象為直流傳輸功率與電流的關系時，不能令ΔPd1=0）。考慮CP-CEA/CC-CEA 控制方式下，針對LCC-HVDC 饋入系統的功率穩定問題，所對應的三階雅克比矩陣JPB如式（9）所示：

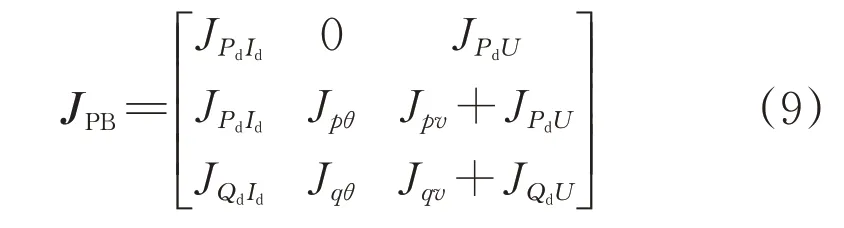
式中：JPdId等符號皆為下標對應的直流側/交流測變量之間的偏導數。

由于JPdId≠0，式（9）中的三階雅克比矩陣奇異性等價于降階雅可比矩陣JLCC+JAC的奇異性：

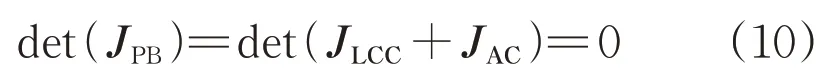
其中，JLCC代表直流側雅可比矩陣：

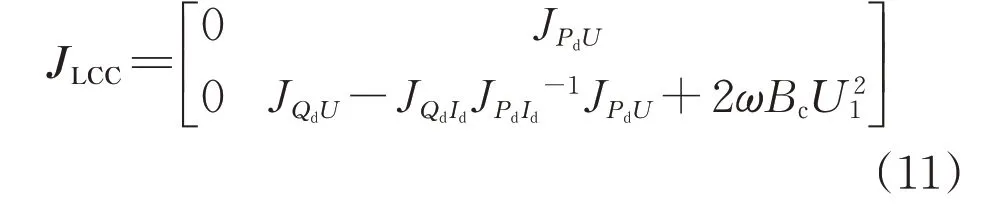
JAC表示交流雅可比矩陣，對應潮流方程線性化結果，具體表示為：

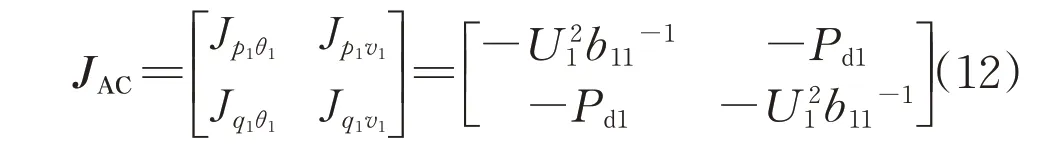
CP-CEA和CC-CEA兩種控制方式均在矩陣JPB奇異的條件下到達直流傳輸極限［6，10］，對應的臨界短路比約為2［15］。

2.2 VSC-HVDC直流側雅可比矩陣

VSC-HVDC考慮不同控制方式的雅可比矩陣元素分別為：

1）定功率控制方式

考慮VSC-HVDC 定功率控制方式下，直流設備側雅可比矩陣滿足［18］：

2）定交流電壓控制方式

考慮VSC-HVDC 定交流電壓控制方式下，對應設備側雅可比矩陣滿足：

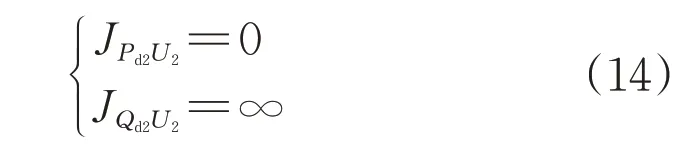
綜合上述兩種控制方式，VSC-HVDC直流側雅可比矩陣可統一表示為：

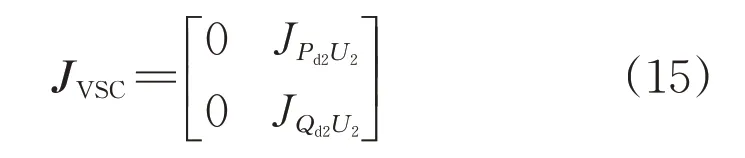
2.3 混合饋入系統的雅可比矩陣

根據前面兩節的內容，可將混合饋入系統的雅克比矩陣簡單表示如下：

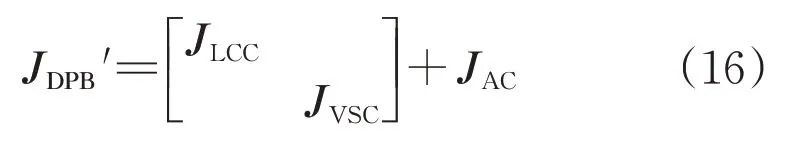
3 混合直流饋入系統短路比計算方法

3.1 短路比指標的定義

根據圖1所示拓撲，定義混合直流饋入系統中用于評估傳輸極限的SCR（短路比）指標表示為：

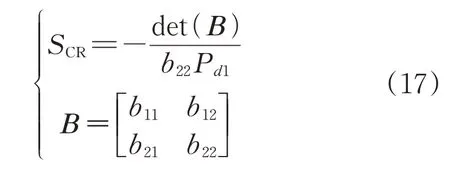
式中：det(B)表示導納矩陣的行列式，det(B)/b22表征VSC-HVDC 接入后交流網絡的修正等值導納，物理上代表將VSC-HVDC 外部電路折算到LCC-HVDC單饋入系統中的結果。折算過程如圖2 所示，根據工程中VSC-HVDC 容量較之LCCHVDC 要小很多，其對電網強度的影響也遠小于LCC-HVDC，故在圖2 中用虛線表示等效過程前的VSC-HVDC 并在電路折算中忽略其影響。值得說明的是，當忽略混合饋入系統中的VSCHVDC 以及與之相關的交流線路時，式（17）中的短路比指標化簡為-b10/Pd1，等于LCC-HVDC單饋入系統SCR。

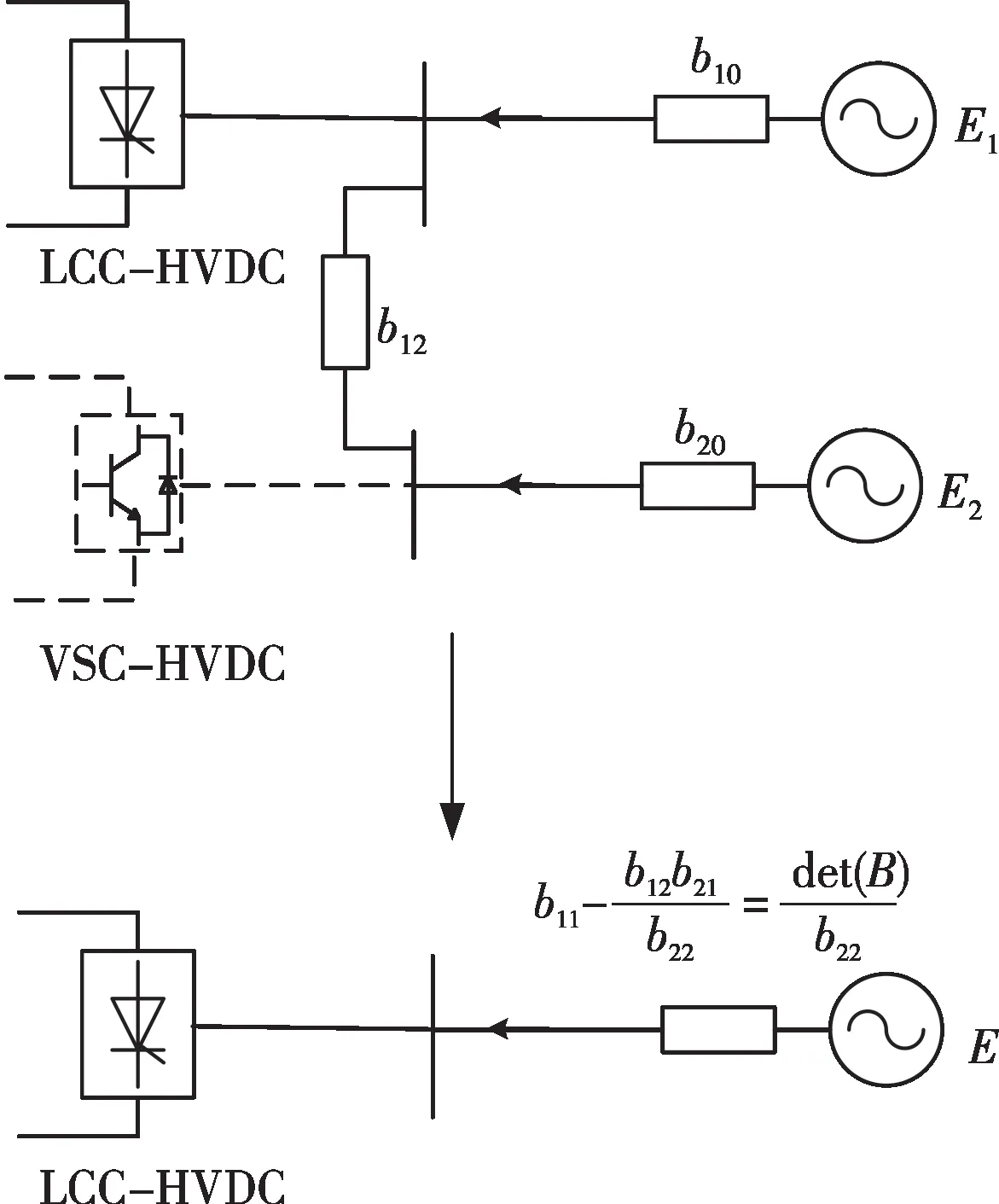
圖2 SCR指標對應的外部電路過程示意圖Fig.2 Schematic diagram of the external circuit process corresponding to the SCR indicator

所提指標的有效性可通過對2.3節中矩陣奇異所代表的臨界穩定條件進行說明。

1）VSC-HVDC定功率控制方式

系統臨界穩定時，對應式det(JDPB′)=0：

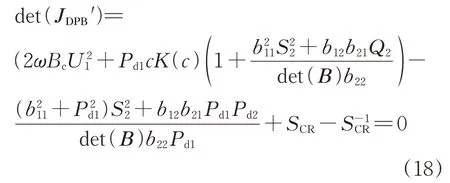
式中：bij表示節點i與節點j之間的互導納。

觀察式（18）可知，該臨界穩定條件類似LCCHVDC單饋入系統的臨界穩定條件［10］，即

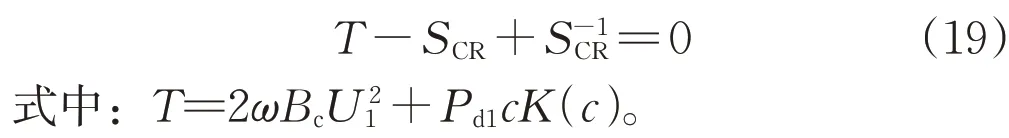
結合式（19）可得考慮VSC-HVDC 定功率控制方式下，混合直流饋入系統對應的修正參數T′為：

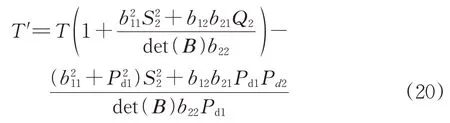
進一步整理可得臨界短路比CSCR為［10］：

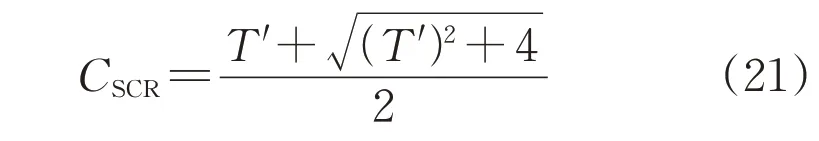
2）VSC-HVDC定交流電壓控制方式

臨界穩定條件為式（22）所示，其對應式（16）刪去JQd2U2元素所在行列并計算行列式的結果：

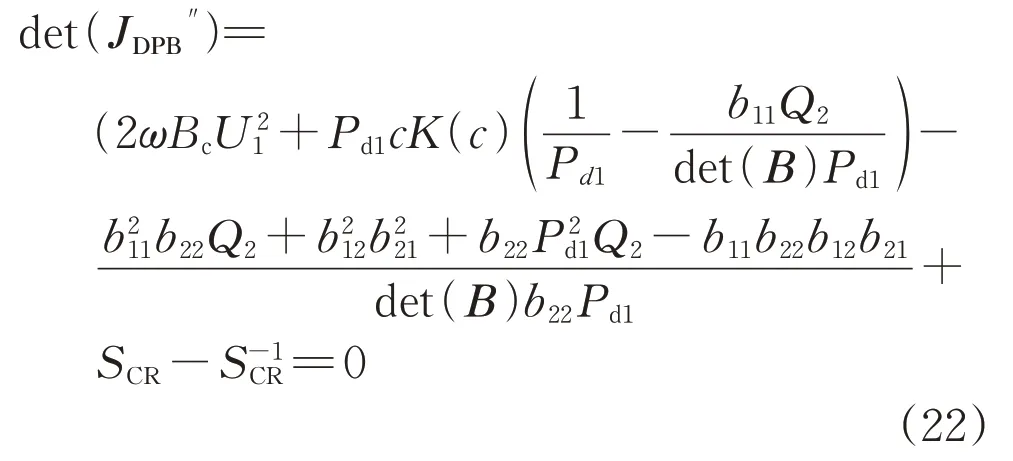
由式（22）可知，考慮VSC-HVDC 定電壓控制方式下，混合直流饋入系統的修正參數T″為：

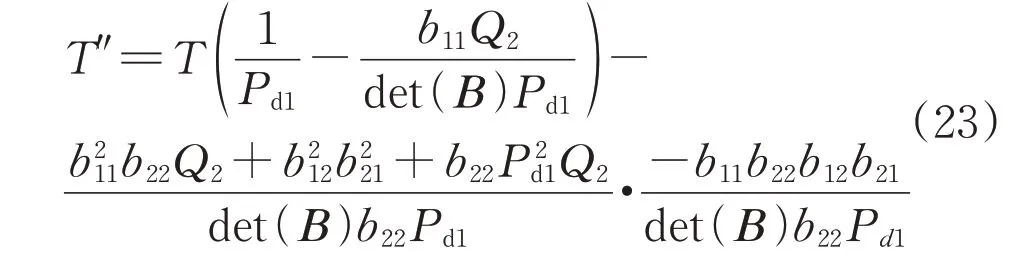
該控制方式下的CSCR 為把式（23）得到的修正參數代入式（21）的結果。

當混合直流饋入系統的SCR下降到CSCR時，系統額定運行功率與傳輸極限重合。當SCR 小于CSCR 時，LCC-HVDC 無法達到額定運行功率；當SCR 大于CSCR 時，LCC-HVDC 額定運行功率未達到傳輸極限。考慮額定運行工況下，定電圧控制方式下的CSCR 相較定功率控制方式下的CSCR較小，即VSC-HVDC定交流電壓控制方式相較定功率控制方式而言，對LCC-HVDC 傳輸功率具有更大的支撐強度。

CIGRE 標準直流系統的典型參數T約等于1.5［10］，而對于本文中的修正參數受VSC-HVDC注入功率的影響，進而影響CSCR 的數值，下文將具體分析影響的性質與大小。

3.2 臨界值的靈敏度分析

分析VSC-HVDC 運行方式對系統穩定裕度的影響。考慮規劃階段VSC-HVDC 的容量視為常量，將CSCR分別對Pd2與Qd2求偏導可得：

1）VSC-HVDC定功率控制

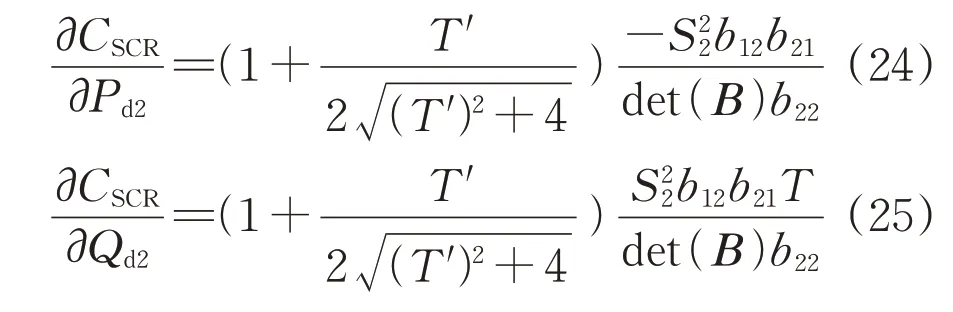
考慮直流饋入系統的導納矩陣為對角線占優的負定矩陣［10］，自導納b22＜0，det(B)＞0，式（24）、式（25）滿足：

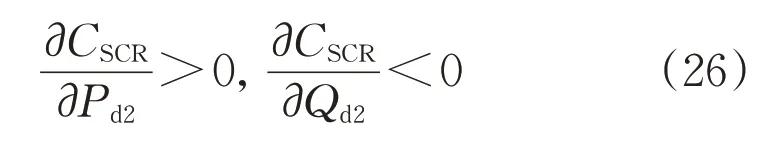
2）VSC-HVDC定電壓控制方式

基于推導得到的功率分岔雅克比矩陣中不含Pd2元素，即Pd2對臨界短路比影響較小，由式（26）可得：

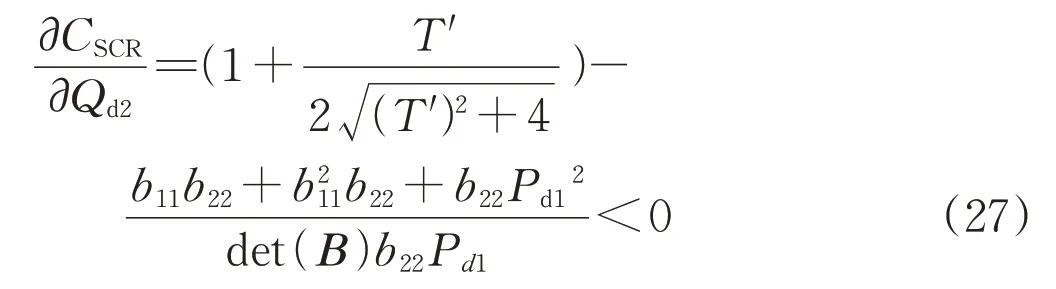
基于式（24）與式（25）的分析結果可知，隨著VSC-HVDC 輸出的無功功率的增大，T′、T″減小，CSCR 也越小，SCR-CSCR 增大，系統穩定裕度越大；VSC-HVDC 輸出的有功功率越大，CSCR 也越大，SCR-CSCR 減小，系統穩定裕度越小。

基于混合直流雙饋入系統提出的SCR 機理未來可拓展于多饋入系統。針對混合多饋入系統的電網強度評估，可拓展本文中的穩定機理以及影響因素作用關系。具體地，多饋入系統中VSCHVDC 的注入功率對多饋入系統短路比臨界值的影響可以通過文獻［20］中的攝動法進行近似分析，然而，文獻［20］中的分析方法缺乏實際系統中的物理對象的支撐，僅是一種數值近似手段，未來將研究結構保持的多饋入系統的短路比作用機理以及準確量化該指標臨界值跟多饋入系統中VSC-HVDC運行方式以及網絡結構的關系。

4 算例分析

4.1 系統模型

本節旨在說明混合直流饋入系統中SCR 及CSCR 指標的有效性。基于PSCAD/EMTDC 與MATLAB仿真軟件搭建了如圖1所示的系統，其中LCC-HVDC 采用CIGRE 標準直流測試系統參數。表1 為LCC-HVDC 系統參數，表2 為采用定功率控制方式下VSC-HVDC的控制環節參數。

表1 LCC-HVDC系統參數Table 1 LCC-HVDC system parameters

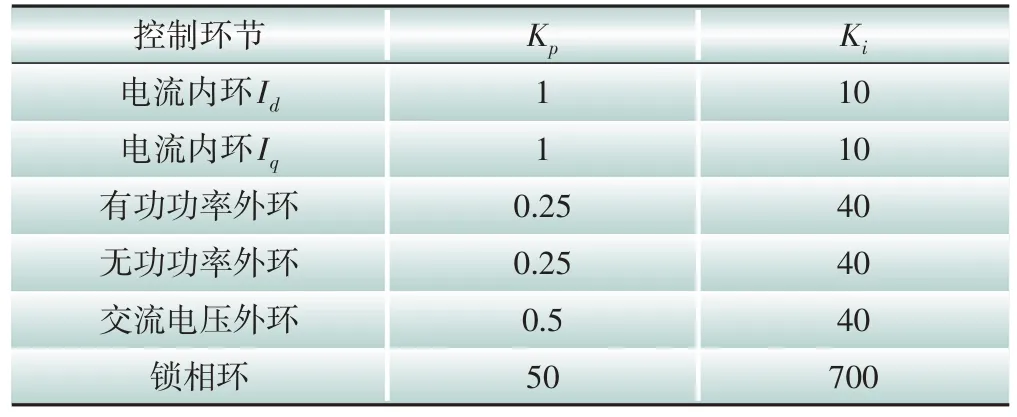
表2 VSC-HVDC控制環節參數Table 2 VSC-HVDC control link parameters

仿真中混合直流饋入系統的直流側額定功率為1 000 MW，直流側額定電壓500 kV，逆變側交流系統的額定電壓采用線電壓有效值230 kV，變壓器變比K=211.42/230，交直流電壓基準值的比例k=500/230。

4.2 所提指標有效性分析

首先驗證2.1 節中CP-CEA 及CC-CEA 兩種控制方式下LCC-HVDC 單饋入系統的臨界短路比的一致性。基于上文提到的CIGRE標準測試系統，在仿真中分別增大兩種控制方式下系統的網絡電感值直至系統到達臨界穩定。由仿真結果可得，CP-CEA 控制方式下，LCC-HVDC 單饋入臨界短路比為2.04；CC-CEA 控制方式下，LCC-HVDC單饋入系統的臨界短路比為2.06。即兩種控制方式下，LCC-HVDC單饋入系統的臨界短路比近似等于2。

以下說明本文提出的SCR 指標用于評估混合直流饋入系統中LCC-HVDC 傳輸極限的有效性。在仿真模型中控制LCC-HVDC 直流電流指令值以施加功率擾動，仿真中設置直流電流參考值每10 s 增加0.1 p.u.，通過對比不同穩定裕度下的LCC-HVDC功率傳輸曲線，說明LCC-HVDC功率傳輸極限與SCR-CSCR的關系。

仿真得到不同穩定裕度下，LCC-HVDC的直流功率傳輸特性曲線如圖3所示。保持仿真系統的SCR 為1.975 恒定，其中case1 表示VSC-HVDC不注入有功無功功率時Pd1隨Id1的變化曲線，即Pd2=0，Qd2=0 的運行方式，對應的CSCR=1.975=SCR；case2 表示VSC-HVDC 注入0.15 p.u.的Pd2和0.26 p.u.的Qd2，對應的CSCR=1.968＜SCR；case 3 曲線表示VSC-HVDC 注入0.3 p.u.Pd2的LCC-HVDC 的傳輸特性，對應的CSCR=1.984＞SCR；case 4曲線表示定交流電壓控制方式下VSCHVDC 不注入有功無功功率時LCC-HVDC 的傳輸特性，對應的CSCR=1.984＜SCR。由圖3 case1曲線可知，當SCR=CSCR時，Pd1最大傳輸功率為1.008 p.u.，最大傳輸功率對應的Id1為1.012 p.u.，系統的額定運行功率與傳輸極限近似相等；根據SCR＜CSCR對應的case3曲線可知，系統的最大傳輸功率0.96 p.u.，對應的直流電流Id1為0.92 p.u.，系統在額定點無法穩定運行，傳輸極限小于額定功率；根據SCR＞CSCR對應的case2曲線可知，系統傳輸功率極限為1.08 p.u.大于額定功率，Id1為1.13 p.u.，case3相較case2 VSC-HVDC向換流母線注入更多無功功率，SCR 與CSCR 的差變大，電網強度變大，在系統額定運行點尚未達到功率傳輸極限，具有一定的穩定裕度。由case 4對應的仿真結果可知，VSC-HVDC定電圧控制方式相較于定功率控制方式對LCC-HVDC具有更好的支撐能力。

圖3 不同穩定裕度下，LCC-HVDC的傳輸特性曲線Fig.3 Transmission characteristic curve of LCC-HVDC under different stability margins

上述分析驗證了本文提出的CSCR 指標用于評估混合直流饋入系統中LCC-HVDC 傳輸極限的有效性。SCR=CSCR為系統的臨界穩定條件，此時額定運行點與傳輸極限點重合。此外，通過SCR與CSCR的差能夠表征系統穩定裕度。

4.3 SCR指標臨界值的數值誤差分析

本節說明考慮VSC-HVDC 的運行方式后，本文提出的SCR 指標的臨界值相較其他指標具有更小數值偏差。

計算VSC-HVDC 額定容量為0.5 p.u.時，不同運行方式下的CSCR。仿真得到的CSCR 隨VSC-HVDC 注入換流母線功率變化的曲面如圖4所示。由圖4可知，考慮VSC-HVDC運行方式后仿真得到的CSCR在1.94～2.04區間內，與單饋入LCC-HVDC 的SCR 指標在CIGRE 標準直流系統典型參數下對應的臨界值2非常接近，最大數值誤差為3%。

圖4 臨界短路比隨VSC-HVDC注入功率變化范圍曲面Fig.4 Critical revised short-circuit ratio varies with the injected power of VSC-HVDC

進一步地，將SCR 與文獻［12］和［19］中的EESCR 指標及文獻［22］的MIESCR（多饋入有效短路比）指標進行比較，以說明本文所提指標具有更小的數值計算誤差。EESCR的定義為［12］：

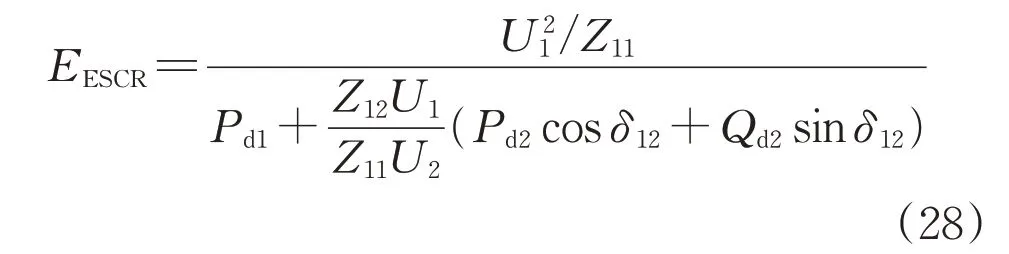
式中：Zij表示節點i與節點j間的等效阻抗。

MIESCR指標的定義表示為［21］：

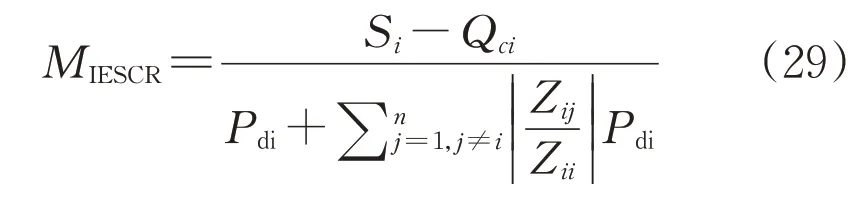
式中：Si表示換流母線i的短路容量；Qci表示母線i的無功補償量；節點j間的等效阻抗。

基于文獻［19］表5的算例，對SCR、MIESCR及EESCR指標臨界值進行誤差分析，利用仿真得到計算臨界值并與其對應的理論臨界值計算相對誤差，結果如表3 所示。由表3 可知，考慮VSCHVDC 對CSCR 的影響不大，臨界值仍接近于2，而VSC-HVDC注入換流母線的功率會影響LCCHVDC 的傳輸功率極限，從而對MIESCR/EESCR等通過功率等值法得到的短路比指標的臨界值造成比較大的數值偏差。CSCR在不同VSCHVDC 運行方式下的變化范圍較小，且相較現有的混合直流饋入系統強度評估指標而言，本文所提短路比指標的相對數值誤差較小。

表3 指標臨界值數值相對誤差分析Table 3 Analysis of relative error of index critical numerical value

5 結語

為探究直流饋入系統中VSC-HVDC 接入對LCC-HVDC傳輸極限的影響，本文基于降階雅克比矩陣，對現有LCC-HVDC單饋入短路比指標進行修正，得到了適用于評估混合直流饋入中LCCHVDC 系統穩定性的SCR 指標。數學上，所提SCR與混合直流饋入系統中LCC-HVDC的傳輸極限有著明晰的顯函數關系，能夠有效量化混合直流饋入系統的靜態電壓穩定裕度；物理機理上，所提SCR 對應VSC-HVDC 外部電路折算到LCCHVDC交流網絡側的結果。具體分析結果如下：

1）比較了VSC-HVDC 不同運行與控制方式下LCC-HVDC 系統的臨界短路比，分析結果表明VSC-HVDC 注入功率對CSCR 影響較小，且VSC-HVDC 在定電壓控制方式下更有利于支撐LCC-HVDC的傳輸功率。

2）基于PSCAD/EMTDC及MATLAB平臺給出算例分析，驗證了本文提出的短路比指標的有效性。仿真結果表明所提指標的臨界值CSCR 相較于現有基于電路等值思想量化混合饋入系統強度的評估指標具有更小的數值誤差。