加權總體最小二乘和RBF神經網絡的三維坐標轉換

趙 輝 郭春喜 孟靜娟 耿曉燕 王文超

1 自然資源部大地測量數據處理中心，西安市友誼東路334號，710054

大地測量中不同大地坐標系間的轉換可通過三維七參數模型實現：選擇一定數量且分布較為均勻的公共點數據求取坐標轉換參數，建立坐標系間的轉換關系。通常基于最小二乘原理，以轉換殘差加權平方和最小為目標條件進行平差計算。由于2000國家大地坐標系的精度比傳統參心坐標系高1～2個數量級[1]，因此對已有參心坐標系成果進行轉換時，需要考慮參心坐標系下坐標成果存在的誤差。

總體最小二乘法(TLS)能夠求解受隨機誤差影響的變量誤差模型(EIV)，由于系數矩陣中各隨機元素的精度不同，因此TLS可進一步擴展為加權總體最小二乘法(WTLS)。WTLS常用的求解方法是基于拉格朗日乘數法的條件極值建立的迭代算法[2]。目前，WTLS方法已被廣泛應用于坐標轉換、高程擬合、線性回歸等[3-5]。由于EIV模型假定系數矩陣中每個元素都存在誤差，而三維七參數轉換模型的系數矩陣中存在常數項，因此可設置系數矩陣協因數陣相應元素為0，進而使常數項元素改正數為0。但上述方法無法解決系數矩陣中存在重復元素的問題。部分變量誤差模型(Partial EIV)對EIV模型進行了擴展，使得系數矩陣中部分元素存在誤差，進而形成統一的模型形式[6]。

采用Partial EIV模型的加權總體最小二乘法WTLS能夠提高三維七參數的精度，但在對參數進行轉換時，待轉換坐標的誤差是未知的。基于此，本文采用RBF神經網絡建立源坐標系坐標的誤差分布模型，從而更有效地發揮七參數加權總體最小二乘解的作用。

1 三維坐標轉換的加權總體最小二乘法WTLS

1.1 三維坐標轉換模型

不同空間直角坐標系轉換的布爾莎模型為：

(1)

式中，(XS,YS,ZS)為源坐標系下的坐標，(XT,YT,ZT)為目標坐標系下的坐標，ΔX0、ΔY0、ΔZ0為3個平移參數，εX、εY、εZ為3個旋轉參數，m為尺度參數。

令a1=m+1、a2=a1εX、a3=a1εY、a4=a1εZ，則式(1)可改寫為：

(2)

式中，n為控制點個數。

(3)

式中，x0為參數近似值，Qy為觀測值向量協因數陣。

1.2 Partial EIV模型的加權總體最小二乘法

考慮到系數矩陣受隨機誤差影響，且存在非隨機元素或重復隨機元素，需采用Partial EIV模型[6]：

(4)

(5)

其中，Qa為系數向量a的協因數陣。

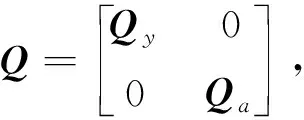
1)設置初值：x(0)=xLS，ea(0)=0。

三維坐標轉換的Partial EIV模型中，向量h和固定矩陣B為[9]：

(6)

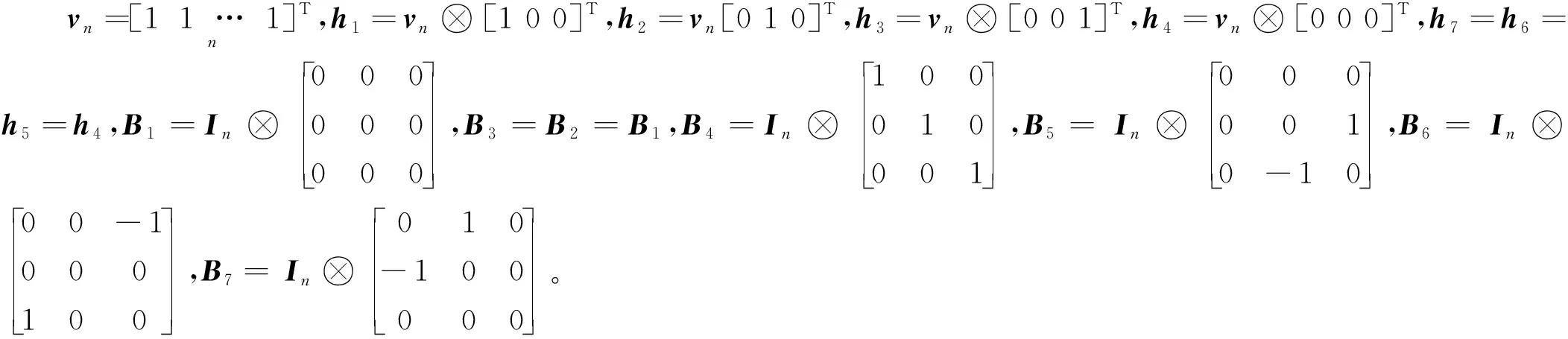
2 顧及源坐標系坐標誤差的RBF組合解法

2.1 RBF神經網絡

RBF神經網絡是一種3層前饋局部逼近網絡，將輸入層數據非線性變化到高維空間的隱含層中，實現低維度空間內線性不可分問題在高維度空間內的線性可分，再將隱含層線性變換到輸出層中[10]。

通常選用高斯函數作為徑向基函數的激活函數：

(7)

式中，φj(X)為隱含層第j個神經元的輸出值，X為輸入向量，μj為隱含層神經元中心參數，σj為高斯函數的擴展參數。

輸出層估計值為：

(8)

式中，wkj為輸出層第k個神經元與隱含層第j個神經元之間的權重。

對于坐標改正數，可建立隱含層有m個神經元的(3×m×3)神經網絡。

2.2 組合解法的建立

使用Partial EIV模型的加權總體最小二乘法求解三維坐標轉換參數，在考慮系數矩陣誤差的情況下，求出七參數以及源坐標的改正數。由于使用七參數進行轉換時無法確定待轉換坐標的誤差大小，因此本文基于RBF神經網絡建立源坐標的誤差分布模型，從而更有效地發揮加權總體最小二乘法對七參數求解的作用。

具體流程如圖1所示，算法步驟如下：

1)根據§1.1中公式，利用重合點坐標計算七參數加權最小二乘解，并將其作為初值；

2)根據§1.2中迭代過程計算Partial EIV模型的加權總體最小二乘解；

3)利用步驟2)計算出的源坐標系坐標改正數訓練RBF神經網絡；

4)基于RBF神經網絡計算的待轉換點坐標改正數，利用Partial EIV模型的加權總體最小二乘法求出的七參數進行轉換。

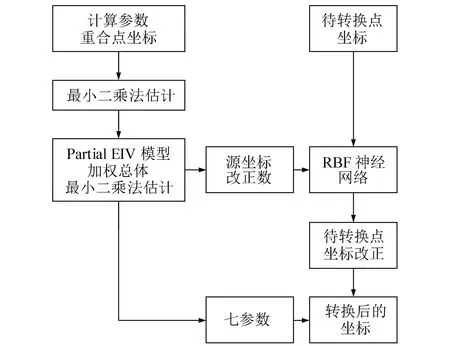
圖1 組合方法坐標轉換流程Fig.1 Coordinate transformation process of composite method

3 實驗分析

本文選取某地81個同時具有1980西安坐標系和2000國家大地坐標系成果坐標的重合點數據，利用其中69個點計算模型參數，12個點作為檢核點，分別計算最小二乘解LS、加權總體最小二乘解WTLS、Partial EIV模型的加權總體最小二乘解PWTLS，并檢驗本文提出的PWTLS+RBF組合方法的有效性。

表1(單位m)為3種七參數解算模型的單位權中誤差，可以看出，相比于經典最小二乘平差LS，考慮系數矩陣中存在誤差的WTLS單位權中誤差提高了29%，考慮系數矩陣中存在相關元素的PWTLS單位權中誤差提高了55%。

表1 單位權中誤差

表2(單位m)為3種求解參數方法的內符合精度，可以看出，PWTLS的內符合精度略高于LS，但低于WTLS。這是因為WTLS未考慮系數矩陣中的重復元素，所以能夠自由調節改正數以滿足目標函數。

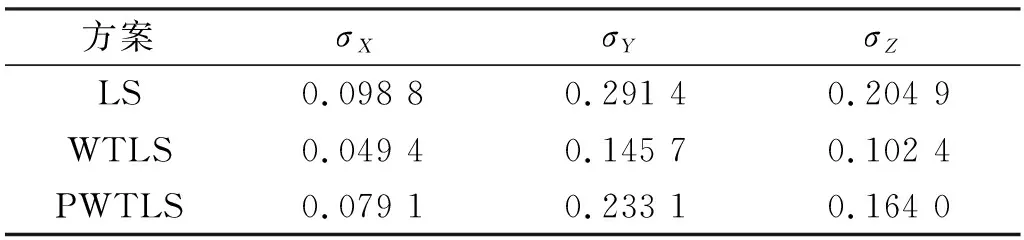
表2 內符合精度比較

表3(單位m)為3種方法的外符合精度比較，由表可見，3種方法的外符合精度均相同，這主要是因為3種方法求出的七參數值差異較小，所以在未知檢核點坐標誤差的情況下，求解出的轉換殘差基本相同。而本文提出的PWTLS+RBF組合方法首先利用RBF神經網絡計算檢核點的坐標誤差，然后根據PWTLS方法計算的轉換參數進行轉換，因此外符合精度較高。

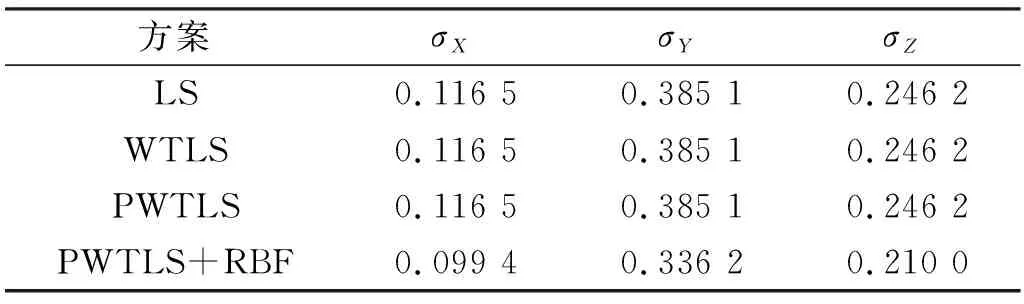
表3 外符合精度比較

圖2(a)、(b)為PWTLS方法直接解算得到的參數點源坐標改正數，以此為訓練樣本對RBF神經網絡進行訓練；圖2(c)、(d)為利用訓練完成的RBF神經網絡檢核點源坐標改正數，對源坐標進行改正后再根據七參數進行轉換的過程圖，轉換結果如圖3所示。

由圖3(a)、(b)可見，PWTLS+RBF組合法計算參數點高斯投影平面坐標殘差的絕對值小于0.1 m，大地高殘差的絕對值小于0.5 m；由圖3(c)、(d)可見，PWTLS+RBF組合法檢核點高斯投影平面坐標殘差的絕對值小于0.05 m，大地高殘差的絕對值小于0.5 m，說明重合點的大地高精度較低。

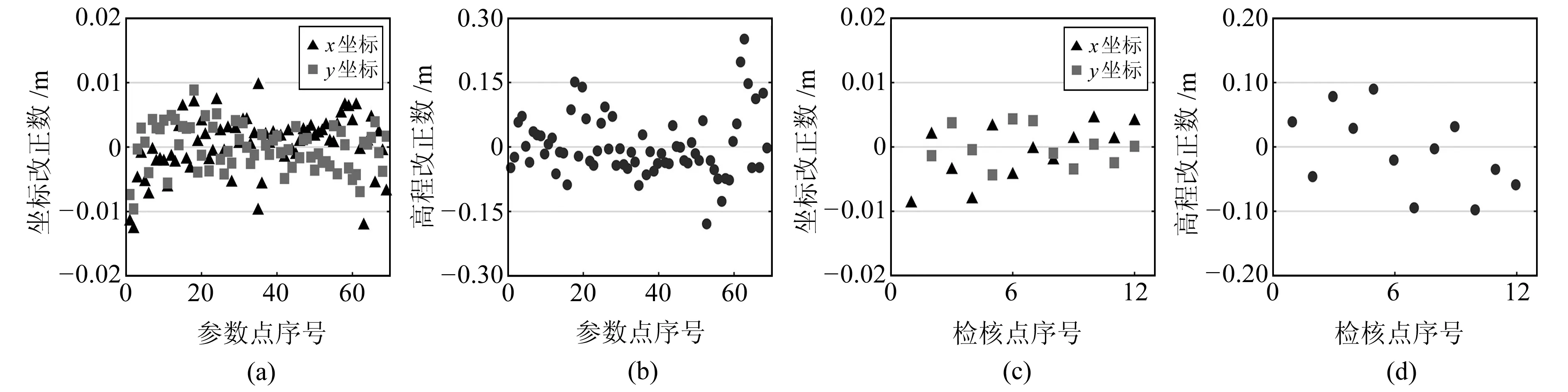
圖2 源坐標改正數Fig.2 Correction of source coordinate

圖3 PWTLS+RBF組合法轉換殘差Fig.3 Residuals of coordinate transformation method combining PWTLS and RBF

4 結 語

本文顧及源坐標誤差對轉換參數求解的影響，對比分析LS、WTLS、PWTLS方法對七參數求解的不同影響。為解決實際轉換過程中待轉換坐標誤差未知的問題，提出PWTLS+RBF組合坐標轉換方法。實驗結果表明，PWTLS能夠更好地解決轉換模型系數矩陣中同時存在常數元素和重復元素的問題，單位權中誤差和內符合精度均小于LS，且源坐標改正數較WTLS更加合理。PWTLS+RBF方法能夠使PWTLS求解參數得到有效使用，提高其在實際應用中的轉換精度。