基于改進灰狼算法的印刷包裝車間動態(tài)調(diào)度方法

彭來湖，萬璐璐，李建強，袁嫣紅，王偉華

(1.浙江理工大學，浙江 杭州 310000；2.浙江理工大學龍港研究院，浙江 溫州 325000；3.浙江大學，浙江 杭州 310000)

1 引言(Introduction)

隨著我國經(jīng)濟的發(fā)展，印刷包裝行業(yè)的社會需求日益增加，其對包裝、印刷技術等方面的需求越來越大[1]。大部分印刷包裝企業(yè)主要以“按需生產(chǎn)，零剩余產(chǎn)品”為目標制訂合理高效的生產(chǎn)計劃，從而提高生產(chǎn)效率和車間設備利用率。

近年來，研究車間動態(tài)調(diào)度的文獻逐漸增多[2-4]。匡鵬等[5]提出了一種將動態(tài)柔性作業(yè)車間調(diào)度問題中動態(tài)時間預測與遺傳模擬退火算法相結合的優(yōu)化調(diào)度方法。劉微等[6]針對動態(tài)作業(yè)車間中的機器故障、取消訂單、增加訂單和加急訂單的動態(tài)調(diào)度問題，以最短加工時間為優(yōu)化目標，提出了一種混合灰狼算法的動態(tài)作業(yè)車間調(diào)度技術，但是未考慮機器負荷和機器總能耗情況。張祥等[7]提出了一種考慮最大完工時間、機器負荷和機器總能耗等性能指標更加合理情況下的粒子群遺傳算法。

印刷包裝包括原材料供應、切紙、設計、制版、印刷、燙金、蓋光、壓痕、裝訂、打包、托運等多道工序分工協(xié)作，是典型的長流程型生產(chǎn)工藝。在生產(chǎn)過程中存在設備故障、緊急插單、交貨期變更、物料短缺等不確定因素，目前針對印刷包裝車間動態(tài)問題進行研究的文獻較少。

結合印刷包裝車間生產(chǎn)實際需求，綜合考慮機器故障和緊急訂單對正常生產(chǎn)的影響，本文設計了最大完工時間、機器負荷、機器總能耗為目標函數(shù)的多目標車間動態(tài)調(diào)度優(yōu)化模型，并提出了一種改進灰狼算法，以解決車間調(diào)度過程涉及大量人為主觀判斷而導致機器總能耗、訂單最大完工時間等無法保證的問題。

2 問題描述及建模(Problem description and modeling)

2.1 問題描述

表1 參數(shù)含義表Tab.1 Parameter meaning table

(續(xù)表)

2.2 問題建模

2.2.1 目標函數(shù)

為應對印刷包裝車間調(diào)度的需要，實現(xiàn)各個需求間的相互平衡，該印刷包裝車間調(diào)度模型設置了三個評價目標。

(1)最大完工時間最小化。最大完工時間指訂單的最后一道工序完成時間，最大完工時間(f1)可以宏觀反映車間生產(chǎn)狀況和車間的生產(chǎn)效率，如公式(1)所示：

(2)機器負荷平衡。機器負荷與機器利用率成反比，若要提高機器的利用率，則需使機器的負荷盡量小且平衡，如公式(2)所示：

(3)機器總能耗低。合理的調(diào)度方案不僅要考慮最大完工時間，還要綜合考慮車間機器總能耗。在最大完工時間一樣的情況下，合理選擇機器，使機器總能耗最低，如公式(3)所示：

2.2.2 約束條件

印刷包裝車間調(diào)度問題的約束條件如下。

(1)同一時刻、同一臺機器只能加工一個工件，同一時刻、同一工件只能在同一機器上加工。

(2)不同訂單的不同工序之間不存在順序約束，但同一訂單的不同工序存在順序約束，并且不同訂單的同一工序之間不存在優(yōu)先級約束。

(3)每臺機器和每個工件具有相同的優(yōu)先級，工件一旦開始加工，除非機器發(fā)生故障，否則不能中斷加工過程。

(4)不同工序的準備時間可忽略不計。

3 改進灰狼算法設計(Design of improved Grey Wolf algorithm)

MIRJALILI等[8]提出了灰狼算法，它是由灰狼群體捕食機制演化而來的元啟發(fā)式算法。與其他智能算法相比，該算法設計簡單，并且具有設置初始參數(shù)少、求解精度高等優(yōu)點，受到了學者的廣泛關注[9-11]，廣泛地應用于車間調(diào)度等領域。與此同時，該算法存在種群多樣性差、后期收斂速度慢、易陷入局部最優(yōu)的缺點。因此，可以采用混合策略方法初始化、NSGAII方法更新決策層個體位置、局部搜索及精英反向?qū)W習策略的方法改進灰狼算法，以提高算法的收斂性與分布性。

3.1 編碼與解碼機制

本文采用一種數(shù)字編碼的方法求解具有機器故障和緊急訂單的印刷包裝車間調(diào)度問題。編碼包含兩個部分：機器選擇和工序排序。

(1)機器選擇：每個基因都用一個數(shù)字表示當前的工序在可用機器中選擇的順序號，每個數(shù)字根據(jù)工序的加工順序依次排列(圖1)。

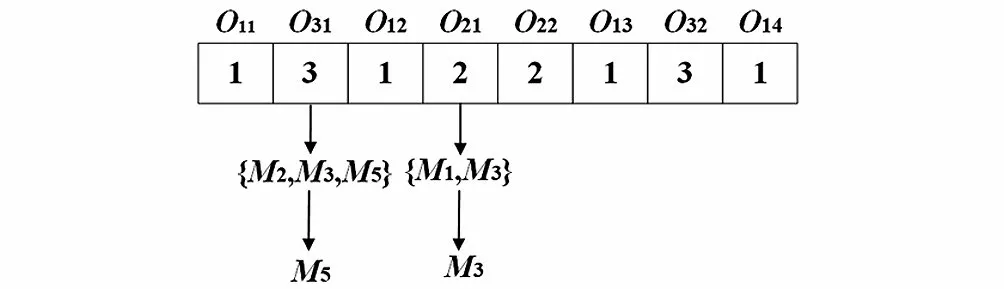
圖1 機器選擇編碼規(guī)則Fig.1 Coding rules of machine selection

(2)工序排序：每個基因由訂單編號編碼。訂單號出現(xiàn)的次數(shù)(工單J有n道工序)表示訂單與工序之間的連續(xù)處理順序，即從左到右編譯染色體，如J1表示訂單1，O11表示訂單1的第1 道工序(圖2)。

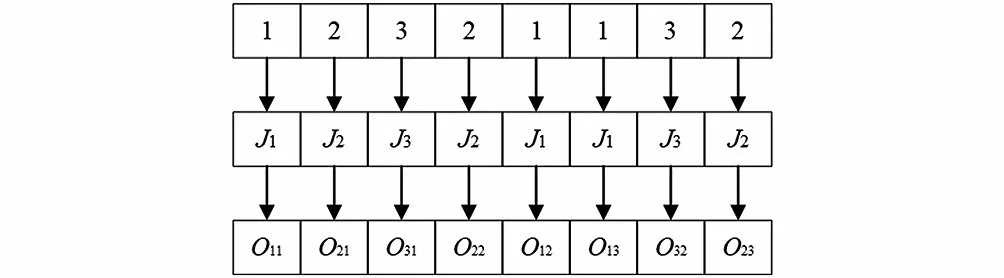
圖2 工序排序編碼規(guī)則Fig.2 Coding rules of process sequencing

依據(jù)機器選擇和工序排序的編碼機制轉換出工序的加工時間，通過每臺機器的生產(chǎn)狀況及對應的加工時間計算出對應機器負荷和最大完工時間。

3.2 混合策略的種群初始化

為了保證初始種群分布均勻且保存種群的多樣性，使用Logistic混沌與均勻分布相結合的混合策略對種群進行初始化。Logistic序列具有全局遍歷性強的優(yōu)點，其方程如下：

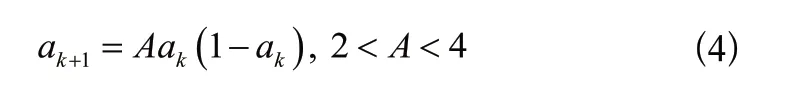
其中，k為迭代的次數(shù)，ak是第k個混沌數(shù)。

針對機器選擇和工序排序進行種群初始化。具體步驟如下。

(1)機器選擇：S為車間可用機器，統(tǒng)計每臺機器當月工作時間，采用均勻分配原則，若某臺機器當月工作時間超過平均工作時間，則優(yōu)先考慮使用其他機器，保證機器的負荷均衡。隨機生成一組數(shù)據(jù)M ij(Mij∈ [0,1])，根據(jù)Logistic方程得到具有混沌序列特性的Mij作為機器選擇的初始方案。

圖3 工序排序Fig.3 Process sequencing

3.3 策層個體位置更新機制

針對多目標問題，灰狼優(yōu)化算法由于多次迭代而難以判斷個體優(yōu)劣。為解決這一問題，采用非支配排序遺傳算法(Non-dominated Sorted Genetic Algorithm-II，NSGAII)的非支配排序及擁擠度方法，將每個個體按照它們的支配與非支配關系進行再分層，提出了擁擠度與擁擠度比較算子，按照擁擠度大小對種群進行排序，并在快速排序后挑選出三組最優(yōu)解集分別為α狼、β狼、δ狼，重復上述，對種群進行更新，從而確定新的三組最優(yōu)解集。

3.4 局部搜索

ω狼是等級最低的階層，需要依賴α狼、β狼、δ狼的信息進行更新，多次運行后會導致種群的多樣性下降，出現(xiàn)早熟收斂現(xiàn)象，因此在算法中融入局部搜索算法對決策層個體進行擾動，設計了以下兩種領域結構。

(1)機器選擇：隨機選取一個訂單，其對應每道工序可選擇的機器為多臺，任意選取一臺不同的機器代替原來的機器。

(2)工序排序：隨機選取兩個不同訂單的工序，將其位置互換。

3.5 精英反向?qū)W習策略

本文使用反向?qū)W習策略提高算法搜索性能和收斂速度。α狼、β狼和δ狼作為狼群中的精英群體，對其進行反向求解，從中發(fā)現(xiàn)潛在的精英個體用于更新父代種群。某一解Di在某個n維空間內(nèi)，D'為反向解，數(shù)學模型如下：

其中，Di∈(ai,bi)，ai= min(Di)，bi= max(Di)，ai和bi為動態(tài)邊界，反向?qū)W習策略解決了固定邊界難以保存搜索經(jīng)驗的問題，使精英反向解能夠在有限的空間中進行搜索且不易陷于局部最優(yōu)。

3.6 算法流程

改進灰狼算法(IGWO)算法求解流程如圖4所示。

圖4 算法流程圖Fig.4 Algorithm flow chart

步驟1：采用混合策略方法將種群初始化，設置當前迭代次數(shù)k=0和最大迭代次數(shù)為kmax。

步驟2：尋找最優(yōu)解，采用NSGAII方法進行非支配排序和擁擠度的計算，選取三個最優(yōu)解集分別為α狼、β狼、δ狼。

步驟3：對α狼、β狼、δ狼進行局部搜索，根據(jù)適應度值大小及狼群公式更新個體位置信息。

步驟4：采用精英反向?qū)W習策略，選取前N個最優(yōu)灰狼個體作為下一代種群。

步驟5：判斷是否滿足終止條件，若滿足，則輸出所有非支配解，若不滿足，則執(zhí)行步驟2。

4 實例驗證與分析(Case verification and analysis)

4.1 案例背景

本文選擇某軟包制造企業(yè)的印刷包裝車間對IGWO進行應用驗證。車間設備信息詳見表2，車間訂單信息詳見表3。

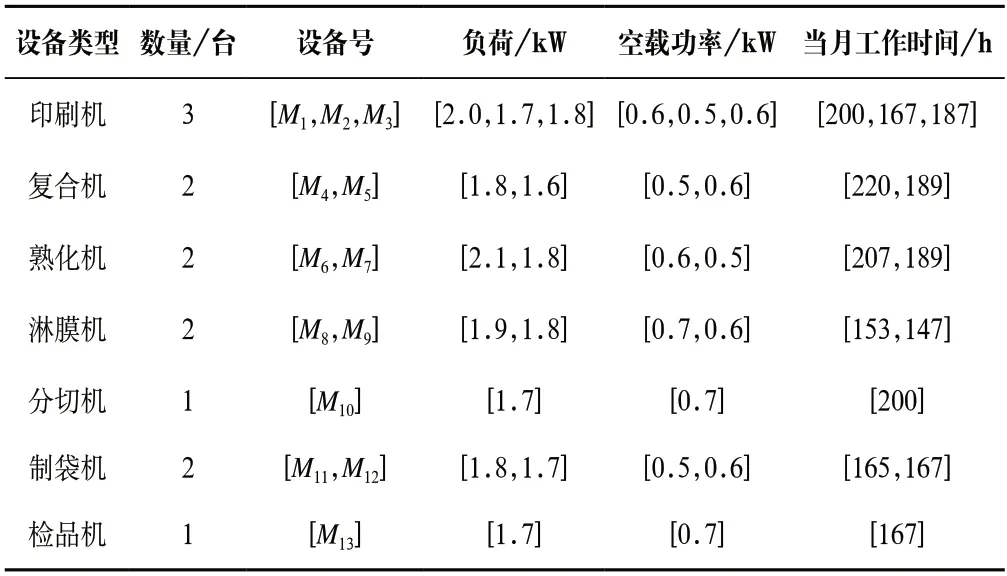
表2 車間設備信息(節(jié)選)Tab.2 Workshop equipment information (excerpt)

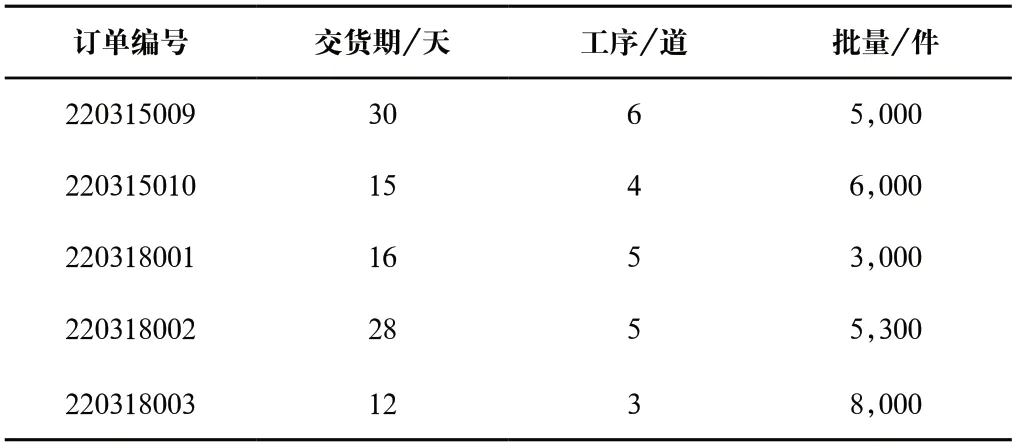
表3 車間訂單信息(節(jié)選)Tab.3 Workshop order information (excerpt)

4.2 案例驗證

根據(jù)企業(yè)的實際需求，三個目標函數(shù)所占權重比為最大完工時間f1＞機器負荷f2＞機器總能耗f3。本文采用AHP(層次分析法)確定最大完工時間、機器負荷、機器總能耗的權重為w= (0.563,0.297,0.14)T。初始種群規(guī)模為200，最大迭代次數(shù)取100。

4.2.1 初始調(diào)度方案

根據(jù)生產(chǎn)車間設備信息和訂單信息，基于改進灰狼算法的動態(tài)調(diào)度技術求解得到初始調(diào)度方案的甘特圖(圖5)。

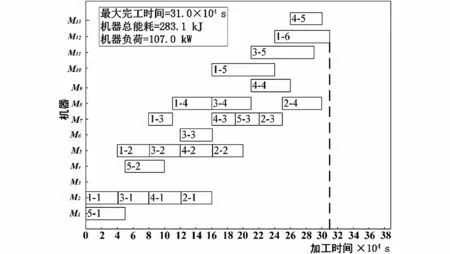
圖5 初始調(diào)度方案甘特圖Fig.5 Gantt chart of initial scheduling scheme

4.2.2 機器故障下的調(diào)度方案

在10，000 s時，機器M5發(fā)生故障，維修時間為18，720 s。機器發(fā)生故障時，各訂單的加工狀態(tài)詳見表4。

表4 機器故障發(fā)生時的各訂單加工狀態(tài)Tab.4 Processing status of each order when machine failure occurs

采用兩種調(diào)度方案：(1)方案1為右移調(diào)度，在初始調(diào)度方案的基礎上，不改變其他工序的調(diào)度順序，將故障機器M8上等待加工的工序往右移18，720 s，如圖6(a)所示；(2)方案2為基于改進灰狼算法的動態(tài)調(diào)度技術求解得到動態(tài)調(diào)度方案的甘特圖，如圖6(b)所示。

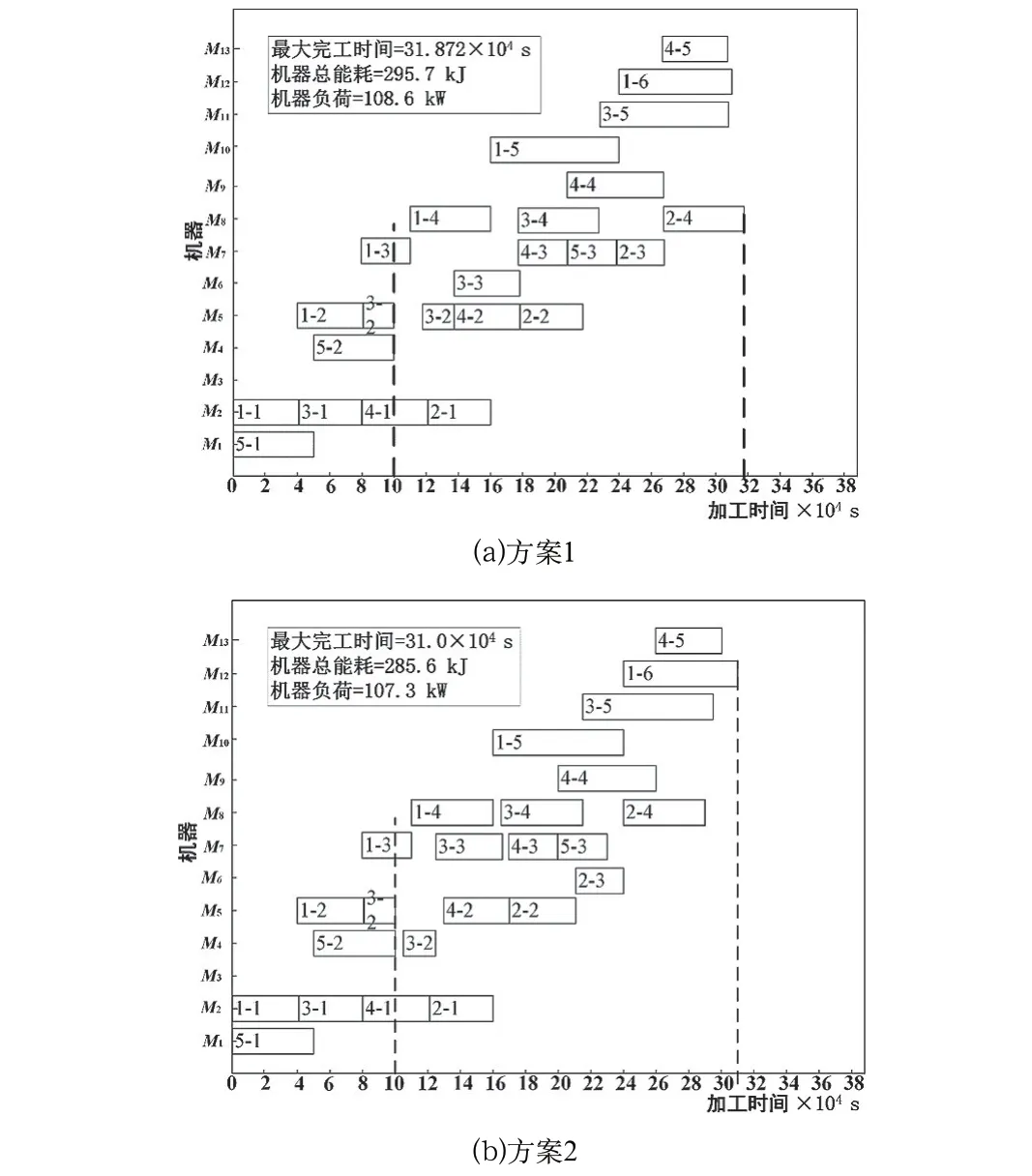
圖6 機器故障重調(diào)度方案Fig.6 Machine fault rescheduling scheme

對比兩種調(diào)度方案，方案2 的最大完工時間減少了2.74%，機器總能耗減少了3.42%，機器負荷減少了1.20%。方案1中的訂單工序不變，機器M5發(fā)生故障后與其相關聯(lián)的工序往后移，導致機器M6、M7、M8、M9、M10、M11、M12、M13的空閑等待時間和機器總能耗都增加。

4.2.3 緊急訂單下的調(diào)度方案

在初始調(diào)度方案執(zhí)行到80，000 s時，車間收到加工件數(shù)量為5，000 件的緊急訂單，需在3 天內(nèi)完成入庫，收到緊急訂單時各工件加工狀態(tài)詳見表5。

表5 收到緊急訂單時的各訂單加工狀態(tài)Tab.5 The processing status of each order when an urgent order is received

分別采用兩種調(diào)度方案：(1)方案1為不改變其他工序的調(diào)度順序，對空閑機器進行工序分配，如圖7(a)所示；(2)方案2為基于改進灰狼算法的動態(tài)調(diào)度技術求解得到動態(tài)調(diào)度方案的甘特圖，如圖7(b)所示。

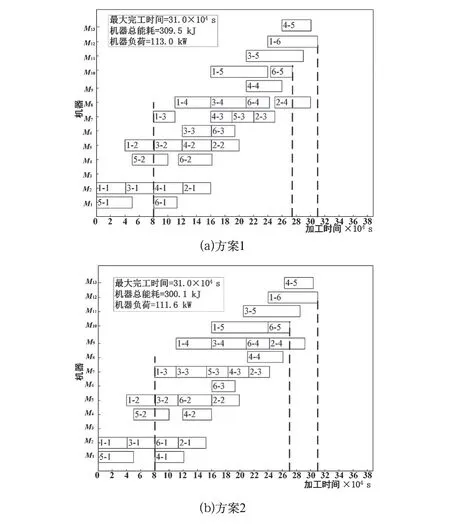
圖7 緊急訂單重調(diào)度方案Fig.7 Emergency order rescheduling scheme

對比兩種調(diào)度方案，雖然最大完工時間相等，但方案2中緊急訂單的完工時間為19.1×104s，方案1中緊急訂單的完工時間為19.5×104s，方案2比方案1提前2.05%完成訂單。方案2的機器總能耗減少了3.04%，機器負荷減少了1.24%，原因是采用改進的灰狼算法對車間未開工的工序進行重調(diào)度，選擇負荷和空載小的機器進行加工，并且縮短了機器的空閑時間；方案1沒有考慮其他工序的影響，只是在初始調(diào)度的基礎上進行調(diào)度。

4.3 與其他算法仿真對比

為了驗證改進灰狼算法的有效性，與NSGAII算法進行比較，分別取機器數(shù)量為20、30、40 臺生成a、b、c三組訂單數(shù)量不同的案例，對每個案例獨立運行20 次，并計算和統(tǒng)計相關評價指標的最小值(min)、最大值(max)和平均值(avg)，測試算法性能的參數(shù)反世代距離(IIGD)、非支配解個數(shù)(NNDS)、非支配解比例(RNDS)，不同實例情況下，IGWO和NSGAII在IIGD、NNDS、RNDS三個方面的對比結果分別如表6、表7、表8所示。

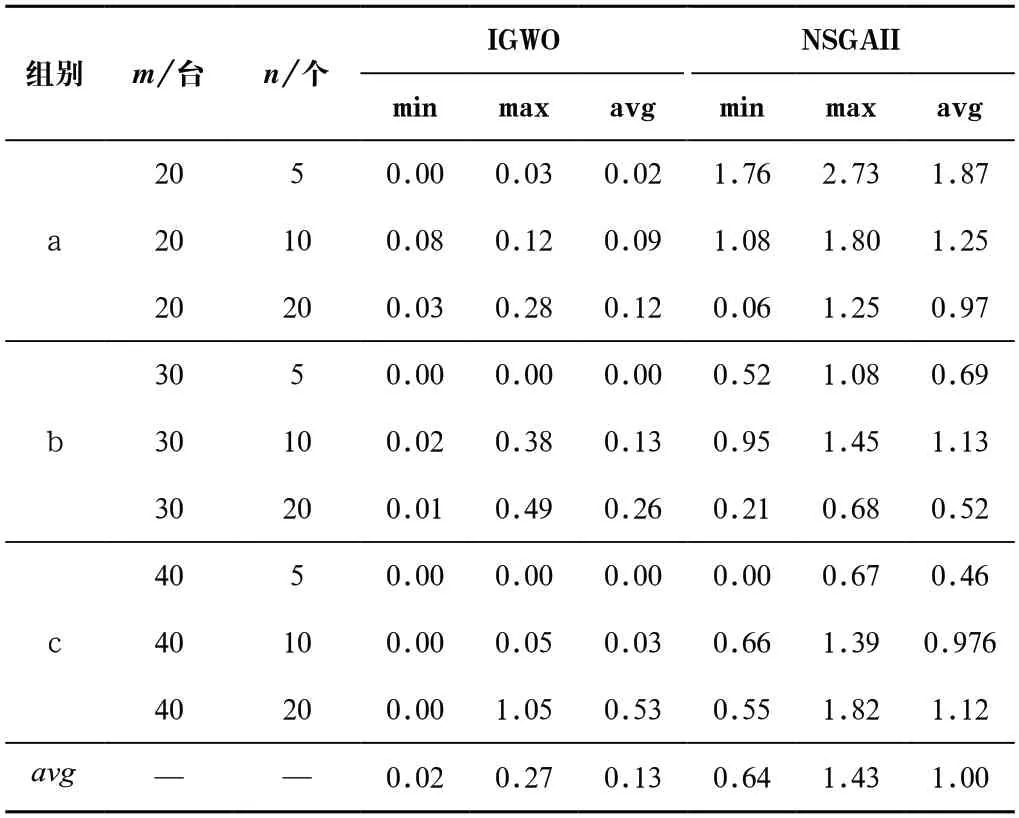
表6 I IGD結果比較Tab.6 Comparison of I IGD results

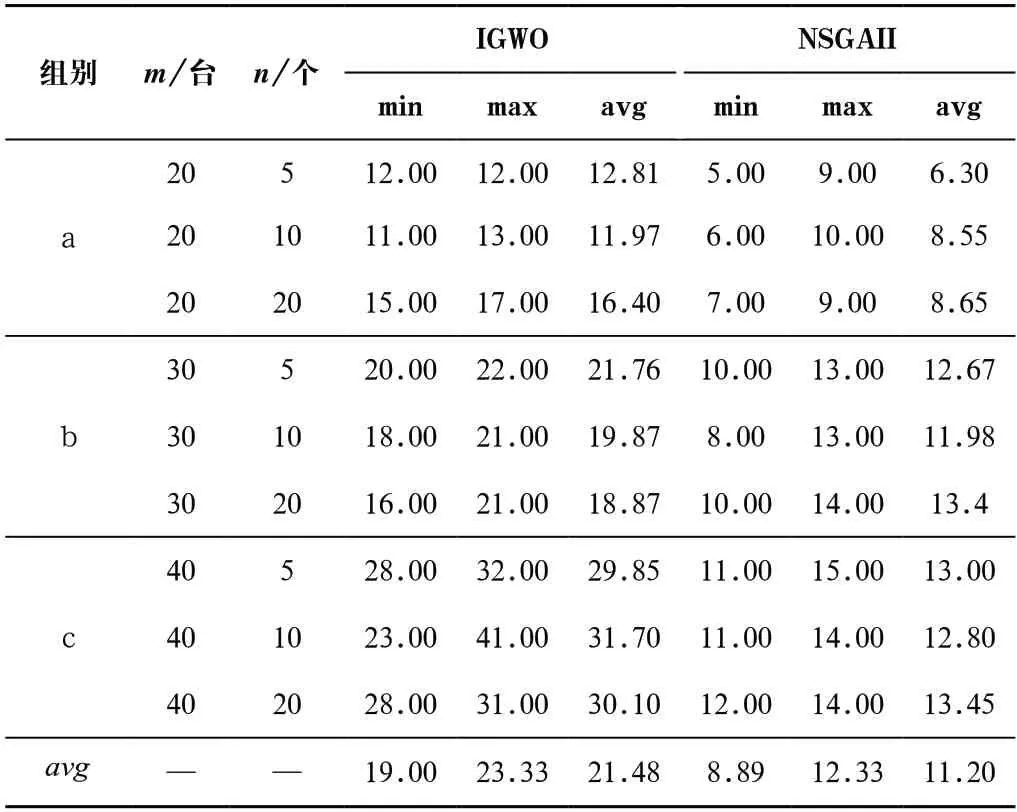
表7 N NDS結果比較Tab.7 Comparison of N NDS results

表8 RN DS結果比較Tab.8 Comparison of R NDS results

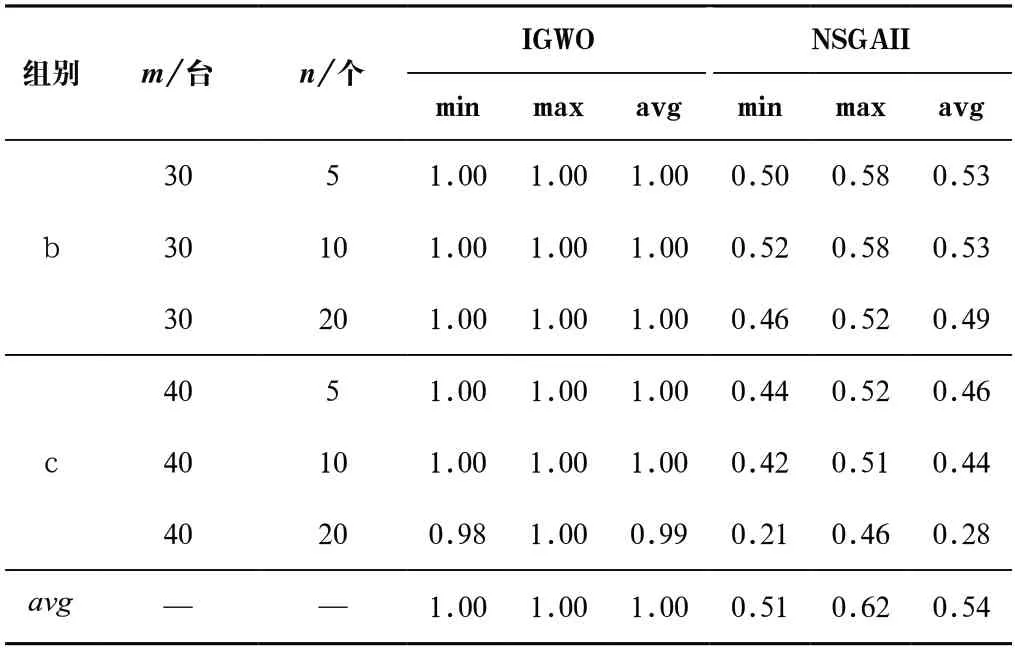
(續(xù)表)

由表6可知，IGWO算法得到IIGD指標的min、max和avg的平均值分別為0.02、0.27、0.13，遠小于NSGAII算法得到的結果0.64、1.43、1.00。由此可得，IGWO算法的收斂性和分布性優(yōu)于NSGAII算法。

由表7可知，IGWO算法得到NNDS指標的min、max和avg的平均值分別為19.00、23.33、21.48，高于NSGAII算法得到的結果8.89、12.33、11.20，從上述實例結果可知，IGWO算法求得NNDS數(shù)量都多于NSGAII算法。

由表8可知，IGWO算法得到RNDS指標的min、max和avg的平均值分別為1.00、1.00、1.00，優(yōu)于NSGAII算法得到的結果0.51、0.62、0.54。

最大完工時間、機器負荷、機器總能耗的權重為w= (0.563,0.297,0.14)T，得出三種調(diào)度事件中的最優(yōu)解(表9)，由表9可知，NSGAII在機器總能耗控制上具有優(yōu)勢，但考慮到IGWO能節(jié)省最大完工時間，因此仍具有較大優(yōu)勢。

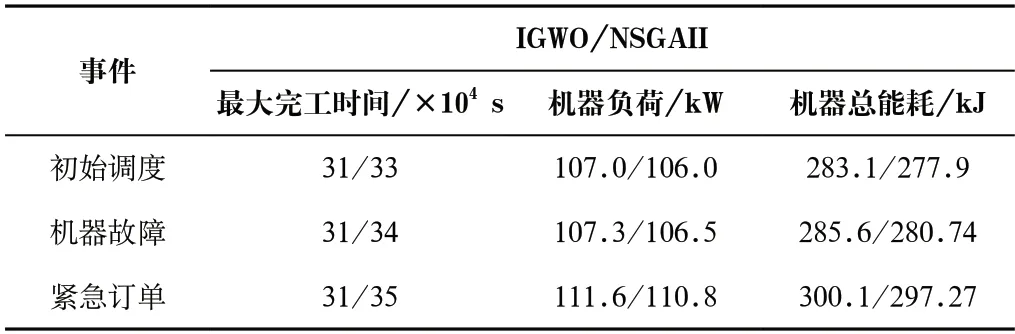
表9 實驗結果Tab.9 Experimental results

5 結論(Conclusion)

本文針對機器故障和緊急訂單兩種動態(tài)事件對印刷包裝車間動態(tài)調(diào)度產(chǎn)生干擾的問題，建立了以最大完工時間、機器負荷和機器總能耗為目標的印刷包裝車間動態(tài)調(diào)度多目標優(yōu)化模型，在此基礎上提出了解決該問題的一種改進灰狼算法。首先，采用Logistic混沌與均勻分布相結合的混合策略初始化種群，從而提高初始化種群的多樣性。為了確定最優(yōu)解集，利用非支配排序遺傳算法的非支配排序及擁擠度方法，按照擁擠度大小對種群進行排序。為了避免算法出現(xiàn)早熟收斂現(xiàn)象，采用兩種鄰域結構對獵物進行鄰域搜索，并且利用精英反向?qū)W習策略優(yōu)化算法搜索性能及收斂速度。其次，通過案例驗證和對比不同方案，證明動態(tài)事件發(fā)生時，所提方法能夠有效降低最大完工時間、機器負荷和機器總能耗。