低溫氮氣中液滴噴霧凍結過程的研究

彭潤玲，翟浩楠，楊 杰，王 威，劉錦悅，曹 蔚，郭俊德

（西安工業(yè)大學 機電工程學院，西安 710000）

0 引言

噴霧冷凍干燥技術是將物料經(jīng)霧化器霧化后與冷介質接觸快速凍結成冰粒，然后在低壓環(huán)境中將冰粒脫水干燥的技術[1]。該技術兼有冷凍干燥與噴霧干燥的優(yōu)點，廣泛應用于納米材料、粉狀食品和藥品的制備[2-4]。

噴霧冷凍干燥法制備的納米粉，粒徑大小不同，從幾納米到幾百納米不等。造成粒徑不同的原因：一方面與樣品本來形態(tài)和前驅體的制備方法有關；另一方面是與噴霧冷凍干燥過程中凍結速率、最終凍結溫度等工藝參數(shù)有關，近年來引起了研究人員的關注。Sebasti?o等[5]建立了一系列常壓噴霧冷凍干燥過程的數(shù)學模型，模型包括單液滴凍結模型、凍結過程傳熱模型和干燥過程傳熱模型。噴霧凍結過程對噴霧冷凍干燥產(chǎn)品質量有較大的影響，研究表明，低溫凍結過程中液滴凍結速率能夠有效影響凍干后物料的粒徑尺寸，并且能夠提高產(chǎn)品的質量[6-9]。

目前限制噴霧冷凍干燥技術推廣應用的主要因素是凍結過程、凍結速率和凍結溫度不易精確控制[10]。因此，建立噴霧凍結過程的數(shù)學模型，通過CFD和實驗對噴霧凍結過程進行仿真和驗證，分析液滴粒徑、氮氣流量和物料流量等因素對物料最終凍結溫度、凍結速率的影響規(guī)律，為精確控制凍結溫度和凍結速率提供理論基礎。

1 模型的建立

1.1 物理模型

噴霧冷凍設備的凍干室結構存在的相變主要為液態(tài)物料放熱并相變?yōu)楣虘B(tài)物料，氮氣吸熱溫度升高，液體汽化與冰升華雖然存在，但相比之下量很少可以忽略不計。為了便于研究，將凍干室結構簡化，簡化后物理模型如圖1所示，其內(nèi)層腔體直徑為180 mm，高度為380 mm；外腔直徑260 mm，高度為420 mm。

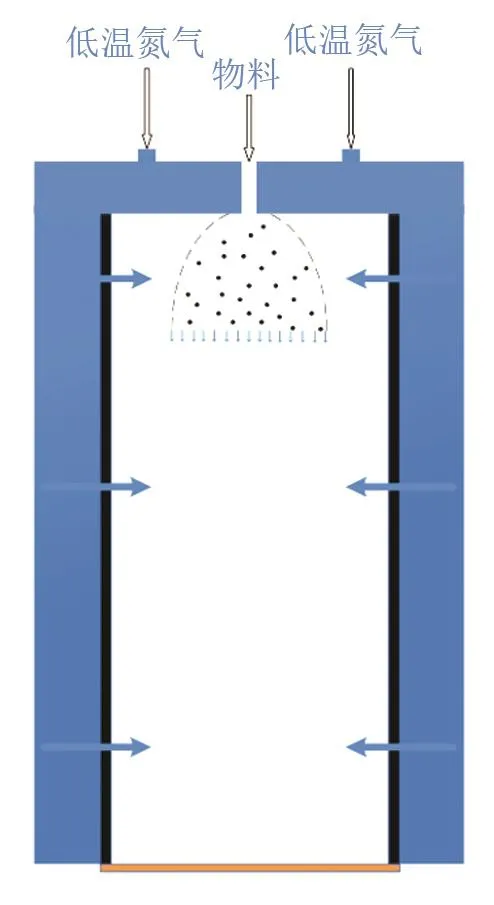
圖1 凍干室結構的簡化物理模型Fig.1 The simplified physical model of the lyophilisation chamber structure

1.2 數(shù)學模型

1.2.1 液滴位移模型

霧化液滴在整個凍結過程做斜拋運動，在簡化模型時定義所有霧化液滴初始速度的豎直分量均為vz，因此整個下落過程液滴各位置的豎直方向加速度a可以根據(jù)牛頓第二定律計算：

式中：g為重力加速度；Ff為阻力（拖拽力）；md為液滴質量；a為液滴在某點的加速度。

霧化液滴在向下運動過程中會受到相應的氣體阻力Ff，氣體阻力可以由式（2）進行計算。

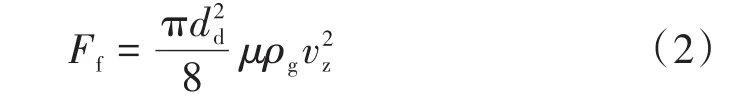
式中：dd為液滴直徑；ρg為氣體密度；vz為液滴在某點的速度。

阻力系數(shù)μ可以根據(jù)式（3）進行求解。

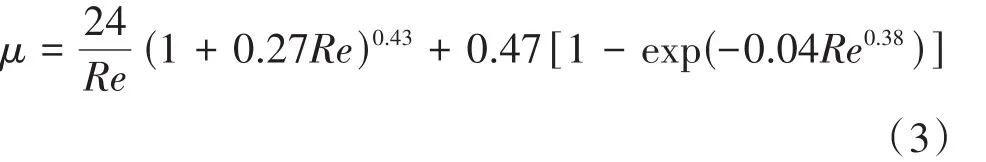
式中：Re為雷諾數(shù)。

霧化液滴在運動一段時間t后，霧化液滴所處的凍干室內(nèi)位置可以由液滴向下運動的豎直位移xz表示，xz可以根據(jù)式（4）和（5）聯(lián)立求解。

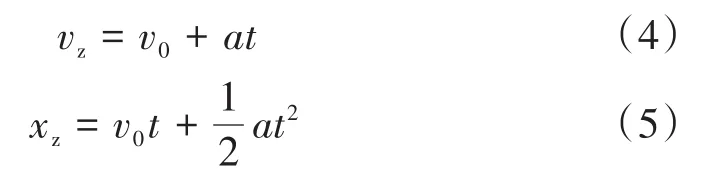
式中：t為液滴運動到某點時的時間；v0為液滴豎直方向初始速度。

1.2.2 噴霧凍結過程單液滴凍結模型

在使用集總熱容法時要考慮實際情況中的畢渥數(shù)Bi的范圍，畢渥數(shù)Bi可以根據(jù)式（6）進行求解：

式中：hd為液態(tài)液滴對流換熱系數(shù)；k為熱導率。

為減小使用集總熱容法時帶來的誤差，要求Bi＜0.1時才使用集總熱容法。設液滴直徑dd=0.000 1 m，水的導熱系數(shù)kwater=0.566 W/（m·K），冰的導熱系數(shù)kice=2.26 W/（m·K），對流傳熱系數(shù)hd=150 W/（m2·K）[11]，霧化物料為液態(tài)或固態(tài)時畢渥數(shù)Bi均小于0.1，因此水的噴霧凍結過程可以使用集總熱容法。

采用集總熱容法建立液滴凍結速率模型，液滴內(nèi)部溫度梯度忽略不計，則液滴溫度降至共晶點溫度TP時，所需時間t1與降溫速率vT1為：

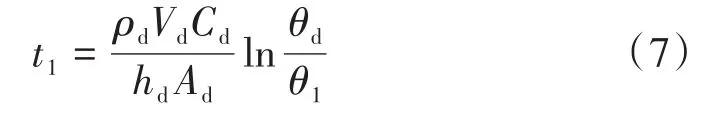
式中：ρd為液態(tài)液滴密度；Vd為液滴體積；Cd為液態(tài)液滴比熱容；Ad為液滴表面積；θd為液滴與氮氣的溫度差；θ1為液滴相變溫度與氮氣溫度之間的差。

式中：Td為液滴溫度；Tp為液滴相變溫度；t1為液滴溫度降至共晶點溫度所需時間。

根據(jù)體積Vd與表面積Ad公式：

式（7）可以改寫為：

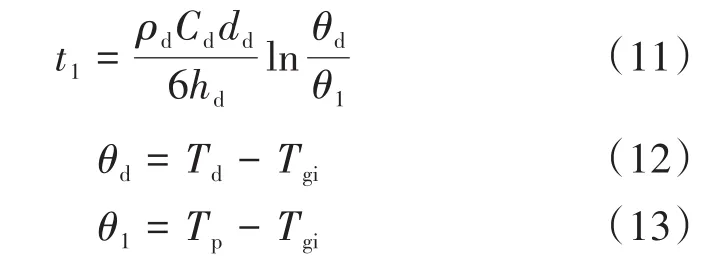
式中：ρd為液態(tài)液滴密度；Tgi為氮氣溫度。

相變階段時，液滴相變時間t2與相變傳熱總能量Q2之間的關系為：

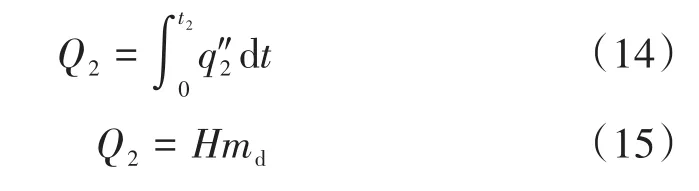
式中：q″2為液滴相變階段的熱流密度；H為液滴凍結潛熱。

冰粒降溫階段，冰粒從共晶點溫度Tp至預設最終凍結溫度Tice所需時間t3：

式中：ρice為冰的密度；hice為冰粒對流傳熱系數(shù)；Cice為冰粒的比熱容；θp為共晶點溫度與氮氣溫度之差；θ2為冰與氮氣之間的溫度差。

式中：Tp為共晶點溫度；Tice為冰的溫度。

1.2.3 噴霧凍結過程能量傳輸模型

建立噴霧凍結過程中霧化液滴與氮氣之間的能量傳輸模型[12-13]，并預測氮氣的實時溫度Tgi。霧化液滴從霧化噴嘴噴出時的初始溫度Td0，直至液滴凍結并降溫至相變溫度以下T，所釋放熱量Qz為：

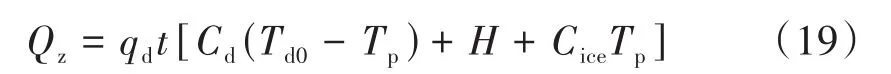
式中：Qz為液滴在整個噴霧凍結階段釋放總熱量；qd為液滴流量；Td0為液滴初始溫度。

在整個過程中氮氣吸收的熱量包括霧化液滴釋放的熱量、凍干室壁面降溫所釋放的熱量以及外界輻射傳熱所傳輸?shù)臒崃俊Ｔ诖诉^程中氮氣吸收的熱量Qx與霧化液滴釋放的熱量Qz相等，即Qx=Qz。氮氣另外吸收的熱量定義為氮氣系統(tǒng)的熱損失，設熱損失系數(shù)為λ。氮氣在凍干室的出口溫度與氮氣熱量變化之間的關系為：

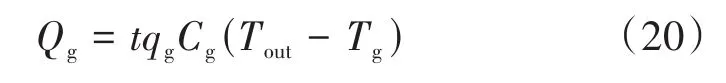
式中：Qg為氮氣在整個噴霧凍結階段釋放總熱量；qg為氮氣流量；Cg為氮氣的比熱容；Tout為出口氮氣溫度；Tg為入口氮氣溫度。

氮氣吸收的熱量Qx為：

2 數(shù)值模擬結果與分析

本文利用Fluent模擬了噴霧凍結過程，采用SIMPLE算法求解器求解[14-16]。模擬仿真前對建立的凍干室模型進行網(wǎng)格劃分，如圖2所示，并將模擬過程的邊界條件設置如表1所列。

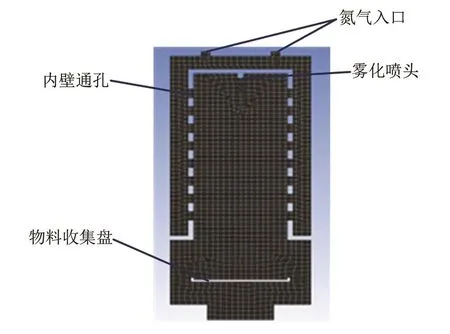
圖2 凍干室模型網(wǎng)格劃分Fig.2 Freeze-drying chamber model meshing

表1 仿真過程中的邊界條件設置Tab.1 Boundary condition settings during the simulation

2.1 氮氣流量與最終凍結溫度和凍結速率間的響應規(guī)律

根據(jù)模擬仿真，當液滴流量為5 g/s，氮氣初始溫度為150 K，氮氣流量分別為40 g/s、50 g/s和60 g/s時，霧化液滴溫度圖像如圖3所示。在凍干室內(nèi)設置三個不同位置的監(jiān)測點，對3個監(jiān)測點液滴溫度進行測量分析（如圖4所示），得出凍干室內(nèi)不同位置液滴溫度與氮氣流量之間的關系圖，如圖5所示。

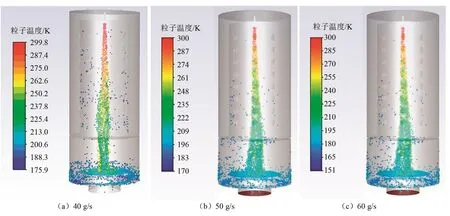
圖3 不同氮氣流量霧化液滴溫度分布圖Fig.3 Temperature distribution of atomized droplets with different nitrogen flow rates

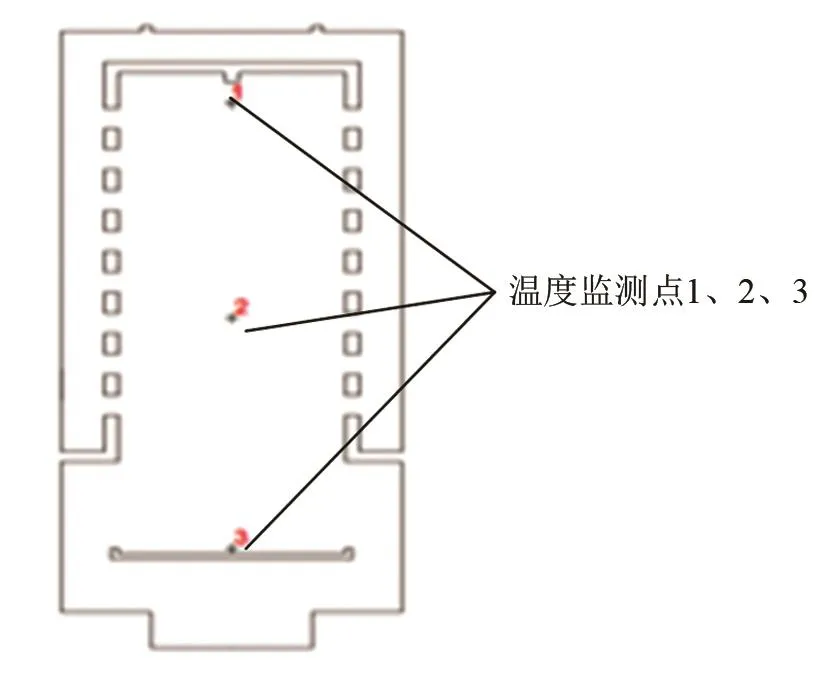
圖4 監(jiān)測點位置Fig.4 Location of monitoring points

圖5 監(jiān)測點液滴溫度變化圖Fig.5 The droplet temperature change diagram at the monitoring point

如圖6所示，將噴霧凍結過程最終凍結溫度數(shù)學模型求解結果與模擬結果對比，可知數(shù)學模型求解結果與模擬結果趨勢相同，最終凍結溫度最大相差10 K，最大誤差率為4%。

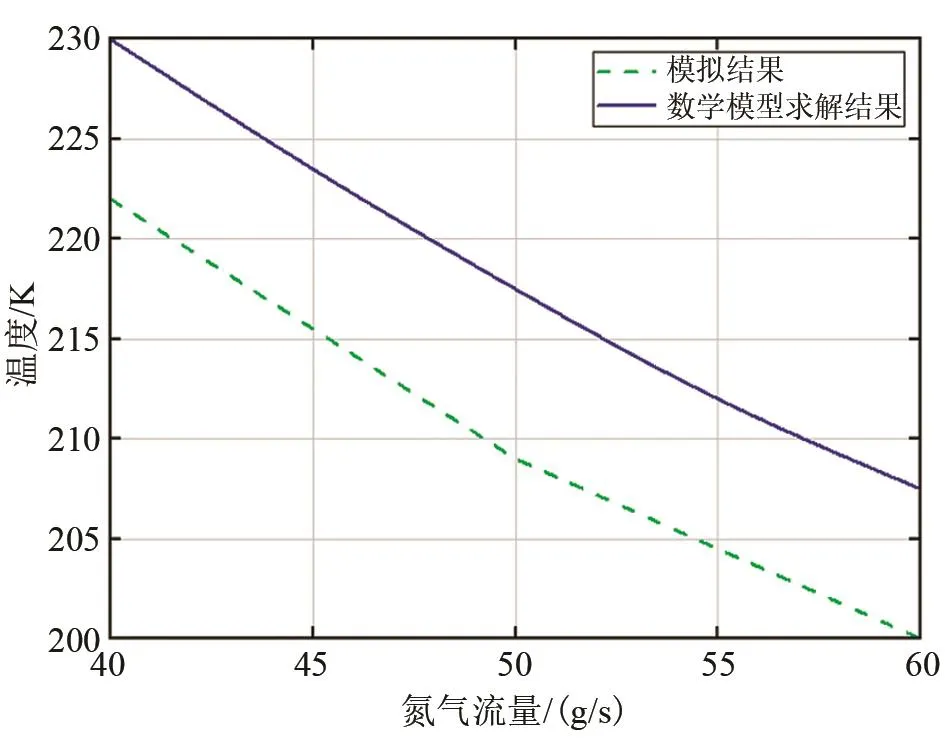
圖6 氮氣流量與液滴最終凍結溫度的關系Fig.6 Relationship between nitrogen flow rate and final freezing temperature of droplets

液滴自霧化器噴出降落至物料收集盤所需時間約為0.13 s，結合圖5中監(jiān)測點1與監(jiān)測點3溫度差可計算出模擬過程氮氣流量液滴平均凍結速率。對比液滴在凍結過程中平均凍結速率的數(shù)學模型求解結果與模擬結果，如圖7所示，當?shù)獨饬髁吭?0 g/s左右時誤差較大，最大相差20 K/s，最大誤差率為3.3%。

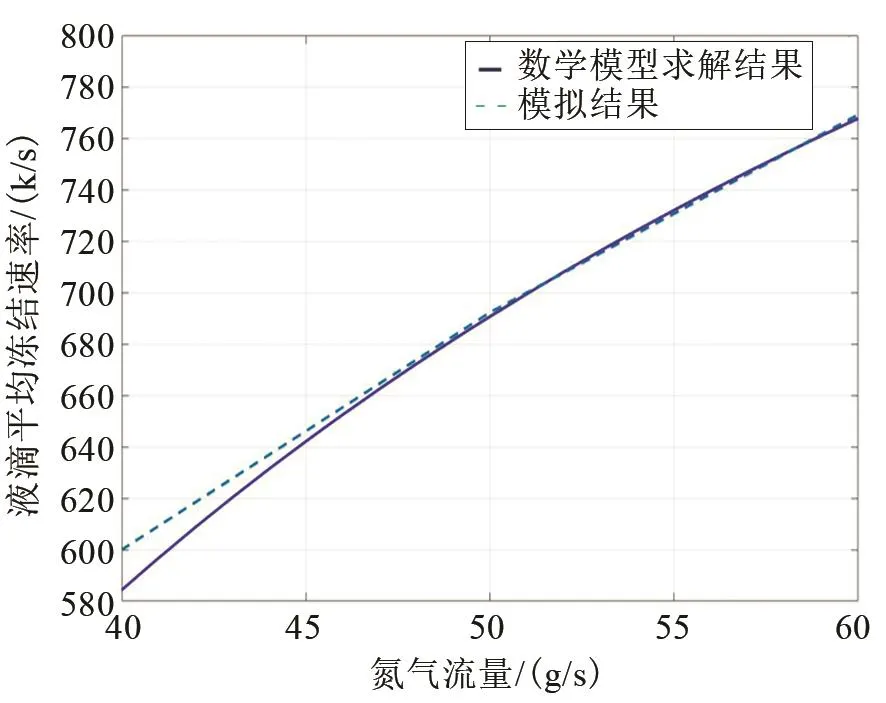
圖7 氮氣流量與液滴平均凍結速率的關系Fig.7 Relationship between nitrogen flow rate and average droplet freezing rate

2.2 物料流量與最終凍結溫度和凍結速率間的響應規(guī)律

當?shù)獨饬髁繛?0 g/s，液滴流量分別為3 g/s、5 g/s和8 g/s時，仿真過程穩(wěn)定后霧化液滴溫度圖像如圖8所示。對監(jiān)測點液滴溫度進行分析，得出凍干室內(nèi)不同位置液滴溫度與氮氣流量之間的關系，如圖9所示。

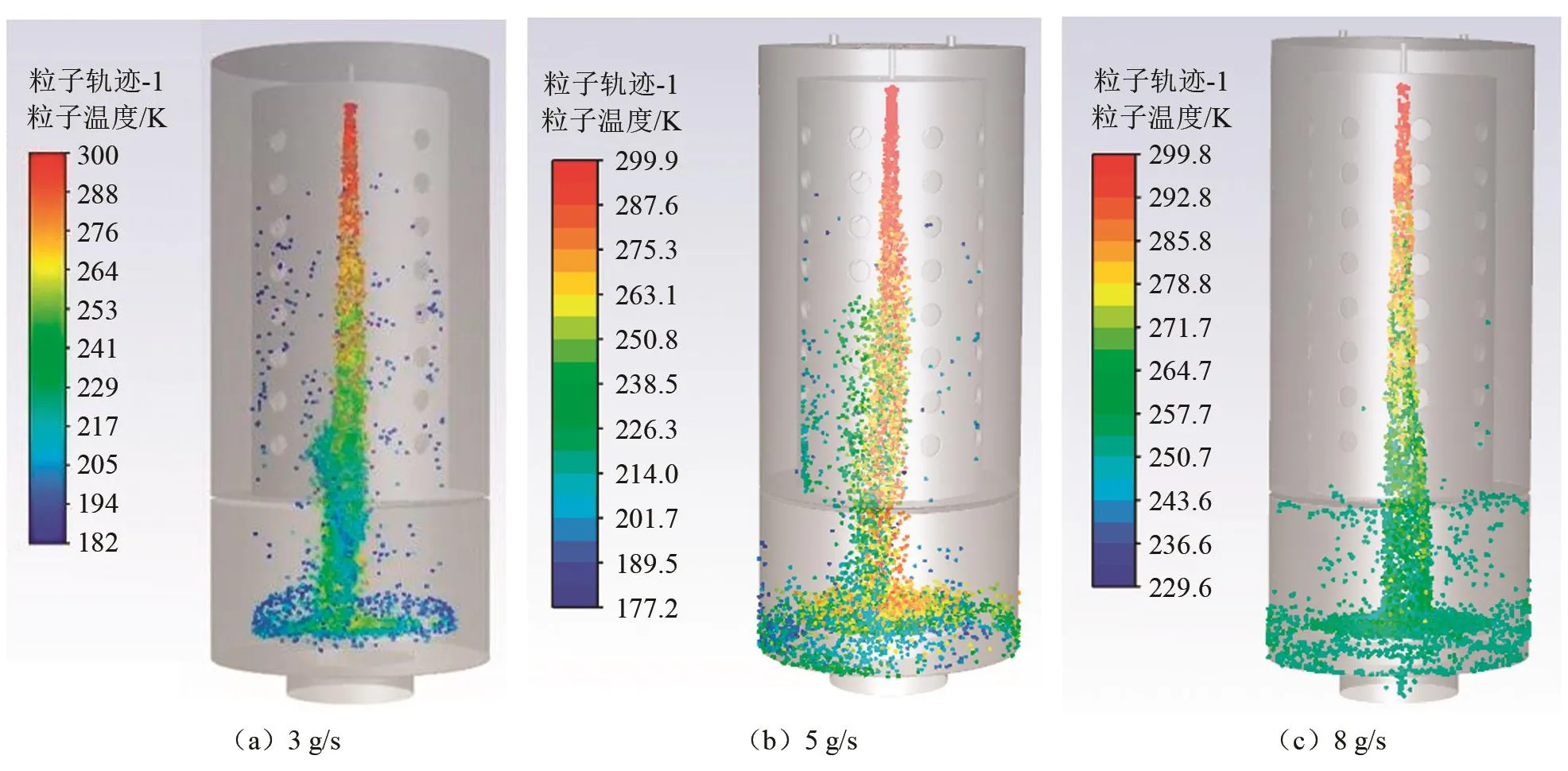
圖8 不同液滴流量霧化液滴溫度分布圖Fig.8 Temperature distribution of atomized droplets with different droplet flow rates

將噴霧凍結過程最終凍結溫度數(shù)學模型求解結果與模擬結果對比，如圖10所示，數(shù)學模型求解結果與模擬結果趨勢相同，最終凍結溫度相差在10 K以內(nèi)，最大誤差率為3.7%。結合圖9中監(jiān)測點1與監(jiān)測點3溫度差可計算出模擬過程中液滴的平均凍結速率。

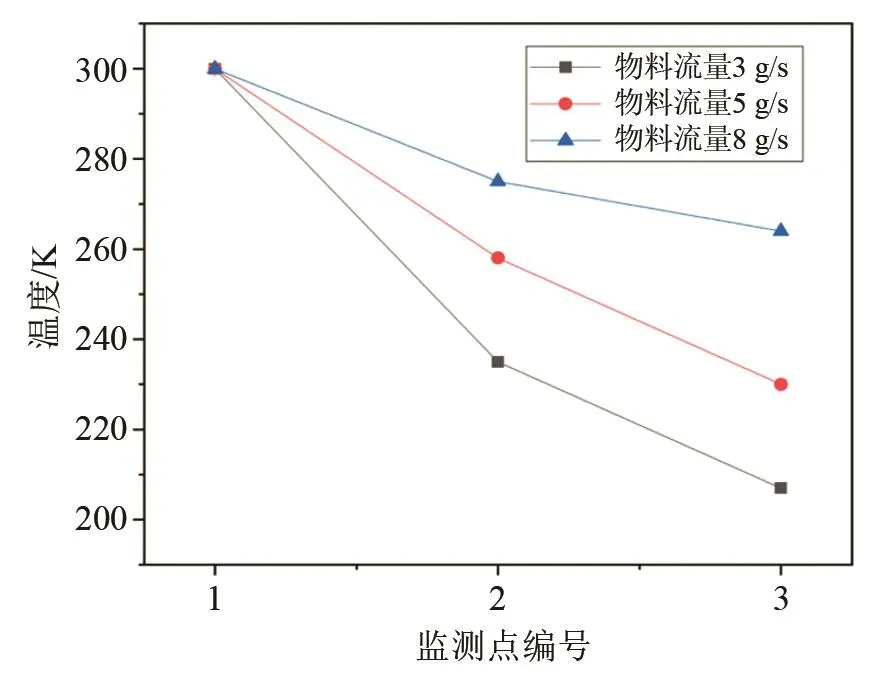
圖9 監(jiān)測點液滴溫度變化圖Fig.9 The droplet temperature change diagram at the monitoring point

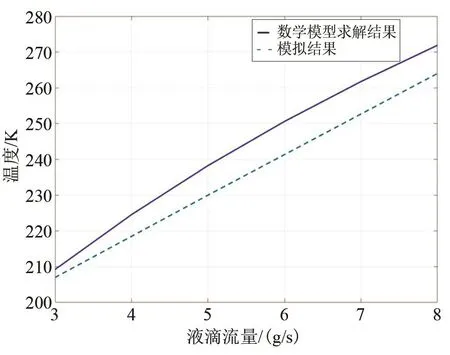
圖10 液滴流量與液滴最終凍結溫度的關系Fig.10 The relationship between droplet flow and final freezing temperature of droplets

如圖11所示，當?shù)獨饬髁坎蛔儯旱瘟髁恐饾u增大到4 g/s時誤差逐步減小，當液滴流量從4 g/s增大時誤差逐步增大，最大誤差率為7.1%。

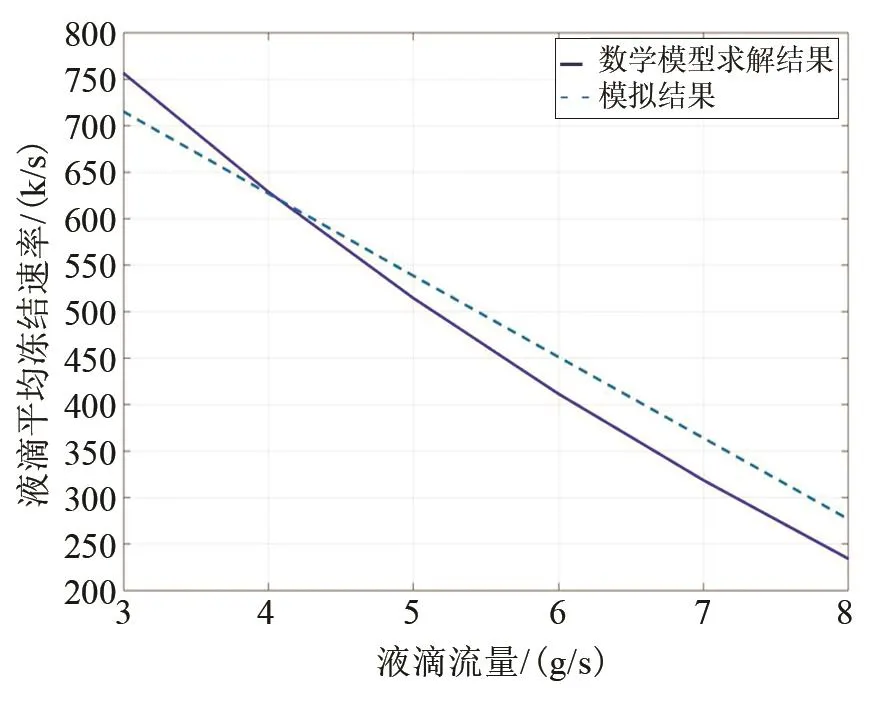
圖11 液滴流量與液滴平均凍結速率的關系Fig.11 The relationship between droplets flow and the average freezing rate of droplets

3 實驗結果與數(shù)學模型求解結果的對比分析

在改進后的實驗型噴霧冷凍干燥機上進行噴霧凍結實驗。實驗初始條件為：氮氣初始溫度為103 K，液滴粒徑為30 μm，物料流量為3 g/s，通過調節(jié)氮氣出口閥壓力來控制氮氣流量，壓力維持在0.3 MPa，然后進行噴霧凍結實驗[17-18]。以相同的條件在實驗型噴霧冷凍干燥機上重復3次實驗，實驗結果如圖12所示，實驗結果平均值如圖13所示。

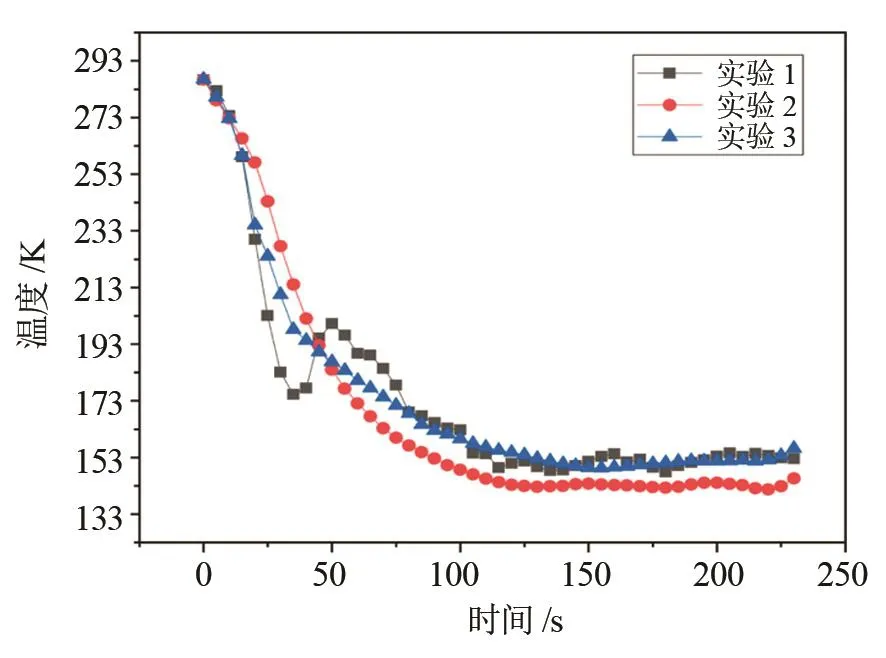
圖12 噴霧凍結實驗最終凍結溫度Fig.12 The final freezing temperature of the spray freezing experiment

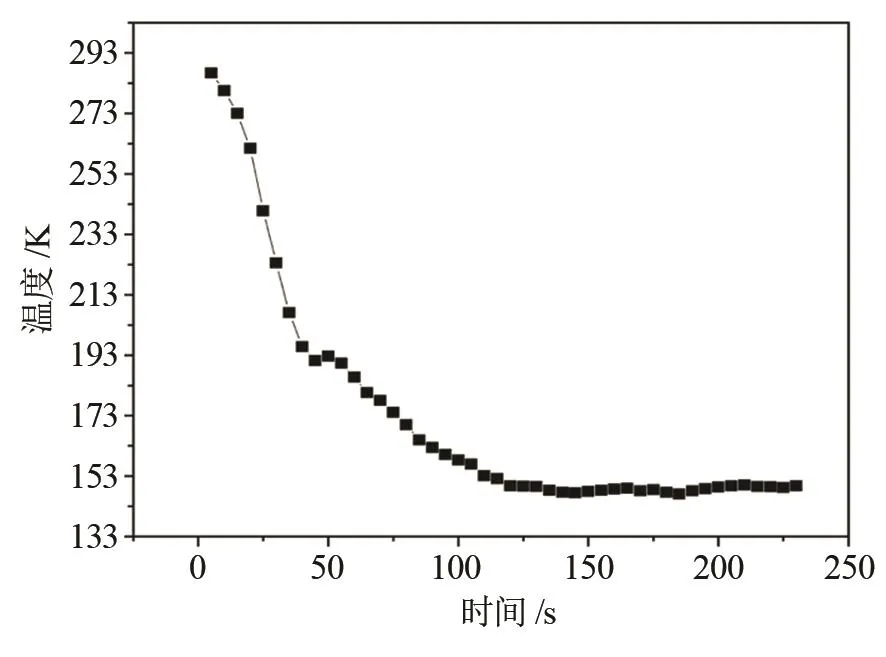
圖13 噴霧凍結實驗平均最終凍結溫度Fig.13 The average final freezing temperature of the spray freezing experiment

氮氣入口壓力選擇及對應氮氣流量如表2所列。不同氮氣流量下監(jiān)測點2、3霧化液滴最終凍結溫度如表3所列。

表2 不同氮氣入口壓力下相應氮氣流量Tab.2 Corresponding nitrogen flow rate under different nitrogen inlet pressures

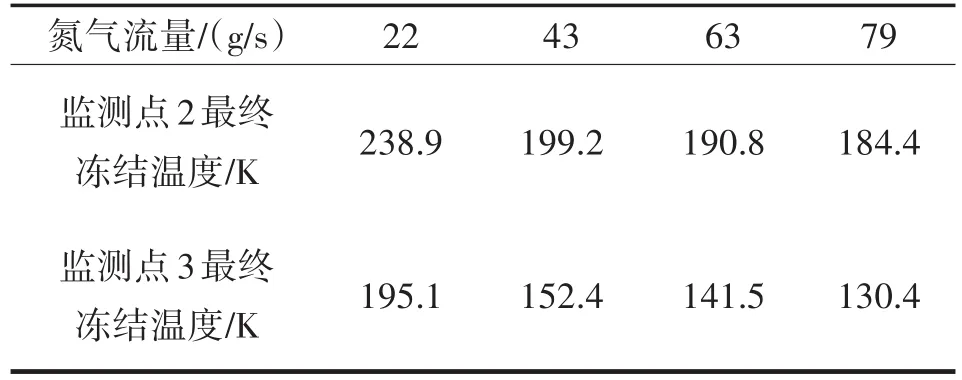
表3 不同氮氣流量下監(jiān)測點2、3最終凍結溫度Tab.3 Final freezing temperature of monitoring points 2 and 3 under different nitrogen flow rates

將表3的實驗結果與數(shù)學模型求解結果對比，如圖14所示。

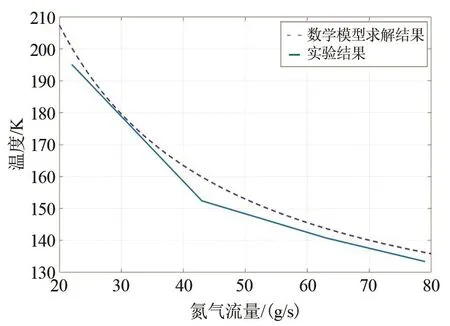
圖14 最終凍結溫度與氮氣流量關系Fig.14 The relationship between final freezing temperature and nitrogen flow

由圖14可知，氮氣流量對最終凍結溫度影響趨勢的實驗結果與數(shù)學模型求解結果基本一致，數(shù)值結果較為接近，最大相差不超過8 K，數(shù)學模型求解結果相對實驗結果最大誤差率為5.2%。

4 結論

采用集總熱容法建立了噴霧凍結過程的數(shù)學模型，求解得到氮氣流量和液滴流量對液滴最終凍結溫度和凍結速率的影響規(guī)律。為驗證所建立數(shù)學模型的準確性，以水為對象利用Fluent軟件對噴霧凍結過程進行了模擬仿真，將模擬仿真結果與數(shù)學模型求解結果對比發(fā)現(xiàn)：平均凍結速率最大相差不超過20 K/s，最大誤差率為7.1%；最終凍結溫度兩者相差在10 K以內(nèi)，最大誤差率為4%，可能是仿真所設置的邊界條件不夠精確導致出現(xiàn)了誤差。但從整體上看，數(shù)學模型求解結果與模擬仿真結果吻合度較好，驗證了數(shù)學模型的準確性。

利用改進后的實驗型噴霧冷凍干燥機進行驗證實驗。對比實驗結果發(fā)現(xiàn)，噴霧凍結實驗結果與數(shù)學模型求解結果最大相差8 K，相對實驗結果誤差率最大為5.2%。該數(shù)學模型可以為建立噴霧凍結自動控制系統(tǒng)提供一定的借鑒。