巧用畫圖策略 助力難點突破
楊燕華



難點一:以圖辨析,明確概念本質
平行線的定義中含有三要素:①在同一平面內;②不相交;③兩條直線。對平行線的概念,我們可以分三個方面進行解讀:第一層次,不能忽略或丟掉“同一平面內”這個前提條件,否則不一定是平行線;第二層次,平行線是指兩條直線,而不是兩條射線或線段;第三層次,線段和射線平行都是指線段或射線所在的直線平行。
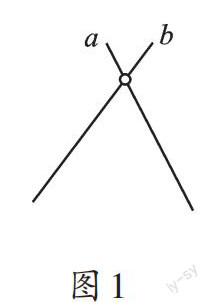
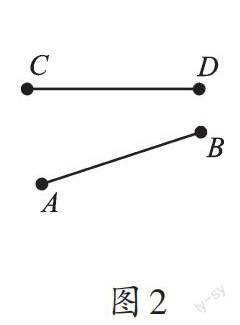
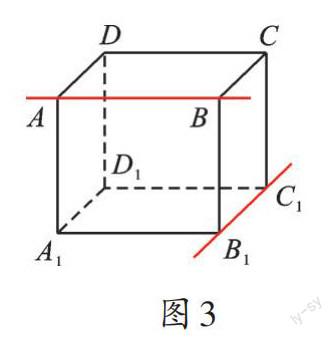
案例1 圖1—圖3中的兩條直線平行嗎?
【解析】圖1—圖3中的兩條直線都不平行。平行線的概念比較抽象,有些同學不理解概念,不妨借助圖形明確概念本質。
難點二:以圖助析,理清性質要點
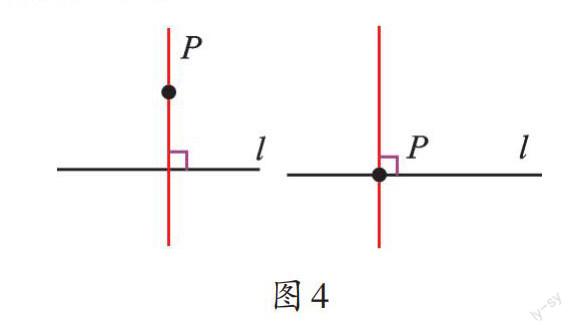
學習垂線的性質,要與平行線的性質前后關聯。垂線的性質1說明了垂線的唯一性,即過一點“有”且“只有”一條直線與已知直線垂直,并且這一點具有任意性。注意,“任意一點”有兩種可能:一是點在直線外,二是點在直線上(如圖4)。這與平行線的性質中“必須過直線外一點”有區別,同學們在解有關問題時要特別注意。
垂線的性質2指出垂線段最短。從直線外一點向直線作垂線,這一點與垂足之間的線段叫作垂線段,這一點與直線上其他各點之間的線段都可以叫斜線段。根據性質1,垂線段是唯一的,而斜線段可以有無數條,并且垂線段的長度總是小于斜線段的長度。
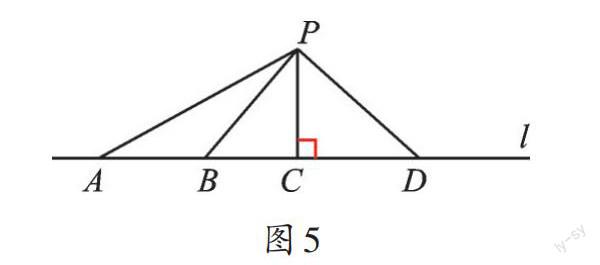
如圖5,直線l外一點P與直線l上的點連接所成的線段中,因為PC⊥l,所以線段PC比PA、PB、PD都短。
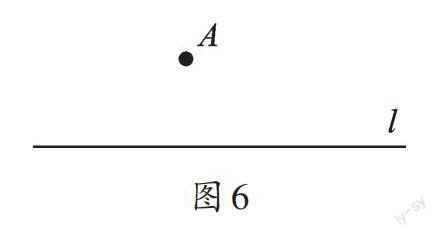
案例2 鐵路l旁有一座村莊A,現要建一個火車站,為了使村莊人乘火車方便,請你選址建火車站,并說明理由。
【解析】乘車最方便,也就是要求距離最近,而根據垂線段最短,則過點A作垂線段即可。
難點三:以圖為媒,指明畫圖方法
1.平行線的畫法
在小學,同學們就學過畫平行線的方法:①平移三角板畫平行線;②利用網格線畫平行線。在網格紙上,所有橫線互相平行,所有豎線也互相平行,我們也可沿著網格的對角線斜著畫,如:斜線段AB是a×b長方形的對角線,所以平移后的線段也是a×b長方形的對角線。畫平行線的依據就是圖形的平移。
2.垂線的畫法
根據垂直的定義可知,畫垂線也就是作直角。因為直角的兩條邊所在的直線是垂直的,所以,垂線的畫法通常有三種:①利用三角板的兩條直角邊或刻度線與所在邊的垂直關系,基本步驟是:一靠、二過、三畫;②利用量角器畫,主要通過畫一個90°的角來得到垂線;③利用網格線來畫,如:以線段AB為對角線的a×b長方形繞著某一點逆時針旋轉90°后得到的b×a長方形的對角線即是符合要求的圖形。
案例3 請利用網格畫線,過點C畫AB的平行線,過點B畫AB的垂線。
【解析】如圖7,畫平行線和垂線的本質就是圖形的運動變換。
難點四:以圖為引,探索操作類題目
同一平面內兩條直線的位置關系,要么是平行,要么是相交。要研究交點的問題,同學們可以借助畫圖的方法,在操作中加以體驗和理解。
案例4 同一平面內的兩條直線,平行沒有交點,如果相交,只有一個公共點。在同一平面內,三條直線公共點的個數可以是____________。四條呢?在同一平面內,n條直線最多有多少個交點呢?
【解析】同一平面內,三條直線的交點個數可以是0、1、2、3,如圖8。
四條直線的交點個數可以是0、1、3、4、5、6。
n條直線的交點個數最多是1+2+3+…+(n-1)=[n(n-1)2]。
變式:1條直線可以把一個平面分成二部分,2條直線可以把一個平面分成三部分或四部分;那么,3條直線可以把平面分成幾部分呢?4條呢?
同學們,畫圖時要注意圖形位置的各種可能性,不能想當然,不能想怎么畫就怎么畫,解題時既要做到心中有數,更要做到心中有圖。
(作者單位:江蘇省無錫市新城中學)

