多交叉曲梁簧片柔性鉸鏈的力學建模與性能分析

陳 鑫 劉江南 龍汪鵬 呂劍文

湖南大學汽車車身先進設計制造國家重點實驗室，長沙，410082

0 引言

柔性鉸鏈無間隙、無摩擦的優點使其在精密工程領域獲得廣泛應用。由兩個彈性簧片在中點處交叉組成的雙交叉簧片柔性鉸鏈具有較大的運動行程和較低的轉動剛度，但轉動精度較低[1]。對此，學者們通過改變簧片交叉點位置[2]、設計變厚度簧片[3]等方式改進其雙簧片結構，但是均難以實現準零軸漂的高轉動精度。

為進一步提高轉動精度，學者們通過增加簧片數量n(n≥3)和采用對稱布局，設計分析了不同多交叉簧片柔性鉸鏈構型。畢樹生團隊率先提出了廣義三交叉簧片柔性鉸鏈[4]，通過加強簧片位移約束提高了轉動精度；后續通過改變交叉點位置，總結了多交叉簧片柔性鉸鏈的多種拓撲構型，并通過仿真進行了綜合性能對比[5]；根據對比結果，重點研究了三交叉簧片形式的內外環柔性鉸鏈的剛度特性[6]；并進一步研究了圓周對稱的多交叉簧片柔性鉸鏈的內部約束特性[7]。DU等[8]基于TRIZ創新原理，提出一種高精度的全對稱多交叉簧片柔性鉸鏈。上述研究中柔性鉸鏈的彈性簧片均為直梁型結構。在多交叉簧片柔性鉸鏈構型中，直梁簧片存在剛度和應力較大、轉角范圍較小等不足[7]。

相比直梁簧片，曲梁簧片具有低剛度、低應力的優點，可實現較大撓度[9]。有學者將樣條曲梁簧片[10-11]、圓弧曲梁-直梁組合的折疊簧片[12]和雙曲梁簧片[13]應用于環形柔性鉸鏈構型[14-15]，以降低轉動剛度和增大轉角范圍。多交叉簧片柔性鉸鏈構型相比環形柔性鉸鏈構型具有更大轉角范圍[6]，但是應用曲梁結構的設計研究鮮有報道，尚缺乏對應的大變形力學分析模型。

本文以圓弧曲梁簧片為變形單元，在分析多交叉簧片柔性鉸鏈對稱拓撲構型的基礎上，提出一種在純轉矩作用下具有零軸漂特性的多交叉曲梁簧片柔性鉸鏈，實現轉動剛度和變形應力的優化。為精確分析其性能，基于梁約束模型(beam constraint model，BCM)[16]建立圓弧曲梁簧片變形模型，并推導圓弧曲梁變形應力方程。應用鏈式梁約束模型(chained beam constraint model，CBCM)[17]進行多交叉曲梁簧片柔性鉸鏈的大變形力學分析建模，通過實驗和有限元仿真驗證理論模型的準確性；進一步分析不同簧片設計變量對柔性鉸鏈轉動剛度和簧片變形應力的影響，探究不同剛度特性的參數設計方案。

1 圓弧曲梁簧片變形建模

圓弧曲梁簧片具有恒定曲率和較大的偏轉范圍[18]，有利于設計多交叉簧片柔性鉸鏈。首先定義圓弧曲梁簧片的相關設計變量，實現其參數化設計。進而根據簧片尺寸建立載荷-位移關系和推導變形應力方程，完成圓弧曲梁簧片的變形建模，為后續柔性鉸鏈的設計分析奠定基礎。

1.1 設計變量定義

在多交叉簧片柔性鉸鏈內部，圓弧曲梁簧片的尺寸由其連接的靜剛體和動剛體決定，如圖1所示。在固定端點o處建立變形單元(element)坐標系oxeye，xe軸指向柔性鉸鏈中心O。動剛體上自由端點A的位置決定簧片的初始形狀，用OA與xe軸的夾角表示，定義為位形角αλ。

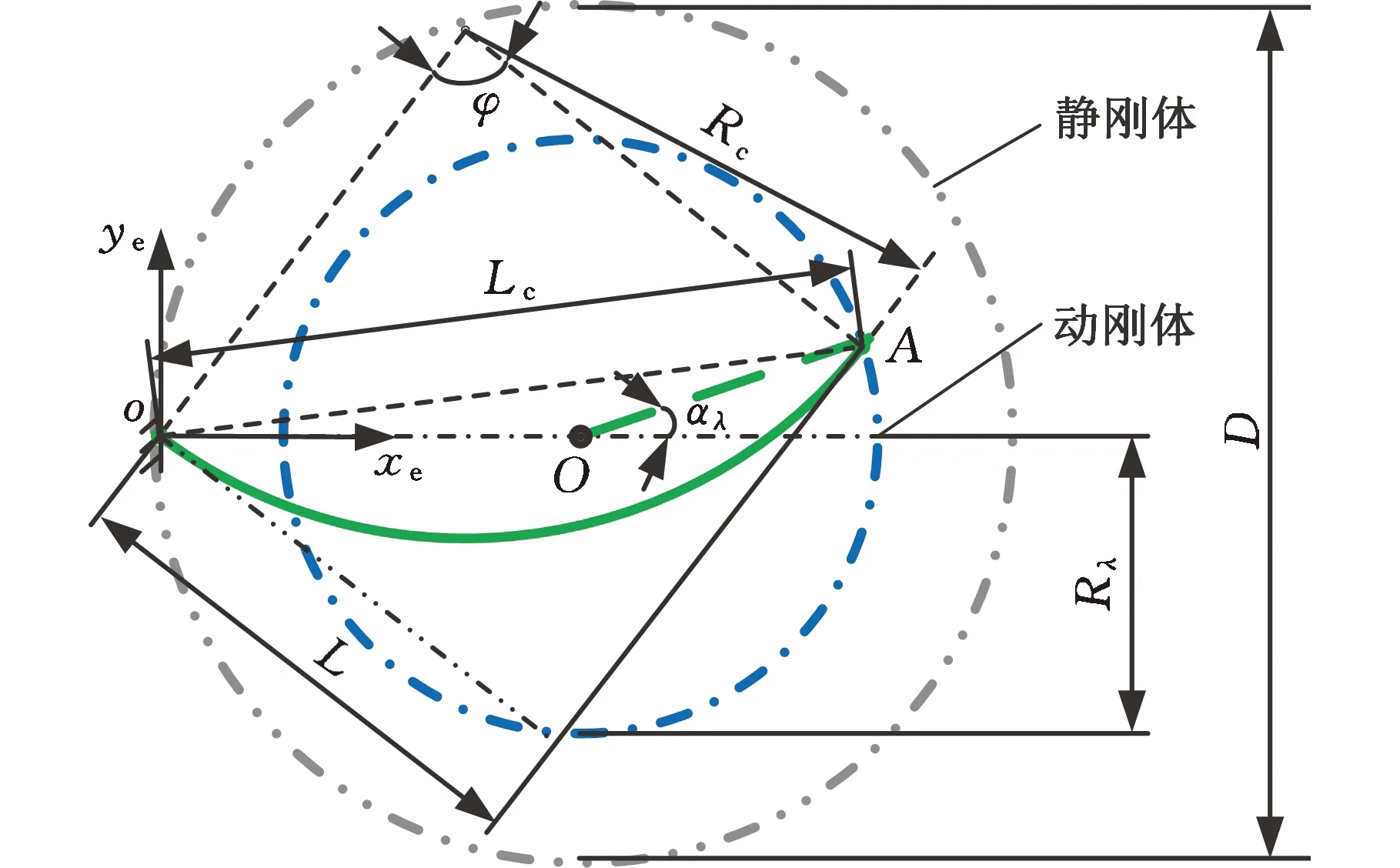
圖1 圓弧曲梁簧片結構示意圖

定義半徑系數λ以表征動、靜剛體的相對大小，進而由靜剛體直徑D確定動剛體半徑Rλ：

Rλ=0.5Dλ/(1-λ)λ∈(0,1)

(1)

簧片弦長(chord length)Lc由αλ、Rλ、D確定：

(2)

當OA長度為(Rλ+0.5D)時，簧片處于最大拉伸狀態。引入長度系數ξ(ξ>1)計算簧片弧長(arc length)La和曲率半徑(radius of curvature)Rc：

(3)

給定簧片圓心角φ，由簧片弧長La最大值確定長度系數ξ上限，得到ξ的取值范圍：

(4)

進一步根據弦長Lc與弧長La的幾何關系，得到簧片位形角αλ的取值范圍：

(5)

設OA在簧片固定端切線方向的投影長度為L(下文簡記為投影長度)，其表達式為

L=Lccos(0.5φ)

(6)

直梁簧片的圓心角為0°，即L=Lc。為避免L≤0，設置φ∈[0°,90°)。設計簧片為恒等截面，寬度為W，厚度為T。

1.2 載荷-位移關系的建立

為描述簧片的受載變形，在坐標系oxeye上建立變形坐標系oxy，x軸沿簧片固定端切線方向，x軸與xe軸的夾角為α，如圖2所示。

圖2 圓弧曲梁簧片變形

在變形坐標系oxy內，定義簧片平面載荷-彎矩M、切向力F、法向力P和平面位移-轉角θ、切向位移Δx、法向位移Δy。使用投影長度L將所有平面載荷、位移變量進行量綱一化處理：

(7)

式中，E為材料彈性模量；I為截面慣性矩。

根據梁約束模型，將位移作為自變量，得到簧片自由端的量綱一載荷-位移關系[16]：

(8)

kT=12L2/T2kp=12+p(0.2-p/700)

式中，κ為簧片量綱一曲率，κ=L/Rc=sinφ。

式(8)適用于小曲率條件(|κ|≤0.1)和中等變形條件(平面位移小于梁長的10%，|p|≤5.0)。

1.3 變形應力方程推導

在變形坐標系oxy內，圓弧曲梁上任意點的量綱一縱坐標和切向位移分別為y(x)、δy(x)。小曲率條件下，δy(x)關于量綱一法向力p的方程[16]為

(9)

式中，c1、c2、c3、c4為待定系數，|κ|≤0.1，x∈[0,1]。

基于Euler-Bernoulli梁假設，得到具有大長厚比(L/T≥10)的圓弧曲梁簧片的支配方程:

(10)

y(x)=δy(x)+0.5κx2

簧片兩端(x=0,1)的變形邊界條件[16]為

(11)

聯立式(9)～式(11)并對式(9)求導，得

(12)

圓弧曲梁簧片具有大長厚比，可視為Euler-Bernoulli梁而忽略剪應力，故簧片上任意一點的應力可近似為彎曲應力σb和軸向應力σt的疊加：

(13)

通過求解上述公式，得到簧片的變形應力分布，并確定簧片最大變形應力值及其位置。

2 柔性鉸鏈力學建模

通過在動、靜剛體之間對稱配置n個相同圓弧曲梁簧片，設計多交叉曲梁簧片柔性鉸鏈，其平面對稱軸根據簧片數量的奇偶設置于簧片1方向上或簧片1與簧片n中間方向上，如圖3a所示。

設對稱軸一側相鄰簧片的交叉半角為β，改變交叉半角和簧片數量，對應得到不同的平面對稱構型。為構建通用力學模型用于柔性鉸鏈的設計分析，首先建立其變形方程(載荷平衡方程和變形協調方程)，進而分析零軸漂轉動載荷條件以確定構型參數，并進行大變形問題求解建模。

2.1 變形方程的建立

分別在柔性鉸鏈中心O和各簧片固定端點oi(i=1,2,…,n)處建立全局坐標系OXY和局部坐標系oeixeiyei，定義xei軸與X軸夾角為相位角為γi。將柔性鉸鏈動剛體上任意位置的全部載荷集中等效為隨轉角θ變化的A0點處廣義力(M,Fx,Fy)，如圖3b所示。

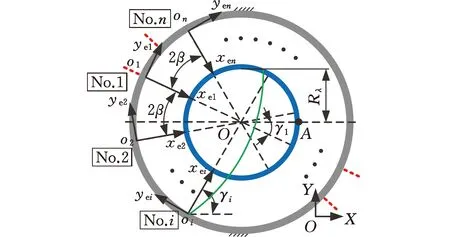
(a)平面對稱構型

設(Mi,Fi,Pi)為簧片自由端點Ai處的分配作用力，簧片變形產生的反作用力與之平衡。以動剛體中心O′為力矩平衡點，廣義力(M,Fx,Fy)在O′點的合力矩為Mz，載荷平衡方程為

(14)

M+FyRλcosθ-FxRλsinθ

(15)

k1=cos(αλ-α)k2= sin(αλ-α)

α=arcsin(Rλsinαλ/Lc)-0.5φ

式中，α為xi軸與xei軸的夾角；αλ為簧片位形角。

柔性鉸鏈的變形協調方程為

(16)

k3=cos(γi+α)k4= sin(γi+α)

式中，dx=dX/L， dy=dY/L分別為X、Y軸上量綱一軸漂分量。

2.2 零軸漂轉動載荷條件分析

當柔性鉸鏈零軸漂轉動時，各簧片變形和受力大小相同，簧片自由端的相同量綱一法向力和切向力分別為p和f，由式(8)求解。簡化式(14)后得到零軸漂轉動載荷條件：

(17)

相同位移條件下，量綱一曲率決定p和f的大小進而影響廣義力(Fx,Fy)的相對大小。由式(8)可知，p和f不能同時為0，故式(17)中(Fx,Fy)皆為0時，簧片i相位角γi需滿足條件：

γi=2(i-1)β+γ1β=π/n

(18)

式中，γ1為簧片1相位角；n為簧片總數。

在此條件下，柔性鉸鏈平面構型表現出全對稱特性，即簧片在圓周方向上均勻分布。此時，(Fx,Fy)作為干擾力，影響柔性鉸鏈轉動精度。

無干擾力作用時，轉矩M為驅動力矩，柔性鉸鏈的所有簧片相同時，不同的簧片1相位角γ1和簧片結構形式在理想情況下不影響轉動精度；有干擾力作用時，通過簧片總數n的奇偶取值和簧片1相位角γ1的合理設置，令對稱軸方向與干擾力方向重合，以利用對稱性[19]減弱其影響。

2.3 大變形問題求解建模

梁約束模型采用了變形曲率的線性近似，當梁產生大變形(末端位移大于梁長的10%)時不再適用。采用鏈式梁約束(CBCM)模型[17]進一步擴展建模，通過梁的均等離散化處理(圖4)，減小曲率的近似誤差，以實現多交叉大曲率簧片柔性鉸鏈大變形分析問題的精確求解。

圖4 圓弧曲梁簧片離散化示意圖[17]

在坐標系oixiyi內，簧片i的自由端點坐標為(Xi,Yi)，傾角為θi。在簧片i中單元j(j=1,2,…,N)的節點j-1處，沿切線方向建立局部坐標系oijxijyij。將變形前xij軸與xi軸的夾角記為αij，產生變形(deformation)后的夾角記為αdij,相關計算式為

(19)

αdi1=0αdij=αij+θi-θijj=2,3,…,N

(20)

式中，θ為柔性鉸鏈轉角。

將簧片i中單元j自由端的待求解量綱一載荷和位移變量分別記為(mij,fij,pij)、(δyij,δxij,θij)，單簧片i的總變量數為6N，需要建立6N個求解方程。

在CBCM建模過程中，所分析的圓弧曲梁簧片仍屬于Euler-Bernoulli梁，每個離散單元皆適用于上述變形建模理論。

對每個離散單元應用式(8)，建立3N個方程。由簧片圓心角φ∈[0， 90°)確定κ∈[0,1]，為保證每個離散單元的量綱一曲率|κ|≤0.1，取N=10。利用CBCM模型理論建立剩余3N個方程[17]。

(1)靜態平衡方程(共3N-3個方程)為

(21)

(2)幾何約束方程(共3個方程)為

(22)

將工作載荷或位移代入式(14)～式(16)，并對各柔性鉸鏈簧片列上述6N個方程，聯立求解得到各載荷和位移變量。變量代入后求解式(12)、式(13)，得到各簧片應力分布和最大應力。

3 模型驗證

通過仿真和實驗相結合，對比分析多交叉直梁、曲梁簧片柔性鉸鏈的轉動剛度和最大應力，驗證上述理論模型的準確性，并根據分析結果檢驗多交叉曲梁簧片柔性鉸鏈在減小轉動剛度和最大應力方面的實際效果。

3.1 柔性鉸鏈試件設計

為消除翹曲變形，采用兩組三交叉簧片柔性鉸鏈鏡像對稱組合得到柔性鉸鏈試件。簧片和動、靜剛體設計為可拆卸分體式結構，如圖5所示。試件的靜剛體直徑D=56 mm，半徑系數λ=0.5。

圖5 柔性鉸鏈試件

試件采用3D打印加工，簧片設計參數如下。簧片材料：聚乳酸(PLA)，彈性模量E=3.7 GPa，泊松比μ=0.35，屈服極限δs=58 MPa。曲梁簧片設計尺寸：曲率半徑Rc=70 mm，位形角αλ=10°，量綱一曲率κ≈0.730 95；對比直梁簧片設計尺寸：長度L=D，αλ= 0，κ= 0；恒定矩形截面尺寸：寬度W=5 mm，厚度T=1 mm。

3.2 實驗平臺和測試方案設計

柔性鉸鏈測試實驗平臺主要由法蘭扭矩傳感器 (量程0～1000 N·mm，綜合精度0.1%F.s)、精密XYR三軸位移平臺、智能數顯儀以及固定支架組成，如圖6所示。通過調整XY位移平臺，減小柔性鉸鏈安裝的軸線對齊誤差。

圖6 柔性鉸鏈實驗平臺

根據扭矩傳感器精度，設置一組連續預設轉角集，通過手動調整R軸轉角θ給平臺上柔性鉸鏈施加轉矩。對比測試多交叉直、曲梁簧片柔性鉸鏈，記錄各預設轉角θ對應測得的數顯儀轉矩示數M，4次測量取平均值，得到M-θ關系曲線。

由于簧片應力難以實際測量，故采用非線性有限元仿真方法計算柔性鉸鏈的最大應力σmax。首先，對比實驗測試與Abaqus仿真(六面體網格劃分)計算得到的M-θ曲線，驗證仿真模型的準確性，再利用仿真模型得到σmax-θ關系曲線。

3.3 實驗結果及分析

轉矩實驗結果(圖7)顯示，多交叉曲梁簧片柔性鉸鏈平均轉動剛度(174.75 N·mm·rad-1)低于多交叉直梁簧片柔性鉸鏈(550.04 N·mm·rad-1)。轉矩仿真結果(圖8)驗證了仿真模型的準確性。

應力仿真結果(圖9)顯示，曲梁簧片的σmax在θ∈[0,4.2°]時高于直梁簧片的σmax，但在θ>4.2°時遠低于直梁簧片的σmax。θ∈[11°,18°]時，曲梁簧片的σmax基本不變，但當θ>18°時σmax開始線性增大。從應力分布情況來看，θ∈[0,11°]時，曲梁簧片σmax產生在其固定端根部，當θ>11°時轉移至簧片中部。相比之下，直梁簧片的σmax保持在中部。

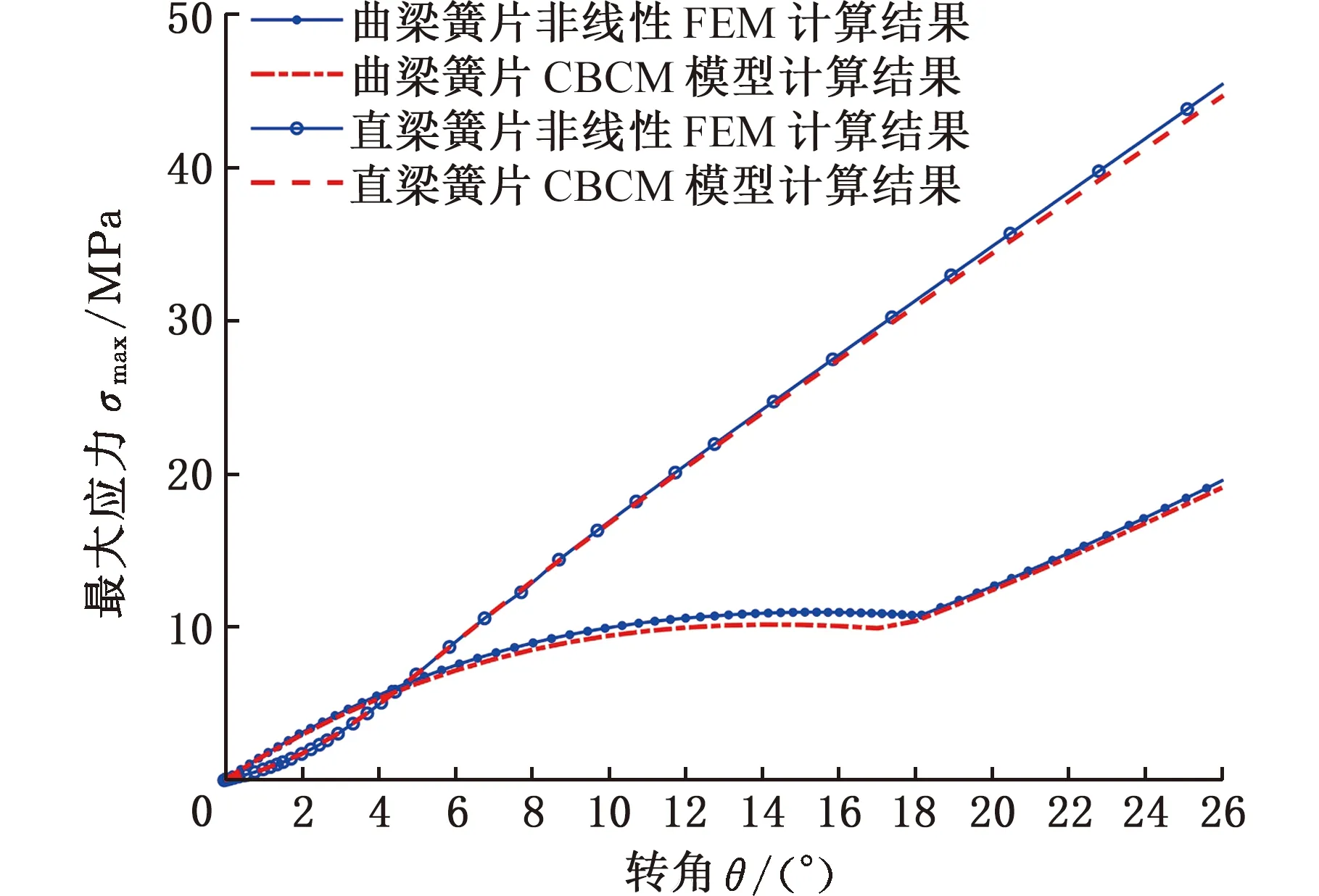
圖9 最大應力仿真與理論模型結果對比

實驗測試、非線性FEM仿真與理論模型計算結果基本一致，驗證了理論模型的準確性。θ=26°時，直、曲梁簧片柔性鉸鏈轉矩實驗測試與理論計算結果的相對誤差分別為1.12%、5.57%，主要誤差來源為試件幾何和裝配誤差，使得部分簧片在長度方向存在殘余壓/拉應力，從而使剛度減小/增大。

4 柔性鉸鏈性能的理論計算分析

為優化柔性鉸鏈的參數組合，基于理論模型分析半徑系數λ、量綱一曲率κ和位形角αλ對柔性鉸鏈性能(轉矩M、最大應力σmax隨轉角θ的變化規律)的影響。分析時選取的靜剛體直徑、簧片材料和寬度與上文實驗設置相同。

4.1 半徑系數λ的影響

設量綱一曲率κ和位形角αλ皆為0，厚度T取值范圍為0.6～1.2 mm，分析不同半徑系數λ對轉矩M和最大應力σmax的影響，λ∈[0.1273,0.5]。

固定轉角θ和厚度T，隨λ的增大，最大應力σmax、轉矩M皆減小并且在小轉角、小厚度條件下線性減小。固定λ，σmax與T成線性正相關，M與T成非線性正相關，如圖10、圖11所示。當柔性鉸鏈簧片厚度T確定時，半徑系數λ取0.5，以獲得低轉動剛度和大轉角范圍。

4.2 量綱一曲率κ的影響

設定半徑系數λ=0.5，繼續取簧片位形角αλ為0，厚度T取值范圍為0.5～1.5 mm，分析不同量綱一曲率κ對轉矩M和最大應力σmax的影響。

固定轉角θ和厚度T，隨κ的增大，M、σmax皆先減小后增大，且各對應在[0,1]中存在唯一κ值使M或σmax取極小值，分別記為轉矩極小值曲率κM和應力極小值曲率κσ，如圖12、圖13所示。

圖12 轉矩隨量綱一曲率的變化關系

圖13 最大應力隨量綱一曲率的變化關系

轉矩極小值曲率κM、應力極小值曲率κσ與轉角θ成正相關，但與厚度T無關。固定θ時，κ的取值不影響M、σmax與T的相關性。

當柔性鉸鏈最大設計轉角θmax確定時， 量綱一曲率κ在θmax確定的κM和κσ之間選取，以同時減小轉動剛度和最大應力。

4.2 位形角αλ的影響

為便于比較，設定厚度T=1 mm，繼續取半徑系數λ=0.5，分析不同位形角αλ對轉矩M和最大應力σmax的影響(αλ根據式(5)計算選取)，結果如圖14、圖15所示。

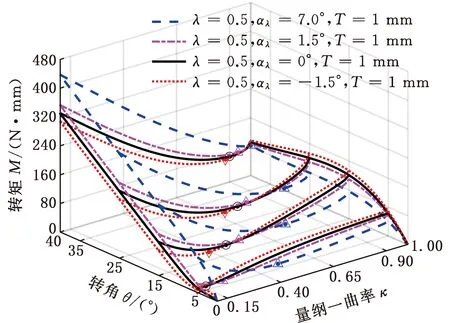
圖14 轉矩隨位形角的變化關系

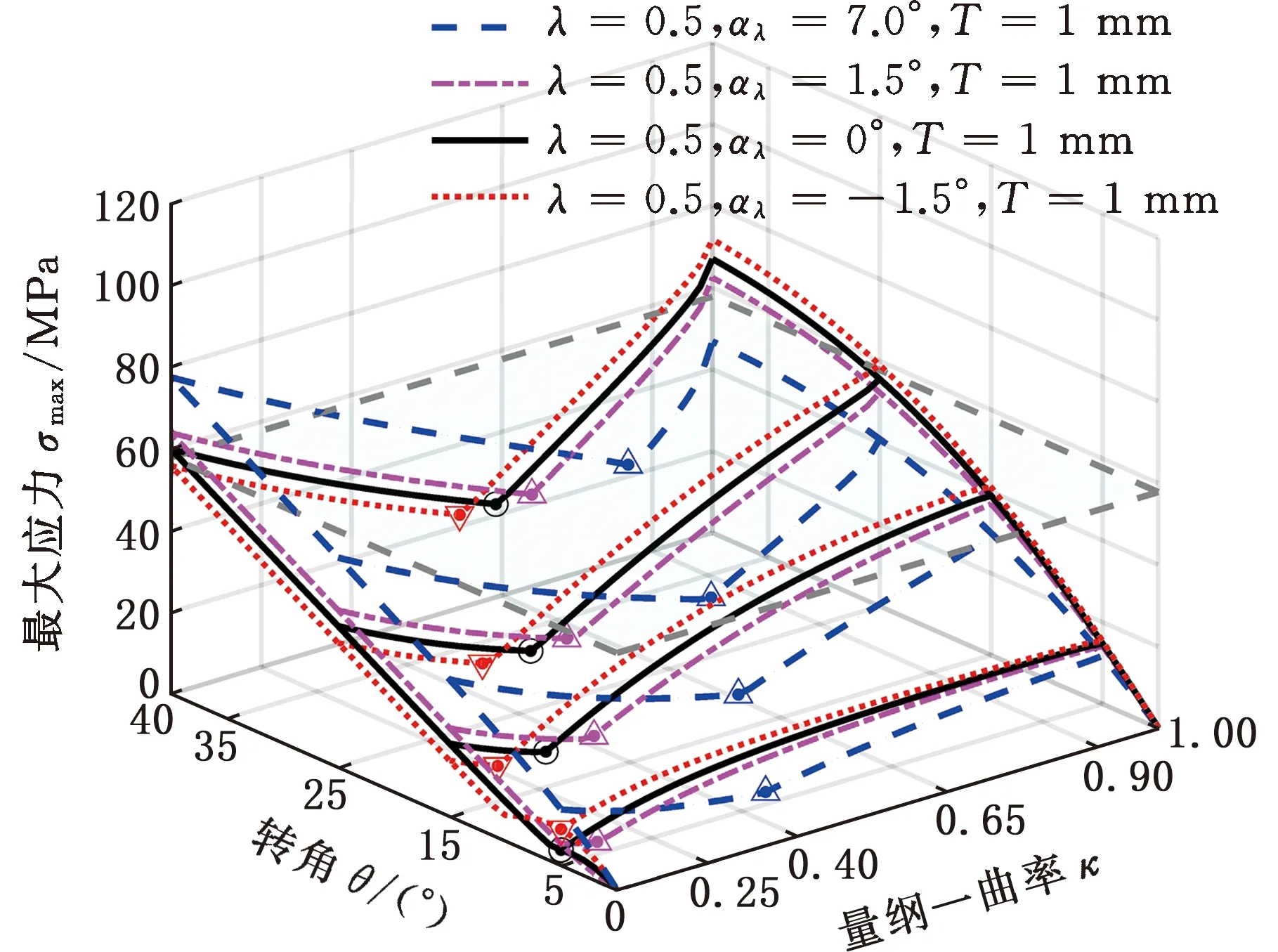
圖15 最大應力轉矩隨位形角的變化關系

固定轉角θ和厚度T，轉矩極小值曲率κM、應力極小值曲率κσ、轉矩M和最大應力σmax皆受位形角αλ的正負取值影響(相比αλ=0)：

當αλ=-1.5°時，κM、κσ皆減小；量綱一曲率κ以κM為界向上或向下取值時，對應轉矩M增大小或減小；量綱一曲率κ以κσ為界向上或向下取值時，最大應力σmax增大或減小。αλ=1.5°時的參數影響規律與αλ=-1.5°時完全相反。

進一步增大αλ，當αλ=7°,κ=1時，轉矩M、最大應力σmax皆減小，而且在15°～37°轉角范圍內M幾乎恒定，即柔性鉸鏈獲得零剛度特性[20]。

當設計簧片位形角|αλ|較小時，隨θ的增大，通過改變量綱一曲率κ易獲得轉矩M在某一轉角范圍內減小，即柔性鉸鏈獲得負剛度特性。

當柔性鉸鏈最大設計轉角θmax確定時，先根據式(5)選取負位形角-αλ以進一步增大行程，再在(θmax,-αλ)確定的κM和κσ之間選取量綱一曲率κ，以同時減小轉動剛度和最大應力，獲得相對更小的傳輸剛度[21](即最大許用應力內的轉動剛度)和更大轉角范圍。

當有零剛度或負剛度特性的柔性鉸鏈設計需求時，優先選取κ=1，并通過調整αλ完成具體剛度特性的參數設計。

4 結論

(1)本文提出了一種多交叉曲梁簧片柔性鉸鏈，建立其大變形理論分析模型并通過實驗驗證，探究了不同設計變量取值對其性能的影響。

(2)所設計的柔性鉸鏈能通過不同半徑系數λ、簧片量綱一曲率κ和位形角αλ的參數組合獲得正剛度特性、零剛度特性和負剛度特性。特別地，當αλ=7°,κ=1時，設計柔性鉸鏈實現了22°大行程恒定轉矩運動。

(3)本文研究的多交叉曲梁簧片柔性鉸鏈及其參數性能分析結果，為大行程、低剛度、高精度多交叉簧片柔性鉸鏈的設計提供了新的思路和參考。后續將研究其他曲梁簧片結構的變形特性以用于設計新型大行程柔性鉸鏈，并進一步提升其承載能力以適應大負載應用需求。