分組密碼最小活躍S 盒個數快速搜索算法

劉正斌，李永強，朱朝熹

（1.保密通信重點實驗室，四川 成都 610041；2.中國科學院信息工程研究所，北京 100093）

0 引言

差分密碼分析[1]和線性密碼分析[2]是密碼分析中最有效的2 種分析方法，抵抗差分密碼分析和線性密碼分析是現代分組密碼最基本的一項設計準則。評估分組密碼抵抗差分密碼分析和線性密碼分析的主要方法包括計算最大差分/線性特征的概率和計算最小活躍S 盒個數。對于代入置換網絡（SPN,substitution permutation network）型分組密碼，根據寬軌跡設計策略[3]，可以得到抵抗差分密碼分析和線性密碼分析的可證明安全界。通過計算最小活躍S 盒個數，并結合S 盒的最大差分概率和線性概率，設計者可以計算出最大差分特征概率和線性特征概率的上界。目前，學術界已經提出了一些自動化搜索算法來輔助評估分組密碼的安全性。

1994 年，Matsui[4]提出一種分支定界搜索算法來自動化搜索分組密碼DES（data encryption standard）的最優差分特征和線性特征，該算法也稱Matsui 算法。盡管該算法能夠在有限時間內找到DES 的16 輪最優差分特征和線性特征，但是對于其他一些分組密碼，它的效率卻非常低。隨后，Ohta 等[5]和Aoki 等[6]分別改進了Matsui 算法，找到了分組密碼 FEAL（fast data encipherment algorithm）的最優差分特征和線性特征。雖然Matsui 算法可以擴展到搜索SPN 型分組密碼的最優差分特征和線性特征，但是其線性層的快速擴散性質和雪崩效應嚴重降低了搜索效率。對于使用比特置換層的SPN 型分組密碼，Arnaud 等[7]優化了Matsui 算法并找到了分組密碼PRESENT、PUFFIN 和ICEBERG 的全輪最優差分特征。Ji 等[8]則通過引入3 種加速方法來提高Matsui 算法的搜索效率，并找到了DESL 和GIFT 約減輪數的最優差分特征和線性特征。Kim 等[9]改進了Matsui 算法來搜索SPN 型分組密碼的最優差分特征和線性特征。

2011 年，Mouha 等[10]提出了一種基于混合整數線性規劃（MILP,mixed integer linear programming）的方法來搜索SPN 型分組密碼的最小活躍S 盒個數。Sun 等[11]將基于MILP 的方法擴展到使用比特置換層的分組密碼，提出了2 種能夠精確刻畫S 盒的差分和掩碼傳播的方法，即邏輯條件模型和凸包計算，并給出了約減不等式組的貪婪算法。Abdelkhalek 等[12]將邏輯條件模型中約束條件的生成問題轉化成布爾函數的和積的最小化問題，并使用Quine-McCluskey 算法[13-14]和Espresso 算法[15]來建立8 bit S 盒的差分分布表的比特模型。為了提高基于MILP 方法的效率，Zhang 等[16]在MILP 模型中引入了分支定界策略來減少約束條件，降低搜索空間；Zhou 等[17]則使用分而治之的方法來優化模型求解。近幾年，基于MILP 的方法被廣泛應用于分組密碼的設計與分析中[18-30]。

除了算法模型的優化外，基于MILP 方法的效率主要由求解器的效率決定，如CPLEX、Gurobi等。對于輪數較長或者輪函數較復雜的分組密碼，由于需要更多的變量和不等式來描述差分和掩碼的傳播，因此求解器通常需要執行非常長的時間來得到最優解。對于攻擊一個已知的分組密碼，花費十幾天甚至幾個月的時間是有意義的。然而，從分組密碼設計的角度，為了優化密碼部件（S 盒、擴散矩陣等）的選擇以及確定合理的迭代輪數，設計者通常需要進行多次安全性評估。因此，一個快速搜索最小活躍S 盒個數的算法對于評估分組密碼抵抗差分密碼分析和線性密碼分析的安全性具有重要意義，在分組密碼設計過程中具有重要實用價值。

本文主要的研究工作如下。

1) 提出了擴散矩陣的差分/掩碼模式分布表的概念。對于二元域矩陣，證明了通過遍歷輸入差分/掩碼方式來構造差分/掩碼模式分布表的計算復雜度的下界。基于該下界，給出了構造差分/掩碼模式分布表的快速方法。

2) 對于任意階最大距離可分（MDS,maximum distance separable）矩陣，證明了滿足分支數條件的差分/掩碼模式一定能夠實例化，即對于特定的差分/掩碼模式，一定存在對應的差分/掩碼傳播。基于分支數關系，給出了任意階MDS 矩陣的差分/掩碼模式的傳播集合。

3) 基于差分/掩碼模式分布表，提出了一種自動化搜索分組密碼最小活躍S 盒個數的快速算法。針對SPN 型分組密碼，通過實驗驗證了該算法的有效性。實驗結果表明，本文算法效率比目前常用的基于MILP 的方法高。

1 差分/掩碼模式分布表

1.1 差分/掩碼模式分布表定義

對于雙射S 盒，設ΔX和ΔY分別表示S 盒的輸入差分模式和輸出差分模式，則ΔY=0當且僅當ΔX=0，ΔY=1當且僅當ΔX=1，反之亦然。

對于線性變換y=Ax，A是一個n階矩陣，設輸入差分 為 Δx=(Δx1,…,Δxn)，則輸出差分為Δy=AΔx。令 ΔX=(ΔX1,…,ΔXn)表示輸入差分模式，ΔY=(ΔY1,…,ΔYn)表示輸出差分模式，那么(ΔX,ΔY)就稱為線性變換的一個差分模式傳播。

定義4差分模式分布表。線性變換的差分模式分布表（DPDT,difference pattern distribution table）是一個表示其輸入差分模式和輸出差分模式的分布表。對于給定的輸入差分模式ΔX=(ΔX1,…,ΔXn) ∈和輸出差分模式ΔY=(ΔY1,…,ΔYn) ∈，令α= ΔX1‖…‖ ΔX n，β= ΔY1‖…‖ ΔY n，那么差分模式分布表中第α行、第β列元素DPDT(α,β)=1表示一定存在與(ΔX,ΔY)對應的差分傳播(Δx,Δy)，滿 足Pr(Δx→ Δy) ≠0，其中，Pr(·)表示概率。

與差分模式分布表對應，可以定義線性變換y=Ax的掩碼模式分布表。記輸入掩碼為Γx=(Γx1,…,Γxn)，那么輸出掩碼為 Γy=(AT)-1Γx。令ΓX=(ΓX1,…,ΓXn)表示輸入掩碼模式，ΓY=(ΓY1,…,ΓYn)表示輸出掩碼模式，那么(ΓX,ΓY)就稱為線性變換的一個掩碼模式傳播。

定義5掩碼模式分布表。線性變換的掩碼模式分布表（MPDT,mask pattern distribution table）是表示其輸入掩碼模式和輸出掩碼模式的分布表。對于給定的輸入掩碼模式 ΓX=(ΓX1,…,ΓXn) ∈和輸出差分模式ΓY=(ΓY1,…,ΓYn) ∈，令μ= ΓX1‖…‖ ΓX n，ν= ΓY1‖…‖ ΓY n，那么掩碼模式分布表中第μ行、第ν列元素MPDT(μ,ν)=1表示一定存在與(ΓX,ΓY)對應的掩碼(Γx,Γy)，滿足

接下來，針對分組密碼中最常用的2 種擴散矩陣——MDS 矩陣和二元域矩陣，給出其差分模式分布表和掩碼模式分布表的構造。

1.2 MDS 矩陣差分/掩碼模式分布表構造

首先證明MDS 矩陣的差分/掩碼模式傳播與其分支數之間的等價關系，然后基于分支數來構造MDS矩陣的差分/掩碼模式分布表。

設m為正整數，為包含2m個元素的有限域。GLn()表示元素取自有限域上的n階可逆矩陣的集合。對于Fq上的MDS 碼，其碼字分布有如下結果。

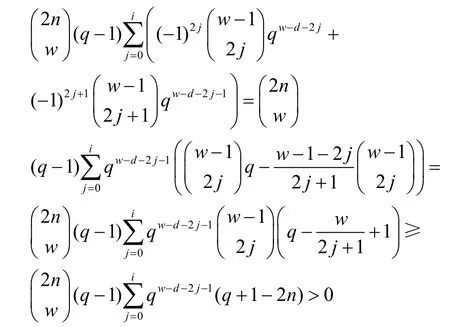
如果存在i，使w-d=2i，此時根據上述證明情況可得

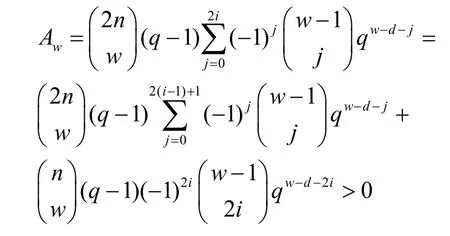
綜上，定理2 證畢。

根據定理2，MDS 矩陣的差分/掩碼模式分布表可以直接根據其分支數來構造。該方法只需要遍歷差分/掩碼模式，極大降低了差分/掩碼模式分布表的計算復雜度，對于上n階MDS 矩陣，計算復雜度從 O(2mn)降為 O(2n)。

1.3 二元域矩陣差分/掩碼模式分布表構造

對于二元域矩陣，首先證明通過遍歷輸入差分/掩碼來構造差分/掩碼模式分布表的計算復雜度的下界，然后給出差分/掩碼模式分布表的構造方法。

根據定理3，對于分組密碼中常用的任意4 階和8 階二元域矩陣，構造其差分/掩碼模式分布表的計算復雜度分別為 O(212)和O (232)，因此可以在計算機上非常快速地構造。然而，構造16 階二元域矩陣的差分/掩碼模式分布表需要 O (280)的計算量，因此無法通過這種方式直接構造。二元域矩陣差分模式分布表的構造如算法1 所示。在算法1 中，對于4 階和8 階二元域矩陣，d的值分別為3 和4。

算法1二元域矩陣差分模式分布表構造算法

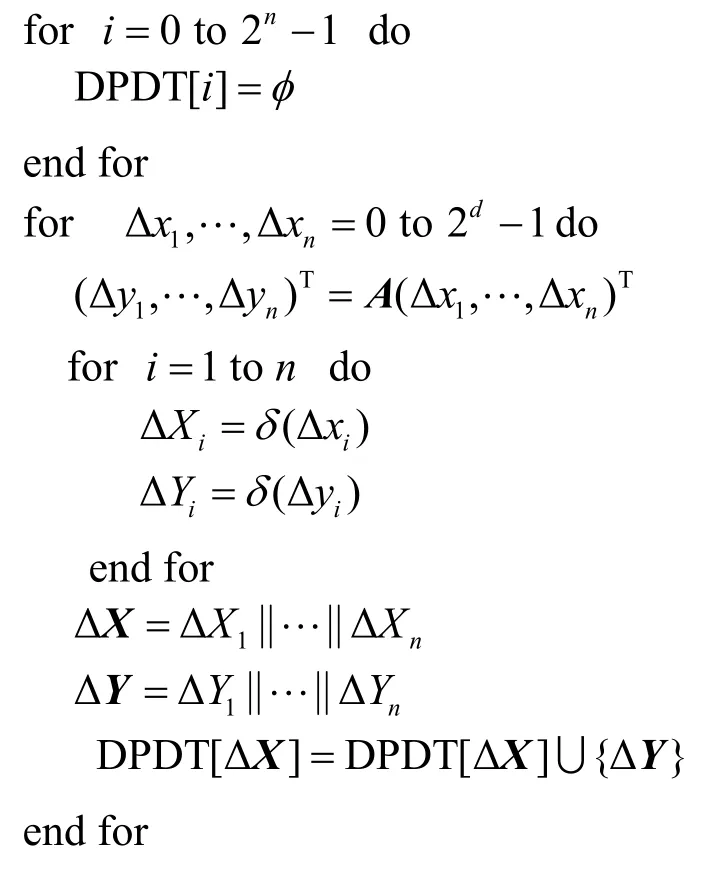
對于差分模式分布表的每一行，按照漢明重量從小到大的順序對輸出差分模式進行排序。掩碼模式分布表的構造是類似的，只需要將其中的矩陣A替換為矩陣 (AT)-1。

2 SPN 型分組密碼活躍S 盒個數搜索算法

2.1 分支定界搜索算法

Matsui 算法對差分特征和線性特征執行遞歸搜索，它根據已知的i輪最優特征概率Bi（1 ≤i≤r-1）和r輪最優特征概率Br的初始估計值來計算Br。對于任意，只要≤Br，Matsui算法一定可以得到r輪最優特征概率Br。對于Feistel密碼，其輪函數的差分傳播過程如圖1 所示，其中，F表示輪函數中的一個變換。Matsui 算法搜索最優差分特征的偽代碼如算法2 所示。

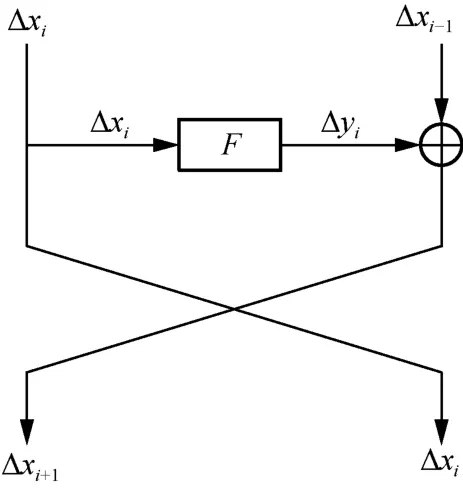
圖1 Feistel 密碼輪函數的差分傳播過程

算法2Matsui 算法搜索最優差分特征

2.2 SPN 型分組密碼最小活躍S 盒個數搜索算法

SPN 結構是現代分組密碼最常用的一種密碼結構，其輪函數包含一個非線性替換層和一個線性擴散層。非線性替換層又稱S 盒層，它使用一組并行的S 盒；線性擴散層是一個線性函數，通常包含一個基于字的置換和一個基于矩陣乘法的線性變換。SPN 型分組密碼最著名的實例是高級加密標準（AES,advanced encryption standard），它的輪函數包含字節置換（SubBytes）、行移位（ShiftRows）、列混淆（MixColumns）、輪密鑰加（AddRoundKey）。

在輕量級密碼領域，研究者提出了若干SPN 型輕量級分組密碼。為了適用于資源受限環境，S 盒層通常使用4 bit S 盒，列混淆層則使用輕量級MDS矩陣或者二元域矩陣。不失一般性，本文仍然沿用AES 的輪函數結構，使用符號SB 表示S 盒層，SR表示線性置換層，MC 表示列混淆層，AK 表示輪密鑰加。SPN 型分組密碼的輪函數如圖2 所示，其中，S 表示S 盒變換。

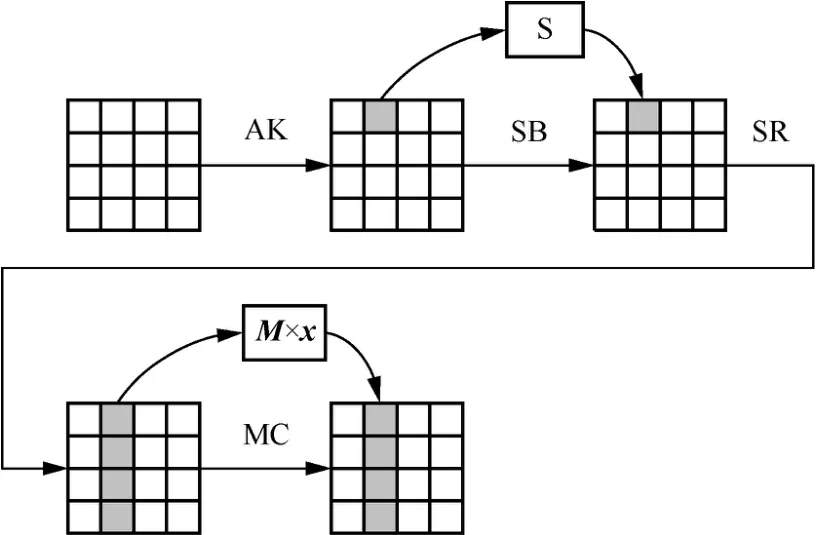
圖2 SPN 型分組密碼的輪函數

為了進一步提高搜索效率，算法3 引入了一些優化策略。

首先，按照漢明重量從小到大的順序遍歷明文差分模式，一旦某個漢明重量的差分模式不滿足搜索條件，即n1+Br-1＞Br，就停止搜索，不需要遍歷更高漢明重量的明文差分模式。這種策略使搜索空間非常小——只包含低漢明重量的差分模式，極大地提高了算法效率。

另外，由于差分模式分布表的輸出差分模式按照漢明重量從小到大的順序排列，對于給定的輸入差分模式，每次查表都得到當前漢明重量最小的輸出差分模式，即下一輪的活躍S 盒個數，可以更有效地排除不滿足條件的差分模式。一旦某個輸出差分模式不滿足搜索條件，就可以提前停止，不需要繼續搜索下一輪。

3 本文算法應用

將本文算法應用于SPN 型分組密碼LED（Light encryption device）[32]、SKINNY[27]、CRAFT[28]以及認證加密算法FIDES[29]，找到了其全輪最小活躍S 盒個數的下界。對于隨機選擇的S 盒，該下界是緊致的，即對于一個特定的S 盒，可以構造一條有效的差分/線性特征。實驗結果如表1～表4 所示，其中，#SD和#SL分別表示差分活躍S 盒個數和線性活躍S 盒個數，TOurA和TMILP分別表示本文算法和基于MILP方法的運行時間，—表示未給出或者未找到相應輪數的結果。與基于MILP 的方法相比，本文算法效率更高。

表1 LED 最小活躍S 盒個數

本文中所有實驗都是在計算機上運行的，所用的實驗平臺是Intel Core i7-6700 CPU @3.4 GHz，16 GB RAM，軟件采用VS2010，C 語言編程。

3.1 LED 分組密碼

LED 是Guo 等[32]在CHES 2011 會議上提出的一組64 bit 分組密碼，它包含2 個版本，即LED-64和LED-128，對應的密鑰長度分別為64 bit 和128 bit。由于LED 的列混淆層使用MDS 矩陣，根據寬軌跡策略，可以證明LED 任意連續4 輪的最小活躍S盒個數為25 個。

本文通過自動化搜索程序找到了LED-64 和LED-128 全輪的最小活躍S 盒個數。對于LED-64，找到差分和線性活躍S 盒一共需要134 s。對于LED-128，找到差分和線性活躍S 盒一共需要201 s。實驗結果如表1 所示，由于差分活躍S 盒與線性活躍S 盒個數相同，表1 僅列出了最小差分活躍S盒個數。表1 中r輪的時間是指在已知r-1 輪最小活躍S 盒個數的條件下，搜索r輪最小活躍S盒個數的時間，因此總的搜索時間是累積前r輪的時間。

3.2 SKINNY 分組密碼

在CRYPTO 2016 會議上，Beierle 等[27]提出了一簇可調輕量級分組密碼SKINNY，它包含2 種分組長度：64 bit 和128 bit，分別記為SKINNY-64和SKINNY-128。為了評估SKINNY 抵抗差分密碼分析和線性密碼分析的安全性，設計者使用基于MILP 的方法來搜索最小活躍S 盒個數，并找到了22 輪最小差分活躍S 盒個數，以及23 輪最小線性活躍S 盒個數。對于更多輪數，由于MILP求解器的運行時間太長，他們只提供了最小活躍S盒個數的上界。

本文找到了SKINNY 全輪的最小活躍S 盒個數，其中，搜索40 輪最小差分活躍S 盒個數需要10 s，最小線性活躍S 盒個數需要5 s，與基于MILP的方法相比效率非常高。實驗結果如表2 所示。由于SKINNY-64 和SKINNY-128 使用相同的二元域矩陣（分別作用在和上），根據定理3，SKINNY-64 和SKINNY-128 的差分/掩碼模式分布表相同，因此它們具有相同的活躍S 盒個數。

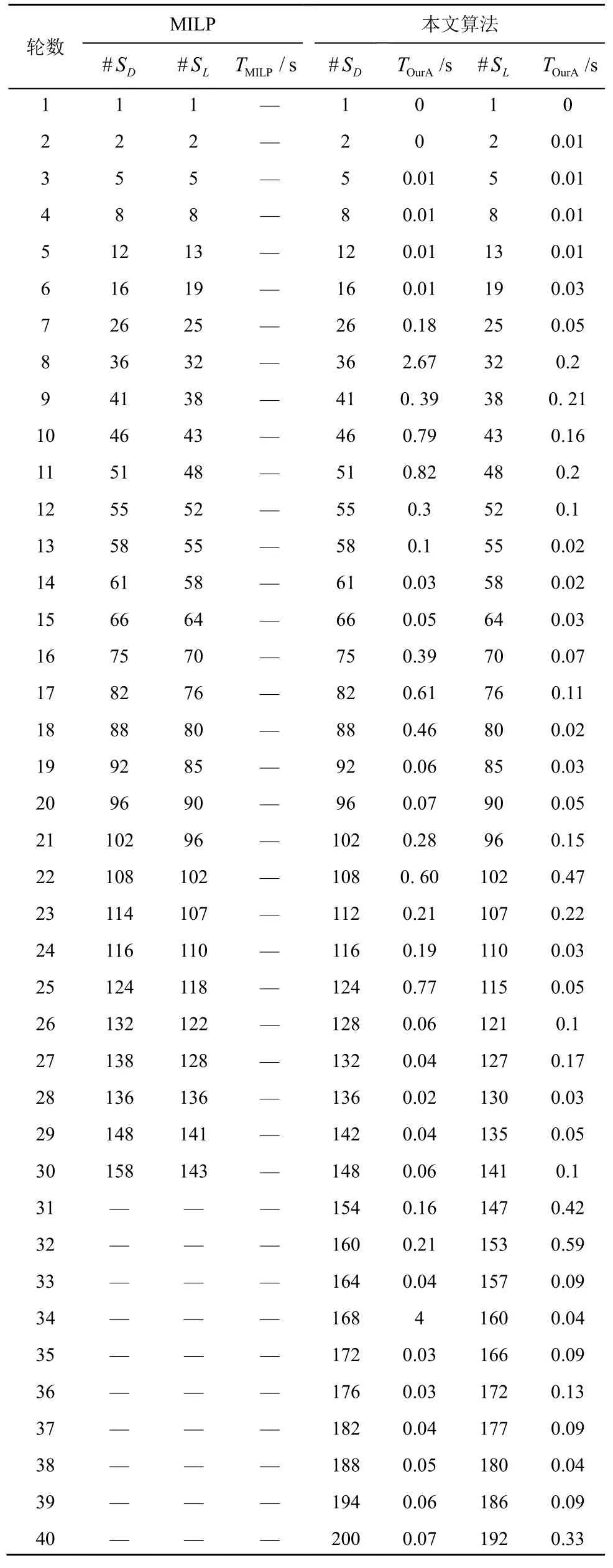
表2 SKINNY 最小活躍S 盒個數

3.3 CRAFT 分組密碼

CRAFT 是Beierle 等[28]提出的一個可調輕量級分組密碼，其分組長度為64 bit，密鑰長度為128 bit，迭代輪數為31 輪。它的設計目標是實現對差分故障攻擊的有效防護，以及以很少的額外代價同時實現加密和解密。為此，CRAFT 使用了對合的密碼部件，并且沒有使用密鑰擴展算法。在算法分析方面，設計者同時使用Matsui 算法和基于MILP 的方法來評估其抵抗差分密碼分析和線性密碼分析的安全性，得到了17 輪最小差分活躍S 盒個數的下界。

本文找到了CRAFT 全輪的最小活躍S 盒個數，算法運行時間約為2 s，實驗結果如表3 所示。由于CRAFT 使用對合的二元域矩陣，差分模式分布表和掩碼模式分布表相同，因此差分活躍S 盒個數與線性活躍S 盒個數相同，表3 只列出了最小差分活躍S 盒個數。另外，與算法設計者直接使用Matsui算法相比，本文的優化策略對于Matsui 算法的效率提升非常明顯。

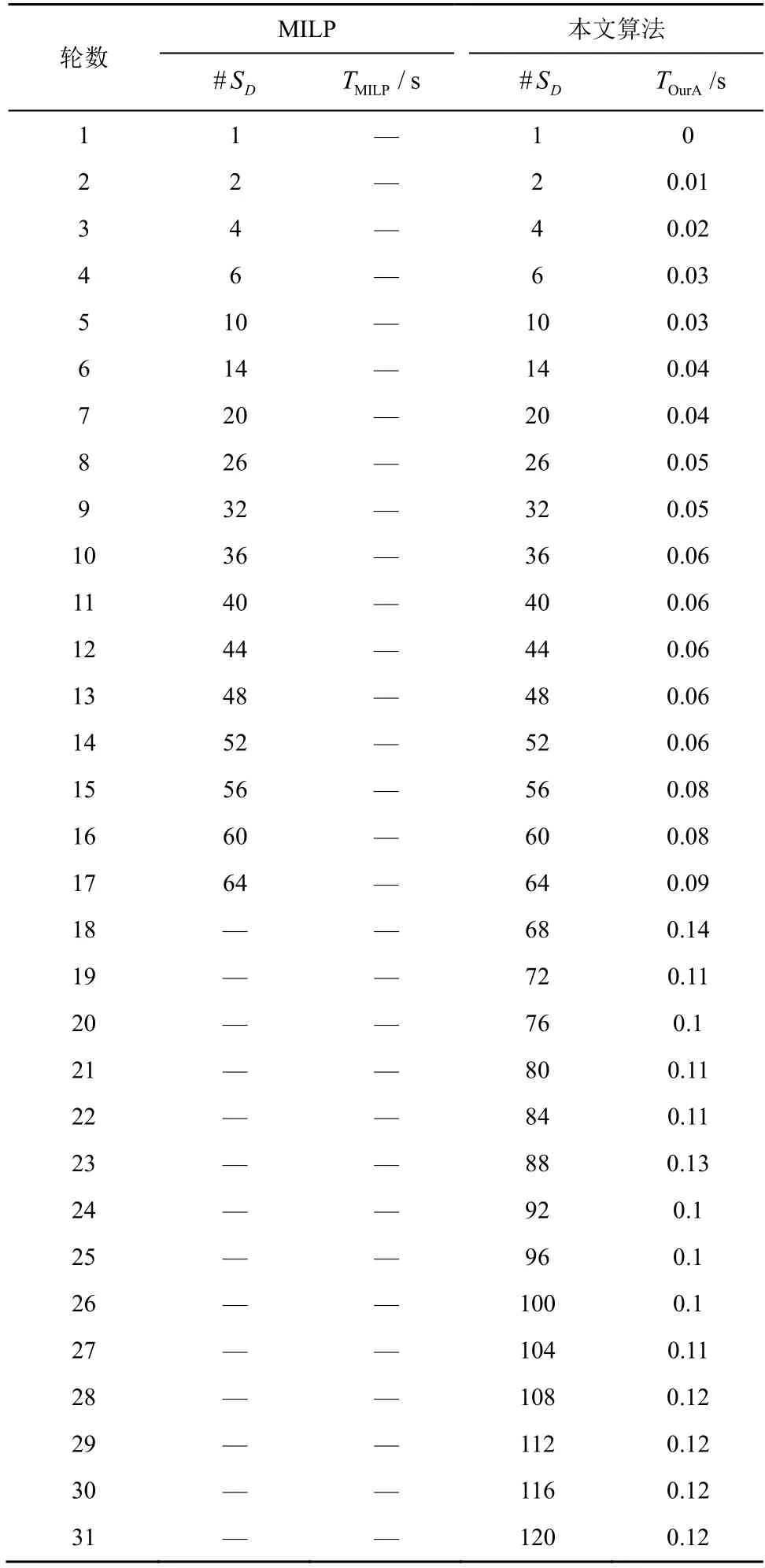
表3 CRAFT 最小活躍S 盒個數

3.4 FIDES 認證加密算法

FIDES 是面向硬件的輕量級認證加密算法[29]，采用類似Duplex Sponge 結構和專門設計的內部置換。FIDES 包含2 個版本：FIDES-80 和FIDES-96，其內部狀態分別為160 bit 和192 bit。FIDES 的加密算法采用SPN 結構，S 盒分別使用5 bit 的AB（almost bent）函數和6 bit 的APN（almost perfect nonlinear）函數，其初始化和生成標簽的過程分別執行16 次輪函數迭代。

根據寬軌跡設計策略，FIDES 的任意連續4 輪至少有16 個活躍S 盒。為了得到更好的安全界，設計者使用基于MILP 的方法搜索最小活躍S 盒個數，并找到了8 輪最小活躍S 盒個數。然而，該MILP 模型并沒有精確刻畫列混淆矩陣的差分/掩碼模式傳播，因此無法保證5～8 輪最小活躍S 盒個數的下界是緊致的。

本文找到了FIDES 全輪的最小活躍S 盒個數，由于本文通過遍歷列混淆矩陣的輸入差分/掩碼來計算其所有可能的差分/掩碼模式傳播，因此得到了最小活躍S 盒個數的緊致下界，實驗結果如表4 所示。由于列混淆層使用對合二元域矩陣，其差分模式分布表和掩碼模式分布表相同，因此差分活躍S盒個數與線性活躍S 盒個數相同，表4 只列出了最小差分活躍S 盒個數。另外，根據定理3，FIDES-80和FIDES-96 的差分/掩碼模式分布表相同，因此具有相同的活躍S 盒個數。

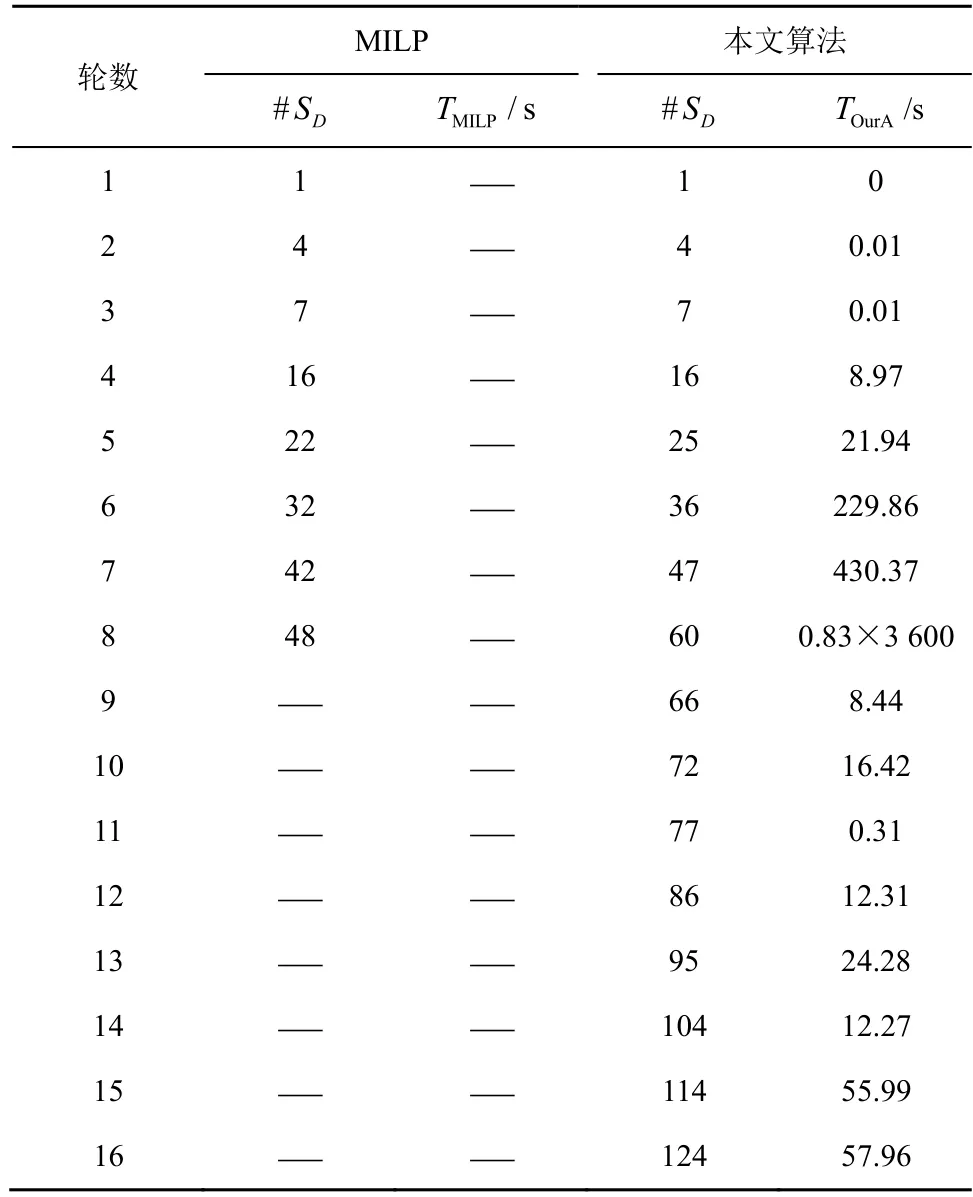
表4 FIDES 最小活躍S 盒個數

4 結束語

本文研究了分組密碼常用的MDS 矩陣和二元域矩陣的差分和掩碼傳播性質，提出了差分模式分布表和掩碼模式分布表的概念，證明了構造差分/掩碼模式分布表的計算復雜度的下界，并給出了快速構造方法。基于Matsui 算法，提出了一種自動化搜索SPN 型分組密碼最小活躍S 盒個數的快速算法，通過引入一些優化策略，極大提高了Matsui算法的效率。針對SPN 型分組密碼LED、SKINNY、CRAFT 以及認證加密算法FIDES，給出了其全輪最小活躍S 盒個數。實驗結果表明，本文算法的效率比基于MILP 的方法高。