考慮二元Copula統計量的晶圓制造疊加誤差監測

郝瀾宇 周 笛 李艷婷 潘爾順

上海交通大學機械與動力工程學院，上海，200240

0 引言

半導體技術一直是現代電子工業發展的原動力和重要基礎[1]，其應用領域包括新能源、信息通信設備、智能電網等。大多數用于微電子和光電子器件的集成電路是在其表面使用半導體晶片制造而成的[2]。晶圓是集成電路的主要原材料，其缺陷是影響產品合格率的主要因素[3]。晶圓制造過程復雜、漫長且成本高昂，必須在潔凈室環境中進行數個化學步驟，例如沉積、刻蝕、光刻等，并且需要監控大量關鍵過程。在制造過程中收集傳感器讀數和晶片形狀測量值等對工藝進行建模和監控[4]，及時準確地檢測缺陷，有助于質量控制，使產品達到更高的合格率。

晶圓數據具有高維特征，為后續的分析處理增加了難度。高維數據集應用越來越廣泛，為更好地解釋其含義，Pearson提出了主成分分析(principal component analysis, PCA)方法，既能以可解釋的方式降低數據維度，也能保留數據集的大部分統計信息[5]。盡管PCA方法在工程、生物學、社會科學等領域都有著廣泛的應用[6]，但仍存在部分缺點。首先，對于高維數據，PCA方法計算量較大，同時因其不能產生稀疏主成分而很難給出合理解釋；其次，PCA方法不穩定，魯棒性較差，對異常值非常敏感[7]。為此，MARONNA等[8]提出了一種最小二乘法PCA(least trimmed squares PCA, LTS-PCA)模型以增加穩定性；SHEN等[9]提出了一種基于正則化奇異值分解的稀疏PCA(sparse PCA via regularized singular value decomposition, sPCA-rSVD)模型，通過獲取稀疏主成分的方式來增強數據集的可解釋性，但穩定性較差。最終，為同時解決穩定性和可解釋性，WANG等[7]將LTS-PCA與sPCA-rSVD兩種方法相結合，提出了一種基于最小二乘法的稀疏PCA方法(LTS-SPCA)，計算更快速，模型更穩健，可解釋性更強，但該方法在處理某些高維數據集時不夠稀疏，導致模型復雜度偏高。

針對制造過程高維數據的異常監測，目前應用最廣泛的是多元統計控制圖方法[10]。考慮不同工程背景，現有大多數方法存在一定局限性。首先，缺少足夠的先驗理由，近似分布假設并不成立；其次，不同數據維度之間存在一定的相關性[11]，大多數多變量監測過程并不獨立[12]；然后，變量之間依賴結構不靈活，不利于對數據的靈活建模；最后，多元統計過程往往缺少確定的聯合分布來描述[13]。故將Copula模型引入多元統計控制圖，其原理主要是將單變量的邊緣分布函數和Copula函數進行組合，生成高維數據的聯合分布函數，可用于構建靈活準確的多元分布[14]，其中，Copula函數的選擇取決于變量間的相關關系。FATAHI等[15]提出了一種基于Copula函數的雙變量零膨脹泊松分布模型，基于所得的聯合分布建立了用于監控稀有事件的雙變量控制圖。VERDIER[16]提出了一種基于非參數核密度估計方法的多元Copula控制圖，由于Copula函數具有多種不同的分布族，適用于不同場景，故可以得到相對靈活的控制圖，并證明在監測非高斯分布數據時，經典Hotelling T2規則可能產生許多誤報。但通過密度估計方法構建Copula控制圖仍存在一定局限性，如可能無法檢測到受監控過程變量的多元分布形狀變化，如果密度估計錯誤則會導致大批量誤報等。KRUPSKII等[17]提出了兩種新的基于Copula性質的多變量監測方法，對分布變化更敏感，并且不需要估計聯合分布。

在晶圓制造中，數據維度高且耦合性強，其缺陷模式識別主要靠人工進行，現有大多數方法限于圖像分類，無法分析缺陷的根本原因，且圖像尺寸會影響到檢索性能，故將機器學習技術引入晶圓缺陷模式識別可大大提高識別能力[18]。CHIEN等[19]開發了一種集成空間統計和神經網絡的制造智能解決方案，用于晶圓地圖模式的檢測和分類，以構建一個在線監控和可視化系統，具有擴展的統計過程控制圖。WU等[20]利用SVM對晶圓缺陷模式進行分類，并通過歐氏距離和二維歸一化相關系數計算相似度，從而實現缺陷根源分析。YU等[21]提出了一種基于流形學習算法與高斯混合模型動態集成的晶圓缺陷模式識別方法。目前，基于離散數據的晶圓圖缺陷模式識別在很多研究中都很常見，但針對后續光刻步驟中檢測到的晶片重疊誤差連續數據卻少有人研究，具有挑戰性和必要性。

本文結合晶圓結構中的置換特征和反射特征，開展芯片制造過程中的缺陷誤差研究。針對高維連續晶圓數據難以準確監控的問題，本文在數據監測過程中充分考慮數據的可解釋性，改進LTS-SPCA降維模型，提出靈活度較高的穩健稀疏主成分分析技術，然后建立一種基于Copula的多元耦合統計量異常監測方法。

1 晶圓制造疊加誤差監測

晶片層與層之間的許多加工步驟都會引起整個晶圓的應力變化、扭曲或者形變，從而產生疊加誤差。疊加誤差可以體現所有過程中累積的應力變化[22]。圖1展示了一個簡化的晶圓疊加誤差產生過程。首先，在晶圓上進行沉積工藝并快速暴露在熱退火中[4]，使自由狀態的晶圓出現曲率。然后，將晶圓夾平，并在光刻工藝中進行圖案化。為了生成第二層圖案，需要改變晶圓的形狀再沉積一個新層。最后，平整的晶圓被圖案化。由于晶圓再次被壓扁，第一層圖案的距離增加，但新圖案的印刷距離L保持不變，導致圖案之間產生一定的錯位，即疊加誤差。

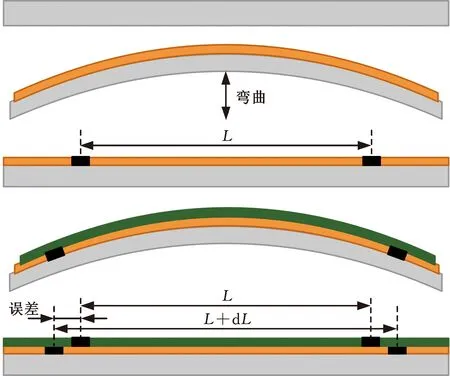
圖1 晶圓片誤差疊加過程[4]

數據集中包含大量正常情況和異常情況下的晶圓圖像，以此為基礎開展相關研究。其中，異常情況共有三種：X軸方向偏移、Y軸方向偏移和XY雙軸方向偏移。圖2是晶圓形狀和其對應的在X軸方向上發生偏移的疊加誤差異常圖像。

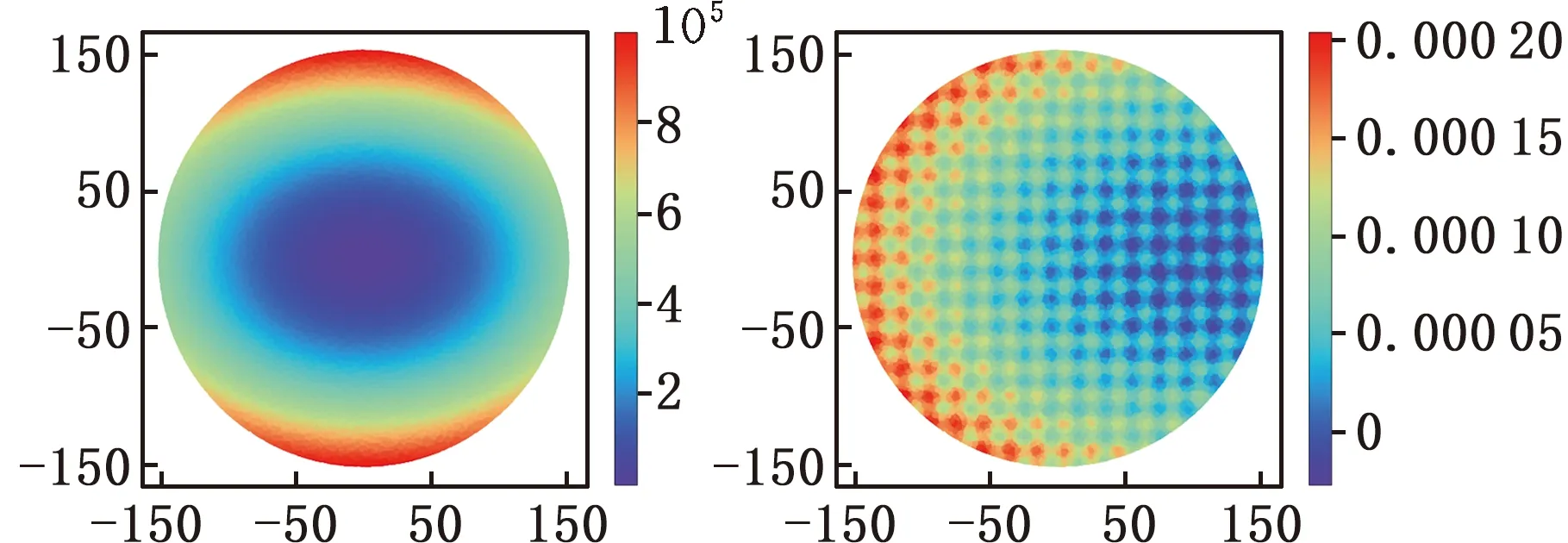
(a)晶圓形狀(b)X軸方向疊加誤差圖像

晶圓異常圖像主要由晶圓形狀及其對應的疊加誤差兩部分組成，且晶圓形狀會直接影響產生的疊加誤差。考慮幾種跨越不同空間波長范圍的晶圓形狀特征，確定晶圓的整體形狀在幾十微米的范圍內彎曲。只考慮弓形結構和微觀形貌，并假設在晶圓表面上沉積一層薄層，會導致晶圓形成弓形幾何形狀，公式如下：

(1)

式中，b1為弓形大小，設為100 μm；R為晶圓半徑，設為150 mm。

然后進行光刻工藝，晶圓形狀會發生弓形和波浪形變化：

(2)

式中，b2為弓形大小，通常在30～100 μm間均勻采樣；hi、λi為對應的波高和波長；p為假定的波形數量[4]。

引入平面內變形(in-plane distortion, IPD)的計算公式：

(3)

其中，ω表示加工工藝前的晶圓幾何形狀。由此可見，IPD與晶圓形狀的導數成一定比例。經過證明，可得

(4)

式中，ξ為常數，值為2/3；h為晶圓的厚度。

對于晶圓中的兩層晶片i和j，分別計算Dip并相減，則可以得到形狀-斜率差(shape-slope difference, SSD)，即Dss=Dip，i-Dip，j。根據模型對SSD進行修正，可得形狀-斜率殘差(shape-slope residual, SSR)rss，進而得到平面內預測變形殘差(predicted in-plane distortion residual, PIR)rpi的表達式：

rpi=c×rss

(5)

式中，c為一個常數，取決于晶圓厚度，通常取h/6[22]。

晶圓疊加誤差主要是指制造過程中平面變形引起的圖案錯位，受晶圓形狀、Dip和rss等多種因素影響。考慮到晶圓圖像的基本結構是圓形，對應坐標軸方向，存在置換特征和反射特征。正常圖像滿足置換對稱和反射對稱的性質，而平面變形后的異常圖像不滿足。根據其異常形式的不同，共分為X軸方向偏移、Y軸方向偏移和XY雙軸方向偏移三種誤差表現形式。

本文研究過程的流程如圖3所示。

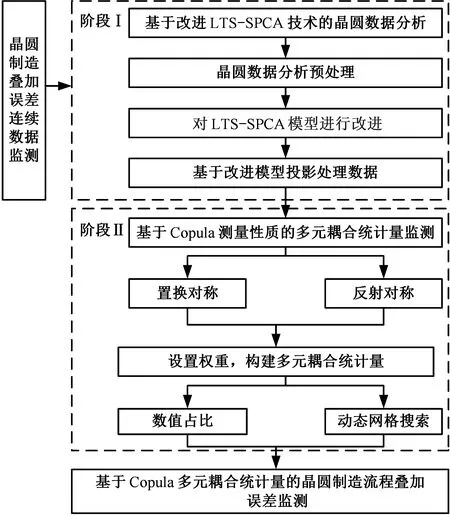
圖3 研究過程流程圖

2 基于改進LTS-SPCA技術的高維晶圓數據分析

2.1 晶圓數據分區預處理

從晶圓數據集中挑選1000張正常圖像、1000張X軸方向偏移異常圖像、1000張Y軸方向偏移異常圖像和1000張X、Y雙軸方向偏移異常圖像，共4000組數據用于研究。

因晶圓圖像中所包含的數據是高維且連續的，為脫離圖像本身，將晶圓圖像處理成只含有數據但不包含圖形信息的數據，使圖像尺寸不會對性能造成影響，因此需對圖像進行分區處理。將整個晶圓地圖按照圖4劃分為100個區域，可以看出，四角中共有12個區域會采集到無效數據，故將其剔除，得到88維有效數據。同時對數據進行去均值等處理后，可得到有效算例數據。

圖4 圖像分區示意圖

圖5是15個算例數據的前30個維度分布圖，可以看出不同維度數據間存在較大差異性。晶圓圖像中不同維度產生的疊加誤差不同，規律性不強，差異性較大。為提高監測算法精度，適當減小計算量，對高維晶圓分區數據進行異常監測時需進行一定的預處理。

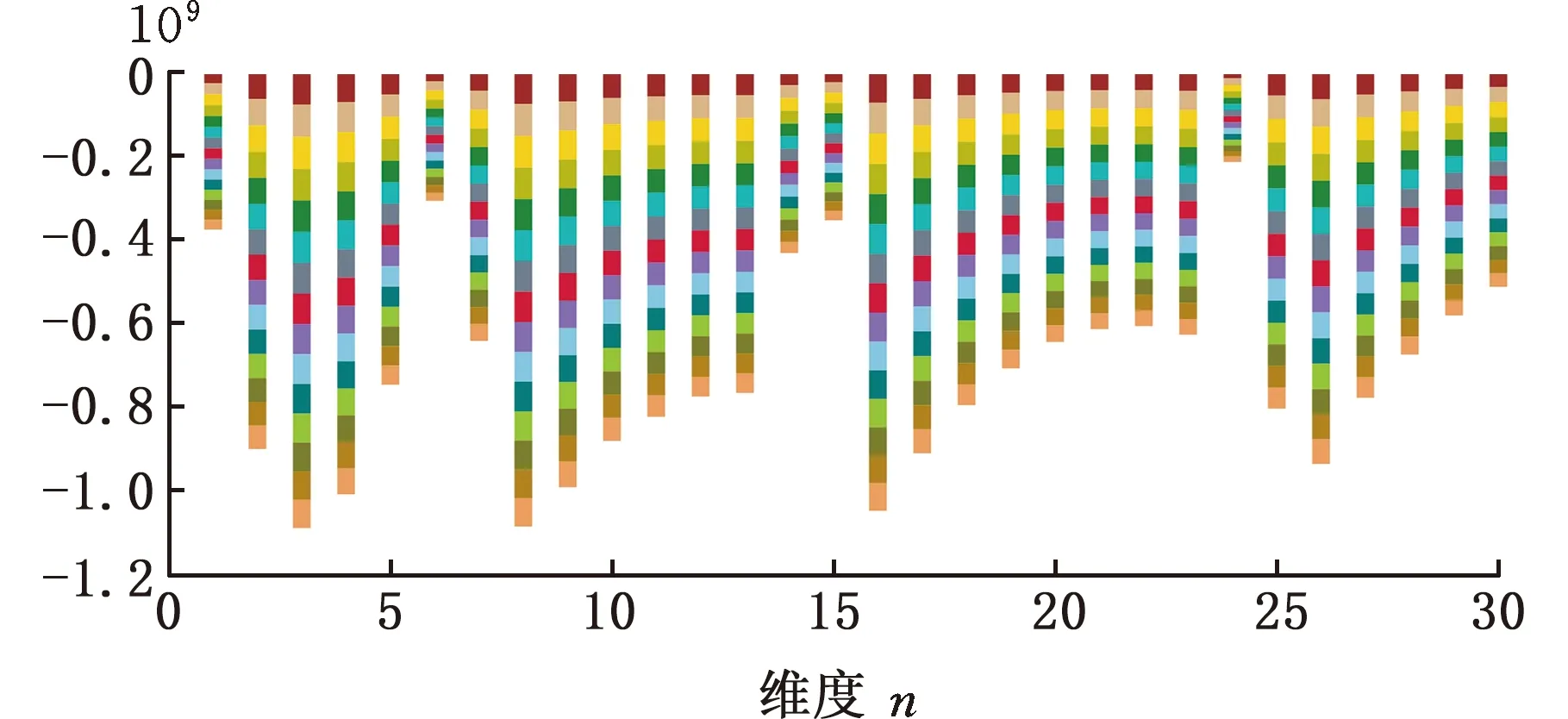
圖5 算例數據分布圖

考慮晶圓分區數據的維度差異性，對其進行簡單統計及可視化處理。圖6和圖7分別是正常晶圓數據和X軸方向偏移異常晶圓數據所對應的箱線圖，圖8是兩類圖像的中位數圖。由圖6和圖7可以看出，正常晶圓數據的分布相比異常數據更為分散。以圖2b所示晶圓X軸方向疊加誤差圖像為例，發現異常圖像因應力變化產生的變形會導致各維度的采集數據變小，符合數據分布規律。對比后可知，正常數據和異常數據的分布存在較為明顯的差異，具有一定區分性。

圖6 正常晶圓數據箱線圖

圖7 X軸方向偏移異常晶圓數據箱線圖

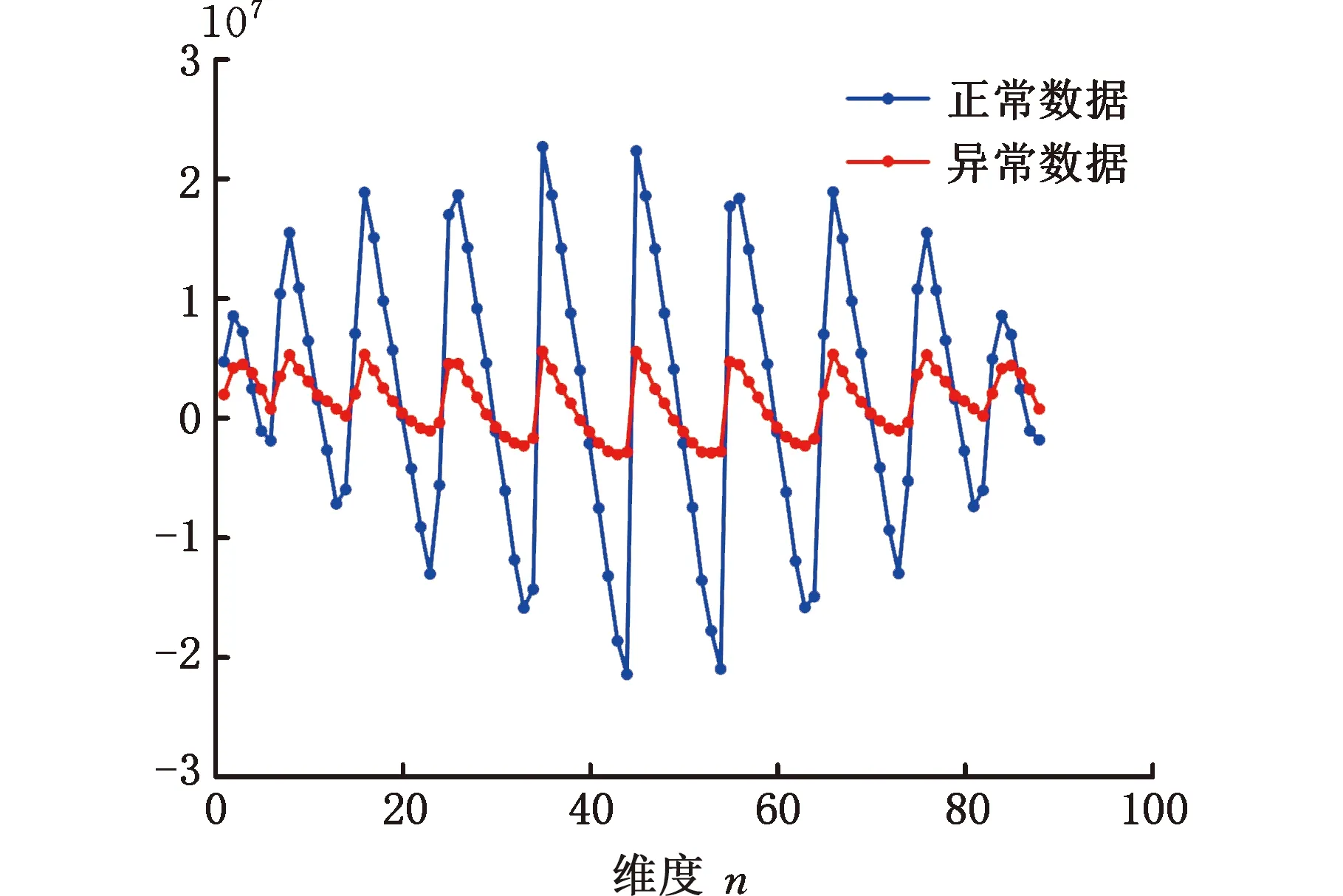
圖8 算例數據中位數圖

由圖8可以看出，維度8、維度16、維度25、維度26等在兩組數據中差異較大，能較好地判別數據是否偏移，而維度11、維度20、維度30和維度60等在兩組數據中幾乎具有相同的數值，對區分數據貢獻不大。不同維度數據所包含的價值不同，故對算例數據進行整合降維處理是有必要的。由此，結合所構建的晶圓圖像分區數據，展開高效的統計監測技術研究。

2.2 改進LTS-SPCA模型

考慮晶圓數據模型xi=μ+ρuiν+σzi，其中xi∈Rp(i=1,2,…,n)，μ∈Rp是xi的中心，ui～N(0,1)是獨立同分布的高斯隨機效應，ν∈Rp且‖ν‖2=1是要估計的單個主成分，同時，zi～N(0,Ip)是獨立的隨機噪聲向量。

(6)

(7)

(8)

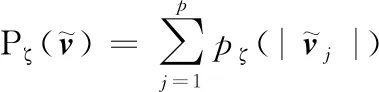
為增加穩定性，提出LTS-PCA模型[8]，其目標函數可以表示為

(9)

U=(u1,u2,…,un)T∈Rn×k

V=(v1,v2,…,vk)∈Rp×k

式中，(·)h為子矩陣。

將問題(8)和(9)相結合，則可以估計出稀疏且穩健的主成分，得到LTS-SPCA模型[7]，目標函數如下：

(10)

針對晶圓數據特性，在使用LTS-SPCA模型進行降維的過程中對其進行改進。在目標函數中加入新的懲罰項，在保證稀疏性的同時，限制各主成分中的各項系數不能過低，使其具有一定的物理意義。改進后的目標函數如下：

(11)

2.3 數據投影處理

晶圓數據集中共包含可用數據4000組，其中每類數據1000組。以識別X軸方向偏移異常為例，從正常數據和X軸方向偏移異常數據中各抽取600組作為訓練集，各剩余400組用來測試模型效果。利用改進LTS-SPCA模型對晶圓數據進行投影處理，得到效果最好的2個稀疏主成分。圖9為其對應的解釋方差圖，可以看出，前2個主成分數值偏大，整體占比較高，能更好地刻畫晶圓特征。

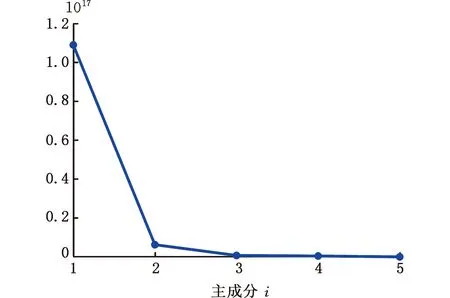
圖9 解釋方差圖

圖10是2個稀疏主成分所對應的各維度系數分布圖。結合圖像分區原則，對主成分所提取的區域進行標注，結果如圖11所示。由圖11a可以看出，第一主成分的系數較為分散，除維度44外，其余系數呈上下對稱分布，分別對應圖10中紅色虛線凸起部分。由圖11b可以看出，第二主成分的系數主要分布在4個維度，呈上下對稱分布，分別對應圖10中藍色虛線凸起部分。

圖10 各維度系數分布圖

(a)第一主成分標注圖 (b)第二主成分標注圖

根據改進LTS-SPCA模型的計算結果對晶圓分區數據進行投影處理，篩選出有效數據。此時，88維數據被處理為2維投影數據，保留了絕大部分統計信息的同時還提高了數據的可解釋性。利用改進方法實現數據降維技術，可通過較小的數據量監測出連續數據的變化，效率更高。

3 基于Copula性質的統計量監測方法

3.1 Copula性質

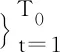
(12)

設c0為對應于密度f0的Copula分布，并令晶圓數據變量(U1,U2,…,Um)T的密度為c0。定義統計量ξk如下：

(13)

對于偶數k，統計量ξk可以檢測整體依賴性強度的變化；而對于奇數k，則可以用來測量偏度變化。其對應的經驗估計為

(14)

ξ2也可以看作皮爾遜相關系數的多元形式，公式如下：

(15)

其中，ρi1,i2=cor(Ui1,Ui2)是皮爾遜相關系數。不同維度數據間的皮爾遜相關系數越大，說明ξ2統計量的值越大。根據晶圓圖像的結構特征，考慮對其置換對稱性和反射對稱性進行監測。圖12所示是同一晶圓異常圖像的置換和反射特征。置換對稱性可以通過整體依賴性來測量。如圖12a所示，以X軸方向偏移的晶圓異常圖像為例，可得到其置換圖像(圖12b)，說明統計量ξ2主要監測與坐標軸成45°角方向的數據變化。偏度是反射對稱性質的一種體現[23]。如圖12c所示，同樣可以得到其反射圖像，說明統計量ξ2k+1主要監測坐標軸方向的數據變化趨勢。

(a)晶圓異常圖像 (b)置換圖像

3.2 晶圓制造疊加誤差的監測結果

經過證明，當數據維度小于10時，統計量ξ7對函數反射對稱性的變化最為敏感，故設參數k為3[23]。計算可得統計量ξ2的值為0.2480，所對應的置信區間為(0.2432，0.2528)，異常數據監測準確率為83.95%；統計量ξ7的值為-0.0076，所對應的置信區間為(-0.0079，-0.0073)，異常數據監測準確率為89.97%。圖13和圖14分別從不同角度展示了部分數據的監測結果及過程。圖13共包含兩個控制圖，分別對應統計量ξ2和統計量ξ7的部分異常數據監測結果。在測試數據集中，存在部分數據未被統計量ξ2判定為異常但統計量ξ7監測出了其異常狀態，例如數據點16等，同時仍存在部分數據未被統計量ξ7判定為異常但統計量ξ2監測出其異常狀態，例如數據點5等。由此可得，同時監測基于置換對稱和反射對稱的兩個統計量可有效提高異常數據的監測效果，在一定程度上互為補充。如圖14所示，考慮到兩個統計量數量級差距過大，需構建一種新的多元耦合統計量來更直接有效地監測數據異常。

(a)統計量ξ2

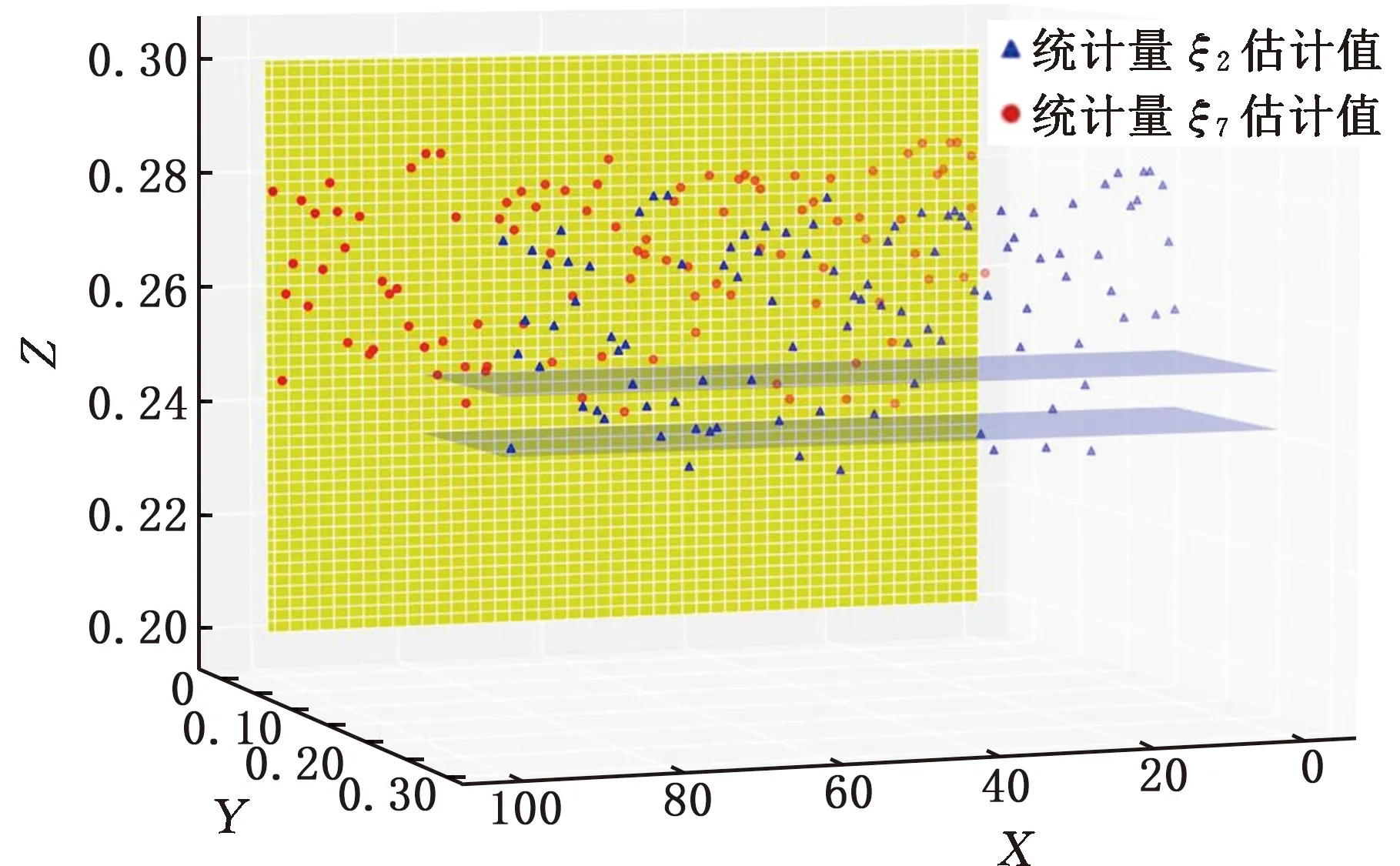
圖14 監測結果三維圖像

4 多元耦合統計量異常監測方法

為更好地結合置換對稱和反射對稱兩種性質，需設置不同的權重值來構建一種準確有效的多元耦合統計量。權重的設置是否合理會直接影響其監測效果，因此，使用多種算法來計算統計量ξ2、ξ7對應的權重值ω2和ω7。考慮到其對應的數量級不同，可以通過數值占比方式確定權重，公式如下：

(16)

通過計算可以求出ω2的值為0.0306，ω7的值為0.9995，從而得到新的置信區間為(-0.0005，0.0004)。利用耦合統計量ξm監測異常數據集，可得準確率為90.64%。

同時考慮使用最優算法來計算統計量的權重，為消除數據間的量級差異，對其進行歸一化處理。結合晶圓異常圖像的結構特征可知，制造過程產生的疊加誤差越大，其對應的統計量估計值越偏離正常經驗統計量值，故兩者之間的距離可作為評判標準。針對同一異常圖像，與經驗統計量值的距離越大說明耦合統計量的設計越有效。因此，最優算法的目標函數設為不同訓練數據的多元耦合統計量ξn估計值與經驗統計量值的距離平方和，同時為方便理解，約束條件中將權重之和定為1。具體問題描述如下：

(17)

s.t.ω2+ω7=1 0<ω2<1 0<ω7<1

根據動態網格搜索算法求解，當訓練數據集不同時，問題(17)對應不同的最優解結果如圖15所示。由圖15可以看出，隨著訓練數據集逐漸增大，異常監測的準確率呈波動趨勢，而問題(17)的最優解逐漸收斂。根據ω2和ω7的收斂趨勢，當ω2取0.3527、ω7取0.6473時，問題(17)得到最優解。此時，耦合統計量ξn的表達式為ξn=0.3527ξ2+0.6473ξ7。基于上文構建的晶圓異常模擬數據集，結合改進的LTS-SPCA降維模型對其進行投影處理，并利用多元耦合統計量ξn進行異常監測。異常數據共1200組，其中包括400組X軸方向偏移異常數據、400組Y軸方向偏移異常數據和400組XY雙軸方向偏移異常數據。根據控制圖建立流程，統計量ξn對應的置信區間為(0.0807，0.0844)，監測異常數據的準確率分別為91.50%、91.25%和92.50%。圖16所示為三類異常數據對應的混淆矩陣。可以看出，XY雙軸方向偏移異常的監測準確率略高于其他兩種偏移異常的監測準確率。通過對異常數據集進行監測可得，統計量ξn的平均準確率為91.75%。

圖15 動態網格搜索求解結果

(a)X軸方向偏移異常數據 (b)Y軸方向偏移異常數據

用于比較的監測方法包括多元耦合統計量ξm控制圖、多元耦合統計量ξn控制圖、基于置換對稱的統計量ξ2控制圖、基于反射對稱的統計量ξ2k+1控制圖、LTS-SPCA控制圖、SPCA-Copula控制圖和Copula控制圖，比較結果見表1。由表1可以看出，所提出的多元耦合統計量控制圖的監測效果明顯優于其他幾種方法。多元耦合統計量ξm和ξn異常監測準確率均超過90%，其中統計量ξn準確率最高，達到91.75%，實驗結果證明所提方法能較準確地監測出晶圓數據異常。

表1 模型比較結果

考慮晶圓制造過程中可能出現的加工誤差、測量誤差和人為誤差等情況，本文在晶圓疊加誤差數據模型中加入隨機噪聲擾動。針對X軸方向偏移、Y軸方向偏移和XY雙軸方向偏移三種異常情況，各模擬出400組誤差數據用于實驗驗證，發現新方法的平均異常監測準確率仍能達到90.58%。當噪聲強度服從N(0,4)分布時，無噪聲和有噪聲兩種情況下的部分異常數據監測結果如圖17所示。由此可見，所提方法在無噪聲和有噪聲兩種情況下都具有穩定的效果，能對晶圓制造過程中的疊加誤差異常進行及時的監測預警，具有一定的普適性。

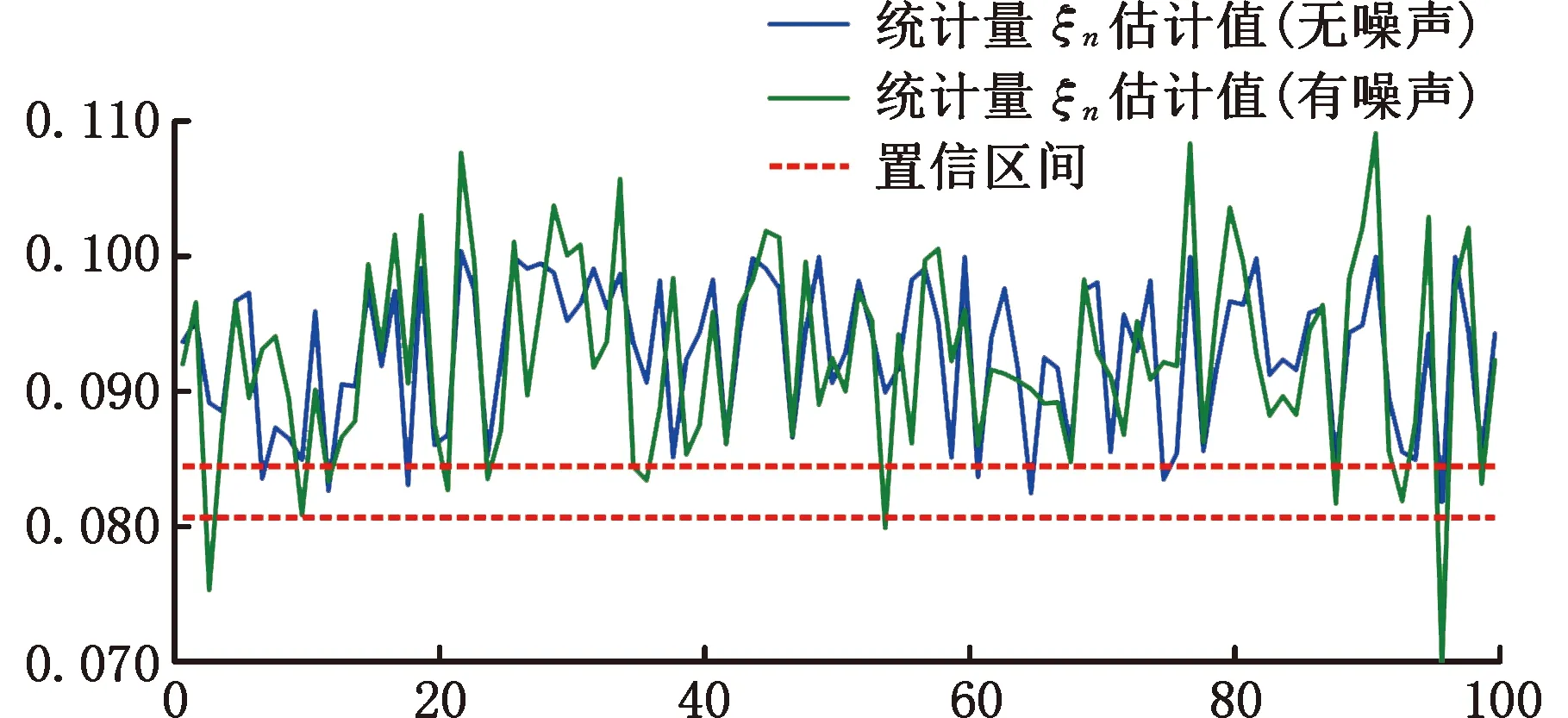
圖17 部分異常數據監測控制圖

5 結語

結果顯示，所提方法監測異常數據的準確率可達91.75%，說明所提方法既可靈活有效地處理高維連續數據，又能有效結合Copula統計量準確監測制造誤差，具有較高的工程應用價值。后續仍需進一步結合晶圓監測數據，豐富不同工況下數據集樣本量，開展基于多元耦合統計量的晶圓制造誤差高效監測技術研究。