基于RBF的隧洞巖體蠕變參數反演方法

李志剛，王忠全，張云山，徐 潔，楊 帆，黃 銘

(1.中國水利水電第一工程局有限公司，長春 130033；2.合肥工業大學 土木與水利工程學院，合肥 230009)

0 引 言

近年來，為解決部分地區干旱缺水問題，水資源調配工程不斷發展，隧洞穿越地層的地質條件也越發復雜，時常會遇到斷裂、破碎、軟巖等不良地質情況，對隧洞施工期和運行期安全造成威脅[1]。由于軟巖的流變特性，在軟巖地層開挖隧洞過程中，洞周圍巖變形并不僅僅是瞬時完成的彈性變形，還有隨著時間不斷增長的蠕變變形，從而導致隧洞結構產生變形和破壞[2-3]。為了掌握隧洞開挖變形規律，準確預測洞周圍巖蠕變變形，需要建立準確合理的數值模型。數值模型中，巖體的力學參數必不可少，而蠕變參數又是其重要組成部分[4]。

由于尺寸效應和工程因素的影響，通過現場或室內蠕變試驗所獲得的巖體力學參數往往不能反映現場大范圍圍巖的綜合性質。因此，如何獲取較為準確的蠕變參數成為制約巖體工程理論分析和數值計算的關鍵問題[5-6]。20世紀70年代以來，迅速發展的反演方法為解決這一問題提供了有效手段。近年來，國內外學者在參數反演方面進行了大量的研究工作[7-8]。Atsushi S等[9]采用能反映蠕變第三階段的本構模型對隧道參數進行了研究，提供了隧道失穩對策；劉杰等[10]改進遺傳算法，并應用于黏彈性本構模型上，利用普通遺傳算法得到的優秀個體逐步優化搜索區間，提高運行效率。

雖然針對蠕變參數反演的研究成果較多，但對于實際工程來說，不同類型的圍巖性質之間存在較大差異，蠕變參數與位移值之間關系復雜。RBF神經網絡結構清晰，學習收斂速度快，且具有較好的全局逼近能力。因此，本文提出一種基于徑向基函數(RBF)和FLAC3D仿真計算的隧洞巖體蠕變參數反演方法，并將該方法應用于滇中引水工程中。結合現場監測資料，采用與位移規律相符的本構模型，建立反映隧洞開挖支護工序以及長期蠕變過程的三維仿真計算模型。利用敏感性分析方法確定待反演參數。采用RBF神經網絡聯合仿真模型進行反演計算。研究成果為指導此類隧洞工程快速獲取巖體蠕變參數，對隧洞開挖支護進行仿真計算，掌握隧洞開挖及長期洞周位移時空變化規律提供參考。

1 蠕變本構模型及參數反演方法

1.1 Burgers模型

巖體的蠕變過程十分復雜，構建合理有效的巖體蠕變本構模型，是開展參數反演并實現能夠揭示合理變形規律的隧洞開挖數值仿真的前提。根據相關工程資料顯示，本文分析的巖體埋深較大且地應力偏高，巖體流變效應明顯，其巖體變形特征與伯格斯模型(Burgers)較為符合。

Burgers模型是一種四參數黏彈性模型，由Maxwell體和Kelvin體串聯而成，能夠反映巖體瞬時變形、衰減蠕變和等速蠕變階段[11]。根據Burgers模型組成特點，基于連續介質理論可以求出模型的蠕變方程為：

(1)

式中：ε為應變；σ為應力，Pa；EM、ηM分別為Maxwell彈性模量、黏滯系數，EK、ηK分別為Kelvin黏彈性模量、黏滯系數，GPa、GPa·s。

本次數值仿真中，采用Burgers模型，該模型可以把復雜的蠕變過程直觀地表達出來，能夠反映洞周巖體的黏彈性蠕變特征。

1.2 RBF神經網絡

軟巖隧洞圍巖力學參數復雜，為準確描述巖體變形與參數之間的非線性關系，采用具有超強非線性映射能力的神經網絡。RBF神經網絡即徑向基函數(Radial Basic Function)神經網絡，是一種前饋神經網絡，因其結構清晰，學習收斂速度快，且能夠逼近任意非線性函數而受到廣泛應用[12]。因而，本文采用RBF神經網絡對蠕變參數進行參數反演研究。

RBF神經網絡由輸入層、隱層、輸出層3層結構組成。同層神經元之間沒有聯系，信號僅從上層神經元向下層傳輸，即輸入層神經元只傳遞輸入信號至隱層。

隱層神經元中的作用函數即基函數，對輸入信號將在局部產生響應。最常用的基函數是高斯函數：

(2)

式中：X為n維輸入向量；Ci為第i個基函數的中心(與X具有相同的維度)；σi為第i個變量，它決定該基函數圍繞中心點的寬度；B為隱單元的數量；‖X-Ci‖為X與Ci之間的距離。

由式(2)可知，輸入與中心的距離越遠，節點的響應就越大。在RBF神經網絡中，從輸入層到隱層的變換是非線性的，隱層把輸入向量從低維空間映射到高維空間，從而實現線性運算，網絡輸出為隱層神經元輸出的線性加權和，即：

(3)

式中：ωij為隱層神經元與輸出之間的連接權；M為輸出維數。

1.3 基于RBF的蠕變參數反演流程

本文將建立基于RBF神經網絡的巖體蠕變參數反演方法，該方法基本計算流程見圖1。

圖1 基于RBF神經網絡的巖體蠕變參數反演計算流程

具體計算步驟如下：①根據工程現場監測資料和工程地質報告，并類比其他同類工程相關經驗，綜合分析選定合適的巖體蠕變本構模型。②采用敏感性分析方法，確定待反演巖體力學參數及其取值范圍。③采用正交試驗設計法，建立不同參數多水平的試驗組合。④基于Flac3D建立的三維隧洞開挖蠕變數值計算模型，獲取不同參數組合的圍巖位移值并記錄，構造RBF神經網絡學習樣本。⑤將樣本代入RBF神經網絡中進行訓練，建立待反演參數與圍巖位移之間的非線性映射關系。⑥將實測位移值輸入到已經訓練好的RBF神經網絡中，反演得到相關蠕變參數取值。⑦將反演得到的蠕變參數代入數值計算模型中，得到不同測點的計算位移值，計算出測點實測值與計算值之間的誤差，對反演結果進行檢驗和評價。

2 工程實例

滇中引水工程具有隧洞線路長、穿越地質條件復雜等特點。本文分析實例中的隧洞位于滇中引水工程楚雄段，隧洞全長4 755m，隧洞埋深一般在150～200m，最大埋深252m。隧洞穿越地層除隧洞進出口有第四系覆蓋層之外，前段以滇中紅層中的侏羅系、白堊系沉積巖地層為主，后段以昆陽群變質巖地層為主，且隧洞穿越軟巖及較軟巖的洞段占全長的48.7%。滇中紅層軟巖具有流變效應，對穿越滇中紅層建筑物的長期穩定性具有較大影響。

2.1 數值計算模型

根據該隧洞工程地質情況和監測斷面布置情況，選取隧洞前段建立三維數值計算模型。該洞段為IV類圍巖，隧洞斷面尺寸為9.86m×10.56m(寬×高)，斷面形狀為馬蹄形，隧洞尺寸及監測點布置情況圖2。

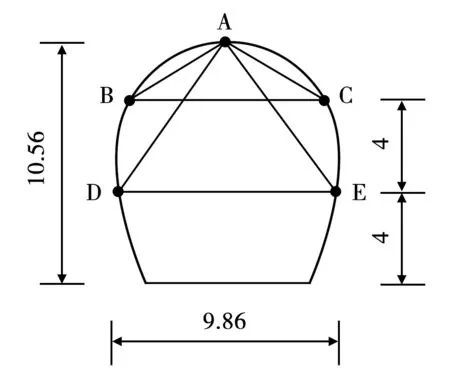
圖2 隧洞斷面監測點布置情況

根據圣維南原理，模型范圍取5倍洞徑，即左右及下部邊界取距隧洞斷面軸線50m，隧洞頂部取至地表面，洞長沿洞軸線方向取100m。由于隧洞穿越段風化層距隧洞較遠，且該洞段巖性一致，故本文中采用同一巖層進行模擬。利用Ansys建立模型之后，導入Flac3D進行數值計算，模型見圖3。圍巖采用實體單元進行模擬，錨桿支護采用cable結構單元模擬，鋼支撐采用beam結構單元模擬，鋼拱架作用等效折算至混凝土噴層，噴層采用shell結構單元模擬。共劃分單元80 445個。

圖3 隧洞三維數值計算模型

模型四周和底部邊界均采用法向約束，頂面為自由邊界。隧洞開挖采用上下臺階法，循環進尺2m，上下臺階共計100個開挖步，每次開挖后進行錨固支護，支護落后于掌子面0.5m，開挖完成后，再進行共計150天的蠕變計算。

2.2 蠕變參數反演

2.2.1 敏感性分析

在進行圍巖蠕變參數反演計算時，首先要確定待反演參數。由于圍巖力學參數數量較多，為了提高參數反演結果的質量及精度，更準確揭示洞周圍巖變形規律，可根據“敏感性原則”，選取對圍巖長期變形影響較大的參數作為待反演參數。

本文主要對圍巖基本力學參數進行敏感性分析，以隧洞拱頂以及左右拱肩沉降位移值作為參數敏感性大小的判別依據，利用極差法進行分析。首先采用正交試驗設計法對彈性模量、泊松比、黏聚力、內摩擦角建立L9(33)正交表，利用2.1一節所建立的數值模型計算得到各測點位移值。在此基礎上，采用極差法進行分析并得到結果，以拱頂為例，各參數對拱頂沉降值的影響見圖4。

圖4 各參數對拱頂沉降值的影響圖

由圖4可知，對圍巖變形影響最大的是彈性模量E，黏聚力和內摩擦角次之，最弱的是泊松比。當保持彈性模量E不變，黏聚力從0.25MPa增大至0.45MPa時，拱頂沉降值變幅為0.4mm；內摩擦角從22°增大至32°時，拱頂沉降值變幅為0.3mm，與彈性模量對變形的影響相比可以忽略。所以，本文選取彈性模量E作為待反演參數。

由于本文研究的紅層軟巖在隧洞開挖時的變形具有明顯的蠕變特征，Burgers模型的4個參數分別控制彈性變形和黏滯流動變形，其值均對位移有較大影響。為了更準確描述隧洞長期蠕變變形規律，Burgers模型的4個蠕變參數均作為待反演參數。

2.2.2 構造訓練樣本

根據敏感性分析結果，結合工程地勘資料，并類比滇中同類工程，綜合分析確定待反演參數取值范圍，見表1。

表1 待反演參數范圍

采用正交試驗設計方法，對每個參數取5個水平，共構造25組參數組合，代入Flac3D數值模型進行計算，得到各參數組合對應的拱頂及左右拱肩沉降計算值。將各測點位移值作為輸入值，5個待反演參數作為輸出值，構成RBF神經網絡的訓練樣本。

2.2.3 反演計算及結果驗證

根據工程現場監測資料，提取監測斷面拱頂以及左右拱肩沉降位移的穩定值作為輸入值，代入訓練好的RBF神經網絡中，得到相應的彈性模量和蠕變參數結果，見表2。

表2 參數反演結果

將反演得到的參數值代入數值模型中進行模擬計算，得到各監測斷面的測點沉降計算值。提取監測斷面的各測點沉降計算值，計算實測值與數值計算值之間的相對誤差。結果表明，計算值與實測值之間最大相對誤差僅為6.44%。

然后采用后驗差方法檢驗反演參數的準確性。D為數值計算值方差與實測值方差的比值，當D<0.35時，可以判斷反演精度為好。本文中D值為0.124 4，表明反演精度等級為好。

綜上所述，基于RBF神經網絡反演得到的蠕變參數計算所得沉降計算值與實測值之間誤差小，反演結果可靠，精度高。

3 結 論

采用基于RBF神經網絡的計算程序，對滇中紅層軟巖蠕變參數進行了反演分析，對比實測位移值與數值計算值之間的誤差，結論如下：

1)基于正交試驗設計和Flac3D數值計算進行敏感性分析，通過極差分析發現，影響圍巖位移值的巖體力學基本參數重要性依次為彈性模量、黏聚力、內摩擦角、泊松比。

2)采用RBF神經網絡和Flac3D數值計算模型，基于隧洞實測位移值進行參數反演，計算過程簡捷、快速。對比實測值與計算值之間的誤差，并進行后驗差分析，反演精度較高，是一種較好的反演分析方法，可以用于類似滇中紅層軟巖隧洞工程蠕變參數的確定。

3)三維模型更有利于掌握洞周圍巖時空變化規律。基于三維數值計算模型反演得到的蠕變參數，仿真模擬得到的隧洞開挖支護以及長期蠕變的位移、應力等情況，更符合工程實際，能夠準確揭示隧洞開挖應力、變形特征，可用于研究軟巖隧洞施工工法和支護參數及支護時機的確定。