精英反向黃金正弦海洋捕食者算法*
張 磊,劉 升,高文欣,郭雨鑫
(上海工程技術大學管理學院,上海 201620)
1 引言
海洋捕食者算法MPA(Marine Predators Algorithm)[1]是一種新穎的群智能算法。該算法已被成功地用于處理多級圖形分割[2]、預測新冠肺炎的病例數[3]、提高冷熱電聯產系統在環境、熱力學和經濟學方面的性能[4]等。
為了使海洋捕食者算法具有更加出色的性能,國外的部分研究人員對該算法進行了有效的改進。文獻[5]將海洋捕食者算法與教與學的優化算法相結合,避免了算法過早地收斂。文獻[6]將高質量解的位置通過自適應變異操作進行改進,而低質量解的位置則根據最優解的位置和從種群中選出的高質量解的位置進行更新,提升了算法的性能。
由于海洋捕食者算法提出的時間還不長,人們對其的認識和研究還不夠深入。本文針對其求解準確度低和穩定性差等特點,采用精英反向學習和黃金正弦來改進海洋捕食者算法,使得基本算法的魯棒性和計算精度得到提升。
2 海洋捕食者算法
2.1 初始化
MPA通過式(1)生成初始種群:
X0=Xmin+rand(Xmax-Xmin)
(1)
其中,Xmax和Xmin分別是解空間的上界和下界;rand是[0,1]的隨機數。
精英捕食者的矩陣表示E和獵物的矩陣表示P分別如式(2)和式(3)所示:
(2)
(3)
其中,N表示種群規模,D為種群中個體的維度。
2.2 探索階段
當迭代次數小于迭代總次數的三分之一時,算法處于探索階段,主要是為了探索搜索空間。在該階段中獵物的移動速度要比捕食者快,其數學模型如式(4)所示:
(4)
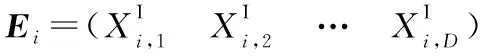
2.3 探索與開發之間的轉換
當迭代次數處于迭代總次數的前三分之一到三分之二時,算法處于探索與開發之間的轉換階段。在該階段中,捕食者的移動速度和獵物的相同,且前一半種群進行萊維飛行狀負責開發,后一半種群進行布朗運動負責探索,如式(5)~式(7)所示:
i=1,2,…,N/2,
(5)
i=N/2+1,…,N,
(6)
(7)
其中,RL表示由萊維分布生成的隨機向量;CF是自適應參數,用于調節捕食者運動的步長。
2.4 開發階段
當迭代次數處于迭代總次數的后三分之一時,捕食者使用Lévy策略進行開發,其數學模型如式(8)所示:
(8)
2.5 渦流形成和魚類聚集裝置的作用
魚類聚集裝置FAD(Fish Aggregating Device)等環境問題會對海洋捕食者造成影響,可看作是局部極值,采用如式(9)所示的數學模型消除部分影響:
(9)
其中,FFADs表示影響海洋捕食者減小局部極值影響的概率,取值為0.2;U是由0和1組成的向量;r是[0,1]的隨機數;Pr1和Pr2分別是從所有獵物矩陣中隨機選取的2個獵物。
3 融合精英反向黃金正弦的海洋捕食者算法
3.1 精英反向學習機制
反向學習機制OBL(Opposition-Based Learning)[7]的主要思想是同時計算并判斷候選解決方案和對應的反向解決方案,并通過其適應性值從中選擇最佳的候選解決方案。OBL策略能夠更有效地提高種群多樣性,并防止算法過早收斂。
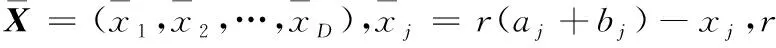
OBL可以更好地擴展種群的搜索范圍,提高算法性能。但是,OBL在生成其相反的解時具有一定的隨機性。相較于其相反的個體,每個隨機生成的候選者都有50%的概率遠離問題的最佳解。
精英反向學習EOBL(Elite Opposition-Based Learning)[8],以提高反向學習的求解質量為目的。EOBL的主要思想是通過評估精英解決方案的相反解決方案來產生更有希望的解決方案。相反的解決方案更有可能位于全局最優值所在的位置。這一機制已經成功應用于鯨魚算法[9]、正余弦算法[10]和哈里斯鷹算法[11]等的改進。

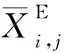
(10)

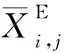
(11)
3.2 黃金正弦算法
黃金正弦算法GSA(Golden Sine Algorithm)[12]結合使用正弦函數與黃金分割系數來進行迭代搜索,具有優秀的尋優能力。
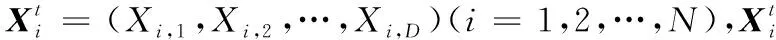
(12)
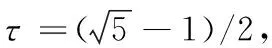
將黃金正弦算法融入到海洋捕食者算法中,按照式(13)更新海洋捕食者個體的位置:
Pi+1=Pi×|sin(R1)|+R2×sin(R1)×
|h1×Ei-h2×Pi|
(13)
其中,i=1,2,…,N/2;0≤it≤Max_iter。
綜上所述,融合精英反向學習和黃金正弦算法的海洋捕食者算法EGMPA(Elite opposition-based Golden-Sine Marine Predators Algorithm)的偽代碼如下所示:
EGMPA偽代碼
1.初始化種群;
2.While終止條件不滿足
3. 計算適應度,構造精英矩陣;
4. 生成反向種群OP={};
5. 根據lbj=min(Xi,j)和ubj=max(Xi,j), 計算個體的搜索邊界;
7. 從當前種群和OP種群中選擇適應值較好的個體作為新一代種群;
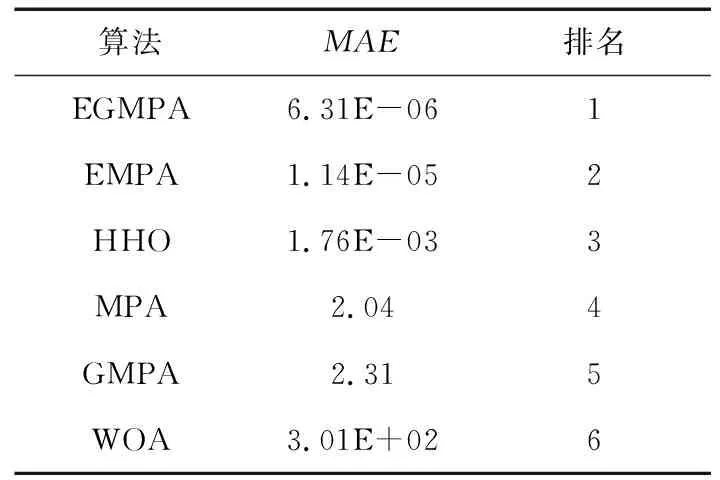
8.IfIter 9. 根據式(4)和式(13)更新獵物矩陣; 10.ElseifMax_Iter/3≤Iter<2*Max_Iter/3 11.對于前半部分種群(i=1,…,N/2), 根據式(5)和式(13)更新獵物矩陣; 12.對于后半部分種群(i=N/2,…,N), 根據式(6)和式(13)更新獵物矩陣; 13.ElseifIter≥2*Max_Iter/3 14.根據式(8)和式(13)更新獵物矩陣; 15.Endif 16. 完成精英矩陣的更新; 17. 應用FADs效果和基于式(9)進行更新; 18.Endwhile 海洋捕食者種群規模是N,搜索空間的維度是D,最大迭代次數是Max_iter,那么原始的海洋捕食者算法的時間復雜度是O(N×D×Max_iter)。EGMPA算法中,精英反向學習策略的時間復雜度是O(N×D),計算適應度值的時間復雜度是O(N×D),計算個體位置更新的時間復雜度是O(N×D),則EGMPA的時間復雜度為O(N×D×Max_iter)。EGMPA算法的時間復雜度與基本的MPA算法的相同,說明2種改進策略沒有增加海洋捕食者算法的計算負擔。 本文選取鯨魚優化算法WOA(Whale Optimization Algorithm)[13]、哈里斯鷹優化算法HHO(Harris Hawks Optimization)[14]、海洋捕食者算法MPA、僅引入精英反向學習的海洋捕食者算法EMPA(EOBL Marine Predators Algorithm)、僅引入黃金正弦的海洋捕食者算法GMPA(GSA Marine Predators Algorithm)與精英反向學習和黃金正弦的海洋捕食者算EGMPA進行比較。初始種群數量都設定為30,最大迭代次數都設定為500。 本文選取12個常用的基準測試函數對各算法進行性能測試,函數的相關屬性如表1所示。 Table 1 Test functions表1 測試函數 上述每種算法在每個基準測試函數上分別運行30次求平均值,實驗結果如表2所示。 Table 2 Test results表2 測試結果 從表2可以看到,對于12個測試函數,EGMPA在最優值、平均值和標準差的求解結果上比MPA、EMPA、GMPA、WOA和HHO都要好。對于測試函數f1,EGMPA可計算得到最優值0;對于測試函數f2~f4,EGMPA計算得到的最優值和平均值要比其他5種算法高出100多個數量級,標準差為0,魯棒性更好;對于測試函數f5,很難計算得到全局最優值,EGMPA計算的平均值比EMPA高出13個數量級,比HHO高出18個數量級,比MPA、GMPA和WOA高出22個數量級;對于測試函數f6和f7,EGMPA的尋優結果比其他5種算法都要好。對于函數f8~f12,EGMPA尋優的精度和魯棒性是最優的。上述表明精英反向學習和黃金正弦2種方法對MPA的優化效果是明顯的。 圖1展示了所用測試函數的收斂曲線,更清楚地表明了EGMPA的尋優效果。 Figure 1 Convergence curves圖1 收斂曲線圖 從圖1可知,改進的EGMPA收斂精度和收斂速度都要優于MPA、EMPA、GMPA、WOA和HHO,說明引入2種策略的EGMPA優于單一策略改進的海洋捕食者算法,具有優秀的尋優能力。 在對上述6種算法的計算能力的比較中,只采用最優值、平均值和標準差這3個指標來評價是不充分的,因此本文采用了Wilcoxon秩和檢驗來檢驗,結果如表3所示。當p<0.05時,說明2種算法的尋優效果有差異,反之則沒有。 Table 3 Test results of Wilcoxon rank sum 表3 Wilcoxon秩和檢驗結果 從表3可以看出,對于除了函數f7、f8、f9和f10外的所有函數,EGMPA與其他算法之間的p值都遠小于0.05,說明EGMPA具有更好的尋優性能;對于函數f7,EGMPA的尋優結果略優于GMPA的。表3中出現的NaN,表示相應算法都找到了全局最優值。 平均絕對誤差MAE(Mean Absolute Error)[15]表示結果與實際值之間差值的絕對值的平均值。MAE的數學定義如式(14)所示: (14) 其中,mi是每種算法在每個測試函數上計算得到最優解的平均值,ki是每個測試函數的理論最優值,n是測試函數的個數。MAE的數值越小,算法的計算性能越高。根據MAE值對各算法的排序結果如表4所示。 Table 4 Sort results by MAE 表4 MAE排序結果 從表4可知,EGMPA的MAE值最小,說明EGMPA的尋優性能更優。 IEEE CEC 2017測試集的具體信息見參考文獻[16]。不失一般性,本文在CEC 2017 基準函數中選取部分單峰、多峰、混合和復合類型的函數來驗證本文算法的性能。將精英反向學習黃金正弦的海洋捕食者算法EGMPA與基本的海洋捕食者算法MPA、基于教與學的海洋捕食者算法TLMPA(Teaching-Learning-based Marine Predators Algorithm)[3]、粒子群優化PSO(Particle Swarm Optimization)算法[17]、黃金正弦算法GSA[12]的結果進行比較。為了提高可靠性并產生具有統計意義的結果,在該驗證測試中,所有算法的種群規模都設置為20,維數為30,每種算法都運行30次,函數的最大迭代次數為50 000。表5顯示了5種算法在12個CEC2017函數上的實驗結果,加粗數據表示每個測試函數對應的最佳結果。 Table 5 Comparison of optimization results of benchmark functions in CEC 2017表5 CEC 2017中基準函數的優化結果對比 由表5可知,EGMPA在大多數CEC2017函數上的尋優結果都優于其他4種對比算法的,且取得了較小的標準差,表明了EGMPA的有效性和魯棒性。 本文提出了精英反向學習黃金正弦的海洋捕食者算法,融入精英反向學習機制,使得海洋捕食者算法中的種群質量得到大幅提高,提高了尋優的精度;將海洋捕食者算法和黃金正弦算法相融合,采用黃金分割系數減小海洋捕食者的搜索空間,提高了尋找到最優值的效率。采用經典基準函數和CEC2017函數對改進后的海洋捕食者算法進行了驗證。實驗結果顯示,精英反向學習和黃金正弦2種策略大幅提升了海洋捕食者算法的尋優精度和魯棒性。3.3 EGMPA的時間復雜度分析
4 仿真實驗與結果分析
4.1 初始參數設置
4.2 測試函數
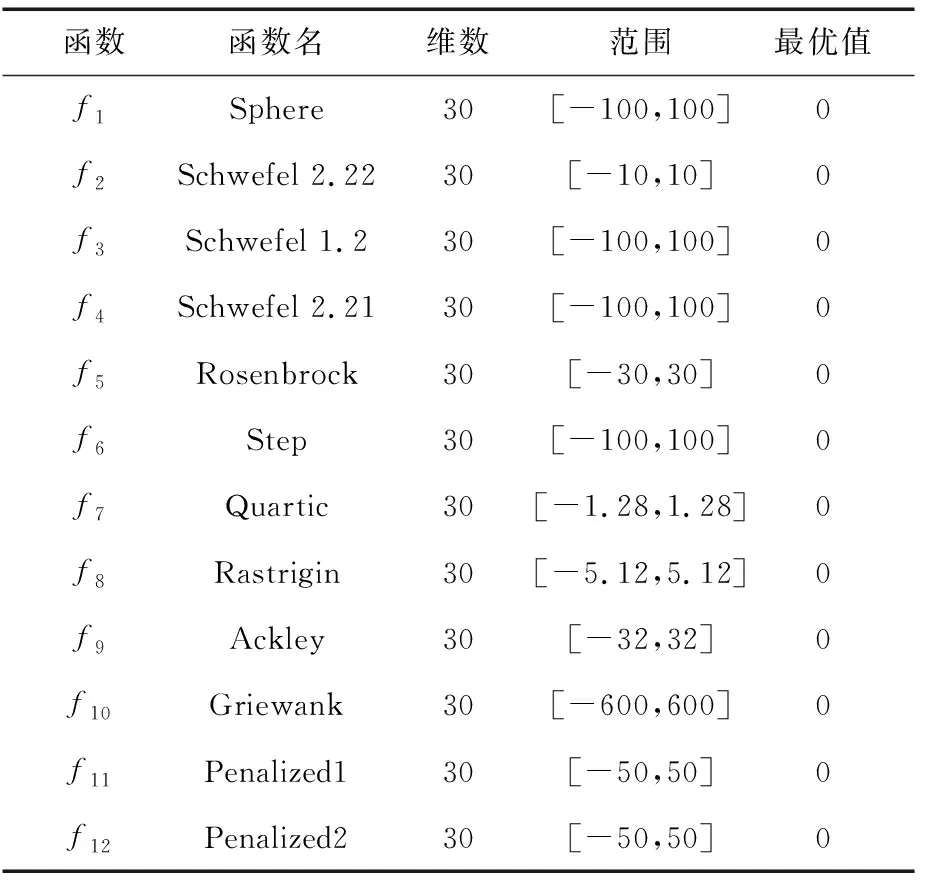
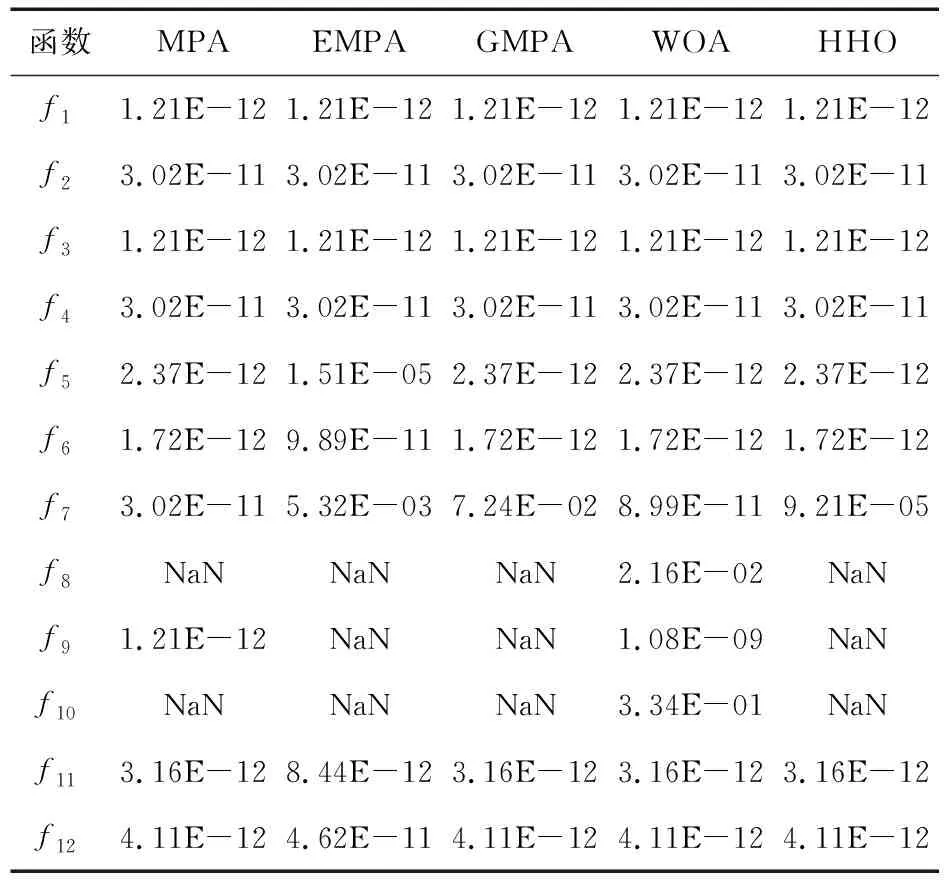
4.3 實驗結果分析

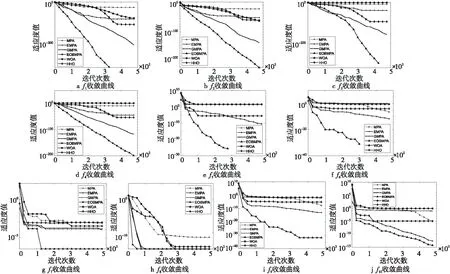
4.4 統計檢驗與MAE 排序
4.5 求解CEC2017實驗
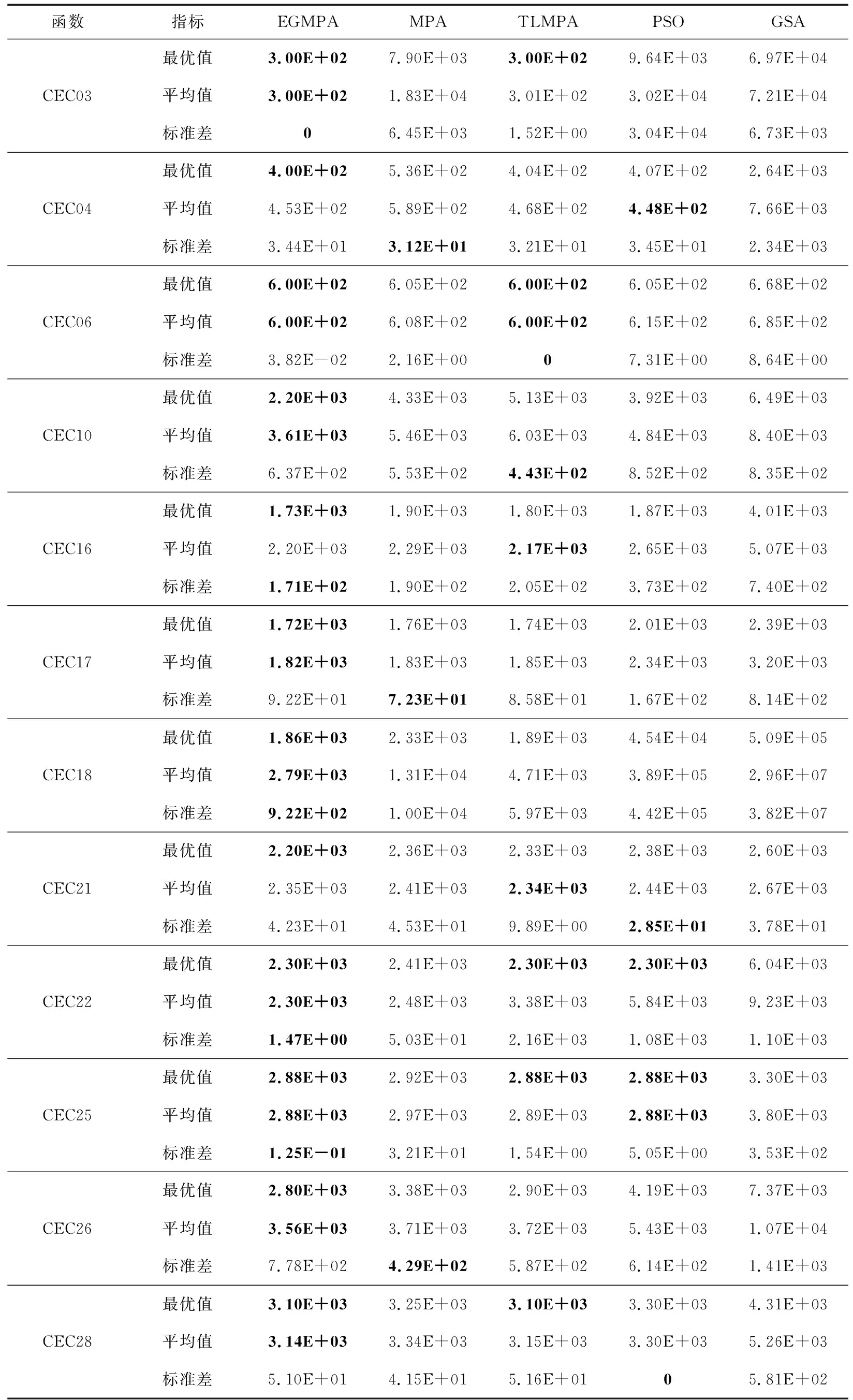
5 結束語

