非接觸式機械密封間隙控制方法及模型研究

周 濤，占宇頡，史偉清

（江蘇大學，江蘇鎮(zhèn)江 212000）

0 引言

由于非接觸式機械密封在運行過程中動靜環(huán)處于不接觸狀態(tài)，具有著端面摩擦磨損小、溫升小、使用壽命長等特點，因此在石化、電力、航空航天等工業(yè)領域有著廣泛應用。其工作原理是通過動（或靜）環(huán)端面微造型動壓槽形成的動壓效應使?jié)櫥ら_啟力增大而保持密封面的非接觸，同時通過泵送槽的泵送作用達到減小甚至阻止泄漏的效果。但在非接觸式機械密封的實際應用中，常因工況波動、軸系振動等多種因素的影響而導致密封端面間隙的不穩(wěn)定，可能出現(xiàn)端面流體潤滑失效、泄漏增大甚至密封環(huán)碰磨損壞等問題。對此，已引起相關專家學者的重視和研究。有文獻指出[1]，早在20 世紀80年代已經有學者對非接觸式密封的動力學響應做出研究，發(fā)展至今已經設計出許多新型的密封結構，取得大量的相關理論成果，但在動力學響應領域，學者在研究時大多考慮單一因素對密封結構的影響，沒有考慮多種因素耦合帶來的影響，因此在面對一些復雜多變的運行工況，這些研究成果難以適用。

綜上所述，目前尚缺乏針對非接觸機械密封端面間隙主動控制方法、途徑等方面的研究，故本文擬針對非接觸機械密封端面間隙不穩(wěn)定問題，基于電磁吸附原理，提出動靜環(huán)間隙液膜厚度主動控制方案，將電磁力引入密封環(huán)受力體系中，通過改變電流調節(jié)電磁力大小，消除潤滑膜壓力變化帶來的影響，實現(xiàn)密封動靜環(huán)間隙的穩(wěn)定及可控。在非接觸機械密封結構基礎上，設計密封間隙控制輔助裝置。采用ANSYS 軟件建立密封間隙液膜內流場數值計算模型并進行仿真計算，結合電磁力計算等對密封環(huán)進行受力分析，研究密封間隙與電磁線圈電流的關系并獲得相應的計算模型，為密封間隙的主動控制提供參考依據。

1 密封間隙主動控制系統(tǒng)設計

基于磁性吸附原理的非接觸式機械密封間隙控制系統(tǒng)如圖1 所示，由環(huán)形銜鐵、電磁鐵、距離傳感器、信號處理器、控制器、可調直流電源及機械密封組件組成。該密封的靜環(huán)為補償環(huán)，動環(huán)端面開設動壓槽，在密封端面運轉中產生動壓效應，使動靜環(huán)分離達到非接觸目的。輔助控制系統(tǒng)主要對靜環(huán)的軸向位移進行控制，可以避免輔助控制系統(tǒng)元件受密封介質的溫度、壓力、腐蝕性等的影響。密封間隙控制系統(tǒng)如圖2 所示。

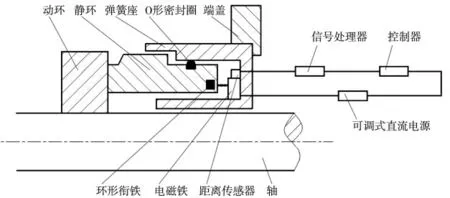
圖1 基于磁性吸附的非接觸式機械密封控制系統(tǒng)

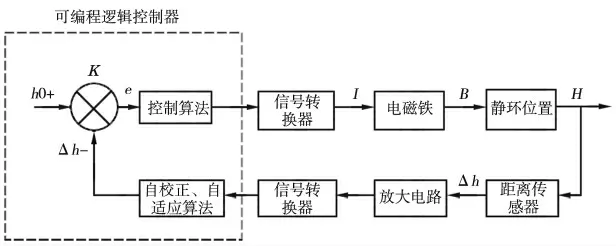
圖2 密封間隙控制系統(tǒng)

環(huán)形銜鐵安裝在靜環(huán)內，在靜環(huán)和電磁鐵間安裝彈簧，靜環(huán)與彈簧座間由O 形圈密封。電磁鐵固定于彈簧座上，可為一個或多個，且與靜環(huán)相隔適當距離。環(huán)形銜鐵為電磁性材料，在電磁鐵通電時與電磁鐵產生相互吸引力，以使機械密封運行時在電磁力、彈簧彈力和端面流體作用力的共同作用下形成密封間隙。距離傳感器安裝于電磁鐵殼體上部，進行距離傳感器與靜環(huán)端面之間間距的測量。距離傳感器測出自身與靜環(huán)端面的距離h，信號處理器根據預設定的h0（未接通電源時傳感器與靜環(huán)的距離）算出動、靜環(huán)端面的間隙Δh。控制器接收信號處理器運算得到的間隙大小Δh，采取PID 控制算法運算得出輸出調節(jié)信號，依據調節(jié)信號控制可調節(jié)直流電源輸出電流I，改變電磁鐵產生的電磁力大小，使靜環(huán)達到新的平衡位置，最終把密封端面間隙調節(jié)到預期大小。

電磁鐵在通電后產生磁場，在密封運轉中，距離傳感器定期測量動靜環(huán)間的間隙寬度，將間距信號通過放大、矯正后轉換成數字信號，并通過PLC 控制器將數字信號轉換成電流信號；再通過整流裝置改變電磁鐵電路中電流的方向和大小，從而改變磁場的方向和大小，以此控制電磁鐵與靜環(huán)上的環(huán)形銜鐵之間的吸引力和排斥力，借吸引力或排斥力來補償開啟力或閉合力的變化。

2 電磁鐵吸附力計算

電磁鐵的吸力是基于麥克斯韋基本方程推導出的，因此需假設磁感應強度B 沿磁極表面是均勻分布的，由此得到電磁吸力的基本計算公式為：

式中 F——電磁吸力，J/cm

B——磁感應強度，Wb/cm2

S——磁極表面總面積，cm2

η——磁導率，此處代入25 ℃液態(tài)水的磁導率，為1.25×10-8H/cm

本文中電磁鐵和銜鐵均為圓環(huán)狀，如圖3 所示，根據該結構做出假設如下[2]：

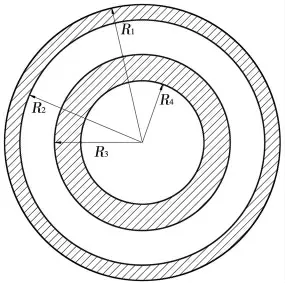
圖3 電磁鐵和銜鐵斷面形狀

（1）不考慮漏磁帶來的影響。

（2）環(huán)形電磁鐵安裝軸不導磁，其磁導率按照空氣磁導率計算。由此建立了磁路等效模型如圖4 所示，得到磁通量計算式為：

圖4 磁路等效模型

其中，IW 為線圈產生的磁動勢；R1為鐵心磁阻；R2為銜鐵磁阻。

因為鐵心及銜鐵的磁導率相對空氣磁導率要大很多，此時只考慮氣隙磁導率的影響，即可以將式（2）簡化為：

其中，G0為氣隙磁導，計算式為：

由所建立的磁路等效模型，還可以得到電磁鐵吸力計算公式為：

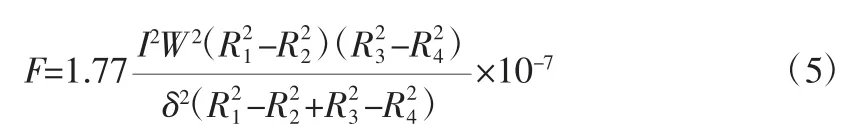
3 液膜壓力的仿真計算和模型有效性驗證

3.1 幾何模型的建立

在動環(huán)低壓側開設N 個螺旋槽，動環(huán)端面呈中心對稱，因此取做為計算區(qū)域，如圖5 所示。在最終計算全周期液膜壓力時，將單周期壓力數值乘以N 即可得到結果。通過CeroE 建立端面密封模型，因為該模型的液膜部分在z 方向上的尺度為微米級，比x、y 方向上的尺度小很多，因此在隨后的ICEM 中進行網格劃分時，利用ICEM 自帶的網格拉伸功能建立完整的液膜模型。

圖5 單周期動環(huán)端面示意

幾何參數和工況參數見表1。

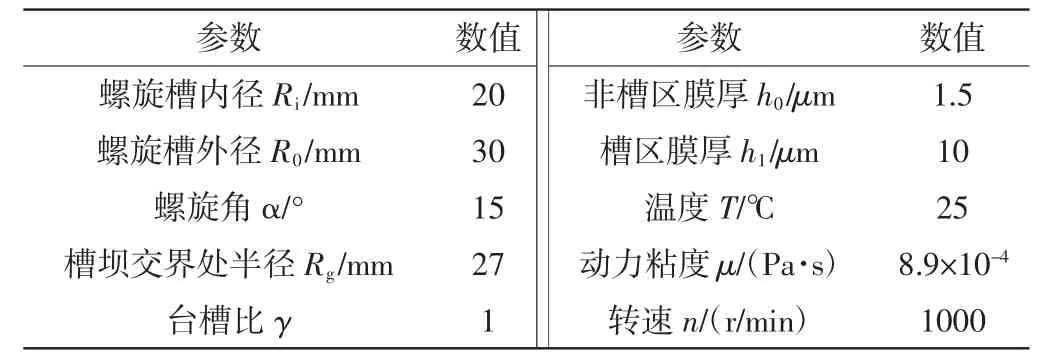
表1 幾何及工況參數

3.2 數學模型

假設潤滑介質的流動是連續(xù)的且密度不變，當槽數趨向無窮多時，上述假設成立。根據窄槽理論[3]，上述假設成立。進一步假設壓力沿槽區(qū)和壩區(qū)呈線性分布，通過求解在槽區(qū)和壩區(qū)建立的微分方程，可以得到壓力分布的表達式。

根據上述假設，在半徑r 處取一寬為dr 的圓環(huán)，圓環(huán)上壓力增量為dp，則對于泵出式螺旋槽，dp 與dr有如下關系式[4]：

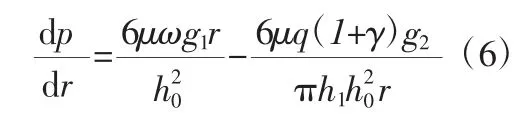
式中 p——螺旋槽液膜壓力

μ——黏度

ω——旋轉角速度

h0——非槽區(qū)膜厚

h1——槽區(qū)膜厚，h1=h0+hg，hg為槽深

g1，g2——螺旋槽系數

γ——臺槽比

q——泵送流量

H——非槽區(qū)膜厚與槽區(qū)膜厚比

α——螺旋線的螺旋角

將式（6）從螺旋槽內徑到某端面位置進行積分，可得到槽區(qū)和壩區(qū)的壓力表達式[5]：

槽區(qū)壓力表達式：

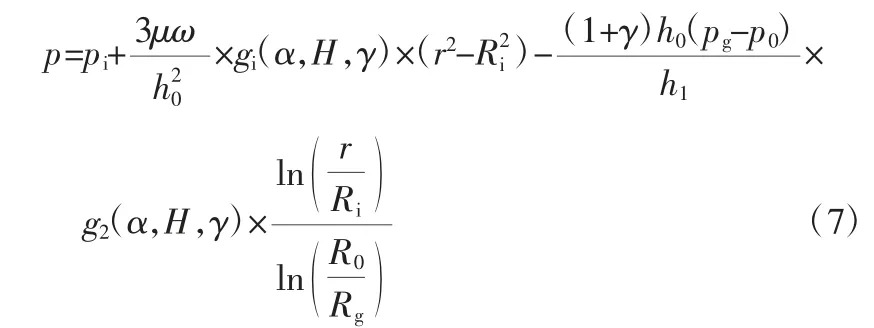
壩區(qū)壓力表達式：

式中pg為槽壩交界處壓力，計算式為：

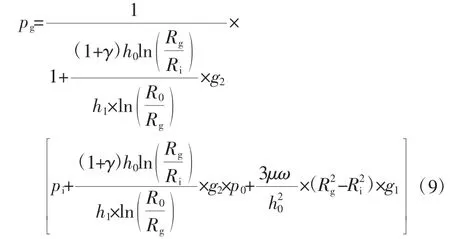
式中 pi——密封環(huán)內側介質壓力

p0——密封環(huán)外側介質壓力

Ri——密封環(huán)內徑

R0——密封環(huán)外徑

Rg——密封環(huán)槽壩交界半徑

3.3 網格劃分及邊界條件

采用Tri 三角形網格單元對垂直于z 軸的表面進行網格劃分，而液膜在z 方向的網格由網格拉伸命令生成，如圖6 所示。

圖6 密封端面部分網格及液膜處的網格拉伸

螺旋槽內液體隨著密封端面的旋轉而運動，槽區(qū)使用Moving Reference Frame，然后設定轉速，壩區(qū)其他設置保持默認。模型進出口端面分別采用壓力進口和壓力出口，其余兩側端面均采用interface[4]，而槽區(qū)壩區(qū)交界處采用interior。

3.4 模型有效性驗證

為驗證本文算法的有效性，采用本文計算方法對文獻［5］的研究對象進行計算，將計算結果同文獻［5］的計算結果進行對比（表2）。取膜厚為1.5 μm，邊界壓力為0 MPa，介質為室溫狀態(tài)下的水。

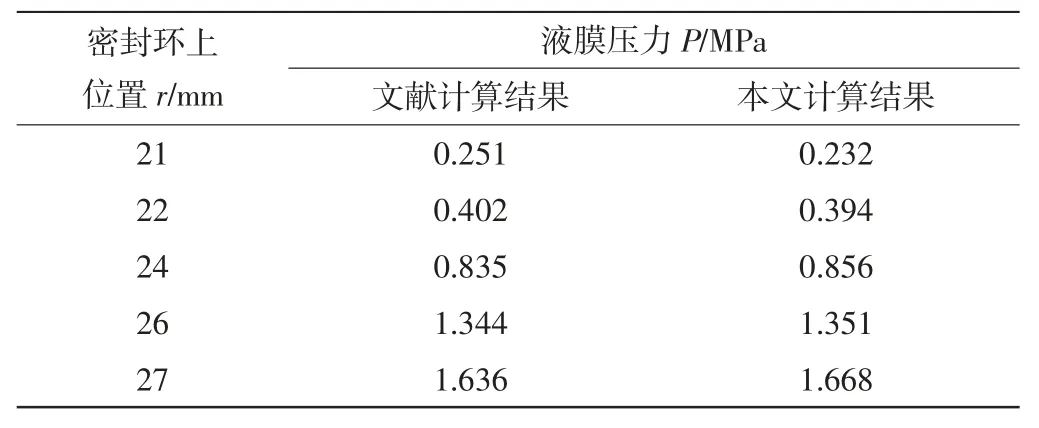
表2 計算結果與文獻［5］結果對比

通過對比可以看出本文計算方法的計算結果與文獻結果相近，且變化趨勢一致，說明本文所使用的仿真方法具有較好的可靠性。槽區(qū)潤滑膜壓力計算結果如圖7 所示。

圖7 槽區(qū)液膜壓力云圖

4 間隙主動控制分析

4.1 控制方程的建立

對圖2 中的靜環(huán)進行受力分析，靜環(huán)受液膜壓力、彈簧彈力、大氣壓力和電磁力的影響。控制方程是在靜環(huán)受力平衡為基礎的條件下得出的，即：

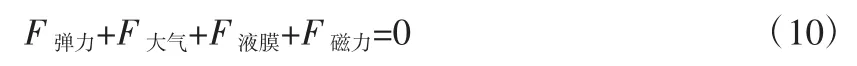
將各項表達式代入得：

式中，k 為彈性系數，Δx0為裝置未工作時彈簧的初始形變量，S 為靜環(huán)周向面積，δ 為液膜厚度。

4.2 控制系統(tǒng)有效性分析

為了確定控制系統(tǒng)的有效性，引入敏感性參數作為判斷指標δ[6]。敏感性參數δ 的定義為：

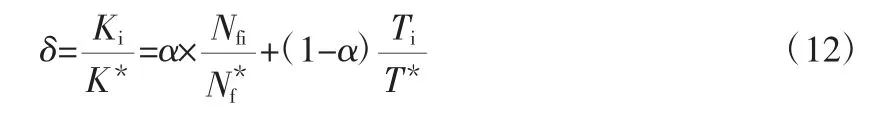
式中，α 為控制量的權重參數，本文認為摩擦力矩與溫度權重相當，即α 取0.5；K＊表示可控型密封在靜態(tài)平衡位置時的閾值；Ki表示可控型密封在時刻i 時的閾值；Nfi和Ti分別表示摩擦力矩、溫度在時刻i 的值和T＊分別表示摩擦力矩、溫度在靜態(tài)平衡時的值。根據張國淵等的研究[6]，利用電磁加載裝置進行主動控制的密封系統(tǒng)的敏感性參數的一般取值范圍為1≤δ≤3.19。在轉速變化的情況下，的值選取其在三種特定轉速（1500 r/min、5000 r/min、10 000 r/min）下的最大值[7]，即1.9、1.1。代入式（12）得到所需的敏感性參數最大值為1.5，小于3.19，說明本文研究的密封系統(tǒng)可以達到主動控制的目的。

5 結論

本文提出非接觸式靜止式機械密封間隙主動控制的方法，設計相應的控制系統(tǒng)，能夠實現(xiàn)密封間隙的有效控制且輔助控制元件不受密封介質的影響，同時，該方法及系統(tǒng)對于類似的間隙控制具有一定的參考價值。建立密封間隙主動控制的數學模型，結合工況變化分析，說明控制系統(tǒng)的有效性。