賦權Myerson值與一致性

單而芳, 聶珊姍, 呂文蓉

(1.上海大學 管理學院,上海 200444; 2.上海大學 數學系,上海 200444)

0 引言

在效用可轉移合作對策中,任何參與者之間都能形成可行聯盟進行合作,并從中獲得合作收益。合理分配參與者間產生的合作收益是保持其穩定合作的關鍵。SHAPLEY[1]根據參與者對不同聯盟的邊際貢獻提出了著名的Shapley值。考慮到在現實中,一些參與者之間不能形成可行聯盟,MYERSON[2]引入圖以描述參與者間的合作通訊結構,將Shapley值推廣到具有圖結構的合作對策(簡稱圖對策)上,提出了Myerson值并給出了公理化刻畫。關于Myerson值最近的其他研究進展可參看LI和SHAN[3-6]、SHAN等[7]。

不過,在實際中不同參與者的討價還價能力可能不同,為此可以根據每個參與者的實力,對其進行賦權以體現參與者的討價還價能力。HAERINGER[8]基于SHAPLEY[9]提出的賦權Shapley值,將Myerson值推廣到賦權圖對策中,提出了賦權Myerson值,并證明它可以由分支有效性和賦權公平性所唯一確定。SLIKKER和VAN DEN NOUWELAND[10]把具有不同權值的參與者看作不對稱參與者,利用分支有效性、類賦權公平性(class weighted fairness)、高階獨立性(independence of higher classes)和類一致性(class consistency)給出了賦權Myerson值的刻畫。最近,WANG和SHAN[11]進一步討論了賦權Myerson值的分解性質。

一致性公理最早由HART和MAS-COLELL[12]在1989年提出,并被用來刻畫Shapley值。此后,該性質被廣泛應用于值的公理化刻畫中。WINTER[13]將一致性應用于到具有聯盟結構的對策中,用一致性和其他四個性質刻畫了著名的Owen值。DRANGAN[14]受HART和MAS-COLELL[12]研究的啟發,構造了Banzhaf值的縮減對策,并據此提出了與該縮減對策相對應的一致性公理,用一致性和標準性給出了Banzhaf值的刻畫。ALBIZURI和ZARZUELO[15]則將一致性推廣到超圖對策上,提出了對應于圖對策的CS-一致性公理,并仿照Shapley值的潛能函數[12]定義了Myerson值的潛能函數,然后借助潛能函數,用CS-一致性和CS-標準性刻畫了超圖對策上的Myerson值。

本文的目的是用一致性公理來刻畫賦權Myerson值。一般地,利用一致性公理來刻畫對策的值時,需要借助潛能函數做工具才能完成值滿足一致性的證明。本文在提出賦權圖對策上的縮減對策和縮減圖后,避開潛能函數的概念,直接建立了在賦權Myerson值下每個聯盟在縮減圖限制對策和原圖限制對策下紅利之間的關系式,由此證明了賦權Myerson值滿足一致性,并最終利用權意義下的一致性和標準性給出了賦權Myerson值的刻畫。

下一節介紹本文所涉及的概念、記號和術語。第三節首先提出賦權圖對策中的縮減對策、縮減圖概念和一致性公理,其次建立聯盟在賦權縮減圖限制對策和原賦權圖限制對策下紅利之間的關系式,然后利用權意義下的一致性和標準性給出賦權Myerson的公理化刻畫。最后一節對本文進行了總結。

1 預備知識

1.1 TU-對策和Shapley值

效用可轉移合作對策,簡稱TU-對策,由二元組(N,v)構成,其中N={1,2,…,n}表示參與者(player)的集合,通常稱為N大聯盟,v表示特征函數(characteristic function),它是定義在N的冪集2N上的一個實映射,并且規定v(φ)=0。N的任意子集S稱為聯盟,v(S)表示聯盟中的參與者進行合作所產生的效用(worth),用|S|或s表示聯盟的基數。將N上所有TU-對策的集合記作GN。以下提到的對策均指TU-對策。

對于S∈2N{φ},對應于S的一致性對策(N,uS)[1]定義為:若S?T,則uS(T)=1,否則uS(T)=0。任意TU-對策(N,v)都可以用一致性對策唯一線性表示[16],即

(1)

其中ΔS(v)為聯盟S的Harsanyi紅利,其表達式為

(2)

在TU-對策(N,v)中,x=(x1,…,xn)∈Rn表示一個支付向量,其中xi表示第i個參與者所獲得的支付。分配規則φ是定義在GN上的一個函數,也即φ:GN→Rn,φi(N,v)表示給參與者i∈N的支付。

在TU-對策中,最著名的分配規則是Shapley值[1],其紅利表達式為

參與者i的Shapley值等于包含它的每個聯盟紅利的均值之和。

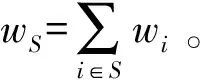
(3)

在合作對策理論中,Shapley值已被廣泛應用于許多領域,對社會、政治、經濟和科學等領域的發展均產生了深刻影響。此外,根據不同的實際背景,它已被推廣到諸如優先聯盟合作結構、通訊圖合作結構等不同的合作結構環境中。

1.2 圖對策和賦權Myerson值

1977年,MYERSON把Shapley值推廣到具有通訊圖結構的合作對策中,提出了著名的Myerson值[2]。下面介紹相關的概念。

一個圖由二元組(N,L)表示,其中N是頂點的集合,每個頂點代表一個參與者,L?LN={{i,j}|i,j∈N,i≠j}是邊的集合,代表參與者之間的通訊聯系。為方便起見,本文用ij代替{i,j}來表示邊。如果ij∈L,稱i和j在圖中是直接連通的。對于不直接相連的參與者i和j,也可能通過其他參與者作為“中介”實現連通。如果存在一條路(path),也就是參與者序列(i1,i2,…,it),i1=i,it=j,使得對于所有k∈{1,2,…,t-1}有{ik,ik+1}∈L,則稱i和j是連通的。這條路也稱為i-j路,路的長度定義為該條路上邊的個數。若圖中任意兩點均是直接連通或連通的,則稱這個圖是連通的。在圖(N,L)中,每個極大的連通子圖稱作一個分支,用N/L表示圖(N,L)所有分支的集合。對任意S?N,由聯盟S導出的子圖記作(S,LS),其中LS={ij|ij∈L,i,j∈S},用S/LS表示S所有分支的集合。如果(S,LS)是連通的,則聯盟S是連通的。

一個圖對策由三元組(N,v,L)所構成,其中(N,v)是一個TU-對策,而(N,L)是一個圖,用CSN表示N上所有圖對策的集合。MYERSON假定每個連通聯盟才是可行聯盟,并在此假設下引入了圖限制對策(N,vL)[2],其中特征函數vL定義為

(4)

MYERSON把圖限制對策(N,vL)的Shapley值作為一個分配規則,這就是著名的Myerson值[2],其表達式為μi(N,v,L)=Shi(N,vL)。

(5)

像引言中提到的,HAERINGER證明了賦權Myerson值可以由分支有效性和權公平性所唯一確定。而SLIKKER和VAN DEN NOUWELAND利用分支有效性、類賦權公平性、高階獨立性和類一致性給出了賦權Myerson值的不同刻畫。

2 一致性與公理化刻畫

2.1 一致性

一致性公理在值的公理化刻畫中具有重要的作用,為完成賦權Myerson值的公理化刻畫,我們首先引入賦權縮減圖對策和縮減圖的定義。

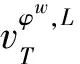
(6)

這里的Tc=NT表示T的補集,也即不在聯盟T中的參與者,而w|S∪Tc表示權向量w在S∪Tc上的限制。賦權縮減圖對策的含義為:在賦權縮減圖對策下,聯盟S的效用等于聯盟S與所有離開的參與者在賦權圖限制對策下進行合作所產生的效用,減去所有離開的參與者按照原分配規則φw所分得的收益和。

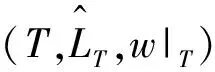
(7)

這里N(P)表示路P上參與者的集合。賦權縮減圖的邊包含兩部分,一是由T導出的子圖的邊,也即LT。二是新增加的邊:若T中的兩個參與者能由T之外的參與者形成的路所連結(除T中的這兩個參與者外,路上的其他參與者均在Tc中),則在這兩個參與者之間增加一條邊。

在定義了賦權縮減圖對策和縮減圖的基礎上,現提出權意義下的一致性公理。

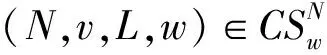
則φw稱具有w-一致性。

2.2 賦權Myerson值的公理化刻畫

為了證明賦權Myerson值滿足w-一致性,根據上一小節所定義的賦權縮減圖對策和縮減圖,本小節首先給出一個關鍵的引理。這個引理給出了在賦權Myerson下任意聯盟S?T在賦權縮減圖限制對策和原賦權圖限制對策中的紅利關系式。

引理1設(N,v,L,w)為任意的賦權圖對策,T?N,則對任意的S?T,S在賦權縮減圖限制對策的紅利值滿足

下面利用上述引理證明賦權Myerson值滿足w-一致性。

為最終給出賦權Myerson值的公理化刻畫,我們需要引入下面的w-標準性。

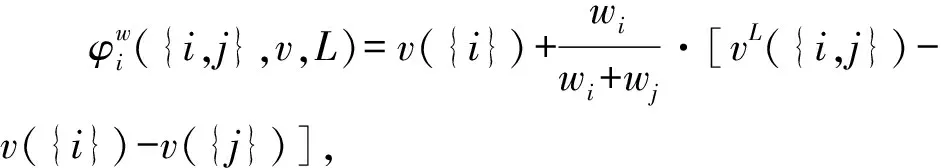
w-標準性的含義為:對于一個兩人賦權圖對策,若兩個參與者不連通,則每個參與者所獲得的收益為自身產生的效用。若兩個參與者連通,則每個參與者先獲得自身產生的效用,再將剩余效用按照自身權重與總權重的比例進行分配。容易證明賦權Myerson值滿足w-標準性。

在利用w-一致性和w-標準性給出賦權Myerson值的刻畫之前,我們首先證明,若分配規則滿足w-一致性和w-標準性,則其一定滿足分支有效性。

3 結論

本文研究了賦權圖對策中賦權Myerson值的公理化刻畫問題,用一致性公理給出了賦權Myerson值的新的刻畫。為達到此目的,提出了賦權縮減圖對策和縮減圖的定義及賦權意義下的一致性公理。通過建立每個聯盟在賦權縮減圖限制對策和原賦權圖限制對策中的紅利關系,證明了賦權Myerson值滿足一致性,從而避開以往文獻中需要借助潛能函數才能完成的滿足一致性證明。最后用w-一致性和w-標準性給出了賦權Myerson值的公理化刻畫。