超低品位磁鐵礦礦巖破碎能耗優化研究

杜廣盛 武海龍 高云峰 陳世江

(1.內蒙古科技大學礦業與煤炭學院,內蒙古 包頭 014010;2.內蒙古自治區礦業工程重點實驗室,內蒙古 包頭 014010;3.烏拉特前旗元大商貿有限責任公司,內蒙古 巴彥淖爾 014400)

礦巖破碎是露天礦開采及加工過程中的主要能耗之一。采下的礦石須經粗碎、細碎等環節進行選礦作業,剝離的廢石若能進行充分利用既可減少堆棄場地,又有一定的經濟效益。在礦巖破碎過程中,其能耗指標是影響經濟效益和綠色生產的主要因素之一。不少學者在研究破碎能耗的過程中,通過對現場實際破碎效果及能耗情況的分析得出了三大破碎功耗理論[1-4],分別從面積、體積、裂縫的角度,對巖石破碎過程中的功耗進行了統計并得出相應的經驗計算公式,明確了破碎能耗與破礦粒度及礦石強度性質的關系。基于此,本研究重點分析巖石物理力學屬性參數與破碎能耗的關系,以及礦山實際設備不同破碎比的能耗規律,進而優化破碎粒度,降低礦巖破碎能耗。

對于巖石物理力學屬性與破礦能量問題,謝和平、鞠楊等學者[5-7]對巖石破碎能量耗散體系進行了分析,提出了基于能量耗散原理的巖石強度理論與破壞準則,強調了巖石破碎是由于外部能量輸入使得巖石內部產生了損傷所致,認為巖石本身物理力學屬性與其破壞時耗散的能量存在很大關系。然而巖石破碎過程中具體的能耗情況影響因素極為復雜,且試驗檢測手段受限。鑒于此,部分學者通過聲發射等能量監測手段對巖石破碎過程中的能量進行監測和分析[8-10],有效確定了外部輸入能量的轉移傳遞情況,明確了巖石質量與聲發射能量的關系,為能耗分析提供了依據。近年來,一些學者研究了巖石破壞過程中的能耗情況[11-18],著重分析了不同加載情況下巖石內部能量的耗散利用情況和不同巖石力學屬性對能耗的影響,研究結果表明:巖石質量參數能夠有效表征巖石破碎能耗指標。針對破礦方式和礦石粒度能耗關系的問題,文獻[19-23]分別研究了破礦顆粒分布及破礦方式和能耗情況,結果表明:不同破礦方式和顆粒特征都會對破礦能耗有所影響,但整體上單次破碎比與能耗呈正相關,且單次破碎比越大,能耗越高。

基于上述成果,結合某露天礦山實際情況,本研究針對不同礦巖進行力學試驗從而構建礦巖質量參數,并引入破碎能耗公式求解能耗指標,進而對礦山能耗進行優化分析。同時以礦山實際設備為基礎,分析多級破碎中的能耗規律,并對能耗指標進行求解,較為準確地優化礦山破碎能耗。

1 巖石力學試驗

不同力學性質巖石破壞時的能量消耗有較大差異,為此,本研究對該礦山采場采出的礦石和上下盤巖石分別進行了力學性質試驗。由于破礦形式有所不同,對巖石進行了單軸抗壓、巴西劈裂抗拉、雙軸抗剪等較為全面的測試。

1.1 巖石試件制備

(1)針對礦山不同區域的巖石性質差異,選擇從采場礦體中部平臺上選取部分巖體,在地質圖上對應其巖性,并對上下圍巖和礦石進行分類。對取回的巖石進行加工,以制成符合實驗室單軸抗壓試驗要求的試件。

(2)巖樣加工過程中將切割機刀片相對位置調整為100 mm,切割后獲得上下端面較為平整的巖塊;然后利用立式取芯機在規整的巖塊表面進行鉆取切割。為保證制備的試件完整且尺寸和表面條件達標,在取芯的過程中鉆頭給進速度選取4 mm/min;最后采用端面磨平機對試件兩端面進行平整度校準。試件高徑比保持為2∶1,直徑誤差不超過0.3 mm,兩端面平整度誤差保持在0.05 mm以內。試件制備過程及結果見圖1。

圖1 試件制備過程Fig.1 Preparation process of specimens

1.2 巖石力學性質測試試驗流程

(1)單軸抗壓試驗。巖石單軸抗壓強度采用wance106微機控制電液伺服萬能測試機進行測定,最大垂直加載力為1 000 kN,試驗采用壓力控制方式,初始加載給入壓力設置為100 N,壓力速度為500 N/s,破壞力識別為15%,在到達極限載荷強度時自動卸載5 s,以保證試件破壞后及時撤去加載力。

(2)巖石單軸壓縮變形試驗。采用應變數值采集儀、應變片、位移采集器等記錄試件在加載過程中的形變狀態。分別將應變片貼在巖石試件表面,垂直和水平方向均進行了監測。

(3)巖石巴西劈裂抗拉強度試驗。采用巴西劈裂測定巖石抗拉強度,根據要求的劈裂方向,通過試件直徑的兩端,沿軸線方向畫兩條相互平行的加載基線,將試件放置在加載板上,調整中心位置,使試件不產生應力集中,以0.3～0.5 MPa/s的速度加載直至破壞。

(4)巖石雙軸抗剪強度試驗。將制備好的試件放置在剪切模具中,模具由硬質合金鋼制成,具有較高的強度,變形量很小。本次試驗保持一致的法向力,設置為2 kN;當法向力穩定后再加載切向載荷,不斷對切向載荷進行監測,以0.05 mm/s位移進行加載直至破壞。

圖2 巖石力學試驗Fig.2 Rock mechanics test

1.3 試驗結果分析

根據測試結果,分別進行單軸抗壓強度、抗拉強度、抗剪強度、彈性模量等指標計算。

單軸抗壓強度計算公式為

式中,σc為巖石單軸抗壓強度,MPa;P為最大破壞載荷,N;A受載試件的橫截面積,mm2。

彈性模量計算公式為

式中,E為彈性模量,GPa;σ為應力,MPa;ε為應變,可進行如下計算:

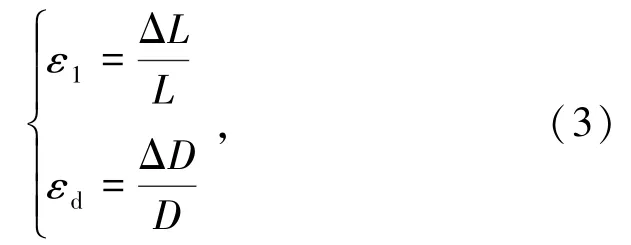
式中,ε1為各級應力的軸向應變值;εd為與ε1同應力的徑向應變值;ΔL為軸向變形平均值,mm;ΔD為徑向變形平均值,mm;L為試件高度,mm;D為試件直徑,mm。

抗拉強度計算公式為

式中,σt為巖石抗拉強度,MPa;P為試件破壞載荷,N;D為試件直徑,mm;h為試件厚度,mm。

抗剪強度可進行如下計算:

式中,τ為作用于剪切面上的剪應力,MPa;P剪為剪切載荷,N;A剪有效剪切面面積,mm2。

根據式(1)至式(5),相關參數計算結果見表1。

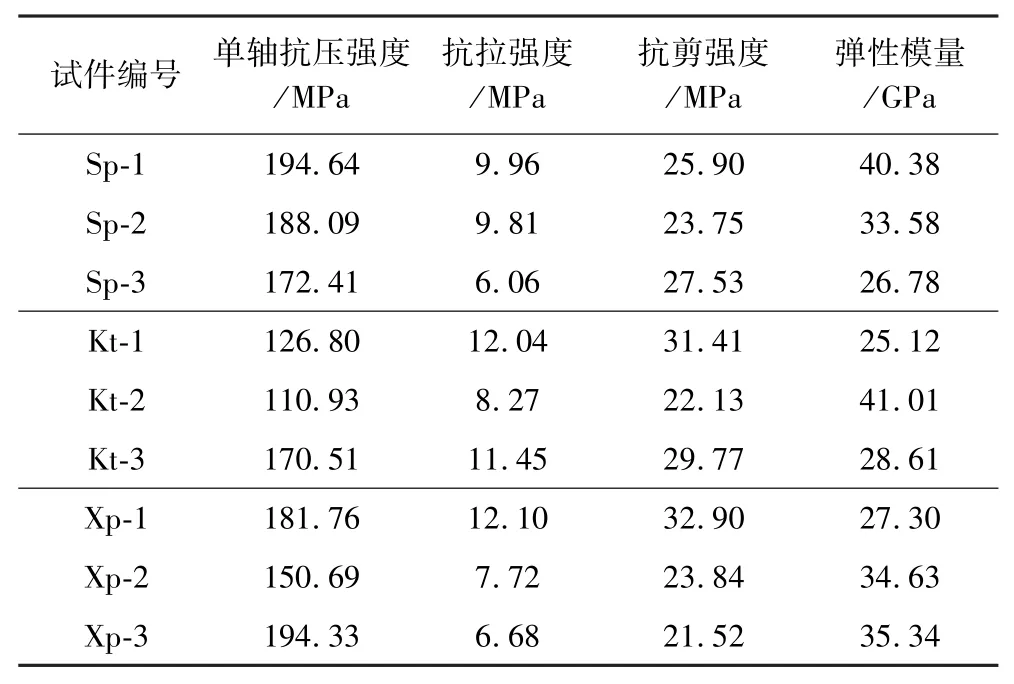
表1 巖石力學性質試驗結果Table 1 Test results of rock mechanical properties

對計算結果進行了統計,3組試驗取平均值如圖3所示。其中,試件組1、2分別為上下盤圍巖分組,試件組3為礦石分組,上下盤圍巖單軸抗壓強度明顯大于礦石強度,且礦石強度約為圍巖的75%;彈性模量變化趨勢與單軸抗壓強度相同,也呈現圍巖彈性模量大于礦石的特征。

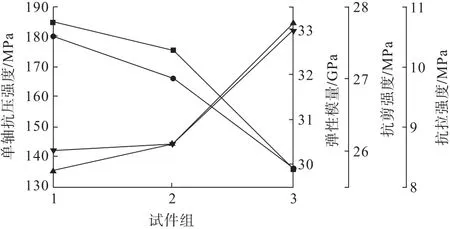
圖3 不同礦巖力學參數對比Fig.3 Comparison of the mechanical parameters of different minerals and rocks

由圖3可知:相對于上下盤圍巖,礦石單軸抗壓強度較低但抗拉強度和抗剪強度較高,說明礦石相對圍巖顯延性;而圍巖單軸抗壓強度較高,抗拉和抗剪強度較低,說明其顯脆性。

2 礦石破碎能量分析

巖石在破碎過程中需要受到外部的能量輸入才能進行相應的失穩開裂,不同的擠壓破碎方式所輸入的能量也有所不同,不同的開裂形式所吸收的能量也有較大區別,并且巖石的物理力學性質對能量輸入和保存也有一定的影響。近年來,部分學者從能耗角度對巖石破碎能量理論進行了分析。

2.1 破巖能耗理論

2.1.1 吉爾皮切夫和F.基克學說——體積學說

礦石破碎過程中具有形變儲能等作用,在礦石破壞后其整體體積沒有發生改變而形態有所變化。設A為礦石破碎所需能量與其體積或質量的比值,對于單位體積巖塊,其計算公式為[2]

式中,k1為比體積功,產生一個單位體積形變所做的功;Δv為微元破碎體積變化量。

將破碎過程視為多次破碎的疊加,可以推導出:

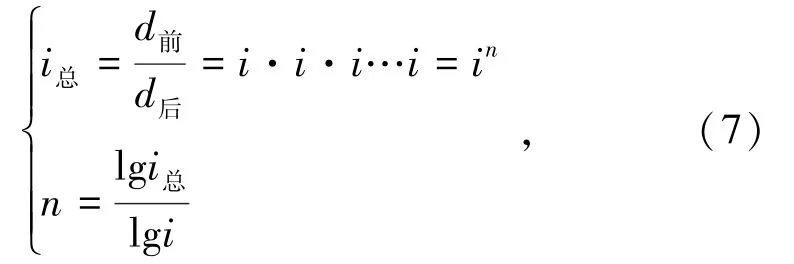
式中,i總為總破碎比;i為微分每級破碎比;d前、d后為破碎前后粒徑,mm;n為微分的破碎級數。

當破碎一定體積礦石時,礦石總體的體積變化量可表示為

將式(8)代入式(6)中可得總破碎功耗情況:

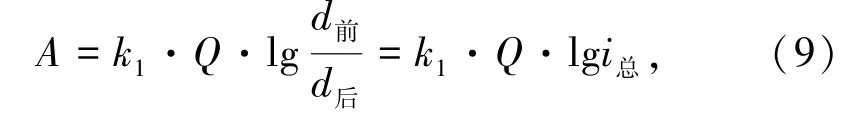
式中,Q為進料體積,m3。

破碎物料通常為混合物料,可通過下式求出單一礦石能耗W對k1進行優化:

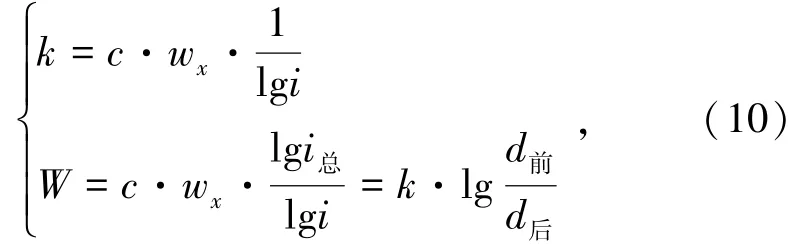
式中,k為破碎功參數;wx為每級能耗,J;W為總能耗,J;c為巖塊強度屬性參數。

在巖石破碎過程中k礦、k巖受巖石本身物理力學屬性影響,將式(11)參數按順序代入式(12)中可以求得k1關于σ和E的表達式。對k1進行分析求解可以得出式(13):

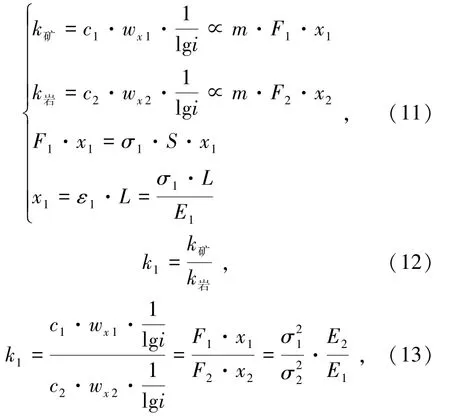
式中,F1、F2分別為不同巖塊載荷,N;x1、x2為作用力下的位移,mm;σ1、σ2分別為巖塊強度;S為試件受力面積,mm2;L為試件位移方向的尺寸,mm;E1、E2為試件彈性模量;m為比例系數。

可以看出k1受巖石單軸抗壓強度σ和彈性模量E的影響,因此在巖塊強度屬性存在差異時會對整體破碎能效產生影響。

2.1.2 F.C邦德及王文東裂縫學說

根據碎礦、磨礦設備試驗得到的資料[2],整理成如下經驗公式:

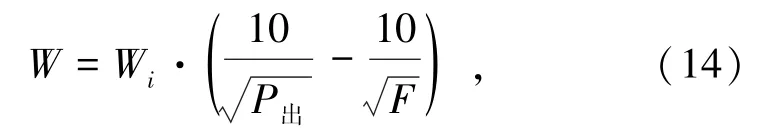
式中,Wi為邦德功指數,是當物料尺寸為0.1 mm時的功耗;F為進料尺寸,mm;P出為出料尺寸,mm。

通過球磨機試驗進一步確定Wi值:

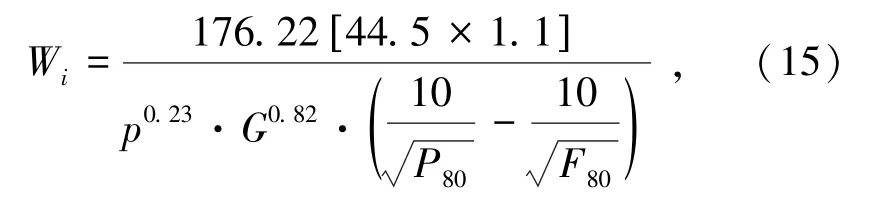
式中,p為篩孔尺寸,mm;G為新生篩下物料質量,g;P80、F80為出料和進料80%過篩尺寸,mm。

通過對礦石的試驗可以得出p為0.15 mm;G約為4 g;P80、F80分別為0.125、3.3 mm;最終計算得Wi約為20。

2.2 巖石力學性質評價

經過本研究試驗得出,礦石和圍巖的力學性質分別表現為延性和脆性。選取巖石力學性質中抗壓強度σc與抗拉強度σt的比值作為評價巖石脆性和延性的指標b,即b=σc/σt。代入試驗數據計算可得,b值分別為21.54、12.89、20.34。由式(13)可以看出σ為巖塊強度,當采用混合經驗公式時可以將巖石脆性指標b作為平均指標代入公式中。即σ1/σ2=b1/b2。此時利用巖石物理力學性質參數選取單位強度1進行對比,可以進一步求出3種不同巖性的k1值分別為14.12、5.54、12.97。由k1值的變化可以看出,當其他參數不變時,破碎圍巖的能耗遠大于破碎礦石的能耗。

2.3 礦巖初破不同粒徑能耗分析

根據礦山破碎設備的實際情況,可知在初破工序時,進料巖石塊度平均尺寸為400 mm,出料口為95～165 mm。

通過破碎機理可知,在破礦形式不變的條件下,破碎料強度也保持一致時,k1、Q值取1。破礦能量受礦物顆粒變化影響。由粗料破碎理論式(9)可知,出料粒徑為95 mm時A為66.62;當出料粒徑為165 mm時A為29.55。此時可以看出破礦粒度對能耗影響非常大。

對不同出礦粒度進行分析,結果如圖4所示。由圖4可知:隨著出礦顆粒增大,能量消耗比逐漸減小,出礦顆粒為165 mm和95 mm時能耗比為29.55和66.62,并且減小速度降低,即出礦顆粒從95 mm變化為100 mm時能耗比降低了4.37,而出礦顆粒從160 mm變化為165 mm時能耗比降低了1.57。

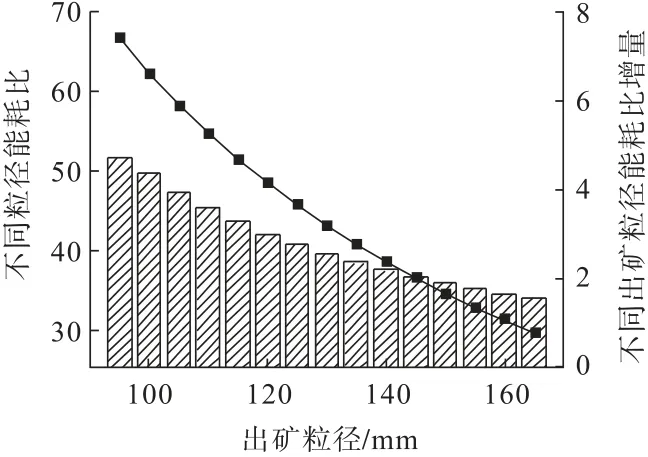
圖4 出礦粒度與能量耗散比的關系Fig.4 Relationship between ore size and energy dissipation ratio

2.4 礦巖多級破碎不同粒徑能耗分析

根據礦山實際破礦工藝及設備參數可知,主要產出為一定粒徑的石子,因此本研究采用F.C邦德(Bond)及王文東裂縫學說(1952)[2]分析式(14)發現,顯然該公式受到巖石力學性質和巖石破碎塊度影響,當Wi取20且保持不變時,能耗受塊度比變化的影響。分別將不同的粒徑代入式(14)進行計算可以得到如圖5所示的變化曲線。由圖5可知:粒徑差值越小能耗越低,隨著粒徑差值逐漸增大消耗過多的能量無法將顆粒進一步破碎,造成一定的能量損失,因此選取逐級破碎效果更好。

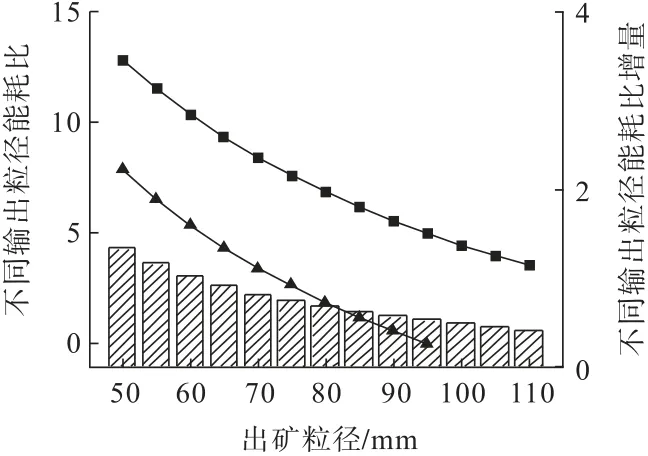
圖5 出礦粒度與粒度差值能耗比關系Fig.5 Relationship between ore size and energy consumption ratio of particle size difference

2.5 礦巖破碎總能耗優化

針對礦山實際工程需求,該礦山后續破碎共分為4級,且隨著不同破碎工藝產出不同粒徑的石料。破碎后最終產出物料為3 mm石子,因此后4級總破碎比i總=3/d1,其中,d1為初破后的顆粒尺寸。通過對圖4、圖5分析可知:當單極破碎過多時會大量消耗能量。當進行初破之后,將后續4次破碎粒徑平均分布在整個工藝中,即破碎比i總=(i單)4。而初破后不同的粒徑對后續破碎有著較大影響,當d1為95～165 mm可以求得i總為1.82%～3.16%,此時i單為36.7%～42.2%。通過式(14)求得后續4級能耗。由于初級破碎與后4級破碎設備的差異,通過礦山數據調查得出初破與后續破碎能量利用率分別為0.8和1.5。因此對初級破碎能耗進行加權求和可得出整體工藝能耗比情況,如圖6所示。由圖6可知:當初破粒度為125 mm時,后續破碎保持40%左右的破碎比時能耗比最低。

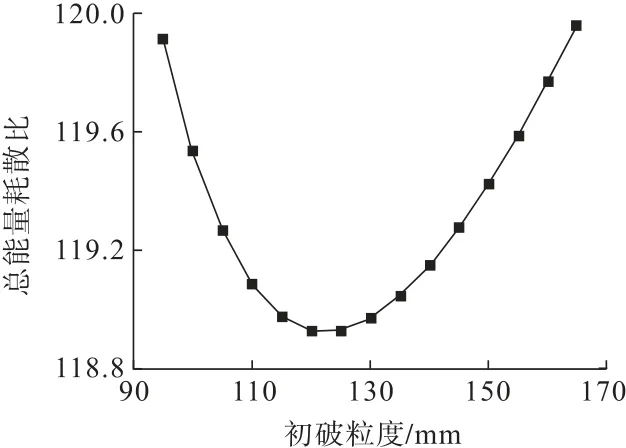
圖6 不同初破粒度下總能耗比Fig.6 Total energy consumption ratio under different initial breaking particle sizes

3 結 論

針對礦山礦巖破碎的能耗問題,以內蒙古中部地區某露天礦為例,采用室內試驗對礦巖質量進行了測定并結合礦巖破碎理論,進一步分析了礦巖質量與多級能耗間的關系。所得結論如下:

(1)通過對經典能耗公式中引入結合了巖石強度與脆性參數的巖石質量參數b,有效地計算出不同質量參數礦巖在破碎過程中的能耗指數,為能耗優化提供了更為合理的依據。

(2)通過對不同礦巖進行試驗可以計算出巖石質量參數b,結合礦山實際破碎工藝采用經典能耗公式進行計算,可以得出破碎圍巖能耗高于破碎礦石,應分時段破碎;在多級破碎能耗優化中,礦巖初破應破至125 mm,后續多級破碎時應破碎至當前粒徑的40%左右時能耗較低。

(3)結合實際生產情況,不同的破礦形式被用于不同的破碎階段,這與礦巖質量共同構成了破碎能耗指標,而常用的能耗公式中對此研究不足,因此結合破碎形式和礦巖質量的修正系數對能耗指標的表征更為精確。