基于改進的粒子群優化神經網絡算法的海平面變化預測分析

張 宇 賀小星 孫喜文

(1. 江西理工大學 土木與測繪工程學院, 江西 贛州, 341000;2. 東華理工大學 測繪工程學院, 江西 南昌, 330013)

0 引言

導航、海污染擴散建模以及海域能源勘測等工業用途都需要海洋空間域上的精確潮汐預報[1-2]。由于潮高受到海水溫度,鹽度、陸地水體以及地球物理過程等因素的聯合影響,低、高潮位之間并不是總是反相變化,而是正反相交替變化,這也使得一些經典模型在潮位預報中得不到較好的精度。

本文基于分群思想,構建了一種多個分群間協同進化的智能粒子群優化網絡模型(swarm strategy particle swarm optimization-back propagation,SSPSO-BP),通過建立多個具有信息交流能力的分群及在粒子進化進程中引入“變異算子”,采取自適應慣性權重調整策略在搜索過程指引粒子走向全局最優解,來實現智能化的參數搜索。針對日本沿岸在PSMSL網站上Oga站的連續月數據,SSPSO-BP模型在潮位預報中與實測值具有高度的一致性,潮位特征的預報準確度較高[3]。

1 BP神經網絡與PSO算法介紹

1.1 BP神經網絡算法原理

BP神經網絡是一種依賴誤差反傳機制的多層前饋網絡。在網絡訓練過程中,通過誤差反傳不斷調整連接參數,使輸出與期望間的均方誤差達到目標精度或者迭代次數達到閾值[4-5]。

BP神經網絡訓練的主要步驟如下。

(1)網絡初始化：選定網絡的輸入層節點數為N,隱含層節點數為H,輸出層結點數為M,設定輸入層與隱含層、隱含層與輸出層神經元之間的連接權值Wij,Wjk及激活函數。

(2)隱含層及輸出層計算。

(3)修正連接權值。

(4)判斷全局誤差或學習次數是否滿足要求,若滿足則訓練結束,否則繼續選取樣本輸入及期望輸出,返回到步驟(2)繼續對網絡進行訓練,直至達標。

1.2 標準PSO算法

實際工程問題的解經過編碼后可以看成一個在D維搜索空間的粒子[6]。粒子在搜索域中的速度和位置的更新公式為

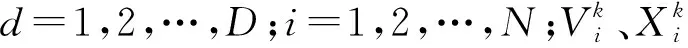
由式(1)、式(2)可知,w越小,粒子飛行時的迭代步長越小,越趨向細致的局域搜索;w越大,粒子飛行時的步長越大,粒子越趨向于寬泛的全局搜索。常見的慣性權值調整策略為

式中,t為當前迭代數;tmax為最大進化次數。

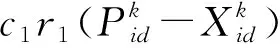
1.3 基于分群策略的粒子群改進算法

基于分群策略的粒子群改進(particle swarm algorithm based on swarm strategy,SSPSO)算法(圖1)將粒子分為基礎群Q1、Q2、綜合群Q3三個群體,分群間在同一搜索空間中飛行找尋最優位置,且在搜索過程中保持種群之間的信息交流。同時在粒子進化的過程中保留其自身的思維,使得其能夠依據隔代適應度差異自適應調整慣性權重以及根據進化程度改變學習因子來完成在整個過程中智能調整搜索策略,并且引入變異算子在粒子基本喪失進化能力時進行變異,保持粒子群的種群多樣性,走向智能化的方向[10-11]。

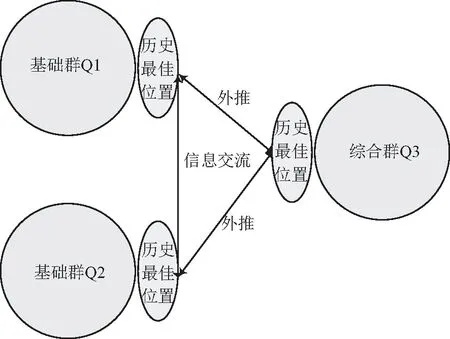
圖1 分群策略示意圖

綜合群S3的進化方程：

(6)

(7)

式中,m1、m2分別為基礎群Q1、Q2粒子的適應度,決定了基礎群的粒子速度對綜合群速度的影響大小。基礎群Q1、Q2進化方程和標準粒子群進化式(1)、式(2)相同。綜合群Q3進化的過程的顧及了基礎群Q1、Q2速度的影響,并保證了適應值高的群體對綜合群有著更大的影響,上述進化模式,利用了所有的分群信息,既保證了群體間的聯又提高了種群的多樣性。

實際搜索過程中粒子軌跡呈現復雜的動態變化,LDI-PSO調整策略(式3)并不能反映實際的搜索過程,并且慣性權重下降的最優斜率受各種因素的影響,常數的變化斜率并不適用于所有的優化問題[12-13]。因此當慣性權重w較小,且fitk與fitk-1的差值小于一個極小的固定值ε時,則說明此時粒子大量聚集,此時采用w=w+rand·w調節慣性權重使其變大,增強粒子的全局搜索能力,使粒子擺脫局部極值。同理慣性權重w較大則表明粒子間的搜索經驗分享不足,此時采用w=w-rand·w減小慣性權重,加強粒子間的信息交流。慣性權重w調整公式為

(8)

整個搜索進程中,當粒子適應度的隔代差值為一個極小數并且以一定距離偏離全局最優,可認為粒子陷入局部最優值,喪失了向全局搜索的能力。為了讓粒子保持向其他區域搜索的活力,使種群避免出現過早聚集的情況,SSPSO算法引入變異算子防止種群出現“早熟”。我們用種群適應度方差σ2來描述種群聚集度,σ2定義為

(9)

式中,fitavg為種群適應度平均值;f為歸一化因子，f=max{1,|fi-favg|}

式中,λ為收斂精度,根據實際問題設定。滿足上述條件的粒子速度降為0,喪失向其他區域搜索的能力,此時引入變異算子,粒子的速度更新公式變為

(10)

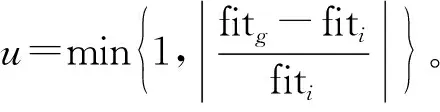
2 基于SSPSO算法的BP神經網絡模型

基于SSPSO優化的BP網絡模型的實現包含如下基本步驟：確定網絡的結構、初始化基礎群和綜合群、計算分群粒子的適應度、依據一定策略更新速度及位置[14-15]。算法實現的流程如圖2所示。

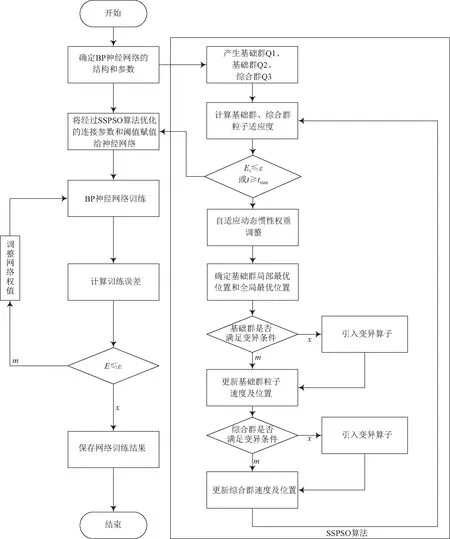
圖2 SSPSO算法優化BP神經網絡實現流程

3 應用實例及結果分析

本文使用的驗潮站數據由PSMSL網站提供,PSMSL成立與1933年,位于利物浦的國家海洋中心,負責全球驗潮站海平面數據的收集、發布、分析及解釋。PSMSL網站發布的資料為RLR格式的數據,RLR版本的驗潮數據分為月平均數據和年平均數據。日本沿岸在PSMSL網站(https://www.psmsl.org/)上約有35個驗潮站,本文利用Oga站2000—2012年的連續月數據進行潮位特征預報。

3.1 SSPSO-BP算法的實現以及結果分析

本文選擇200期的連續月觀測數據代入SSPSO-BP模型中,圖3為兩種模型性能對比。

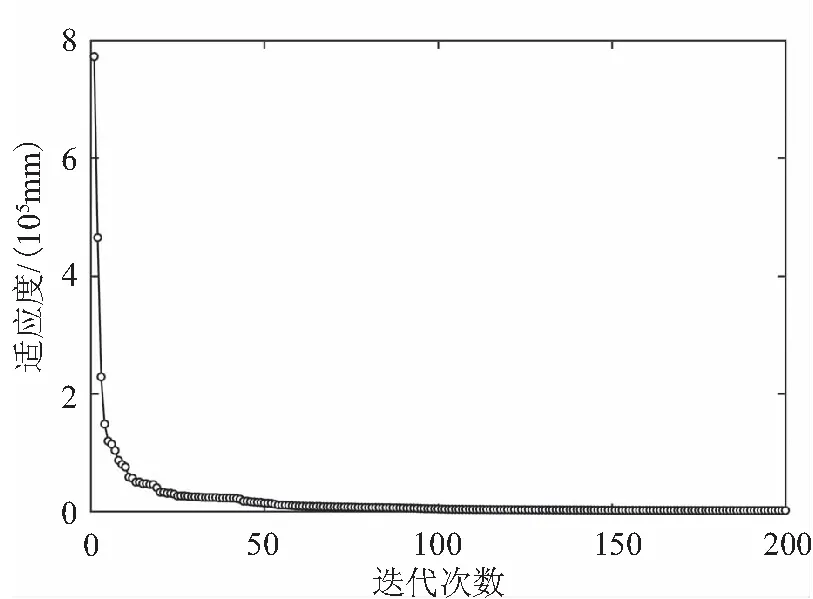
(a)PSO誤差曲線

由表1可知,PSO-BP、SSPSO-BP網絡比標準的BP神經網絡收斂次數明顯減少,引進粒子群算法大大減少了神經網絡的訓練時間。由圖4可以看出,綜合群粒子在進化過程中會依據自身的搜索狀態自適應地動態調整慣性權重以改變搜索策略,增加全局搜索能力,在第376次進化時綜合群中出現粒子聚集現象,群速度降為0,此時慣性權重發生跳變,幫助粒子群繼續向其他區域搜索。另外SSPSO算法引入了變異算子,理論上算法的迭代次數應該增加,但是實際上分群思想保證了粒子種群的多樣性,尋找最優解的能力明顯得到提高,從表中看出,SSPSO-BP模型無論是訓練時間還是均方誤差都相較于PSO-BP模型有所提高。

表1 訓練結果對照

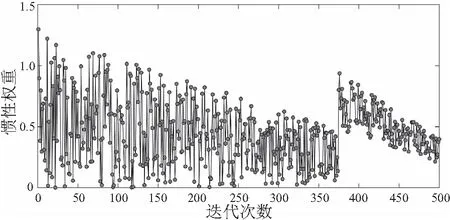
圖4 自適應動態調整慣性權重

3.2 驗潮站潮位預報

以日本沿岸的Oga站為例分析比較后100期潮高預報值與實測值,圖5為Oga站逐月潮位資料。

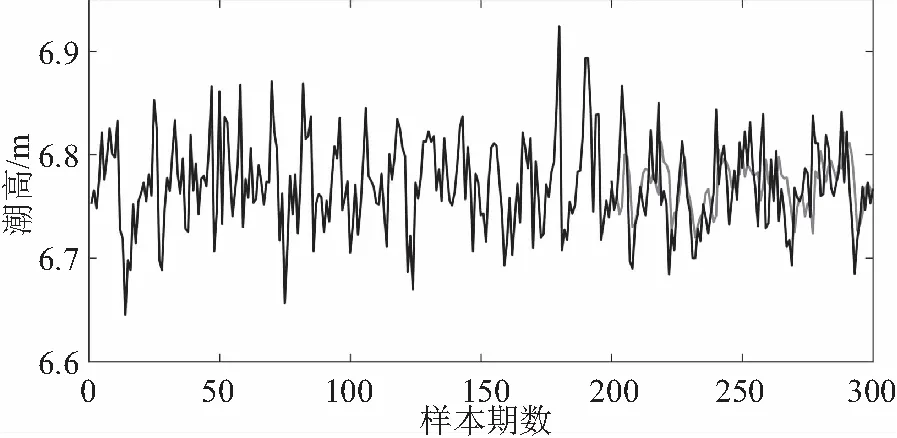
圖5 潮位趨勢預測

海域潮高變化既是海域潮汐性質的體現,也是潮波系統間的作用過程和機制的反映。從圖5可以看出,Oga站上低潮位、高潮位間的關系較為復雜,它們兩者并不是嚴格反相變化,而是呈現正反相交替的變化趨勢。SSPSO模型在采樣頻率小的潮位資料上可以很好地復現潮位變化趨勢,并且高潮位和低潮位時刻基本一致。

利用Oga站2000—2012年里的連續月潮位資料對完成訓練的三種模型進行仿真,并將仿真結果和實測潮高進行對比。對比結果見圖6,兩種模型的性能指標對比結果如表2所示。

圖6可以看出2000—2012年Oga站的潮高長時間處于高潮位,在2010年9月出現了低于平均海水面的低潮位時刻。SSPSO模型在低頻潮位資料上,預測值與實測值的一致性較好,高潮位與低潮位時刻基本對應,高潮時刻最大潮高差為7.37 cm,低潮時刻最大潮高差為4.21 cm,相比標準BP神經網絡及PSO優化神經網絡最大潮高誤差大大減小。另外,SSPSO-BP模型的平均絕對誤差、均方誤差相較于BP神經網絡分別提升了16.2%、79.2%,相較于PSO-BP神經網絡提升了13.9%、79.6%,可以看出SSPSO-BP神經網絡模型對于潮位預報的準確度和精度都有了較大的提升。

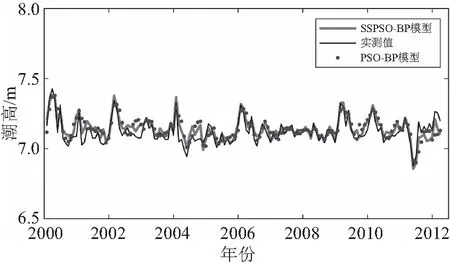
圖6 模型預測曲線對比

表2 三種模型潮高預測誤差對比

4 結束語

SSPSP算法與BP神經網絡結合對BP網絡的初始權值和閾值進行優化選擇,將綜合群的最佳位置作為BP神經網絡參數初值并且通過不斷的學習進行反向調整,最終產生一個經二次優化的參數向量。由于SSPSO算法進行了BP神經網絡的初次尋優,大大減少了BP神經網絡的迭代次數,在潮位預報中能夠很好地預測潮位特征。

(1)基于分群策略的粒子群優化網絡通過分群之間的信息交換以及進化進程中的變異,更加有利于找到全局最優解,相比于傳統模型大大減小了陷入局部極值的概率。在低頻潮位資料的背景下,也能很好地復現海平面變化趨勢,保證高低潮位時刻的一致性。

(2)SSPSO-BP神經網絡模型有效地回避了海域潮汐以及多潮波系統作用等復雜因素的影響,采用線性逼近的思想來模擬多因子的作用機制,在高低潮位的振幅以及對應時刻上保持良好的一致性,在潮高差、潮時差等潮位特征上也有很好的預報效果。