物理驅動深度學習波動數值模擬方法及應用1)

陳 蘇 丁 毅 孫 浩 趙 密 王進廷 李小軍,,3)

* (北京工業大學城市與工程安全減災教育部重點實驗室,北京 100124)

? (中國人民大學高瓴人工智能學院,北京 100872)

** (清華大學水沙科學與水利水電工程國家重點實驗室,北京 100084)

?? (中國地震局地球物理研究所,北京 100081)

引言

近場波動既是地震學和地震工程等領域所關心的關鍵科學問題,也是涉及大型工程地震輸入和抗震分析的重大工程問題.在過去的幾十年里,波動模擬主要采用有限差分法[1-2]、有限元法[3-4]、譜元法[5-7]等,將連續變量的解析問題轉化為離散變量的數值問題.特別是譜元法作為較新的數值算法,不僅具備處理復雜幾何問題的靈活性,還具有偽譜法的高精度性和快速收斂性,在波動模擬中取得了廣泛應用.為了模擬地震波在無限域條件下的傳播特性,各類數值方法對計算模型的空間離散方法和人工邊界的處理方式有很高的要求.求解結果的優劣依賴于網格的剖分,對于復雜波動問題,可能會導致巨大的計算和存儲;其次,所引入的人工邊界的精度和穩定性問題一直以來都是研究近場波動數值模擬的一個重要問題[8-10].近場波動在數學上可歸結為偏微分方程的初、邊值問題,近年來,基于數學物理方法前沿成果的近場波動數值模擬成為熱點.

隨著數據和計算資源的爆炸式增長,數據驅動的機器學習在圖像、自然語言處理等方面取得了很多革命性的成果.高度依賴數據驅動的方法,缺乏物理可解釋性、易陷入過擬合以及可獲取數據的稀疏性等問題,限制了這類方法在諸多學科和工程領域中的應用.人工智能科學范式(AI for science)已成為新的交叉領域,將物理原理與數據相融合,以建立更通用、解釋性更強的機器學習模型,得到了廣泛的關注,比如Deep Ritz 方法[11]、深度Galerkin 方法[12],PINN 方法[13]等.其中,Raissi 等[13]提出了物理信息神經網絡(physics-informed neural networks,PINN),將偏微分方程以及初邊值條件融入到神經網絡的損失函數設計中,在求解偏微分方程的相關正問題和反問題方面獲得了很好的效果.PINN 方法的基本框架理念是由Lagaris 等[14]在20 世紀90 年代提出的,而Raissi 等[13]結合深度學習技術(如自動微分)實現并擴展了應用場景.

PINN 方法在流體動力學[15-19]、熱傳導[20-21]、地球物理學[22-25]、固體力學[26-29]、生物醫學[30]等多個領域中獲得了應用(表1).綜述文獻[31-34] 對PINN 方法及其應用作了較為詳細的介紹.

表1 PINN 方法在不同領域中的應用Table 1 Application of PINN method in different fields

已有少數研究者將物理信息神經網絡方法應用于波動方程的求解以及全波形反演.比如Moseley等[23]設計了一個物理信息神經網絡求解復雜二維聲學介質中的壓力響應,該網絡只使用解的前幾個時間步作為訓練數據,可模擬分層介質、Marmousi p 波速度模型中由波動方程引起的各種物理現象.Rao 等[28]提出一種不依賴于任何標記數據的物理信息神經網絡來建模彈性動力學問題,成功對彈性波在有限域中的傳播進行了模擬.Rasht-Behesht等[24]提出了適用于二維聲波波動方程的PINN算法,通過將傳感器數據加入網絡進行訓練,可在前向求解的同時實現全波形反演(FWI).在前人工作的基礎上,本文提出了一種基于物理信息神經網絡的近場波動模擬方法,探索了遷移學習在波動問題中的應用以及復雜起伏地表邊界在PINN 中的實現方法.

本文從物理信息深度學習的數學理論出發,系統探討該方法應用于近場波動數值模擬的相關問題,包括模型及損失函數構建以及優化器模式等.通過多組數值試驗對所提方法應用于均質場地、空間不均勻及復雜地形場地時的有效性進行驗證.

1 動力系統物理驅動深度學習原理

通過對時空偏微分方程的初、邊值問題來解析物理驅動深度學習方法的設計原理.設u(x,t)滿足如下形式的偏微分方程

式 中,u(x,t) 為偏 微分方法 的解,D (·) 為帶參數 λ的微分算子,x是域? ∈Rd(d=1,2,···,n)中的空間變量,域邊界 ? ?由Dirichlet 邊界 ? ?D和Neumann 邊界 ? ?N組成.t∈[0,T]為 時間變量.BD(t),BN(t),I0(x),I1(x)分別代表偏微分方程初邊值問題中的Dirichlet和Neumann 邊界條件以及初始條件函數.

眾多動力系統均可采用上述形式來建模.通過給定物理模型的初始條件 I0(x),I1(x)和邊界條件BD(t),BN(t),采用解析或數值方法求解偏微分方程得到任意時、空點的解值量u(x,t).從函數逼近論的角度,具有單一隱藏層的神經網絡可精確逼近任何線性/非線性連續函數或運算符[35],因此可以將神經網絡看作非線性函數逼近器.Raissi 等[13]考慮通過訓練全連接神經網絡 N N(x,t;θ)來逼近偏微分方程的解,其中 θ表示網絡中的可訓練參數.深度學習現已實現強形式的自動微分技術,并集成在包括Pytorch 及Tensorflow 等開發平臺中,并獲取神經網絡所逼近的方程解的各階偏導數,實現將PDE 以及初、邊值殘差作為正則項加入損失函數中.

對于上述的時空偏微分初、邊值問題,通過設計如下損失函數 L (θ)來架構并訓練神經網絡

式中,Lp(θ),Lbc(θ),Lic(θ)分別為PDE 殘差損失項、邊界條件損失項和初始條件損失項.在全域 ?,Dirichlet邊界 ? ?D和Neumann 邊界 ? ?N選取的時空采樣點個數分別為Np,Nd,Nn,其中時間t∈[0,T].參與計算初始條件損失項的時空采樣點個數為Nic.使神經網絡逼近的解收斂到偏微分方程真解,需選擇足夠數量的時空采樣點,本文采用Sobol 序列算法[36]進行時空采樣.

以無源項一維波動(一維波動方程)為例,介紹物理驅動深度學習的實現方法.

初始條件

邊界條件

式中,波速c=1.上述波動方程解析解為

使用Sobol 序列算法分別生成PDE 殘差損失項、初始條件損失項、邊界條件損失項的時空采樣點,Np=5000,Nd=400,Nn=400,采樣點的空間分布如圖1 所示.采用3 個隱藏層、每層100 個神經元的全連接神經網絡.定義PINN 的預測結果與解析解之間的相對 L2范數誤差為

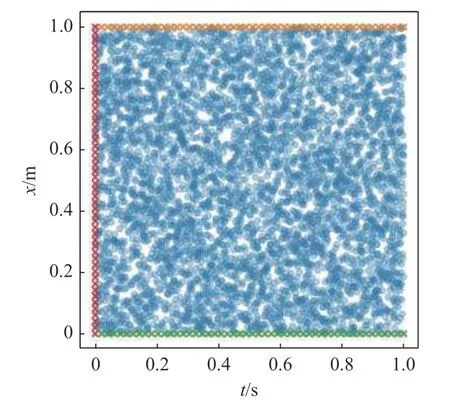
圖1 無源項一維波動問題: 不同損失項采樣點時空分布Fig.1 One-dimensional fluctuation problem of passive term:spatiotemporal distribution of sampling points for different loss terms

使用Adam 優化器訓練40000 步,各個損失項以及相對誤差收斂過程如圖2 所示.PINN 的預測解與解析解、有限差分方法計算的數值解對比如圖3所示.其中,有限差分方法中空間、時間離散均采用標準的二階中心差分格式,網格大小分別為0.01 m和0.005 s.PINN 的預測解、有限差分解與解析解之間的絕對誤差最大值分別為0.008 m 和0.007 m.圖3表明: 經過訓練的神經網絡已具備較強逼近波動方程真解的能力.

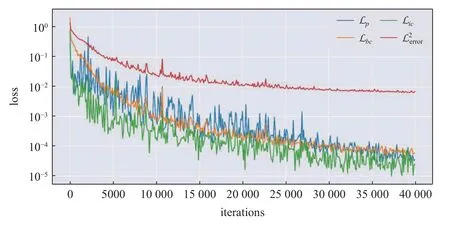
圖2 無源項一維波動問題: 神經網絡訓練過程中不同損失項的演化Fig.2 One-dimensional fluctuation problem of passive terms: evolution of different loss terms during neural network training

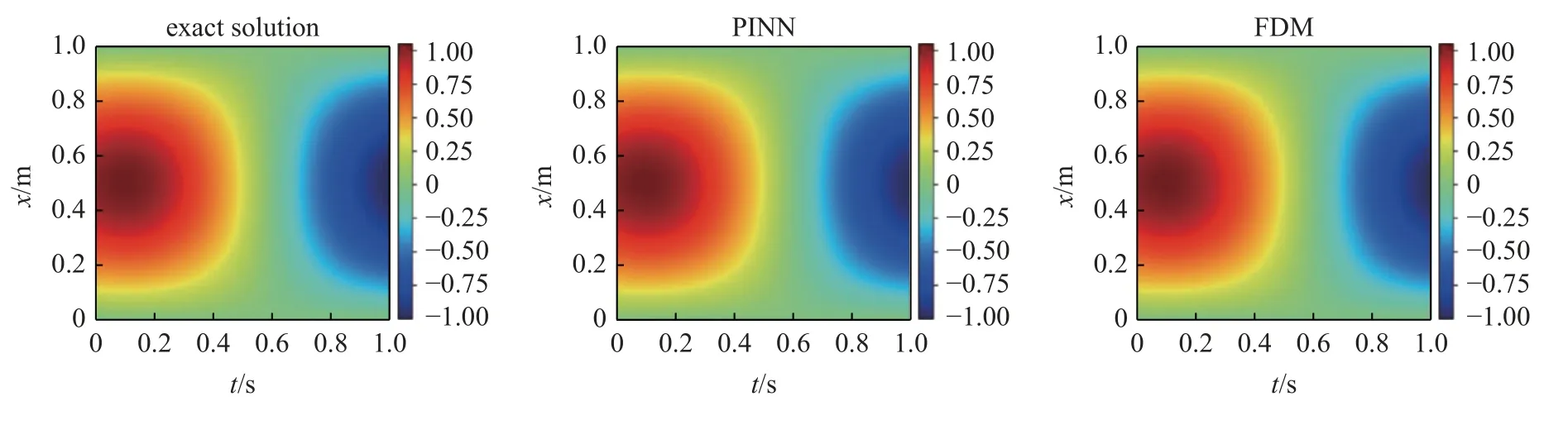
圖3 無源項一維波動問題: 解析解與PINN 預測的結果對比Fig.3 One-dimensional fluctuation problem with passive term: comparison between analytical solution and PINN prediction

2 物理信息深度學習波動數值模擬

2.1 方法介紹

以二維波動問題闡明物理驅動深度學習方法求解波動方程的實現過程.二維標量波方程為

式中,u(x,z,t) 為出平面波動位移,c為介質物理波速.f(x,z,t) 為外荷載,令f≡0,并通過給定初始波場等效施加外力.

在求解二維波動方程的PINN 框架中,指定網絡的輸入為時空坐標X=(x,z,t),輸出為神經網絡逼近的PDE 解,即位移場Y=u(x,z,t).采用深度學習自動微分方法,計算得到,并構建損失函數.本文采用譜元法計算得到的t1,t2時刻的兩個早期位移場作為初始條件,第一個波場快照 U1約束了震源的位置和形狀,第二個波場快照 U2約束波動傳播方向.垂直地表的應力為零的邊界條件可通過損失函數中的Neumann 邊界條件 ?u(x,z=zmax,t)=0表示.包含PDE 殘差損失項 Lp(θ)、初始條件損失項 Lic(θ)、自由邊界條件損失項 Lbc(θ)的損失函數L(θ)可表示為

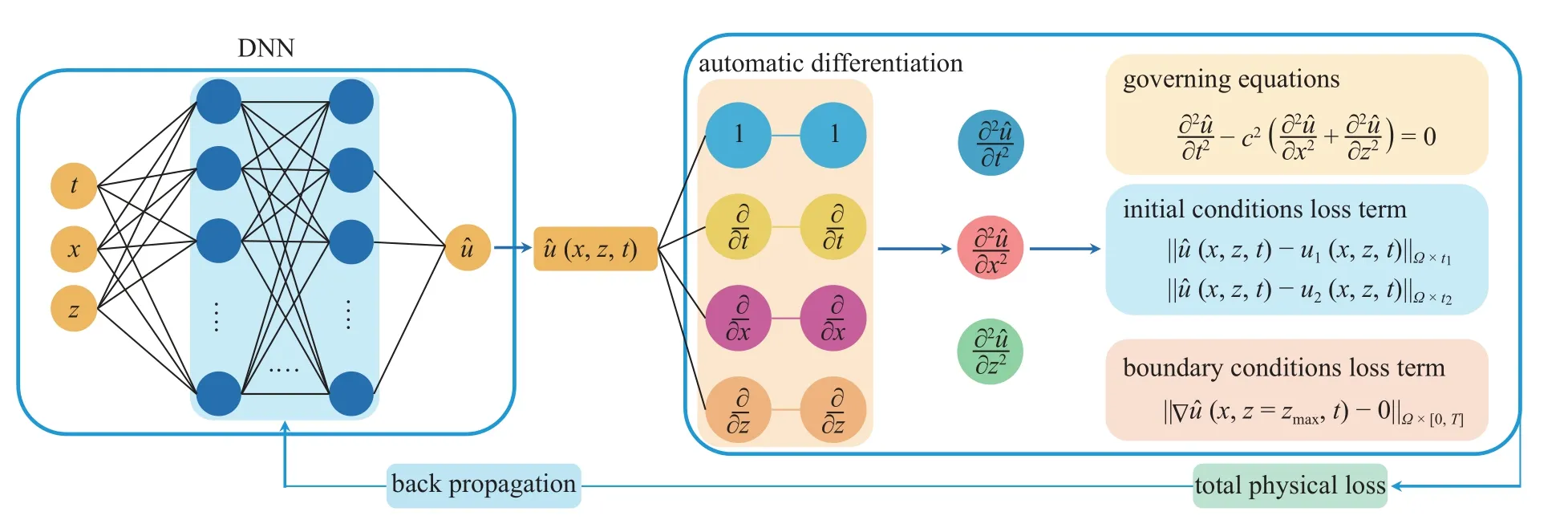
圖4 求解二維波動方程的物理信息神經網絡架構圖Fig.4 Physical information neural network architecture diagram for solving the 2 D wave equation

2.2 方法驗證

以無限均勻介質中的內源波動問題為例,驗證方法的可行性.計算模型如圖5 所示,模型所在區域為寬600 m、高600 m 的矩形,介質物理波速c=400 m/s.

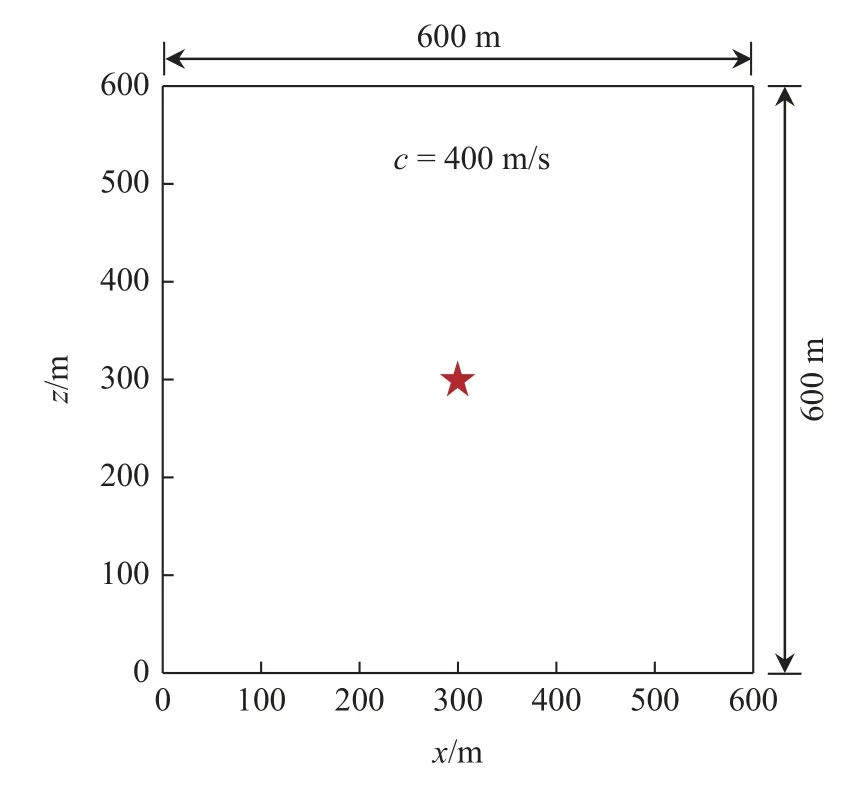
圖5 無限均勻介質內源波動計算模型Fig.5 Calculation model of endogenous fluctuation in infinite uniform medium

使用譜元方法計算得到t1=0.18 s,t2=0.2 s 的位移場作為初始條件參與訓練,其余時刻的結果作為真解對PINN 的計算結果進行精度對比.譜元法中使用二階顯式Newmark 時間步長格式,時間步長為0.1 ms,計算總時長為0.9 s.PINN 中的波場時刻從第一個初始條件的時間t1=0.18 s 算起,波場訓練的最終時刻為T=0.72s.采用四階勒讓德譜單元對模型在 1 00×100的網格上進行空間離散.PINN 方法具備稀疏數據下的高精度學習能力,僅使用兩個時刻的50 × 50 的波場作為初始條件進行訓練,即可達到與譜元方法相關系數超過0.99 的精度.

在模型四邊各5 個單元厚度的區域邊界使用完美匹配層[37](PML)以模擬點源在無限介質中的傳播.輸入波位移時程采用主頻為20 Hz 的高斯源時間函數,源位置處于模型中心x=300m,z=300m.采用Sobol 序列算法在整個域中生成用于計算PDE殘差損失項的采樣點和初始條件采樣點,空間分布如圖6 所示.采樣點數Np=10 000,Nic1=2500,Nic2=2500.

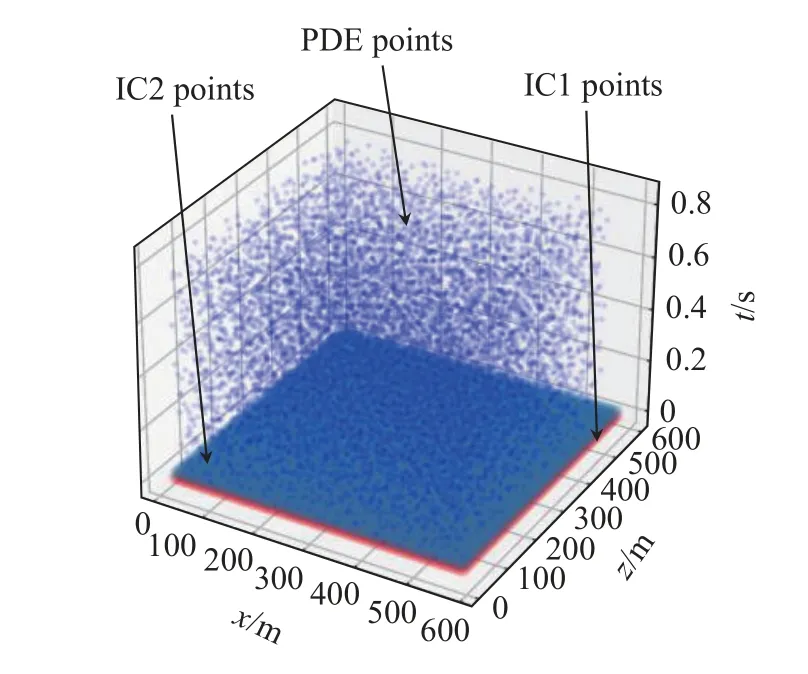
圖6 無限均勻介質波動問題不同損失項時空采樣點分布Fig.6 Spatio-temporal sampling points distribution of different loss terms for infinite uniform medium fluctuation problem

使用5 個隱藏層,每層30 個神經元的全連接網絡逼近公式(7)的解.使用學習率為6×10?3的Adam優化器和L-BFGS 優化器分別訓練10000 步.優化組合增強了PINN 的全局搜索和局部調優能力,從而得到高精度的結果.模型訓練后,可對任意分辨率下任意時空點的波動方程解及解的各階偏導進行預測.定義某一時刻PINN 方法與譜元方法模擬波場之間的決定系數R2為

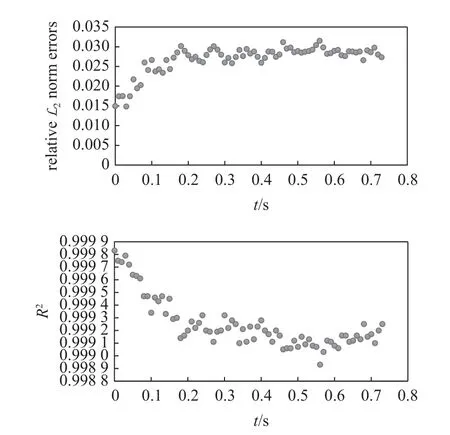
圖7 PINN 方法與譜元方法模擬波場之間的相對 L2 范數誤差與決定系數 R2Fig.7 Relative L2 norm error and determination coefficient R2 between the results of PINN method and spectral element method

圖8 表明: PINN 方法對波場的預測結果與譜元的結果基本一致,可以準確捕捉到波動在無限介質中的傳播特性.訓練中并未對邊界施加任何約束,內域的波動也可實現邊界透射.

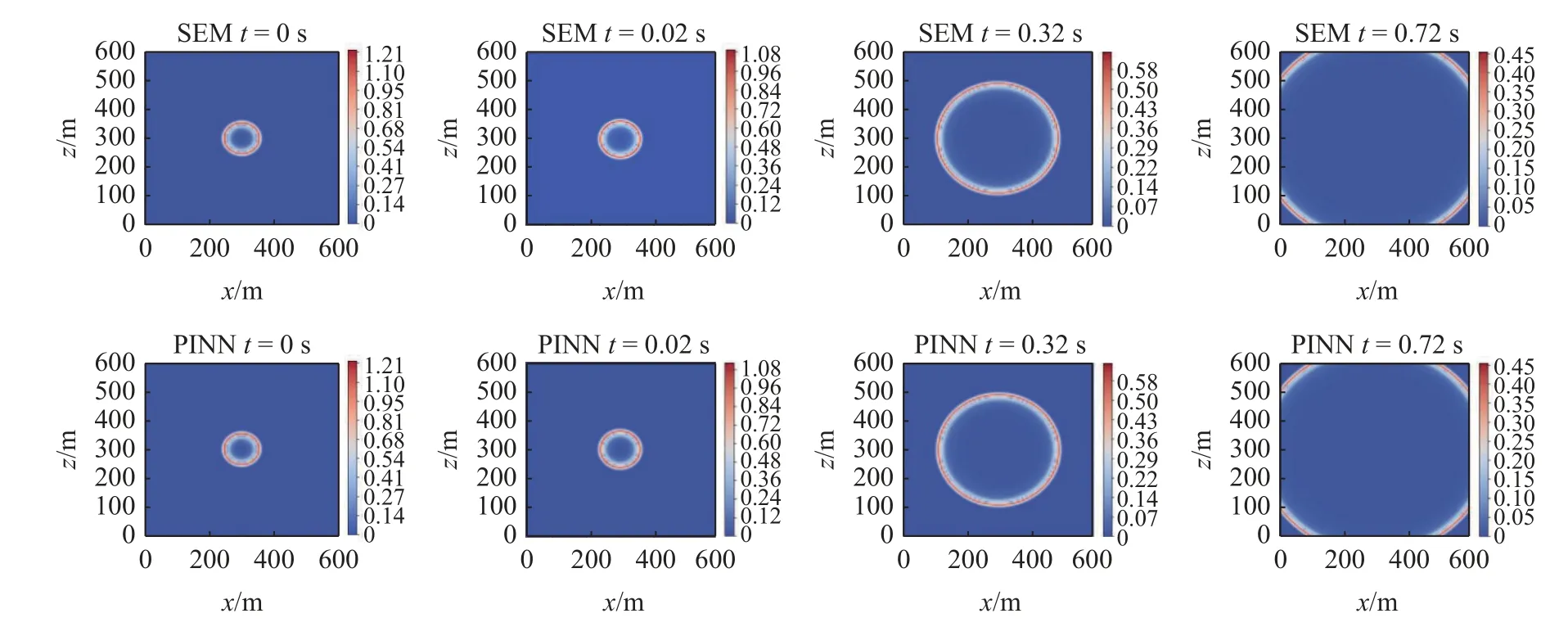
圖8 無限均勻介質波動問題: 譜元法與PINN 模擬的波場快照對比Fig.8 Wave field snapshot of spectral element method and PINN simulation

構建不同初始條件進行測試,發現經過訓練的神經網絡具有在不同初始條件下進行泛化的能力.僅改變上例中的源位置為x=200m,z=200m,使用譜元法生成t=0.18 s,t=0.2s 的位移場作為新的初始條件輸入網絡參與構成損失函數.在源位置為x=300m,z=300m 訓練的神經網絡可直接對新的初始條件進行泛化,得到高精度預測結果.PINN 方法與譜元方法模擬波場之間的相對 L2范數誤差以及決定系數R2如圖9 所示.圖10 給出了其中四個時刻模擬波場對比,圖中的時間均為與第一個初始條件相隔的時間.

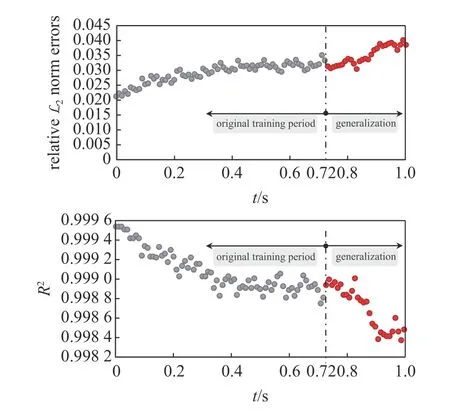
圖9 PINN 方法使用遷移學習與譜元法模擬波場之間的相對 L2 范數誤差與決定系數 R2Fig.9 Relative L2 norm error and determination coefficient R2 between the results of PINN method using transfer learning and spectral element method

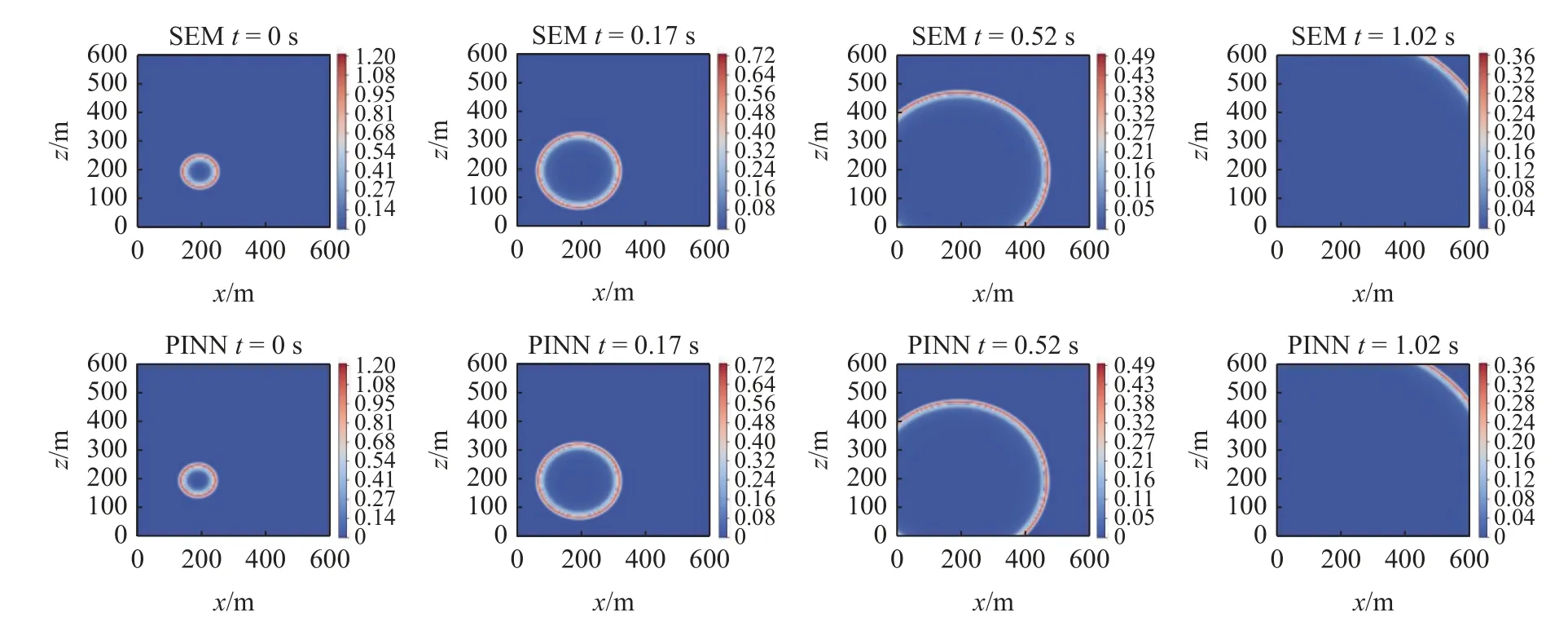
圖10 譜元法與PINN 方法使用遷移學習得到的波場快照對比Fig.10 Wave field snapshots obtained using spectral element method and PINN method using transfer learning

由圖9 可知,超出訓練時間范圍后,相對 L2范數誤差出現較快的上升段、決定系數R2出現較快的下降段.在t=1.02 s 波即將完全透出的時刻,仍與譜元方法保持0.99 以上的高相關性,由此可見波場訓練最終時刻為0.72 s 的物理驅動神經網絡具有在新的初始條件下進行一定時間外推的能力.模擬結果驗證了遷移學習在近場波動問題中應用的可行性.

3 物理驅動深度學習波動模擬應用

3.1 空間不均勻介質波動模擬

為進一步驗證PINN 方法處理復雜介質波場問題的有效性,考慮空間不均勻介質中二維波動問題.模型所在區域為寬1000 m、高1000 m 的矩形,在波速c=1000m/s 的基礎上,添加四個二維高斯混合的復雜波速分布.計算模型及介質物理波速分布如圖11 所示,波速分布范圍為500 m/s～ 1000 m/s.

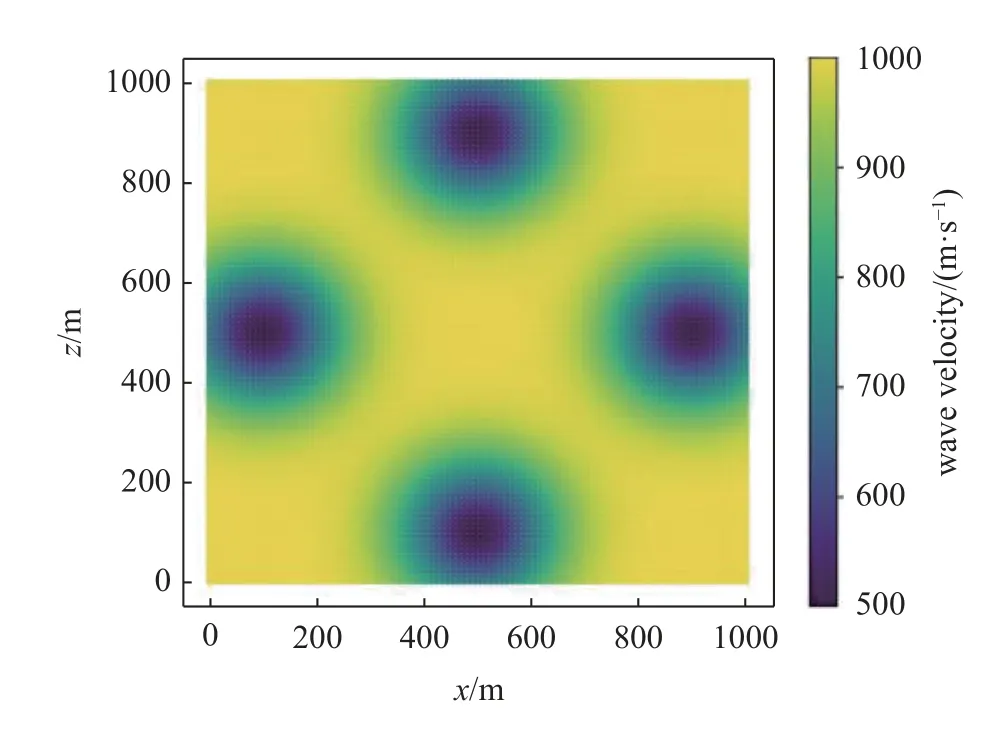
圖11 空間不均勻介質物理波速分布Fig.11 Physical wave velocity distribution in spatially inhomogeneous media

使用譜元方法計算t=0.15 s,t=0.175s 的位移場作為初始條件參與訓練,其余時刻的結果與PINN 方法結果進行對比.每個初始條件的采樣點為50×50共2500 個采樣點.譜元法中二階顯式Newmark時間步長格式的時間步長為0 μs,計算總時長為0.7 s.PINN 中的計算時間從第一個初始條件的時間t1=0.15s 算 起,訓練波 場的最 終時刻 為T=0.55s.

訓練由兩部分構成,首先使用學習率為6×10?4的Adam 優化器訓練10000 個epoch,實現全域收斂,再調用L-BFGS 優化器實現優化收斂,訓練步數為40000 步.

PINN 方法與譜元方法模擬波場之間的相對 L2范數誤差以及決定系數R2如圖12 所示.圖13 對比了不同時刻PINN 預測和譜元方法模擬的結果,圖中的時間為與第一個初始條件相隔的時間.結果表明: PINN 方法可實現非均勻介質中的高精度波動模擬.

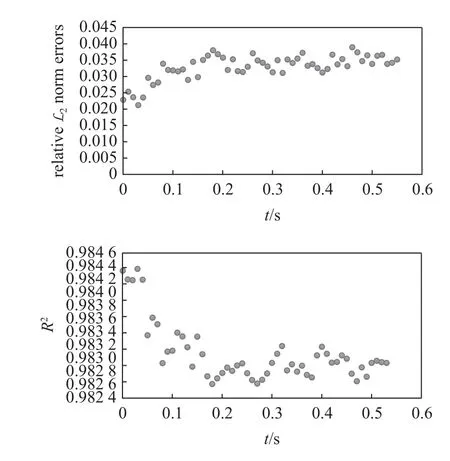
圖12 PINN 方法與譜元方法模擬波場之間的相對 L2 范數誤差與決定系數 R2Fig.12 Relative L2 norm error and determination coefficient R2 between the results of PINN method and spectral element method

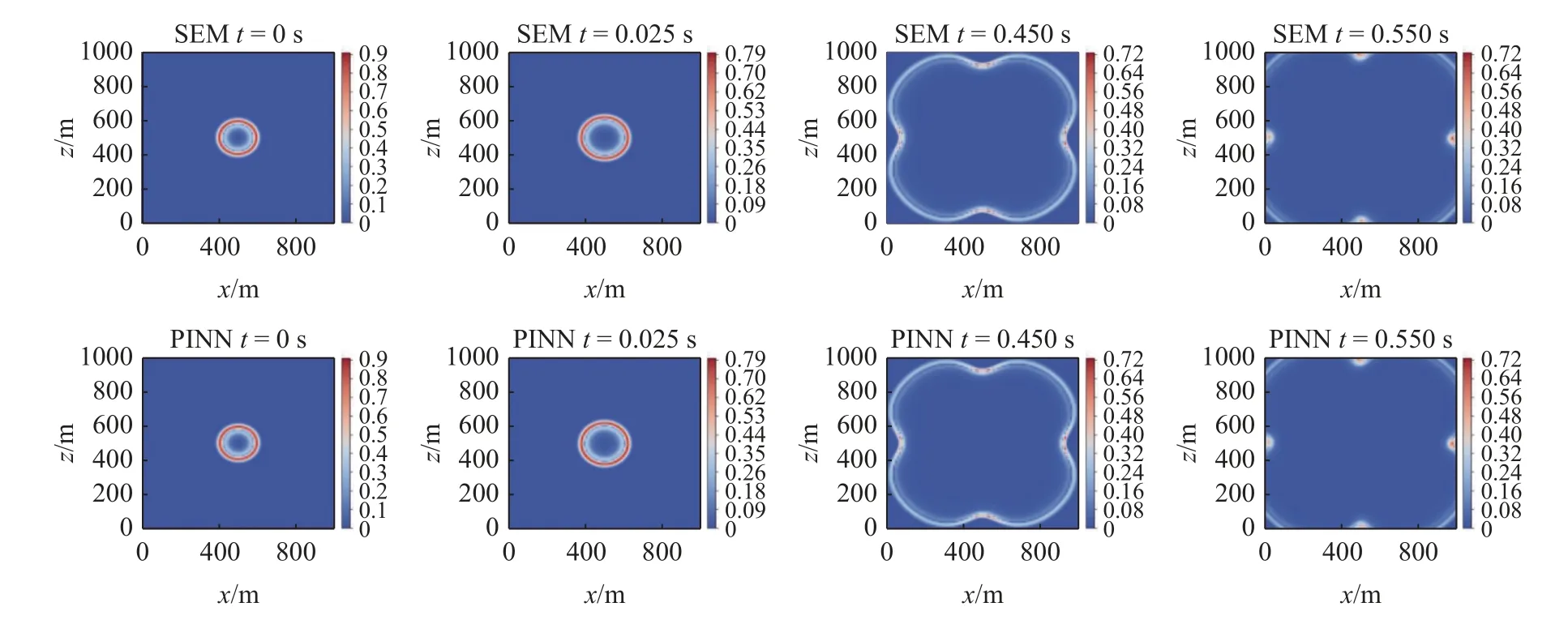
圖13 空間不均勻介質波動問題: 譜元法與PINN 模擬的波場快照Fig.13 Spatially inhomogeneous media fluctuation problem: wave field snapshots simulated by spectral element method and PINN

3.2 起伏地形波動模擬

物理驅動神經網絡實現波動模擬的一個關鍵問題是自由邊界條件的加載方法.自由地表條件理論上概念明確,有限元法、譜元法可自動滿足,地表起伏增加了求解與建模的難度[38].本文采用PINN 方法開展相關工況驗證.

構建左邊界長度為450 m、底邊界長度為1200 m計算模型,介質物理波速c=1000 m/s,如圖14 所示.

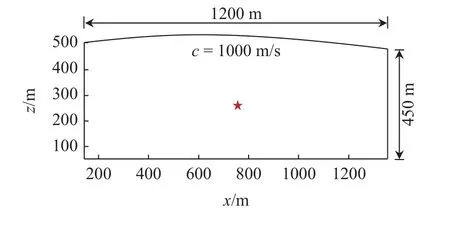
圖14 起伏地形內源波動問題計算模型Fig.14 Computational model for endogenous fluctuation problems in undulating terrain

使用譜元方法分別計算了無限介質中t=0.09s,t=0.1 s 的位移場作為初始條件、起伏地表下t=0.3s內的位移場作為精度驗證.兩種計算模型均采用四階勒讓德譜單元在 1 00×100的網格上進行空間離散,其中每個初始條件使用 5 0×50共2500 個采樣點.吸收邊界仍使用5 個單元厚度的完美匹配層(PML).輸入波位移時程采用主頻為20 Hz 的高斯源時間函數,源位置為x=250 m,z=750m.采用Sobol 序列算法在整個域中生成用于計算PDE 殘差損失項和自由邊界條件損失項的采樣點,采樣點數分別為Np=10 000,Nbc=2500.采樣點的空間分布如圖15 所示.

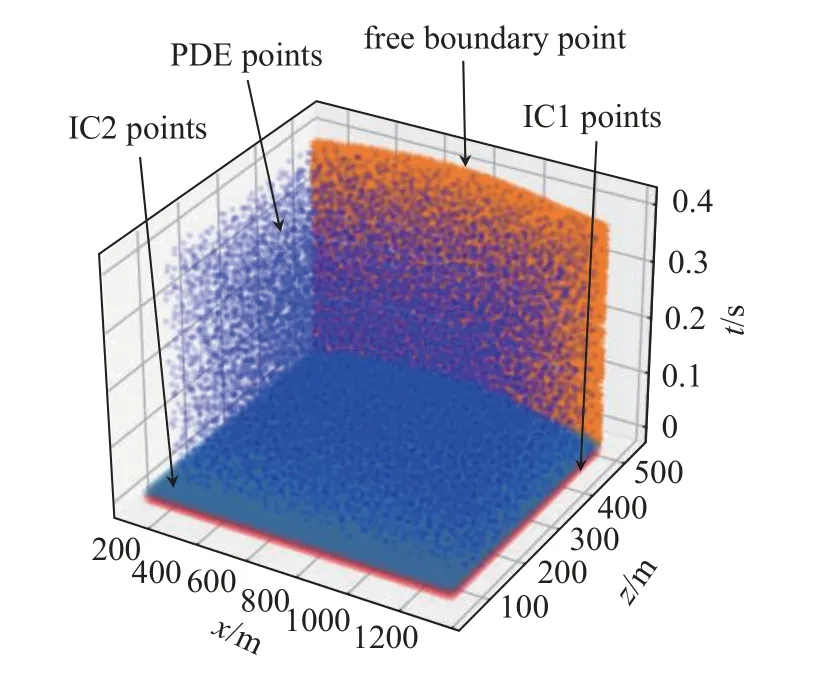
圖15 起伏地形內源波動問題不同損失項時空采樣點分布Fig.15 Distribution of spatial and temporal sampling points for different loss terms for endogenous fluctuation problems

使用5 個隱藏層,每層30 個神經元的全連接網絡.調用學習率為6×10?3的Adam 優化器訓練10000個epoch,再使用L-BFGS 優化器訓練40000 步.PINN 方法與譜元方法模擬波場之間的相對 L2范數誤差以及決定系數R2如圖16 所示.圖17 展示了三個時刻的PINN 預測和譜元方法模擬結果對比,圖中的時間為與第一個初始條件相隔的時間.

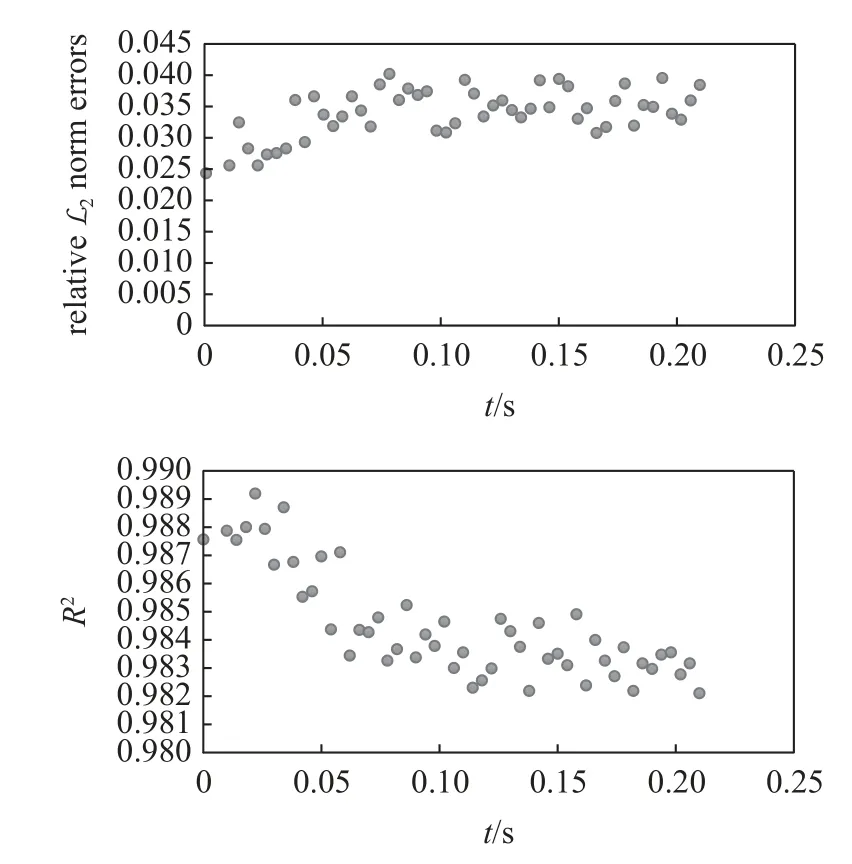
圖16 PINN 方法與譜元方法模擬波場之間的相對 L2 范數誤差與決定系數 R2Fig.16 Relative L2 norm error and determination coefficient R2 between the results of PINN method and spectral element method

圖17 起伏地表內源波動問題: 譜元法與PINN 模擬的波場快照Fig.17 Internal fluctuation problem of undulating surface: wave field snapshots of spectral element method and PINN simulation

4 結論與展望

本文結合波動數值模擬基本理論與物理驅動深度學習,建立了包括一維無源、二維波動模擬方法.通過與理論解、譜元計算結果等對比,驗證了方法應用于均質場地、空間不均勻及復雜地形場地的有效性.得到的主要結論與展望如下.

(1) 物理驅動深度學習PINN 方法可實現波動模擬,并可結合稀疏初始波場數據,實現高精度泛化.方法具備無網格、精細化,波場透射等優勢.物理驅動神經網絡僅需存儲網絡參數,對硬件存儲要求較低.

(2) 針對典型工況,訓練形成的神經網絡具有在不同初始條件的泛化能力,結合遷移學習,可顯著提高網絡的訓練效率.

(3) 通過“軟約束”可在PINN 方法中嵌入應力型及位移型等不同邊界條件.由于物理驅動深度學習計算損失函數的靈活性,可展望PINN 方法與有限差分、偽譜法等多類型數值算法開展耦合,以實現對空間大尺度、高精度復雜波動問題的模擬.