重復折疊后SMPC可展桁架陣面天線模態試驗與分析

王曉情，楊天洋，張祎貝，高冀峰，陳務軍，房光強，謝 超，曹爭利，馬 嘉

(1. 上海交通大學 空間結構研究中心，上海 200240； 2. 上海宇航系統工程研究所，上海 201108)

隨著航天技術的發展和革新，智能材料和結構作為前沿研究熱點拓展了大型空間可展桁架的應用形式，其中熱致形狀記憶復合材料(shape memory polymer composite, SMPC)因激勵形式簡單，可恢復應變大等優勢得到廣泛關注，它在外界環境溫度激勵下，可實現“記憶起始態→固定變形態→恢復起始態”的變形循環，具有特定的感知和響應能力，由SMPC縱梁作為主要支承構件的三棱柱可展桁架陣面天線便利用了桿件的熱致形狀記憶的效應實現折疊和展開[1]。

SMPC可展桁架陣面天線整體尺度大，動力學固有特性將表現出頻率低、阻尼小以及模態密集的動力學特征。此外，其工作所處空間環境復雜，容易受到因空間環境熱輻射或電機驅動導致的振動影響[2]，產生不易衰減的振動響應。為方便進行振動控制，許多研究人員對可展桁架天線結構進行了動態特性分析。張祎貝等[3]對織物復合材料空間可展桁架進行模態分析，探究了懸掛系統和斜加勁索剛度對結構模態的影響。劉梅等[4]建立了大型空間柔性正三棱柱桁架結構的等效梁模型，通過動力學分析比較了桁架結構和等效梁模型的固有特性，驗證了該模型具有較高精度。陳子杰[5]設計了一種三棱柱式可展開平面天線機構，對機構的展開態進行了計算模態分析和結構參數優化。

SMPC可展桁架須在地面進行各種折疊展開形狀記憶重復試驗以及系統功能、性能試驗后，再發射入軌，因此，歷經重復折疊后SMPC桁架性能的試驗是關鍵問題。SMPC的熱致形狀記憶效應決定了其材料性能容易受到溫度等環境因素的影響[6-7]，且其經歷重復折疊展開后，材料發生漸進損傷將導致構件剛度發生改變[8-9]。目前尚無經歷重復折疊后的SMPC可展桁架動力特性研究，為建立準確有效的動力學特性分析方法，有必要在構件層面對SMPC的彈性屬性進行校核。同時，SMPC可展桁架陣面天線的主要組成構件有陣面板和預應力索，而它們對整體結構動力學特性的影響目前少見研究報道，為探究其組成構件對動力特性的影響，為后續結構優化設計和振動控制提供設計依據，以經歷重復折疊展開形狀記憶歷程后的五節SMPC可展桁架陣面天線為研究對象，開展了自由狀態下地面模態試驗，分析陣面板和預應力索對桁架結構模態參數的影響，建立了考慮空氣阻力效應的有限元模型，進行數值模擬并與試驗結果對比分析。

1 SMPC可展桁架陣面天線

1.1 組 成

SMPC可展桁架天線為三棱柱構型，主要由重復折疊展開后的SMPC縱梁、三角形隔件、斜向預應力索和通過鉸鏈連接的陣面板構成，如圖1所示。五節桁架天線的基本框架由SMPC縱梁以及三角形隔件組合而成，連接方式采用標準節段的端法蘭對接后螺栓緊固，在此基礎上考慮預應力索和陣面板對桁架天線動力學特性的影響，根據組成定義四個工況：工況1為“五節桁架”；工況2為“工況1+預應力索”；工況3為“工況1+陣面板”；工況4為“工況1+預應力索+陣面板”，各工況示意圖如圖2所示。

圖1 SMPC桁架陣面天線示意圖Fig.1 Schematic diagram of the SMPC truss array antenna

圖2 各工況組成示意圖Fig.2 Schematic diagram of working conditions

1.2 SMPC縱梁參數

五節可展桁架陣面天線共包含了15根SMPC縱梁，截面為薄壁圓管?100×1，長度2 770 mm。為測得重復折疊展開后SMPC梁的剛度，同時避免構件發生損壞，通過動態法測量其彈性模量[10]。

1.2.1 SMPC縱梁模態試驗方案

采用激光測振技術測量自由狀態下的SMPC梁的振動特性，通過兩根彈性橡皮繩懸掛SMPC梁模擬自由邊界，為避免邊界對自由狀態振動特性的影響，橡皮繩的彈性剛度應保證足夠低，其自振頻率應遠離關心的頻率范圍。沿著SMPC梁縱向均勻布置反光靶點，激振器分別設置在縱梁的端部和中間進行激振，以充分激發出自由狀態下的各階振型，現場布置如圖3所示。

圖3 SMPC縱梁模態試驗布置圖Fig.3 Modal test layout of SMPC longitudinal beam

1.2.2 SMPC縱梁模態試驗結果與分析

典型的模態試驗結果如圖4所示，其中呼吸模態表現為圓管徑向的起伏變形，從頻響曲線可知一階彎曲振型參與度最大，一階頻率平均值為58.1 Hz。建立有限元模型定量探究楊氏模量和剪切模量對一階固有頻率的影響，單元類型選用梁單元(B31)，采用Lanczos求解器求解特征值，并利用Isight參數化設計得到“一階固有頻率-彈性模量-剪切模量”的關系(如圖5所示)，采用多項式擬合曲線，將與試驗結果最吻合的彈性參數作為SMPC可展桁架各縱梁的平均材料屬性。

圖4 SMPC梁自由狀態模態試驗頻響曲線及振型圖Fig.4 Frequency response curves and modal shapes of modal test of SMPC beam in free state

圖5 SMPC梁一階固有頻率-楊氏模量-剪切模量關系圖Fig.5 The first-order natural frequency versus Young’s modulus and shear modulus of the SMPC beam

1.3 幾何及材料參數

三角形隔件由兩層互補對偶隔件疊加而成(如圖6所示)，隔件桿截面為矩形泡沫填充管50×10×3×2，預應力通過?1.8 Kevlar索施加。陣面板由外框架及模擬陣面(4 mm KT蒙皮)組成，如圖7所示。假設各構件屬性為線彈性，SMPC縱梁剪切模量1.5 GPa，其余構件泊松比0.3，幾何與材料參數如表1所示。

圖6 三角形隔件示意圖Fig.6 Schematic diagram of the triangular spacer

圖7 陣面板示意圖Fig.7 Schematic diagram of the array panel

表1 各構件幾何與材料參數Tab.1 Geometry and material parameters of each component

2 模態試驗與分析

2.1 試驗方法

試驗通過固定式懸掛系統補償桁架天線的重力，以模擬微重力環境，采用柔性橡皮吊繩分別懸掛桁架和陣面板以模擬自由狀態。采用多點輸入多點輸出的信號采集方式，同時設置兩個激振器進行隨機激振，激振位置分別位于桁架縱向的兩端，避開結構振型的節點位置。桁架上布置三向加速度傳感器，以研究桁架整體的模態振型，如圖8所示。模態測試分析系統采用LMS Testlab分析平臺中的Modal Analysis模塊，采用最小二乘復頻域法進行模態參數識別，配合模態確信指標MAC驗證振型的正交性

(1)

式中，{U}和{V}為兩個模態的振型向量，對于不同階次模態的兩個振型向量，MAC值應接近于0；對于同階次模態的振型向量，MAC值應接近于1。

圖8 傳感器及激振位置Fig.8 The sensor and excitation position

2.2 試驗結果與分析

忽略試驗結果中剛體運動模態，各工況的模態參數結果統計如表2所示(“Y向彎曲”指彎曲所在平面法向為Y方向)，注意到工況3的模態試驗結果中激振器未激勵出Y向彎曲的振型，各階振型示意圖如圖9所示。

由表2可知，各工況下第一階模態均為扭轉模態，說明結構的扭轉剛度較彎曲剛度低。無預應力索的工況均出現了縱向錯動振型，而有預應力索的工況未出現，說明預應力的施加有利于提高結構沿縱向的抗剪剛度，限制結構沿Z方向的錯動變形。

表2 模態參數識別結果Tab.2 Identification results of modal parameters

圖9 SMPC桁架振型示意圖Fig.9 Schematic diagram of the SMPC truss modal shape

圖10和圖11提供了各工況典型振型的頻率對比，無陣面板的工況下，施加預應力后一階扭轉頻率提高了12.4%，Y向一階彎曲頻率提高了287%，Y向二階彎曲頻率提高了186%，Y向三階彎曲頻率提高了115%。而有陣面板的工況下，預應力的施加可提高一階扭轉頻率95.9%。單獨考慮預應力索或陣面板的工況對于結構整體的二階扭轉貢獻不大，而同時考慮陣面板和預應力索的工況可提高二階扭轉頻率75.5%，故可知預應力的施加可提高結構的整體剛度。

圖10 自振頻率-模態振型關系圖Fig.10 Natural frequency versus modal shape

陣面板對扭轉和彎曲模態均有質量貢獻，特別的，在施加預應力的工況下陣面板還提供了扭轉剛度上的貢獻。無預應力索的工況下，陣面板沒有提高結構的扭轉頻率。而有預應力索的工況下，陣面板可使一階扭轉頻率提高了68.9%，二階扭轉頻率提高了76.0%，說明陣面板對結構的扭轉剛度貢獻需要在預應力存在的前提下才能發揮，此外，陣面板使得結構的一階至三階彎曲頻率分別降低了28.0%，35.1%和42.3%，說明陣面板對Y向彎曲模態的貢獻主要體現在增加桁架的整體質量，原因是陣面板與桁架通過鉸鏈連接，而鉸鏈存在一定的Y向轉動自由度，導致陣面板對結構Y向彎曲的剛度貢獻小。

圖11 自振頻率-試驗工況關系圖Fig.11 Natural frequency versus working condition

3 模態分析

3.1 有限元模型

圖2為針對四種工況在ABAQUS 2021建立的有限元模型，SMPC梁、隔件和陣面板框架采用兩節點線性梁單元(B31)進行建模，陣面采用四節點減縮積分通用殼單元(S4R)，預應力索單元類型設為梁單元(B31)，并在材料屬性中設為只能承受拉力，鉸鏈采用“MPC: beam + Hinge +MPC: beam”約束方式，如圖12所示。

圖12 鉸鏈約束Fig.12 Hinge constraint

有陣面板的工況中，由于模擬陣面密度輕，表面積大，結構動力學固有特性受空氣的影響不容忽略[11]，故在模型中考慮空氣和結構的聲固耦合(acoustic structure interaction, ASI)作用，計算結構的濕模態。考慮空氣流體影響的數值方法包括有限元，邊界元和無限元等方法，本文采用更具適用性的有限元法，假設空氣流體是無黏可壓縮的，則聲固耦合系統的無阻尼自由振動方程[12]

(2)

式中：u為結構的節點位移矢量；p為流體的節點動壓力矢量；K和M為結構的剛度和質量矩陣;H和Q為流體的“剛度”和“質量”矩陣;L為流固界面耦合矩陣;ρ為流體密度。

求解式(2)的特征值問題即可確定考慮聲固耦合作用的結構頻率和模態。室溫下空氣密度設為1.17 kg/m3，體積模量0.14 MPa，以結構的中心為圓點建立直徑30 m的球形空氣域，單元類型為AC3D10單元，球體外表面設為無放射邊界條件。陣面板框架與陣面設置綁定約束，在計算模態時為考慮空氣-陣面的聲固耦合作用，空氣域與陣面進行綁定約束，ASI模型如圖13所示。

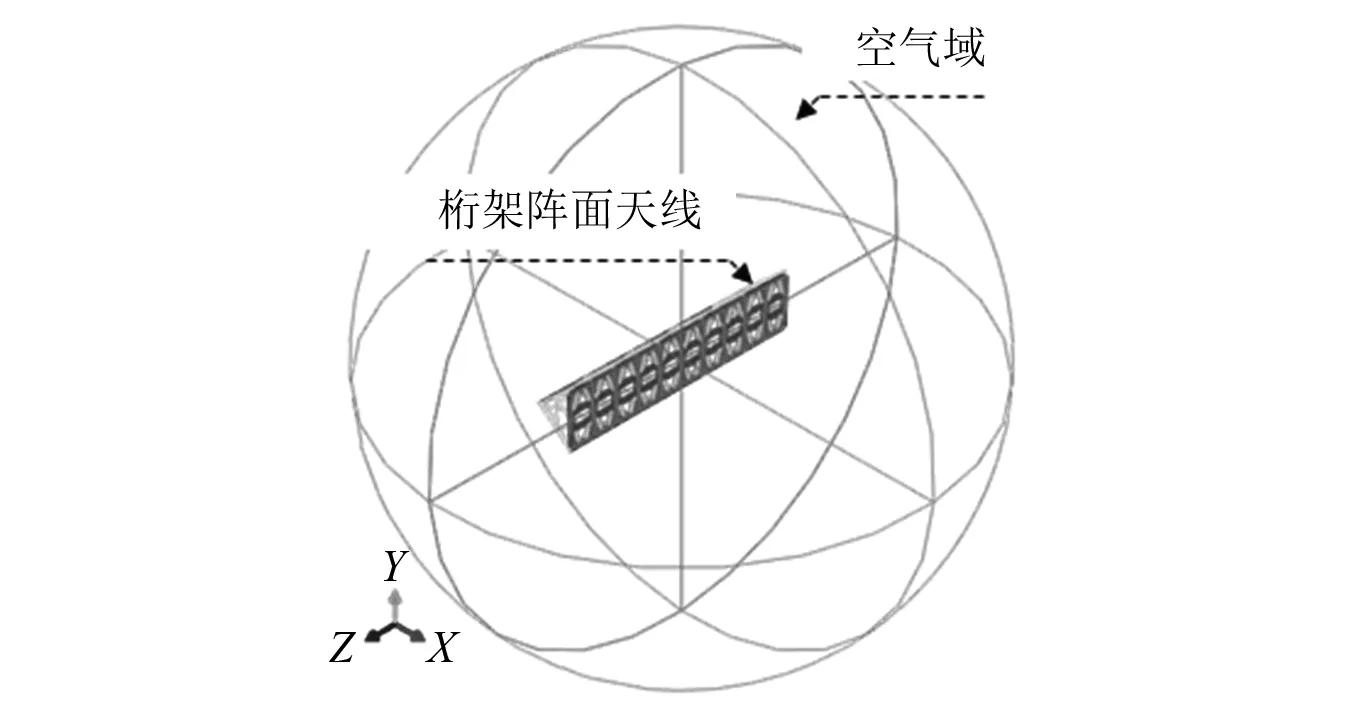
圖13 聲固耦合模型Fig.13 Acoustic structure interaction model

對于有預應力索的工況，應分兩步，分別為靜力分析和模態分析。考慮到預應力的大小對結構線性模態的影響較小[13]，預應力的施加采用實測平均水平，在初始分析步中對預應力索施加100 N的預拉力，考慮幾何非線性。為模擬結構試驗中的自由邊界條件，靜力分析步不設置任何位移約束條件。頻率分析步中采用Lanczos求解器計算模態。對于無預應力索的工況，僅考慮頻率分析步。

3.2 仿真結果與對比分析

不考慮剛體運動模態，仿真結果中出現了三角形隔件或陣面的局部模態振型，由于模態試驗中未在陣面及隔件上布置傳感器，因此無法得到該局部振型。以試驗結果中的模態階次為參照，忽略仿真出現的局部振型，表3比較了各工況下桁架的模態結果，可知各工況仿真和試驗的結果較為吻合，誤差在20%以內，分析誤差的原因包括：①仿真中桁架隔件和SMPC縱梁的連接約束當作剛接處理，而實際節點采用螺栓緊固，未完全符合剛接的假設條件；②結構在裝配時由于外力干預導入了裝配應力，使得結構的自應力剛度矩陣發生變化，而該影響未在模型中考慮；③仿真未考慮材料的各向異性和非線性；④仿真未考慮激振中結構內部構件的相互碰撞導致的接觸非線性。

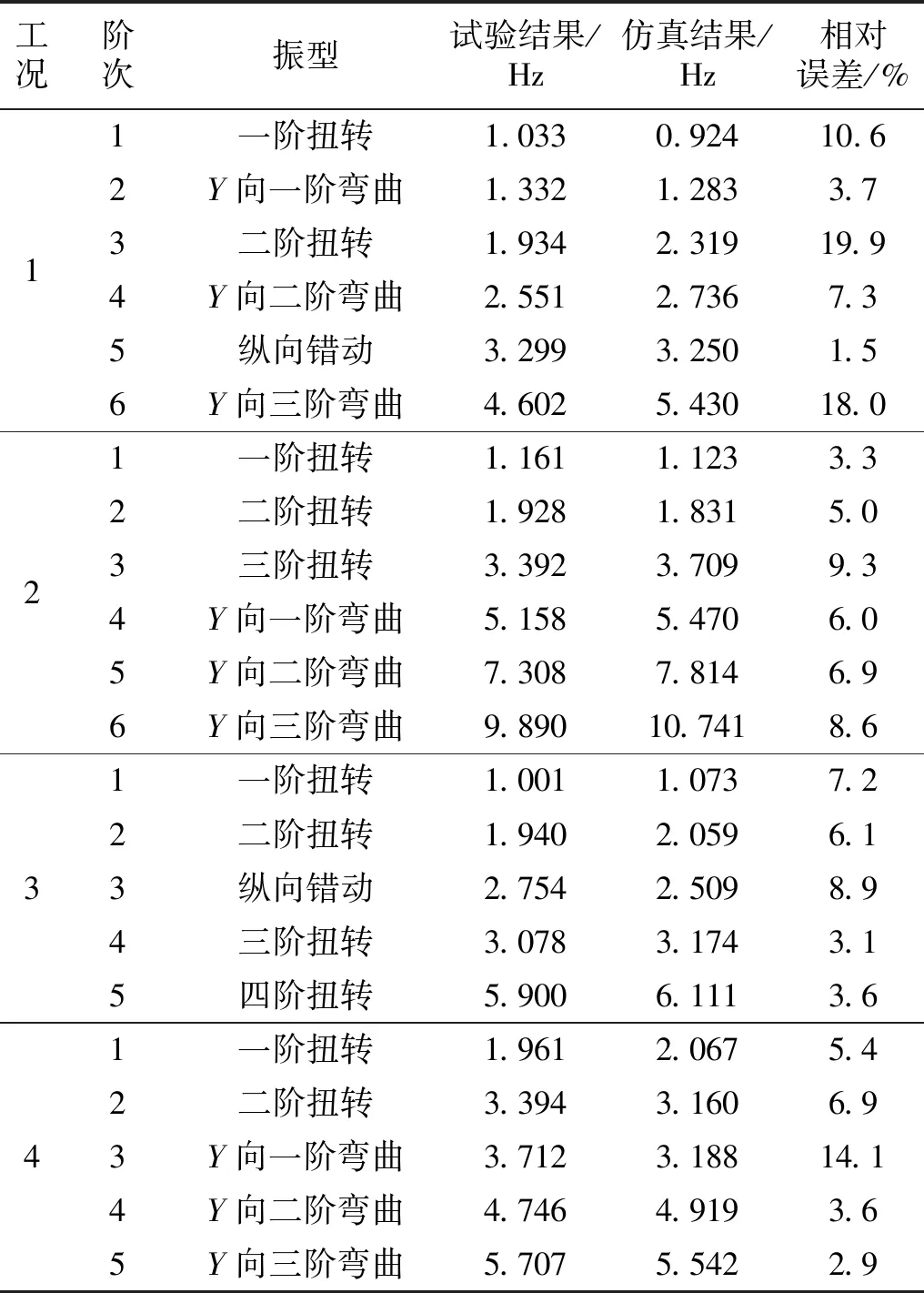
表3 模態分析結果與誤差Tab.3 Simulation results and errors of modal analysis

4 結 論

本文以重復折疊展開形狀記憶歷程后的五節SMPC可展桁架陣面天線為對象，首先通過動態法測得SMPC縱梁的彈性屬性，再對桁架天線進行了四種工況下的地面模態試驗和建模仿真分析，分析了結構的動力特性和影響規律，可以得到以下結論：

(1)各工況均首先出現扭轉模態振型，說明五節桁架結構扭轉剛度較彎曲剛度更低。

(2)通過設置加勁索施加預應力可提高桁架結構的整體剛度，也可提高結構沿縱向的抗剪能力。

(3)陣面板在施加預應力的工況下提供了扭轉剛度的貢獻。由于鉸鏈存在一定轉動自由度，陣面板對提高桁架結構的彎曲剛度無明顯貢獻。

(4)模態分析中考慮空氣阻力效應對陣面的影響，仿真結果與試驗結果吻合，各工況誤差在20%以內。