基于鎖相放大器的微擾型共面波導鐵磁共振測試參量研究

王 濤，郭牧晗，張 鵬，張瀚文，馮曉玉，王奕斐，范小龍

(蘭州大學 物理科學與技術學院，甘肅 蘭州 730000)

自旋電子學 (Spintronics)主要研究和調控電子的自旋屬性在其輸運過程中的行為. 目前，自旋電子學領域的研究重點之一是二維磁性材料的動力學性質，而鐵磁共振(Ferromagnetic resonance,FMR)測試是非常有效的測試方法[1]，其原理是：在微波磁場驅動下，磁矩繞著外加磁場方向做受迫振動(圓錐進動)，朗道-利夫希茲-吉爾伯特方程(Landau-Lifshitz-Gilbert equation，即LLG方程)可以很好地描述磁矩進動的軌跡，進而確定其磁性參量(例如：阻尼因子、垂直各向異性等效場等). 為了得到更多信息，往往需要在寬頻率范圍內進行FMR測量. 根據微波的傳播原理，FMR的測量可以分為封閉式(例如諧振腔)和開放式(例如共面波導)2種[2]. 諧振腔式封閉測試系統的測試精度很高，但是由于每個諧振腔的共振頻率是固定的1個或幾個值，若要實現寬頻帶的測量則需要在不同共振頻率的諧振腔中切換并且重新安裝樣品；而以共面波導為代表的開放式測試系統能夠在同一條件下進行連續測試，真正實現原位寬頻帶測試(頻率測試范圍與共面波導有關).

以矢量網絡分析儀(VNA)為核心的鐵磁共振(VNA-FMR)技術[3]是目前主流的寬帶調頻FMR測量技術之一，其已被證明是能有效表征超薄磁性薄膜和納米結構的技術靈敏. VNA-FMR技術的優點是將信號源和檢測器集成在1臺儀器中，并且在1次測量中同時提取每個端口的輸入和輸出信號，其缺點是需要仔細校準系統、設備成本高昂，且數據分析過程復雜. 另一種方法是將產生和檢測微波的組件分開，例如使用寬頻帶微波源產生微波，使用寬頻帶微波探測二極管進行檢測[4-5]. 研究表明：在測量導電鐵磁樣品時，可以將樣品直接用作探測器. 例如，各向異性磁電阻(AMR)導致的微波直流光電壓[6-7]以及自旋軌道矩[8]等效應使得可以對樣品進行鐵磁共振的電檢測(ED-FMR). 該方法設備成本較低且無需校準，使用納伏表即可測量電壓，且數據分析過程簡單. 然而ED-FMR要求對樣品進行圖形化以使測量電流穿過樣品，即樣品本身需要作為器件并入射頻傳輸線系統中. 通常將樣品切成條狀或刻蝕成Hallbar的形式，還需要引入額外的電極.由此可見，相對于VNA-FMR測試，ED-FMR測量方式極大降低了測試成本并簡化了分析步驟，但是提高了對樣品本身的要求. 結合以上2種方式各自的優點，2014年，E.Montoya提出了基于鎖相放大器的微擾鐵磁共振測試方法[3],也被稱為Phase-FMR[9]. 該方法既能在共面波導上直接測試磁性材料的鐵磁共振效應，又無需對樣品形狀進行處理，同時成本較低，數據分析過程簡單直接. 雖然該方法對實驗儀器、測試樣品的要求不高，但是在整個測試系統中可變參量較多，其中有很多設置能夠直接或間接影響測試結果的精度，如何正確對測試系統進行配置以得到真實的實驗結果是對實驗物理機制深入分析的前提.

整套測試系統可以分為2個相對獨立的部分：磁場控制系統和微波探測系統. 為了得到信噪比盡可能高的測試結果，探測部分以鎖相放大器為核心設備，鎖相放大技術是利用參考信號檢測和恢復微弱信號幅值和相位的精密測量技術，在近代物理研究中已普遍應用． 鎖相放大器能將微弱待測電信號從強烈的背景噪聲中提取、放大并進行測量，是微弱信號檢測與恢復的重要儀器，按電路特點分為數字和模擬2種類型，數字型鎖相放大器因具有優異且穩定的性能而被廣泛使用[10]． 由于鎖相放大器型號及相關參量較多，本文詳細分析了在基于數字型鎖相放大器(蘇黎世MFLI系列)的FMR測試系統中，各參量對測試結果的影響，總結和分析不同參量對測試結果的影響規律，給出了較理想的參量設置區間.

1 實驗原理與方法

1.1 寬頻帶微擾鐵磁共振的基本原理

寬頻帶微擾鐵磁共振的測試系統示意圖和實物圖如圖1所示. 在測試過程中，直流電磁鐵提供足夠大的外場(高于飽和場)使磁性樣品完全磁化，此時總磁矩方向沿外場方向. 在共面波導的輸入端通入射頻電流，經過共面波導產生與外磁場方向垂直的微波磁場，二極管功率計將共面波導輸出的微波信號轉換為電壓信號，該信號與微波功率成正相關. 由于磁矩繞外場方向進動(圖2)時吸收微波能量，因此通過檢測功率計輸出的連續電壓信號來反映磁矩的進動狀態. 當頻率達到磁矩的共振頻率時微波被強烈吸收，可以觀察到因電壓信號突然減小而表現出的吸收峰.

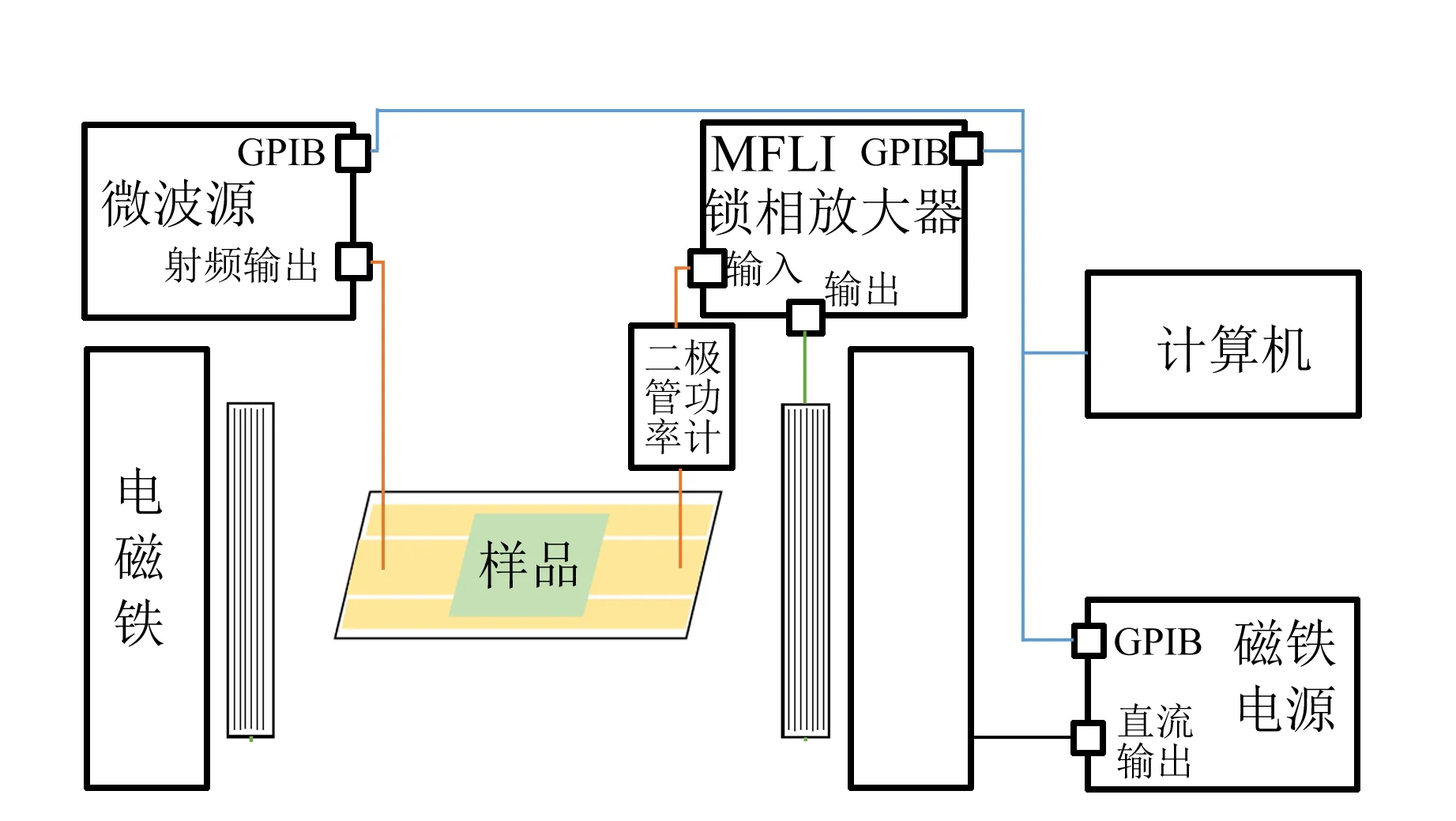
(a)Phase-FMR測試系統示意圖

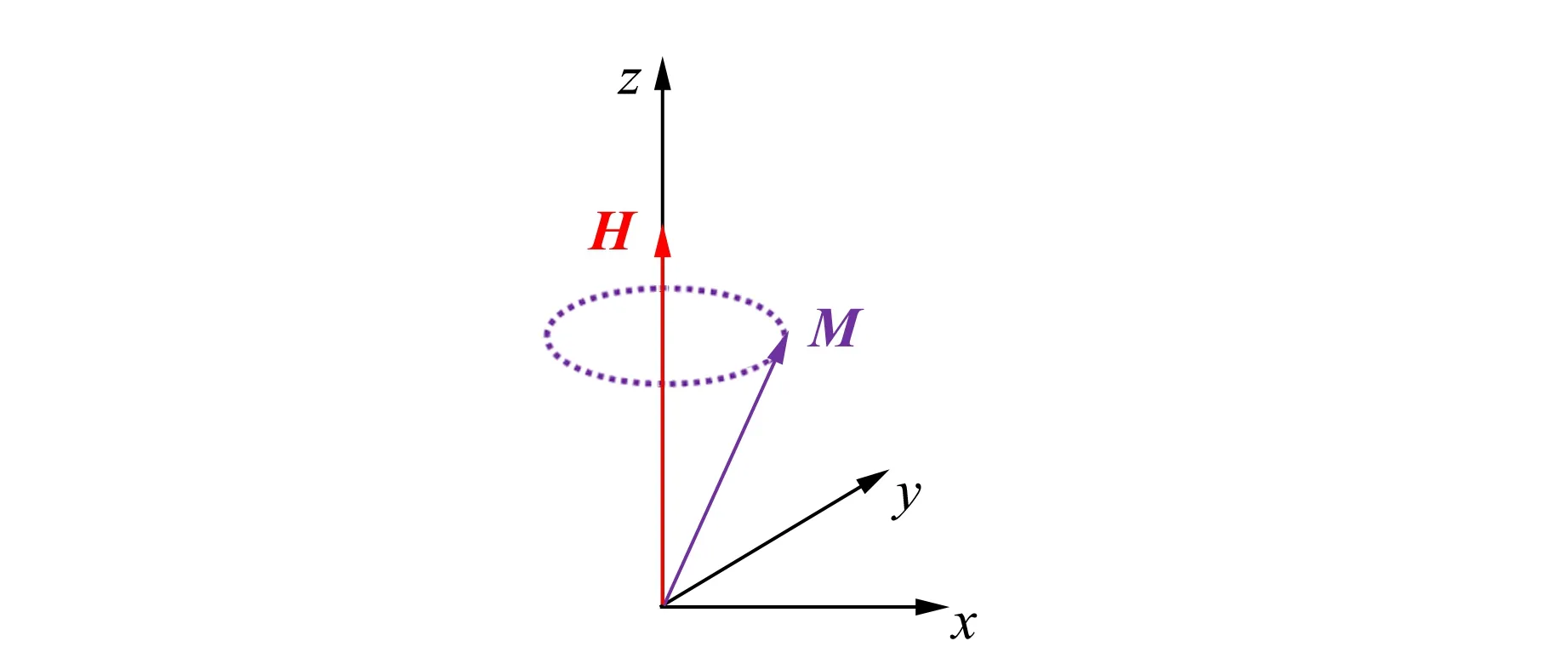
圖2 單疇顆粒中磁矩進動示意圖

微擾線圈的作用是在外磁場上疊加很小的交變磁場，由于鐵磁共振頻率與外磁場相關，因此功率計的輸出電壓也相應變成與微擾磁場同頻的交變信號(即微分信號)[11]，該交變信號由鎖相放大器接收并探測. 本系統所用鎖相放大器的輸出功率足以驅動微擾線圈，因此驅動微擾線圈的信號頻率由鎖相放大器決定，因而可以采用鎖相放大器的“自鎖模式”進行測試. 在“自鎖模式”下，鎖相放大器輸出的交變信號和處理輸入信號的解調器調用的是同1個振蕩器，從而在儀器內部實現閉環操作，也使設備外電路的接線更加簡單.

磁矩的動力學過程通常使用LLG方程描述，通過合理假設與數學處理，導出的磁化率虛部可以精確描述鐵磁共振曲線，通過分析共振場、線寬等參量的變化規律，可以得到材料的阻尼因子等性質. 相關公式討論[12]如下：

對于單疇顆粒，設外場H與總磁矩M在z方向做小角進動(Mz≈M)，如圖2所示，考慮微波磁場h以及受其影響導致的磁矩進動分量m，此時將

H≡(hx,hy,H+hz),M≡(mx,my,M+mz)

代入LLG方程

(1)

其中，γ為旋磁比，α為阻尼系數.可以將式(1)寫為分量形式：

(2)

可以得到發生鐵磁共振時的共振頻率ω、共振場Hr和線寬ΔH之間的關系為

γHr=ω,

(3)

(4)

張量磁化率[12]表示為

(5)

其中，χ和χa分別為磁化率的對角和非對角張量元，可以進一步寫為復數形式：

χ=χ′-iχ″,

(6)

χa=χa′-iχa″,

(7)

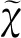
(8)

可見磁化率的虛部對應系統能量的損耗，在本實驗中這種損耗體現為二極管功率計輸出電壓隨外部條件改變(磁場或頻率)而出現的吸收峰.考慮到磁化率是張量，通過測量得到的鐵磁共振吸收曲線是磁化率張量元虛數部分的線性組合，可以表示為

(9)

其中，V為測量電壓，VD和VL分別為反洛倫茲線型和洛倫茲線型兩項的系數.

對于薄膜樣品，設外場H與總磁矩M方向如圖3所示，此時

圖3 二維薄膜樣品中磁矩進動示意圖

H≡(H+hx,hy,hz-mz),M≡(M+mx,my,mz)，

其中，-mz為退磁場，則分量形式為

(10)

令ωy=γH，ωz=γ(H+M)[13]，可以得到

(11)

當考慮二維薄膜的退磁場，此時線寬為

(12)

只有當H?M時，

(13)

同時鐵磁共振公式退化為式(9)，由于本設備使用微擾線圈對外磁場產生微擾，因此鎖相放大器實際測量電壓信號是式(9)的微分，即

(14)

1.2 鎖相放大器的基本原理

相敏檢波器(Phase sensitive detection, PSD)是鎖相放大器能夠在復雜背景噪聲中提取微弱信號的核心，經PSD處理的信號，還要通過低通濾波器，將其中的無用信號濾除，其結構圖如圖4(a)所示. 通常鎖相放大器的輸出參量有在直角坐標系下正交的X分量與Y分量，以及在極坐標系下的信號幅值R與相位角θ，各量之間的關系如圖4(b)所示.

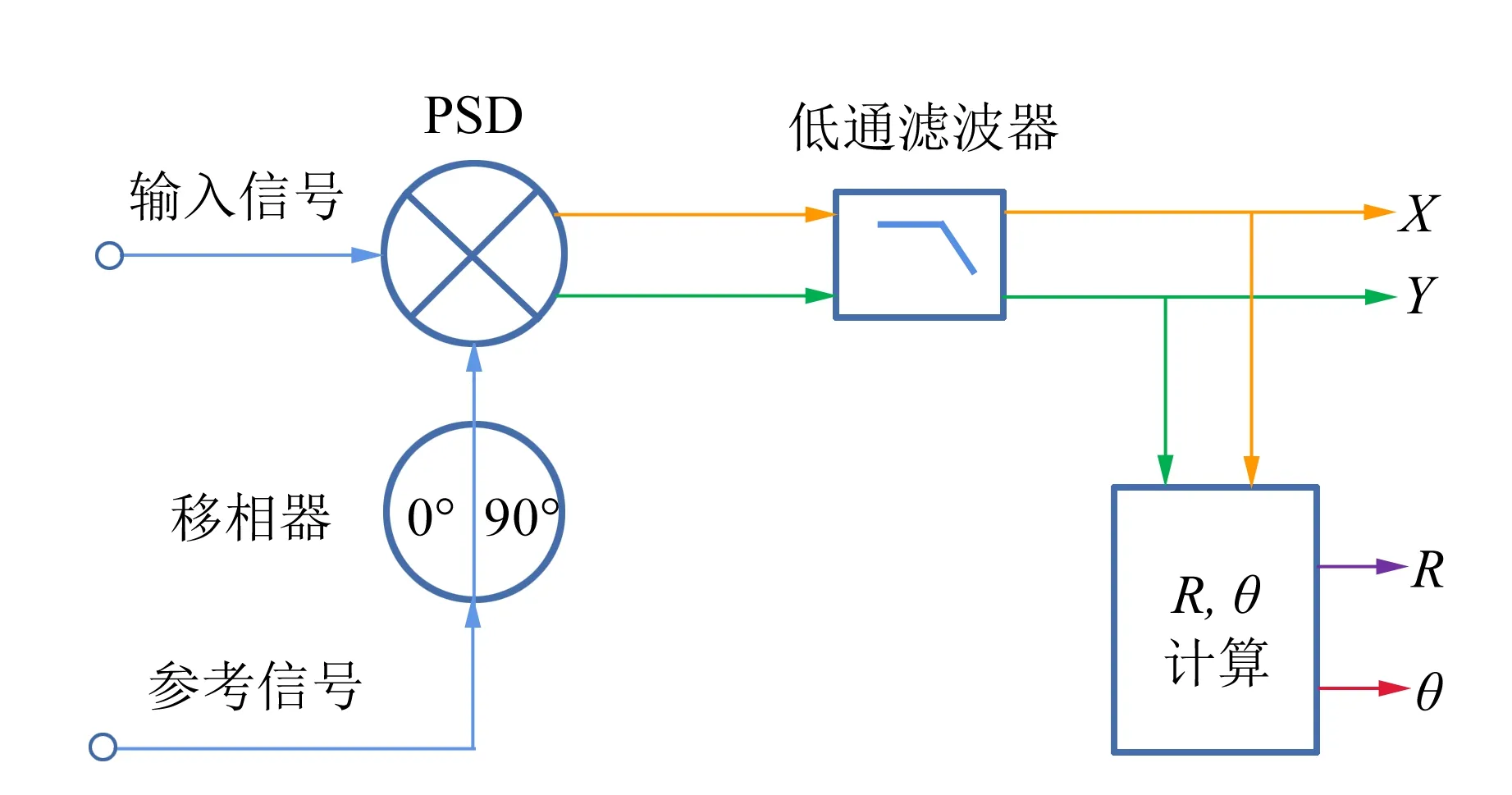
(a)MFLI鎖相放大技術器的結構框圖

為了簡化計算和幫助理解，采用簡單的數學形式進行討論：假設輸入信號Vin和參考信號Vr的數學形式分別為

Vin=Ainsin (ωint+φin),Vr=Arsin (ωrt+φr)，

其中，A，ω和φ分別為幅值、頻率和相位.經過PSD處理以后，得到信號為

cos [(ωin-ωr)+(φin-φr)]},

(15)

當二者頻率同為ω0時，即ωin=ωr=ω0,式(15)可寫為

cos (φin-φr)}.

(16)

即經過PSD處理后的信號變為直流信號和二倍頻信號的疊加. 低通濾波器的作用是將二倍頻信號以及與參考信號不同頻的信號(噪聲導致)濾掉，在參考信號幅值和相位已知的情況下，只需要探測直流信號的大小就可以得到輸入信號的幅值和相位.

2 影響鐵磁共振測試結果的參量分析

2.1 直流磁場的增加方式對測試結果的影響

在磁場相關的測量實驗中，電磁鐵的磁場電流增加有2種方式：掃場模式(SweepH)以及定點增加模式(SetH)，分別具有測量速度快與磁場精度高的優點. 在本實驗中，由于測量過程為微波功率的動態過程，因此磁場增加模式的影響不可忽略，此時測量的關鍵參量是磁場電流變化速率(Rate，RI). 為了論證前后的統一性，本文用磁場電流I的大小來表征磁場大小.

本實驗中所使用FeNi樣品通過磁控濺射的方式制備Fe20Ni80薄膜，其大小為5 mm×5 mm，厚度為7 nm. 為了使薄膜質量更好，在GaAs(100)基片上預先濺射了3 nm厚的Ta作為打底層；為了避免氧化，在FeNi樣品表面濺射了2 nm厚的Ta作為保護層. 如不特別說明，以下都在10 GHz，5 dBm的微波激勵下進行測試.

圖5中橫軸是磁鐵的勵磁電流，縱軸是鎖相放大器測量的Y通道電壓振幅，可見不同的磁場增加模式和變化速率對測試結果有顯著影響. 當采用掃場模式(在磁場緩慢增加過程中同時測量)時,隨著RI增加，鐵磁共振曲線的共振峰位置、線寬、線型、背景噪聲都會顯著變化，如圖5(a)所示. SetH下共振曲線的性質幾乎不受RI影響，如圖5(b)所示.

(a) Sweep H

利用式(14)對圖5(a)中的曲線進行擬合，結果如圖6(a)～(b)所示.Hr隨RI增加幾乎是線性的，ΔH與RI成平方關系. 當RI從0.01 A/s增加到0.15 A/s，Hr和ΔH的變化分別為38%和333%. 實驗中，當RI增加到0.20 A/s時，幾乎看不到共振峰的出現，故圖中并未展示. 定點增加模式下，當RI從0.01 A/s增加到0.20 A/s時，Hr和ΔH的變化率分別為3%和13%. 圖6(c)～(d)中陰影部分的數據點是RI從0.01 A/s增加到0.20 A/s之后，又減小到0.03 A/s和0.07 A/s的結果，此時測試結果與RI為0.20 A/s時幾乎一致. 考慮到電磁鐵磁芯的磁滯效應和微波導致的樣品溫度升高，3%和13%可以被認為是該系統在測試中的實驗誤差.

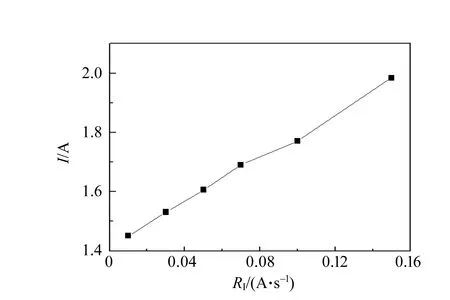
(a) Sweep H時Hr隨RI變化

在鐵磁共振測試時，磁場電流的增加應盡量采取SetH，同時應避免長時間測試，以及大微波功率導致的樣品溫度改變帶來的誤差. 從實驗結果可知：SweepH會對實驗結果帶來較大誤差. 結合背景信號，猜測這是磁場速度變化太快導致鎖相放大器時間常量不足的結果，因此在以下實驗中針對鎖相放大器的參量進行了探索.

2.2 鎖相放大器的參量對測試結果的影響

經過PSD處理的信號還要通過低通濾波器處理，將其中的高頻信號舍去，因此對于低通濾波器的選取將直接影響輸出信號. 低通濾波器的關鍵參量有2個：時間常量(Time constant，即τTC)和陡降(Roll-off, 即NRO)[10]. 前者主要作用是改變濾波器帶寬，從而實現對一定頻率范圍的信號進行測量，該參量也被稱為積分時間；后者是反映低通濾帶寬邊緣銳利程度的參量，值越大邊緣越陡峭，由于一般是由多階相同的RC電路串聯實現對陡降的調節，因此也被稱為滾降系數、濾波階數、分頻斜率、衰減斜率等.

2.2.1 鎖相放大器時間常量對測試結果的影響

為了驗證2.1的猜測，在不同τTC情況下進行測試，此時濾波階數為八階(48 dB/oct)，RI為0.03 A/s. 圖7(a)中，2種模式下由FMR曲線得到的Hr都隨τTC增加而增加. 在SweepH模式下，Hr的變化率達到26%；偏差較小的SetH模式下，Hr變化率也達到6%. 該結果顯示：為了得到準確的結果，τTC應盡量小. 在1%的誤差范圍內，認為在FMR測試中τTC設置為100 ms是合理的.圖7(b)中2種不同模式下的ΔH隨τTC增加成二次方關系，變化率分別為197%和27%. 此時τTC為100 ms，仍然是合理條件.

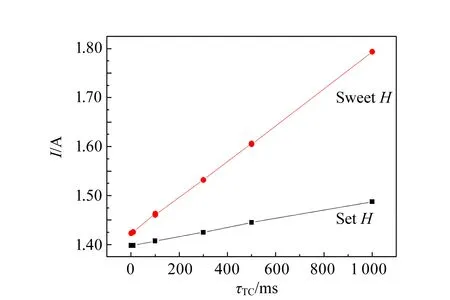
(a) τTC對Hr的影響

通過對比圖6(a)～(b)與圖7中Hr與ΔH在不同條件下的變化規律，不難發現:在SweetH中帶來誤差的關鍵是信號采集速率，即RI與τTC的匹配. 當RI過大，鎖相放大器沒有足夠的時間進行信號處理，此時會導致誤差增加，而且此誤差的增加與失配程度線性相關；而τTC過大，鎖相放大器在信號處理的過程中又測量到另1個狀態的數據(SweepH模式)，因此誤差也會線性增大. ΔH是共振峰的半高全寬[式(12)]，是對FMR曲線的整體分析，測量誤差也因此不斷積累，最終ΔH的誤差與失配程度呈二次方關系. SetH的結果表明：當盡量滿足信號采集速率匹配時，τTC過大仍然會導致誤差的不斷增大，猜測這是由于實際的微分信號在非共振情況下并不嚴格為0導致的信號積累.

2.2.2 鎖相放大器濾波階數對測試結果的影響

由2.2.1的結果可知，在其他條件固定的情況下，τTC越小，Hr與ΔH結果越精確，因此在SetH條件下(τTC為1 ms時，RI為0.03 A/s)，改變濾波階數進行測試. MFLI鎖相放大器的NRO共有八階，分別是一階(6 dB/oct)、二階(12 dB/oct)、三階(18 dB/oct)、四階(24 dB/oct)、五階(30dB/oct)、六階(36 dB/oct)、七階(42 dB/oct)和八階(48 dB/oct). 圖8 (a)為不同濾波階數下的測試結果. 可以看出：NRO并不影響測試曲線的峰型和位置，但是過小的NRO會導致測量噪聲增大. 提取圖8(a)中虛線范圍內曲線背景信號進行處理，即在磁場電流為1.8～2.4 A范圍內背景信號的平均值和標準差如圖8 (b)～(c)所示，NRO在二階以上的噪聲已經趨于穩定. 從圖8(d)可以看出：在二階以上時，信噪比均超過36 dB. 需要注意的是，由于很多材料的共振峰會出現多峰耦合和多個強度不同的峰等情況，因此，NRO也不宜過大，如果過于追求曲線的光滑，可能會導致較弱的信號未能被檢測到. 因此實際實驗過程中，應考慮待測樣品的性質，從而調整到合適的參量.

(a) 鐵磁共振曲線

2.2.3 鎖相放大器不同參量輸出的測試結果

雖然鎖相放大器在不同坐標系下的輸出信號(X，Y)和(R，θ)是等價的，但是在FMR測試中通常選用直角坐標系下X或者Y信號進行數據擬合，原因是：

1)X與Y信號分別對應輸入信號與參考信號同相和正交的2個分量，同時包含輸入信號的大小(R)和方向(θ)信息. 由于本實驗需要通過式(14)得到FMR的Hr和ΔH，對X[圖9(a)]和Y[圖9(b)]通道曲線的擬合會得出同樣的結果，區別是系數VD與VL不同.

2)R與θ(極坐標系下)各自包含FMR部分信息，處理起來相對復雜：R信號[圖9(c)]的FMR曲線理論上也可以利用式(14)進行擬合，但是根據其定義[圖4(b)]，R信號的值永遠大于等于0，在某些情況下(例如X與Y通道的信號都經過1次變號),R信號的數值由于無法描述方向從而導致曲線變形，此時需要結合θ信號[圖9(d)]將其還原為X或者Y信號再進行處理.單獨處理θ信號也存在類似的問題.故實驗上多選用X與Y通道信噪比較高的曲線進行分析.

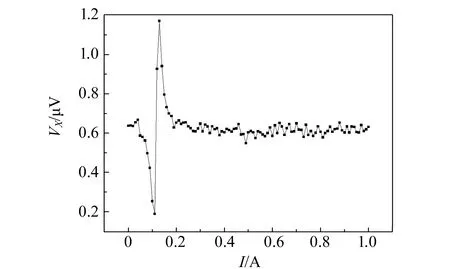
(a)X信號

2.3 微擾磁場變化對測試結果的影響

微擾部分也是影響測試結果準確性的因素. 采用讓鎖相放大器本身輸出的交流電壓信號驅動微擾線圈的方法，通過鎖相放大器的自鎖功能采集得到功率探測器輸出的信號中與該交流信號同頻的部分. 因此，鎖相放大器輸出的交流電壓信號的幅值與頻率決定了對樣品鐵磁共振信號的微擾程度，以下是不同微擾條件下對YMn6Sn6樣品的測試結果.

2.3.1 微擾磁場振幅的影響

在微波頻率為4 GHz，微擾頻率為133 Hz條件下，改變微擾電壓VP，測試結果如圖10所示. 由圖10(a)可見(顏色代表不同電壓大小)，當VP>1 V時，出現明顯的共振信號；當VP>2 V時，曲線信噪比較高. 將不同VP下的FMR曲線由式(14)進行擬合，得到結果如圖10(b)～(d)所示,VL與VD隨VP的增加而單調增長，導致FMR曲線的總信號幅度增加.

Hr和ΔH對于VP的響應表現為分段曲線,如圖10(c)～(d)所示：在0～2 V時，Hr和ΔH基本不變；當VP>2 V時，Hr和ΔH隨VP的增加呈線性增長(圖中紅色虛線部分所示). 原因是當微擾線圈的激勵電壓過大(超過2 V)時，產生的微擾磁場對直流磁場產生補償，導致達到共振條件需要更大的直流磁場. 圖10(c)顯示隨VP的增加，Hr的偏差小于1%，可見微擾磁場對Hr的影響可以忽略. ΔH是對整體FMR曲線性質的分析，因此其誤差比Hr大. 在相同情況下，隨VP的增加，ΔH偏差達到30%[圖10(d)]. 因此，在本系統中比較理想的情況是VP取值為1～2 V，VP過小則信號微弱導致誤差較大，VP過大則導致微擾磁場對直流磁場產生影響，引入新的誤差.

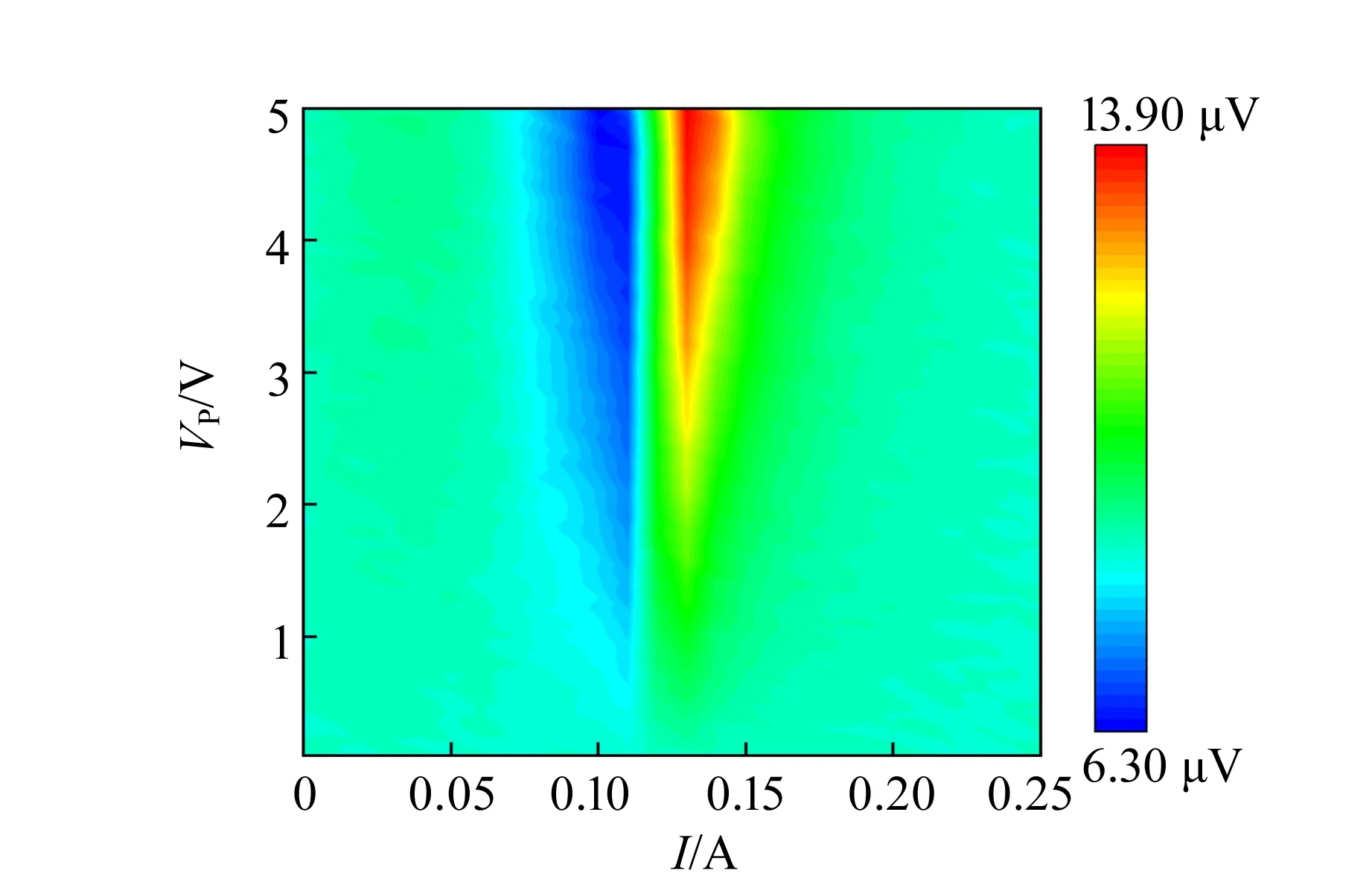
(a)不同VP下X信號的FMR強度圖

2.3.2 微擾磁場頻率的影響

只改變微擾頻率fP，結果如圖11所示. 由圖11(a)可見(顏色代表不同電壓大小)，在fP極低條件下(例如33 Hz)就可以得到明顯的共振曲線. 為了觀察fP對FMR曲線的影響，將不同fP下的FMR曲線通過式(14)進行擬合，結果如圖11(b)～(d)所示. 隨著fP增加，VL與VD逐漸減小，這是因為頻率提升導致微擾線圈的阻抗增加，實際產生的磁場反而有所減小. 圖11(c)～(d)中Hr和ΔH隨fP的增加而略微減小(減小幅度分別為2.3%和6.1%)，也證明了該過程. 值得一提的是，在圖11 (c)中33～200 Hz范圍內Hr迅速減小(1.6%)，而此時ΔH基本保持不變[圖11(d)]，且整體振幅[圖11(b)]保持在較高量級. 因此，微擾信號的振幅設置范圍為1～2 V，頻率范圍為33～200 Hz.

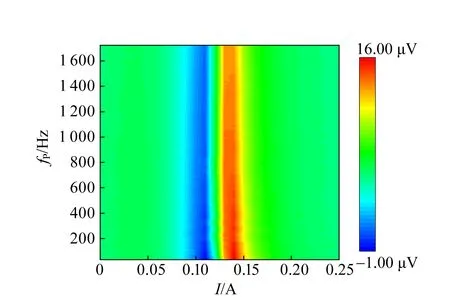
(a)不同fP下X信號的鐵磁共振圖

3 結束語

本文設計并實現了基于鎖相放大器的微擾型共面波導鐵磁共振系統，該系統可以在室溫下對磁性樣品實現原位、無損的鐵磁共振測試，并且無需對樣品進行微納加工等復雜操作. 通過理論推導，得出該系統鐵磁共振信號的擬合公式，并以此為基礎，結合參量下的實驗結果，得到了最優參量區間.由于該系統具有易搭建、成本低的特點，可以對高校近代物理實驗中FMR內容進行補充或者替代. 本實驗不僅可以幫助學生學習和掌握鐵磁共振原理，還可以幫助學生掌握鎖相放大器的相關理論與技術. 通過實驗探究磁場增加模式、時間常量、陡降等對測試結果的影響，還可以使學生熟悉并掌握實驗中優化測量參量的方法．