浮沉子實驗中不可逆現象的研究

孫金晶，王鑒純，王春梅，張 杰，夏成杰

(華東師范大學 物理與電子科學學院，上海 200241)

浮沉子是由法國科學家笛卡爾(1596—1650)創造的實驗裝置，作為趣味物理實驗，常出現在科普演示與科學課外小組活動中，其實驗材料易得，實驗現象豐富，可以激發學生的學習興趣. 2021年，第12屆中國大學生物理學術競賽(CUPT)題目6就與浮沉子直接相關，試題為:簡單的浮沉子(例如部分裝有水的倒置試管)被放置在裝有水的長直管中,增加管中壓強會使浮沉子下沉. 當浮沉子到達一定深度，即使改變管內壓強至初始值，它都無法返回表面. 研究這一現象，以及相關參量如何影響該現象.

浮沉子體系看似簡單，但實際涉及的物理機制較為復雜. 對于這一系統，不可逆現象是關鍵. 已經有文獻給出其運動的基本理論[1-2]以及發生不可逆現象的臨界條件[3]，但是對于理論模型中的簡化近似缺乏清晰的解釋，也未能通過精確可控的實驗加以驗證. 為驗證基礎的理論模型和修正后的理論模型是否適用，結合浮沉子的特點，需要精確、可控的實驗裝置進行實驗. 本文從浮沉子的制作、氣壓控制、圖像處理等方面深入考慮，設計了有效且精確度高的裝置及實驗方法，從浮沉子運動和是否可逆等角度開展實驗研究，所得實驗結果與理論一致. 在對浮沉子問題的分析和解決過程中，既有理論分析的深化和完善，又有實驗設計的修改和補充，還能綜合運用Matlab等軟件進行數值模擬、圖像追蹤處理，學生自主開展文獻查閱和學習. 該過程對培養學生解決物理問題的能力具有重要作用，浮沉子適合作為本科生的初級科研訓練，并融入大學物理實驗課程[4].

1 實驗原理

1.1 理論模型的構建

對浮沉子進行模型構建，實驗參量及定義如圖1所示.在此體系中，將浮沉子定義為倒置的試管及其內含的氣柱，并且將二者作為整體進行受力分析.當管內壓強p增大時，通過靜水壓強傳遞，浮沉子內部氣體壓強增大，體積減小，所受浮力減小.當壓強p持續增大，浮沉子所受浮力減小直至小于重力與表面張力之和，浮沉子開始下沉.

(a)裝水長管及其內部的試管

1.2 浮沉子中氣柱狀態分析及受力分析

實際實驗中，浮沉子內氣柱壓強為

pgas=p0+ρlgh+pd,

(1)

其中，pd為由流體運動而產生的壓強.利用Comsol軟件進行數值模擬，發現當浮沉子的運動速度在符合實際實驗的±0.3 m/s范圍內且加速度小于0.1 m/s2的情況下，運動流體產生的壓力僅為重力的3%，可以將其忽略. 此外，分別使用理想氣體狀態方程的等溫和絕熱過程以及范德瓦爾斯方程，計算當氣柱體積變化0.5 cm3時的體積-壓強變化曲線(圖2)，發現在實驗條件下，由不同的狀態方程和熱力學過程計算出的壓強-體積關系的區別不大.

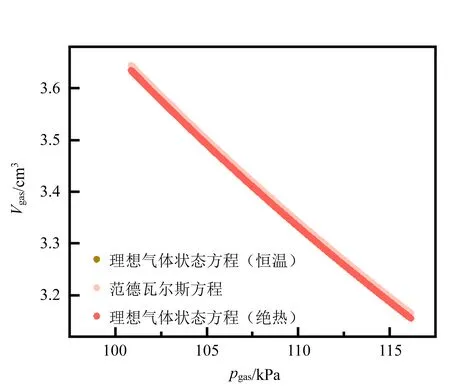
圖2 數值計算浮沉子氣柱體積隨壓強變化

因此，浮沉子內氣柱在浮沉子運動的全過程中可近似看作發生等溫變化的理想氣體，由理想氣體狀態方程得到：

p0V0=pgasVgas=(p+ρlgh)lgasSt,

(2)

從而解得氣柱長度為

(3)

分類討論完全浸沒與未完全浸沒的情況下，計算得到浮沉子所受浮力為

Fb(x)=ρlgV排=

(4)

需要指出，在這里采用了靜態液體中的浮力表達式，嚴格來說，它與在流體中運動的物體所受浮力存在區別.在下文計算浮沉子的運動過程中，將運動流體對物體額外的作用力以唯象的形式加入.通過將理論計算結果與實驗數據對比，該近似非常合理.

在上述近似下，浮力是深度的函數，所以引入浮力與重力之和的等效勢能[3]：

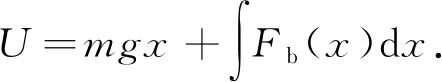
(5)

將不同管內壓強下，浮沉子所受到的重力、浮力以及等效勢能隨其位置x的函數關系繪制如圖3所示，其中各參量取值均符合實驗實際情況.

圖3展示了管內壓強增加時浮沉子的運動全過程：壓強增大，勢能曲線中的極小值點在某臨界壓強下(1.08p0)消失，此時浮沉子開始下沉.此過程中勢能曲線極小值點消失的過程也是較為常見的物理現象——折疊突變現象(Fold catastrophe)[3,5].當管內壓強恢復初始的標準大氣壓時，勢能曲線出現極大值(即勢壘).若此時下沉的浮沉子已越過勢壘或者其動能可使之越過勢壘，則將繼續下沉；反之將上浮.浮沉子在勢壘位置所對應的深度的浮力滿足

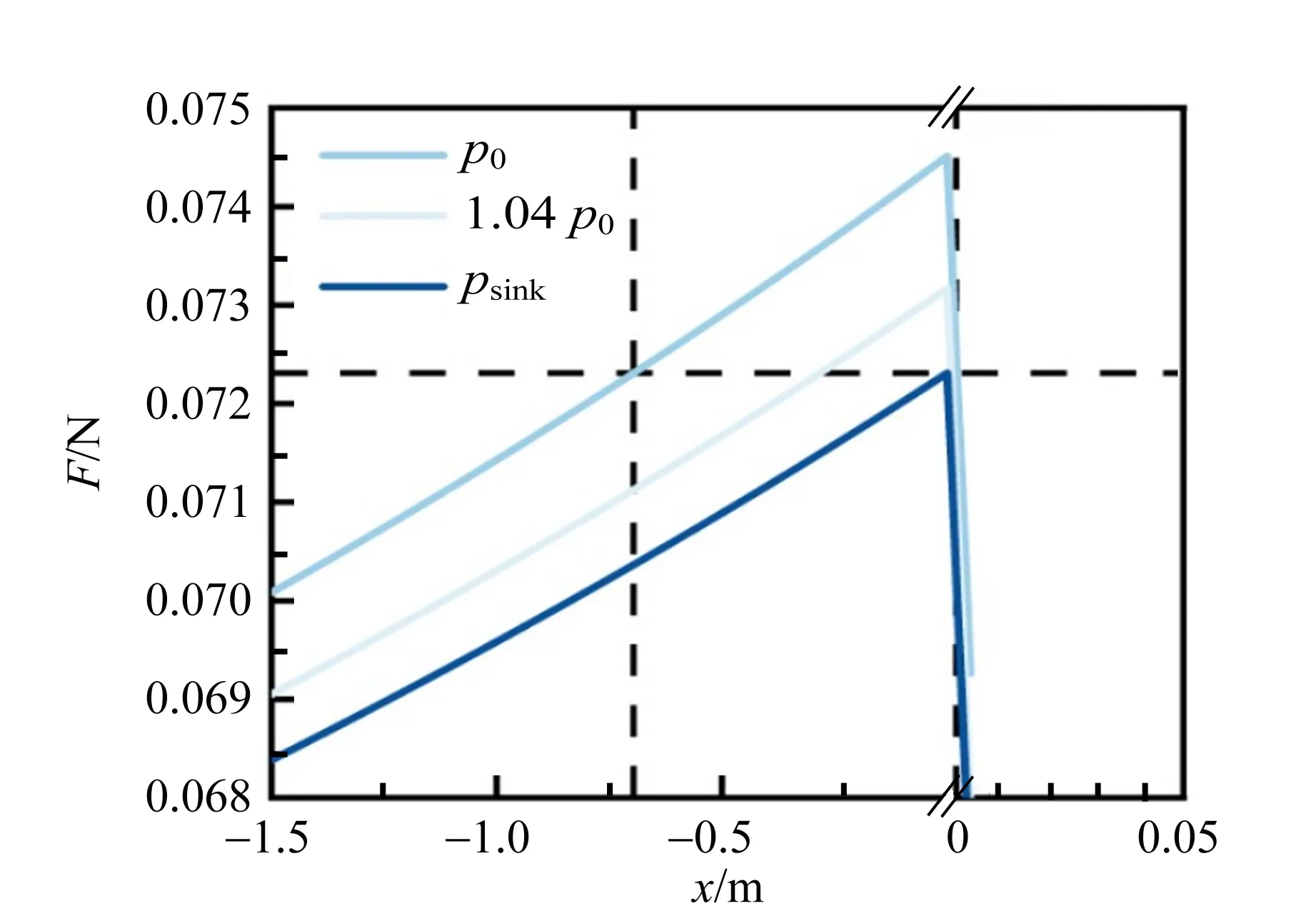
(a)重力與浮力

Fb=mg,

(6)

將此深度定義為臨界深度.聯立式(4)和(6),解得臨界深度為

(7)

1.3 浮沉子的動力學分析

結合牛頓第二定律，浮沉子的動力學方程可以表述為

(8)

其中，fl表示運動的浮沉子所受到的流體阻力.雖然其嚴格的表達形式需要用復雜的流體力學計算，但是對比實驗、理論和模擬計算均表明，使用斯托克斯經驗公式計算當前體系中的流體阻力，能夠較好地解釋實驗現象.除此之外，浮沉子在水面附近運動時還會受到表面張力作用，其具體大小不易測量[6-7]，但是結合實驗數據進行計算，發現表面張力比重力、浮力等主要作用力小2個數量級，因此可以被忽略.代入浮沉子和氣壓的相關參量，數值求解式(8)，得到不同加壓持續時間下，浮沉子的x-t和v-t圖像(圖4)，其中x=0表示浮沉子的初始深度.

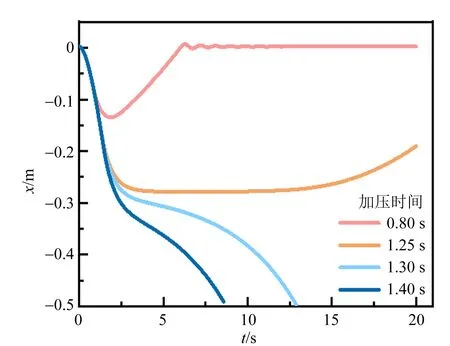
(a)x-t關系

從數值計算結果中可以看出，如果浮沉子在水下運動速度為0的深度小于臨界深度，則最終會上浮，如圖4中加壓0.80 s和1.25 s情況；若大于臨界深度，則最終沉底，對應于圖4中加壓1.30 s和1.40 s的情況. 并且可以看出，在最終上浮或下沉的臨界情況附近，浮沉子的運動對加壓過程的持續時間非常敏感：1.25 s和1.30 s的加壓持續時間只改變了0.05 s，浮沉子只在臨界深度附近停留了幾秒，便表現出截然不同的后續運動情況. 這也反映了在圖3勢能曲線中，臨界深度對應于非穩定平衡點的事實.

上述理論分析表明：由于實驗環境中的各種擾動、實驗儀器響應時間以及實驗人員的反應時間限制，原則上不可能控制浮沉子恰好靜止于不穩定平衡點，即無法通過調整參量而將浮沉子正好控制在臨界深度附近并加以測量. 因此，必須通過不斷改變參量，使浮沉子盡量接近臨界深度的夾逼方法來測定臨界深度.

2 實驗裝置及方法

2.1 實驗裝置

實驗裝置如圖5所示. 使用鋁型材搭建支架，用來固定亞克力長管并保證其豎直，上方的鋁型材可壓實橡膠塞以保證裝置氣密性良好. 橡膠塞連接2根玻璃導管，一根通過橡皮管與注射器相連，并采用可控參量的注射泵推動注射器以精確控制長管內的壓強，可設定每次實驗的注入速度和注入量，減小人為操作的誤差；另一根玻璃導管通過橡皮管連接數顯壓差計，實時獲取管內氣壓和大氣壓的差值，并用電腦記錄，從而獲取實驗過程中管內氣壓隨時間的變化圖像. 實驗中使用的浮沉子是采用3D打印制作的平底試管，其幾何形狀的參量可以精確到0.1 mm；為了便于對浮沉子進行圖像追蹤與處理，在試管壁上做了黑色標記.

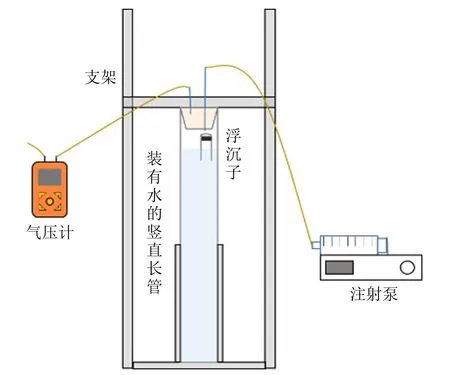
圖5 實驗裝置示意圖

2.2 圖像處理

為獲取浮沉子的位置數據，利用Matlab軟件編寫了圖像處理程序. 在Matlab中導入視頻并打開其中1幀圖像，對視頻圖像進行二值化處理，得到浮沉子的黑色標記區域的二值圖像，如圖6所示，進而獲取二值標定區域的最高位置坐標，結合圖像像素大小與實際大小的定標數據，可換算得到浮沉子的位置.

圖6 圖像二值化處理示意圖

為避免相機畸變引入定標誤差，實驗選取Nikon D810單反相機配置標準鏡頭，實驗裝置距離相機3 m，并且將圖像呈現在相機畫面的中間部分，裝水長管橫向視角小于1.5°，可以忽略橫向畸變. 將裝水長管的橫向直徑作為定標尺寸，利用像素換算獲得圖像中物體的測量長度. 長管的實際高度為1.500 m，經像素定標得到測量高度為(1.496±0.008) m，在誤差允許范圍內，可認為相機畸變對實驗測量幾乎無影響.

2.3 浮沉子運動全過程的探究

由3D打印制作不同參量的浮沉子樣品，并精確測量其實際大小. 用注射器向浮沉子內注入一定體積的水，放入裝有水的長直管中. 初始管內空氣與外部連通，為1個大氣壓，隨后固定橡膠塞及上方鋁型材，以保持管內氣體密閉. 啟動壓差計，開啟相機，啟動注射泵. 加壓一定時間后，浮沉子開始持續下沉，暫停注射泵以保持管內壓強恒定. 當浮沉子運動到一定深度，快速斷開連接注射器的橡皮管，使長管內迅速恢復初始的標準大氣壓，浮沉子上浮或者繼續下沉. 持續拍攝直至浮沉子運動結束. 最后，利用圖像處理程序提取視頻數據，得到浮沉子運動全過程的深度-時間圖像.

2.4 臨界深度的測量

由于浮沉子的臨界深度為不穩定平衡點，原則上不可能使浮沉子長時間停留在臨界深度所對應的位置，因此無法直接測量臨界深度. 依據1.3探討的情況，臨界深度是決定浮沉子最終上浮或者下沉的直觀物理量：最終上浮的浮沉子勢必無法達到并且跨越臨界深度，而最終沉底的浮沉子則勢必跨越臨界深度. 所以，對同一初始條件的浮沉子多次改變加壓持續時間，得到多條上浮、下沉的深度-時間圖像，通過不斷夾逼的方式得到臨界深度的范圍，即浮沉子最終上浮的最深處和下沉的最淺位置的范圍. 每組參量進行10次重復實驗，實驗測得的臨界深度標準差為±5 cm. 該方法符合物理過程，是較為理想的臨界深度測量方法.

3 實驗結果及分析

實驗所用浮沉子參量如表1所示.

表1 實驗所用浮沉子參量

3.1 阻力系數的獲得

利用Comsol軟件，采用圓柱形氣柱在液體中的受力模型(圖7)，代入實際測量的實驗參量，數值模擬得到斯托克斯公式的相關阻力系數為0.092.

圖7 Comsol模型計算阻力系數

3.2 加壓持續時間對浮沉子運動的影響

通過改變停止加壓到恢復初始氣壓的間隔時間來改變加壓持續時間，得到不同加壓持續時間下浮沉子的運動過程. 實驗結果如圖8所示，在恢復壓強后浮沉子運動情況與理論對照非常一致，同時，相同條件的實驗現象可重復性較高，均符合臨界深度判定，且理論臨界深度與實驗夾逼范圍一致. 本實驗的合理性得到驗證，實驗與理論結果較為吻合.

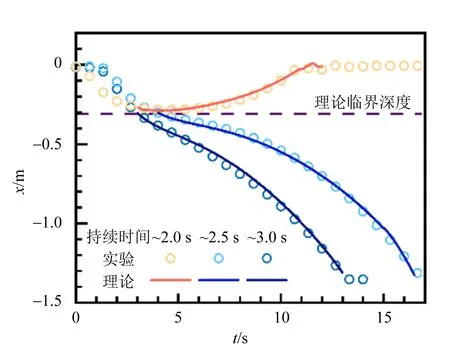
圖8 浮沉子不同運動的實驗與理論對比

3.3 各參量對臨界深度的影響

基于上述裝置和實驗處理系統，本實驗還探究了初始氣柱長度、浮沉子長度和浮沉子內截面積等參量對浮沉子臨界深度的影響，如圖9～12所示. 由1.2可知，臨界深度滿足式(7)，臨界深度隨各參量改變的實驗結論如下：浮沉子初始氣柱長度越大，臨界深度越深，二者基本呈線性關系；實驗范圍內，浮沉子長度越小，臨界深度越深；實驗范圍內，浮沉子截面積越大，臨界深度越深.

圖9 初始氣柱長度對臨界深度的影響 (浮沉子1)

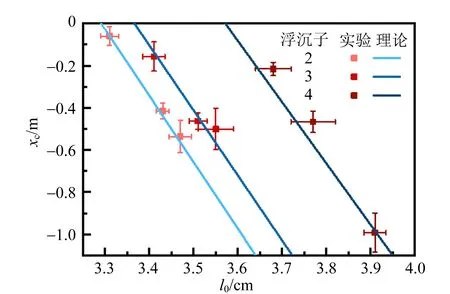
圖10 浮沉子長度對臨界深度的影響

圖11 浮沉子截面積對臨界深度的影響

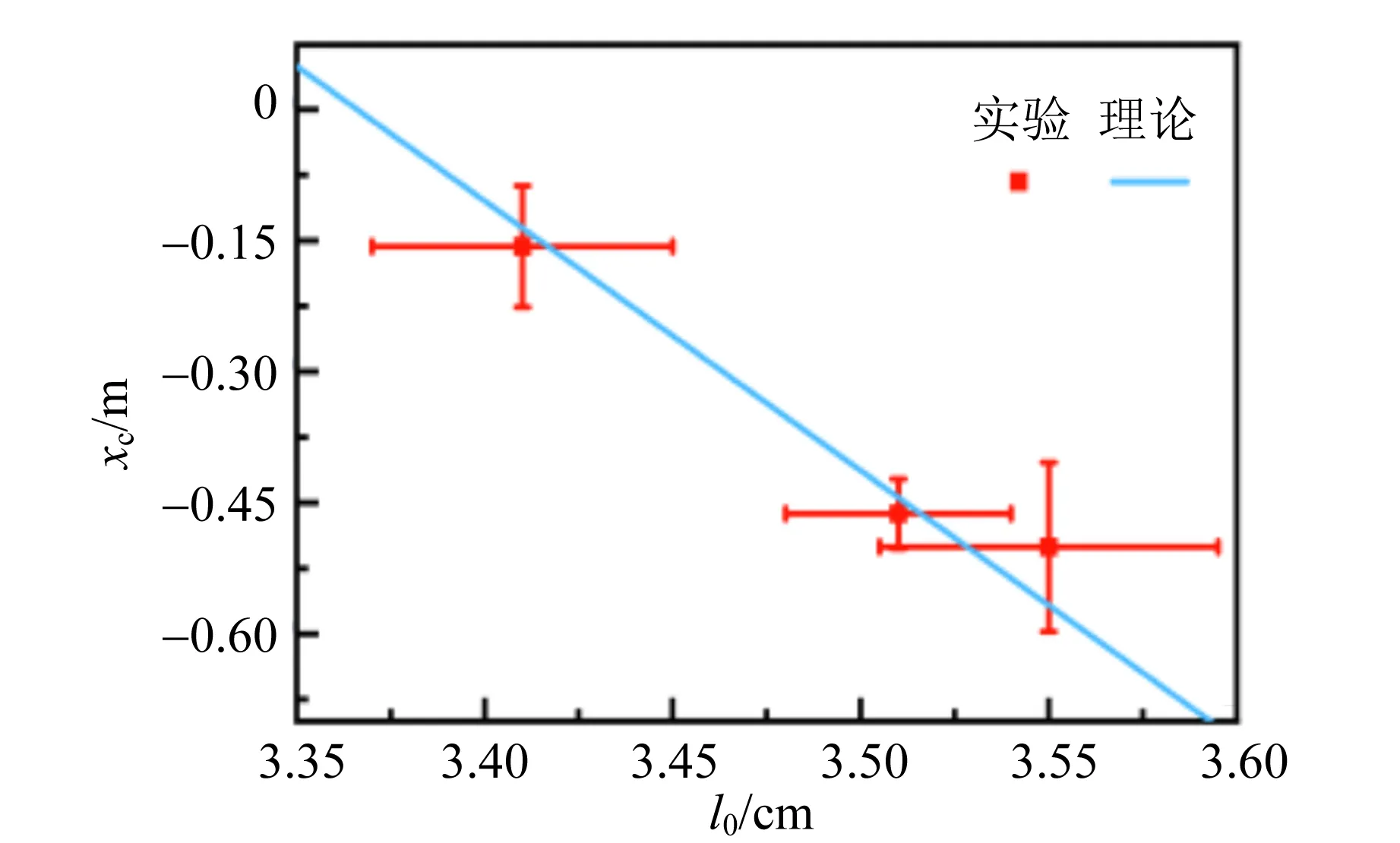
(a)浮沉子5

初始氣柱長度誤差棒(橫向)主要表征對氣柱長度進行追蹤帶來的誤差，即由于測量氣柱長度所占用的像素點數量較小，且液體邊界較為模糊，因此引入誤差棒表示測量精度；臨界深度誤差棒(縱向)用以體現夾逼法確認臨界深度時產生的誤差，其上下界代表夾逼的范圍以及長度測量的誤差. 在誤差允許的范圍內，實驗結果與理論符合.

4 結束語

本文設計了參量可控的裝置以及配套的實驗方法和圖像數據處理方法，并研究了浮沉子的運動過程，利用夾逼的方法獲得了浮沉子不可逆現象的臨界深度，且研究了影響臨界深度的多個參量，驗證了基礎的理論模型和修正后的理論模型的適用性. 該實驗操作簡單，理論思路清晰，可以作為大學物理實驗的拓展內容，培養學生分析、研究與解決問題的能力，實驗操作能力，資源獲取、整合以及綜合運用的能力.