基于多指標(biāo)優(yōu)化TQWT和TEO的軸承聲發(fā)射故障診斷

陳俊潼，周鳳星，嚴(yán)保康，汪峰

(武漢科技大學(xué)信息科學(xué)與工程學(xué)院，湖北武漢 430081)

0 前言

滾動軸承是被廣泛應(yīng)用在旋轉(zhuǎn)機械中的支承元件，其性能和工作狀態(tài)對機械設(shè)備的正常運轉(zhuǎn)至關(guān)重要[1]。因此針對滾動軸承故障診斷，尤其是早期故障診斷的研究具有重大現(xiàn)實意義。

聲發(fā)射(Acoustic Emission，AE)信號檢測技術(shù)是一種新型無損檢測技術(shù)，具有響應(yīng)頻帶寬、靈敏度高的特點，可以有效提取早期微弱故障信號。但是實際采集的軸承聲發(fā)射信號帶有大量噪聲和調(diào)制成分，有必要對其進行處理，提高信噪比并解調(diào)，以便提取故障特征信息。

對軸承故障聲發(fā)射信號這種非平穩(wěn)信號，小波變換降噪是一種有效的方法。孫守保等[2]通過AR模型和最小熵解卷積(Minimum Entropy Deconvolution,MED)濾波結(jié)合復(fù)Morlet小波變換成功提取了聲發(fā)射信號的雙沖擊特征。張瑞等人[3]使用經(jīng)驗小波變換(Empirical Wavelet Transform，EWT)構(gòu)建小波濾波器組，實現(xiàn)對聲發(fā)射信號的消噪和特征提取。徐嗣嘉等[4]將小波包能量譜與共振解調(diào)法結(jié)合，通過分析子頻帶能量提取了聲發(fā)射信號特征。以上研究證明了小波變換在軸承故障聲發(fā)射信號處理的有效性。但是經(jīng)典小波變換對信號的分解效果依賴于小波基的選取，如果小波基與故障特征不匹配會導(dǎo)致故障特征成分的損失，并在子頻帶中引入無關(guān)噪聲。可調(diào)Q因子小波變換(TunableQfactor Wave-let Transform,TQWT)是在小波變換基礎(chǔ)上改良的時頻分析方法，相比于經(jīng)典小波變換，TQWT可對品質(zhì)因子Q、冗余度r、分解層數(shù)J三個參數(shù)進行調(diào)節(jié)，實現(xiàn)小波基與待提取故障特征的最佳匹配，從成分復(fù)雜的信號中提取出微弱的故障特征分量。目前TQWT方法主要應(yīng)用在振動信號上，關(guān)于聲發(fā)射信號TQWT研究還很少。孔運等人[5]設(shè)計自適應(yīng)TQWT濾波器算法，結(jié)合沖擊特征指標(biāo)實現(xiàn)了信號降噪和特征提取。余發(fā)軍和周鳳星[6]依據(jù)譜峭度指標(biāo)用TQWT對信號進行分解，有效提取了早期故障沖擊成分。張龍等人[7]利用最小熵解卷積突出信號沖擊特征，再用TQWT對其進行分解重構(gòu)，得到軸承故障特征信號。

Teager能量算子能夠跟蹤信號的瞬時能量，并對信號解調(diào)，與Hilbert解調(diào)法相比，能量算子解調(diào)法能抑制端點效應(yīng)，近年來越來越多的研究者將其運用在軸承故障診斷中。楊斌等人[8]將自相關(guān)變換與能量算子解調(diào)法結(jié)合，提取出故障特征。郭璐等人[9]通過快速傅里葉變換得到Teager能量譜圖，輸入卷積神經(jīng)網(wǎng)絡(luò)，得到故障診斷模型。

基于以上分析，本文作者提出一種多指標(biāo)優(yōu)化TQWT與Teager能量算子相結(jié)合的故障診斷方法，通過改進的TQWT方法對原始聲發(fā)射信號進行自適應(yīng)分解和頻帶選取，對選出的子頻帶降噪后重構(gòu)信號,再使用Teager能量算子對重構(gòu)信號解調(diào)，對解調(diào)后的信號進行頻譜分析得到故障特征頻率，實現(xiàn)故障診斷。將該方法分別應(yīng)用于仿真故障信號與實測信號，驗證了該方法的有效性。

1 理論介紹

1.1 TQWT可調(diào)Q因子小波變換基本理論

TQWT是在離散二進小波變換基礎(chǔ)上改進的可以靈活調(diào)節(jié)Q因子的離散小波變換。與經(jīng)典小波變換不同，TQWT直接在頻域上利用小波基的頻域響應(yīng)對被處理信號進行濾波。在頻域上設(shè)計雙通道過采樣濾波器組，將信號分解為高頻部分和低頻部分，經(jīng)過尺度變換后，高頻部分作為本層輸出，低頻部分作為下層的輸入繼續(xù)分解。這樣通過高、低通濾波器組的層層分解將信號分解為不同子頻帶,TQWT分解的信號具有可重構(gòu)性。具體分解過程如圖1所示，重構(gòu)即分解的逆向過程。

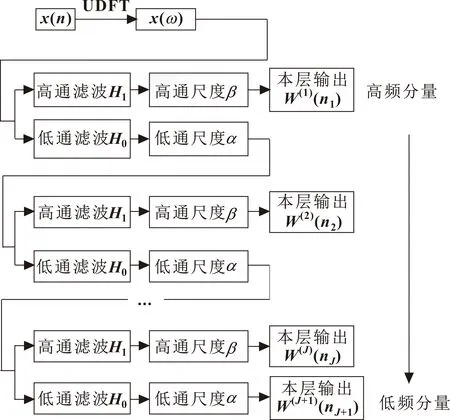
圖1 TQWT分解過程Fig.1 TQWT decomposition process

圖1中每一層的輸出W為TQWT分解的小波系數(shù)序列，可單支重構(gòu)為子頻帶時間序列。定義第j層子頻帶的中心頻率為fc,帶寬為Bw[10]，計算公式分別為

(1)

式中:fs為采樣頻率;α、β分別為濾波器的高通變換尺度和低通變換尺度，定義為

(2)

式中:Q為小波的品質(zhì)因子，Q越大，小波時域振蕩次數(shù)越多；r是冗余系數(shù)，表現(xiàn)為分解所得子頻帶的重合度；J是最大分解層數(shù)，影響低頻段分解性能，分解完成后會獲得J+1個子頻帶。三參數(shù)(Q,r,J)共同定義了TQWT的性質(zhì)和特性。最大分解層數(shù)J可以由Q、r確定，表達式為

(3)

式中：?·」為向正無窮取整；N為原信號長度。

1.2 Teager能量算子

20世紀(jì)80年代，TEAGER等提出一種非線性算子TEO(Teager Energy Operator)，又被稱為Teager能量算子，最初被應(yīng)用在聲音信號增強建模上。連續(xù)信號x(t)的能量算子ψc定義如下:

(4)

ψ[x(n)]=x2(n-1)-x(n)x(n-2)

(5)

對于某個具有時變幅值和時變相位的聲發(fā)射傳感器響應(yīng)信號h(t)[11]：

h(t)=exp(-2πξfnt)sin(2πfnt)

(6)

式中：fn為傳感器固有頻率；ξ是阻尼系數(shù)。使用Teager能量算子對其處理得：

ψc[h(t)]=[exp(-2πξfnt)]2·(2πfn)2

(7)

由公式(7)可知:Teager能量算子能很好地對原始信號進行解調(diào)，相比信號能量定義為幅值的平方，Teager能量算子增加了瞬時頻率平方的乘積[12]。對于軸承故障聲發(fā)射信號這種高頻沖擊信號，Teager能量算子可以有效增強故障特性。

另一方面，Teager能量算子對噪聲十分敏感，因此常將其與其他方法結(jié)合以減弱噪聲的影響[13]。

2 多指標(biāo)優(yōu)化的TQWT方法

為了從軸承早期故障聲發(fā)射信號提取出微弱故障特征，提出一種多指標(biāo)優(yōu)化的TQWT方法。該方法可以對原始信號進行自適應(yīng)分解，并篩選出包含故障信息的子頻帶進行降噪和重構(gòu)，有利于提高后續(xù)能量算子解調(diào)效果。

2.1 參數(shù)范圍確定

根據(jù)公式(3)可知，最大分解層數(shù)J可由Q、r確定；根據(jù)TQWT基本性質(zhì)可知，Q的取值不小于1，同時為了防止Q過大導(dǎo)致小波共振屬性過高產(chǎn)生奇異信號，將Q的取值范圍設(shè)為[1,20]；綜合考慮計算量和實際需要，將r的取值設(shè)為3[14-15]。

2.2 參數(shù)自適應(yīng)選擇

TQWT參數(shù)的選取可以視為設(shè)計中心頻率和帶寬不同的濾波器組，通過這些濾波器得到一系列子頻帶。研究表明聲發(fā)射信號的波形熵可以作為故障特征指標(biāo)，子頻帶波形信息熵越小，說明該頻帶中含有越多故障成分[16]。峭度是常用的描述信號沖擊成分指標(biāo)，峭度越大信號中的沖擊性成分越多。對于長度為N的序列{x(n)},峭度的公式為

(8)

式中：σ為序列標(biāo)準(zhǔn)差；u為平均值。結(jié)合峭度指標(biāo)與波形熵指標(biāo)，使子頻帶峭度最大化的同時使波形熵盡可能小。對于選定的參數(shù)(Q,r)，分解得到J+1個子頻帶，其中第j層子頻帶對應(yīng)改進峭度波形熵比Cj定義為

(9)

式中：xij為第j層子頻帶的第i個元素；N為子頻帶序列長度；Kj表示第j層子頻帶峭度。取所有子頻帶峭度波形熵比中的最大值C為參數(shù)(Q,r)定義下的故障特征指標(biāo)。在給定范圍內(nèi)遍歷參數(shù)的取值，C取到最大值時，對應(yīng)參數(shù)為最佳分解參數(shù)。

2.3 子頻帶選擇和降噪

分解完成后得到J+1個子頻帶，由于聲發(fā)射信號頻帶寬，具有多頻率解調(diào)特性，為了獲得相對完整的故障信息并去除噪聲，將3種故障特征融合為一個新的故障特征指標(biāo)對子頻帶進行篩選。為了使前后優(yōu)化方向一致，選用峭度作為故障指標(biāo)之一，峭度雖然對沖擊敏感但是容易受到局部極值影響，峰度系數(shù)可以反映信號整體波形的極端程度，不易受局部極點影響。峰度系數(shù)M表示為

(10)

稀疏值S可以表示信號的故障稀疏程度，為

(11)

分別求每個子頻帶信號的峭度K、峰度M、稀疏度S，得到3個特征指標(biāo)序列{K(i)}、{M(i)}、{S(i)},使用這3個序列構(gòu)成多指標(biāo)的狀態(tài)矩陣：

X=(xij)3×(J+1)=

(12)

式中：xij表示矩陣中第i行第j列元素。分別對矩陣中同一類指標(biāo)求信息熵：

(13)

式中：Ei存在一個最大值ln(J+1)。信息熵小的指標(biāo)會給出更有價值的故障信息,因此在特征融合過程中給信息熵小的指標(biāo)更大權(quán)重[17-18]。為了消除不同指標(biāo)間的差異，將各子帶的3個指標(biāo)采用min-max標(biāo)準(zhǔn)化后根據(jù)信息熵的大小對其賦予不同的權(quán)重，計算得到每個子頻帶的融合特征參數(shù)。

(14)

(15)

(16)

式中：Wi表示各特征指標(biāo)的權(quán)重；Fj為各子頻帶的融合特征指標(biāo)。求出Fj的平均值，將Fj值大于平均值2倍的子頻帶挑選出來，對這些分量采用無偏似然估計軟閾值去噪，之后使用去噪后的分量重構(gòu)信號。設(shè)序列為x(t)，序列長度為n，閾值σ的具體計算方式為

(17)

(18)

3 故障診斷總流程

提出的多指標(biāo)優(yōu)化TQWT與Teager能量算子結(jié)合的故障診斷方法具體步驟如下：

(1)使用峭度波形熵比優(yōu)化的自適應(yīng)TQWT算法對故障信號進行分解,得到多個子頻帶。

(2)根據(jù)融合特征指標(biāo)選出包含故障特征成分的子頻帶，對其降噪后重構(gòu)信號。

(3)使用Teager能量算子對重構(gòu)信號解調(diào)，得到解調(diào)譜，從解調(diào)譜中得到故障特征頻率，實現(xiàn)特征提取和故障診斷。

4 仿真信號檢驗

軸承外圈故障聲發(fā)射信號可描述為近似周期性雙沖擊響應(yīng)，公式如下：

(19)

式中：x(t)表示滾動軸承故障產(chǎn)生的聲發(fā)射信號；x1(t)表示第一個沖擊響應(yīng)；x2(t)表示第二個沖擊響應(yīng)；ε(t)表示噪聲；h(t)由公式(6)確定，式中ξ取0.05，fn取3 kHz；采樣速率設(shè)定為20 kHz，采樣時間1 s，并對其加入高斯白噪聲使得信噪比為-13 dB。原始仿真信號時域波形如圖2(a)所示，加入噪聲仿真信號如圖2(b)所示。對加入噪聲的仿真信號進行頻譜分析，低頻段如圖2(c)所示，可以看出信號已經(jīng)完全被噪聲淹沒，從頻譜圖上也無法得到明顯故障信息。

圖2 仿真信號時頻圖

使用文中的方法對信號進行處理，根據(jù)前文確定的品質(zhì)因子Q變化為[1,20], 冗余系數(shù)r取3,搜索步長為1，在范圍內(nèi)搜索使得C最大的Q值。C隨Q變化情況如圖3所示,在Q=8時C取到最大值1.116 2，分解得到83個子頻帶。根據(jù)融合特征指標(biāo)下對子頻帶進行篩選，圖4列出了所有子頻帶對應(yīng)的融合特征值。

圖3 C隨Q變化情況(仿真數(shù)據(jù))Fig.3 Case that C changes with Q(simulation signal)

圖4 子頻帶篩選標(biāo)準(zhǔn)(仿真數(shù)據(jù))Fig.4 Sub-bands screening criteria(simulation signal)

融合特征值的平均值為0.003 1，選出特征值大于平均值2倍的子頻帶，j=15、16的子頻帶滿足條件。對選出的子頻帶降噪后重構(gòu)信號如圖5所示，使用Teager能量算子對重構(gòu)后的信號進行解調(diào)得到能量算子序列如圖6所示，對能量算子序列做頻譜分析，得到圖7所示低頻段的頻譜圖，可以清楚看到故障特征頻率及其諧波，與設(shè)計的外圈故障頻率10 Hz符合，實現(xiàn)特征提取和故障診斷。

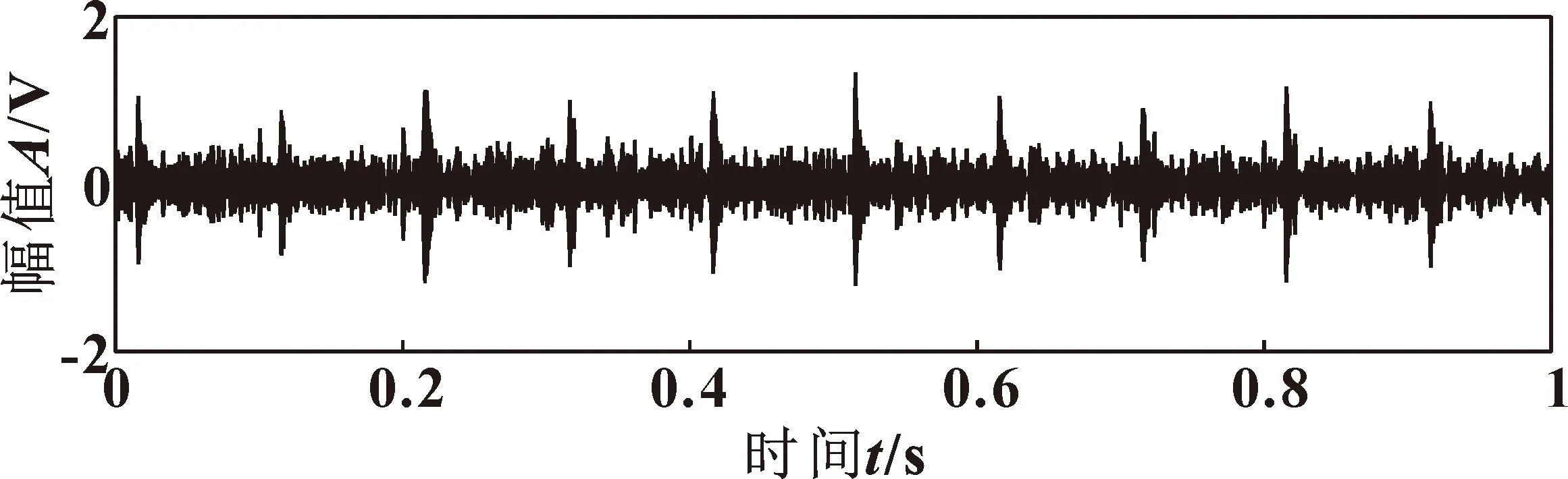
圖5 去噪后的重構(gòu)信號Fig.5 Reconstructed signal after denoising

圖6 重構(gòu)信號Teager能量算子序列Fig.6 Reconstructed signal Teager energy operator sequence

圖7 低頻段Teager能量算子頻譜Fig.7 Teager energy operator spectrum in low-frequency stage

5 軸承故障診斷實驗

5.1 實驗說明

為了進一步證明方法的有效性，設(shè)計實驗進行驗證。實驗軸承為N205深溝球軸承，軸承節(jié)徑為38.5 mm，滾動體直徑6.5 mm，滾動體個數(shù)為13，接觸角為0°，在滾動體上設(shè)置了寬度約0.4 mm、深度約0.5 mm的裂紋缺陷。實驗設(shè)備為QPZZ-II故障診斷模擬實驗平臺，試驗臺如圖8所示。

圖8 故障診斷模擬實驗平臺Fig.8 Fault diagnosis simulated experimental platform

實驗時將聲發(fā)射傳感器置于軸承上方，以1 MHz的采樣頻率對聲發(fā)射故障信號采樣，每次采樣131 072個點，電機轉(zhuǎn)速為600 r/min，對應(yīng)轉(zhuǎn)頻10 Hz。

5.2 滾動體故障信號分析

經(jīng)過計算得滾動體故障頻率fOR=57.5 Hz，為了模擬工業(yè)環(huán)境中的強噪聲環(huán)境，不對原信號做硬件濾波處理，并利用軟件向原信號加入5 dB白噪聲，所得信號時域波形如圖9(a)所示。可以看出信號存在沖擊干擾而且故障成分被噪聲淹沒。對其進行頻譜分析，低頻段頻譜如圖9(b)所示，無法通過該頻譜分辨故障特征。

圖9 強噪聲背景下滾動體故障信號時頻圖

采用文中的方法對其進行處理。首先使用自適應(yīng)TQWT對信號進行分解，C隨品質(zhì)因子Q變化情況如圖10所示。

圖10 C隨Q變化情況(實驗數(shù)據(jù))Fig.10 Case that C changes with Q(test signal)

最優(yōu)分解參數(shù)Q=3時，Cmax=4.123 3，計算出J=49。分解得到50個子頻帶，子頻帶對應(yīng)的融合特征參數(shù)如圖11所示。

圖11 子頻帶篩選標(biāo)準(zhǔn)(實驗數(shù)據(jù))Fig.11 Sub-bands screening criteria(test signal)

經(jīng)計算融合特征參數(shù)平均值為0.024 9，大于兩倍平均值的子頻帶有j=25、26、27、28、29、30、32。對選出的子頻帶進行無偏似然軟閾值去噪后重構(gòu)信號，重構(gòu)信號如圖12所示。

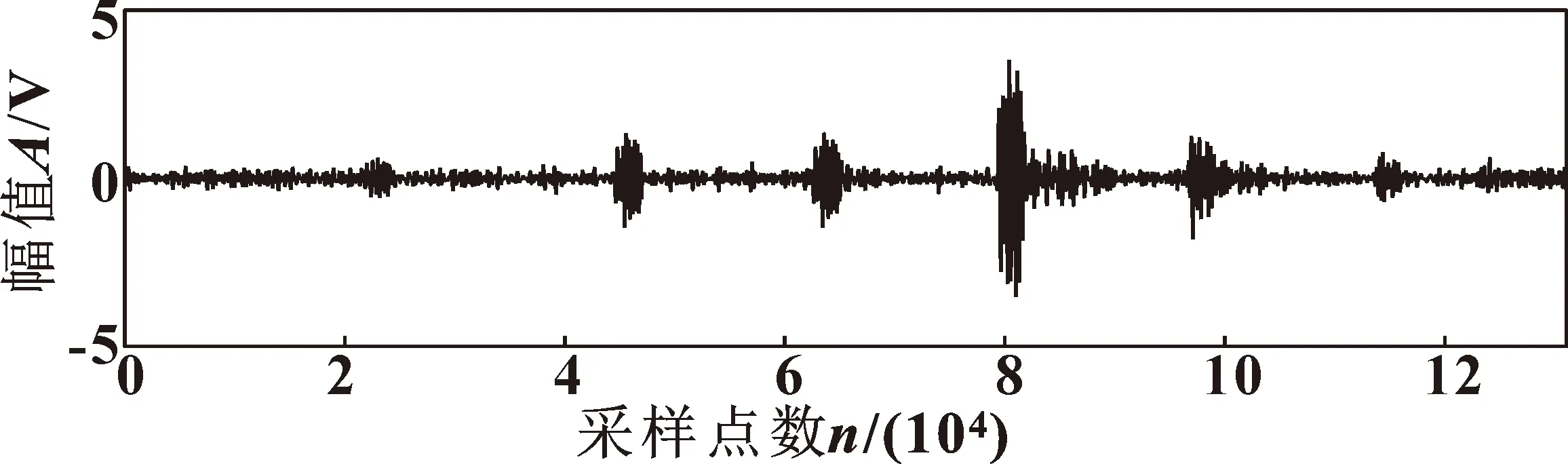
圖12 重構(gòu)信號Fig.12 Reconstructed signal

使用Teager能量算子對重構(gòu)后的信號進行處理得到能量算子序列，并進行頻譜分析，結(jié)果如圖13所示。

圖13 Teager能量算子序列(a)與頻譜(b)Fig.13 Teager energy operator sequence(a) and spectrum(b)

對Teager能量算子頻譜進行分析，發(fā)現(xiàn)第一個峰值對應(yīng)的頻率為10 Hz，與電機轉(zhuǎn)頻符合，之后的峰值出現(xiàn)在61 Hz及其倍頻附近。考慮到電機運行過程中的轉(zhuǎn)速波動與滾動體打滑等因素影響，提取出的峰值頻率與計算所得滾動體fOR=57.5 Hz是符合的，成功提取出滾動體故障特征并實現(xiàn)故障診斷。

5.3 與現(xiàn)有方法對比分析

現(xiàn)有的改進TQWT方法往往只使用了一種特征指標(biāo)對TQWT進行優(yōu)化，如文獻[5]使用了能量熵作為優(yōu)化指標(biāo)，文獻[6-7]使用了峭度作為優(yōu)化指標(biāo)。使用單一指標(biāo)往往存在局限性而且在工程中魯棒性不強。而且現(xiàn)有的方法都是對振動信號進行處理，只選取出所有子頻帶中唯一的最優(yōu)子頻帶，由于聲發(fā)射信號具有多頻帶解調(diào)特性，僅選取單一頻帶會導(dǎo)致大量故障信息被遺漏。

以上文處理的滾動體故障信號為例，僅使用峭度指標(biāo)對TQWT參數(shù)進行優(yōu)化并選取最優(yōu)子頻帶，所得最優(yōu)分解參數(shù)Q=5，選出的解調(diào)頻帶僅有j=27子頻帶，重構(gòu)所得信號如圖14所示。可以明顯看出圖14中的故障沖擊比圖12中的微弱。對其進行能量算子解調(diào)后進行頻譜分析，如圖15所示。該頻譜中的峰值與圖13(b)相比不夠明顯，特征頻率的倍頻處峰值也較少。

圖14 對比重構(gòu)信號Fig.14 Contrasted reconstructed signal

圖15 對比能量算子頻譜Fig.15 Contrasted energy operator frequency spectrum

以上對比分析表明文中的方法在滾動軸承早期故障聲發(fā)射信號的處理上有更好的適用性和優(yōu)越性，具有一定的工程應(yīng)用價值。

6 結(jié)論

(1)以最大化子頻帶峭度波形熵比作為TQWT分解的參數(shù)優(yōu)化目標(biāo)，充分考慮故障的沖擊特性和聲發(fā)射信號的波形特性，解決了TQWT參數(shù)選取問題，提高了信號分解效果。

(2)針對聲發(fā)射信號的多頻帶解調(diào)特性，使用信息熵對峭度、峰度、稀疏度加權(quán)歸一化融合為新特征指標(biāo)。通過該指標(biāo)對解調(diào)頻帶進行選擇，有效避免了單一指標(biāo)的局限性，使頻帶選擇更準(zhǔn)確合理。

(3)Teager能量算子可以增強信號的沖擊特征并解調(diào)，但是對噪聲敏感，因此將其與改進的TQWT結(jié)合。仿真和實驗結(jié)果表明：該方法能在強噪聲背景下提取軸承早期故障聲發(fā)射信號中的微弱故障成分，實現(xiàn)故障診斷。