基于高速開關閥的調節閥定位系統建模研究

袁豪揚，班 偉，劉璐璐，賈 華

(1.寧夏大學機械工程學院，寧夏 銀川 750021；2.寧夏吳忠儀表責任有限公司，寧夏 吳忠 751100)

0 引言

在現代自動化工業生產中，調節閥是工業自動化的重要組成部分，被廣泛應用于電力、石油、化工、冶金等工業領域，主要對生產過程中流量、壓力、溫度等變量因素進行控制。隨著溫室效應的影響與生產需求的不斷提高，現代化工業生產面臨減少能源消耗與提高生產效率的要求，因此氣動調節閥的應用場景越來越復雜，生產過程中相關變量的控制精度要求也變得更為嚴苛。這就對高速調節閥的定位精度提出了更高的要求。

定位器是生產中廣泛應用的調節閥伺服定位元件。文獻[1]對閥門定位器位置反饋系統的精度分配和計算進行了全面的分析研究。文獻[2]、文獻[3]介紹了智能定位器的組成和工作原理，說明了智能定位器能夠很好地服務于工業生產。文獻[4]設計了1種氣動調節閥智能檢測系統。我國在工業控制領域起步較晚，定位器主要依賴國外品牌的成套設備[5]。為了提高定位器的性能，國內學者作了不少研究。但國內定位器的高端市場依舊被國外品牌壟斷。因此，研究1種不依賴閥門定位器也能實現對調節閥精密定位的控制方案顯得尤為重要。

文獻[6]提出了氣動過程控制閥的非線性模型，并通過試驗評估模型的性能。文獻[7]、文獻[8]分別使用參數估計和試驗辨識的方法獲取系統中的重要參數，并憑借這些參數完成了對系統模型的精確建模。文獻[9]通過對氣動伺服閥進行開環調試,從而驗證數學模型的可靠性、準確性,并對理論模型進行參數修正。參數估計的優劣決定了模型解釋實際問題的可信度。參數的不確定性會導致建立的數學模型與系統的實際特性有較大的偏差。因此，獲取參數是建模過程中必不可少的關鍵環節。

本文提出了1種由高速開關閥、膜片式高參數調節閥和數字控制器構成的伺服定位系統。本文首先對伺服定位系統各個組成部分進行理論分析，建立了數學模型；然后通過間接測量的方式對系統最大靜摩擦力、滑動摩擦力以及泄露面積等參數進行求解；最后通過試驗結果與仿真結果的對比，驗證數學模型的準確性。

1 系統模型

本文所提伺服定位系統主要由膜片式高參數調節閥、高速開關閥、閥位變送器、快速開發控制原型系統組成。圖1為系統方案簡圖。

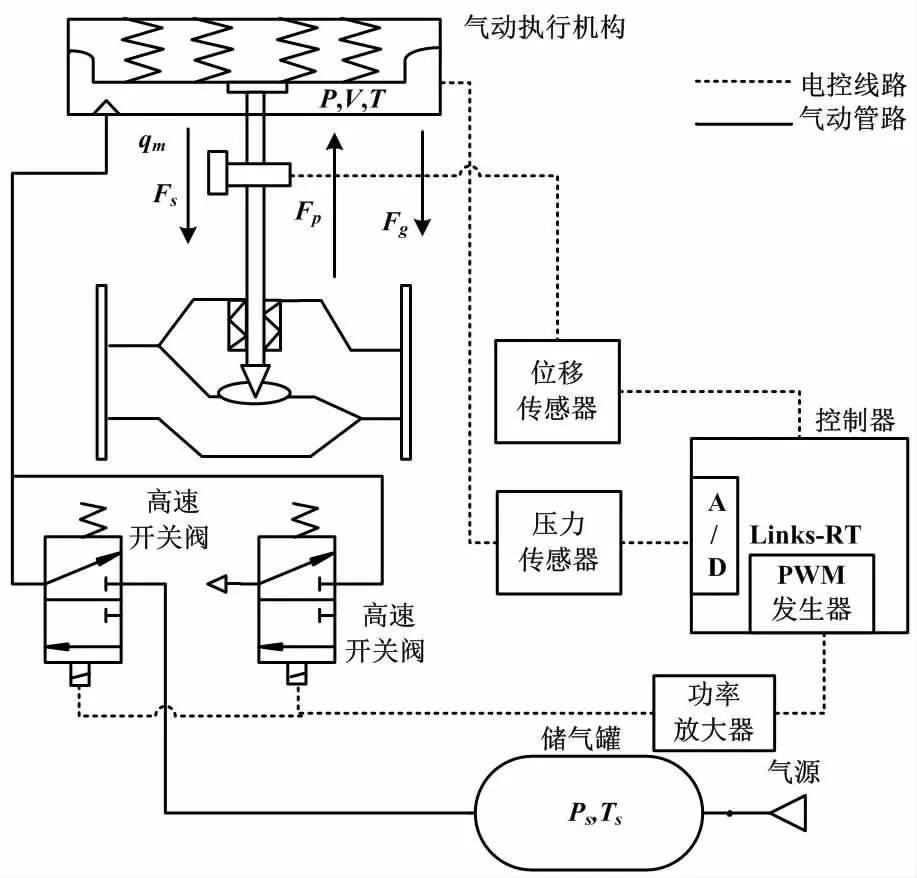
圖1 系統方案簡圖Fig.1 System solution sketch

為簡化推導，對圖1所示系統作如下假設：①系統工作介質為理想氣體，滿足理想氣體狀態方程；②氣源壓力Ps和溫度Ts恒定；③氣動薄膜執行機構氣室中氣體是均勻的，氣室中各個時刻的各個方位參數相等；④氣體在流過閥口或其他節流孔時的流動狀態均為等熵絕熱過程。

1.1 高速開關閥數學模型

高速開關閥閥口開口面積與閥芯位移成正比。為了控制需要，本文更關注1個脈沖寬度調制(pluse width modulation，PWM)周期內開關閥閥口的平均有效面積，而不是其閥口截面積的瞬時值。在PWM周期內， 高速開關閥閥口有效面積可以表示為[10]：

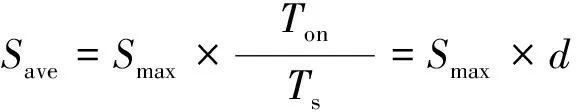
(1)

式中：Smax為閥口最大有效面積，m2;d為PWM信號的占空比，%。

國際標準ISO/6358規定，氣動元件流量特性由2個特征參數描述：臨界壓力比b和聲速流導C[11]。但是標準所給定的測試方法對測量精度要求極為苛刻，一般情況下很難保證所測量的2個特征參數足夠精確，且這種測量方法耗氣量很大。因此，本文采用的2個特征參數是臨界壓力比b和有效截面積S。氣體質量流量方程為：

(2)

式中:P為閥口外壓力，Pa；Ps為氣源壓力，Pa，Ts為氣源溫度，K；b為臨界壓力比,取值0.528。

1.2 氣室熱力學方程

氣室內的質量變化率等于流入質量流量減去流出質量流量:

(3)

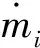
即:

(4)

(5)

薄膜氣室壓力隨物質流量的變換關系為：

(6)

1.3 閥桿動力學模型

在理想狀態下，視執行機構閥桿為理想剛體，即在無明顯外力作用下閥桿不會發生形變，且彈簧在解除外力的情況下仍能夠有良好的恢復性。閥桿的運動力學方程為：

(7)

式中:m為閥桿質量，kg；Fp為薄膜作用力，N；Fs為彈簧作用力，N；Ff為摩擦力，N；Fvc為閥桿的不平衡力，N。

①薄膜作用力。

供氣壓力作用在薄膜上，產生向上的薄膜作用力為：

Fp=Pe×Ae

(8)

式中：Pe為氣室壓力，Pa；Ae為薄膜有效面積，m2。

②彈簧反作用力。

由于薄膜反作用力較小，為了建模方便可對其忽略不計。假設閥桿位移x與彈簧呈線性，薄膜的彈力Fs可表示為:

Fs=Ks×(x+x0)

(9)

式中：Ks為彈性系數，N/m；x為閥桿位移，m；x0為彈簧預緊量，m。

③閥桿的摩擦力。

(10)

式中：Kd為粘滯系數；l為庫倫摩擦力，N；v為閥桿速度，m/s；Fp為施加的合外力，N；fmax為最大靜摩擦力，N。

1.4 仿真模型

本文基于Simulink建立高速開關閥控位置系統仿真模型。氣動伺服系統模型如圖2所示。

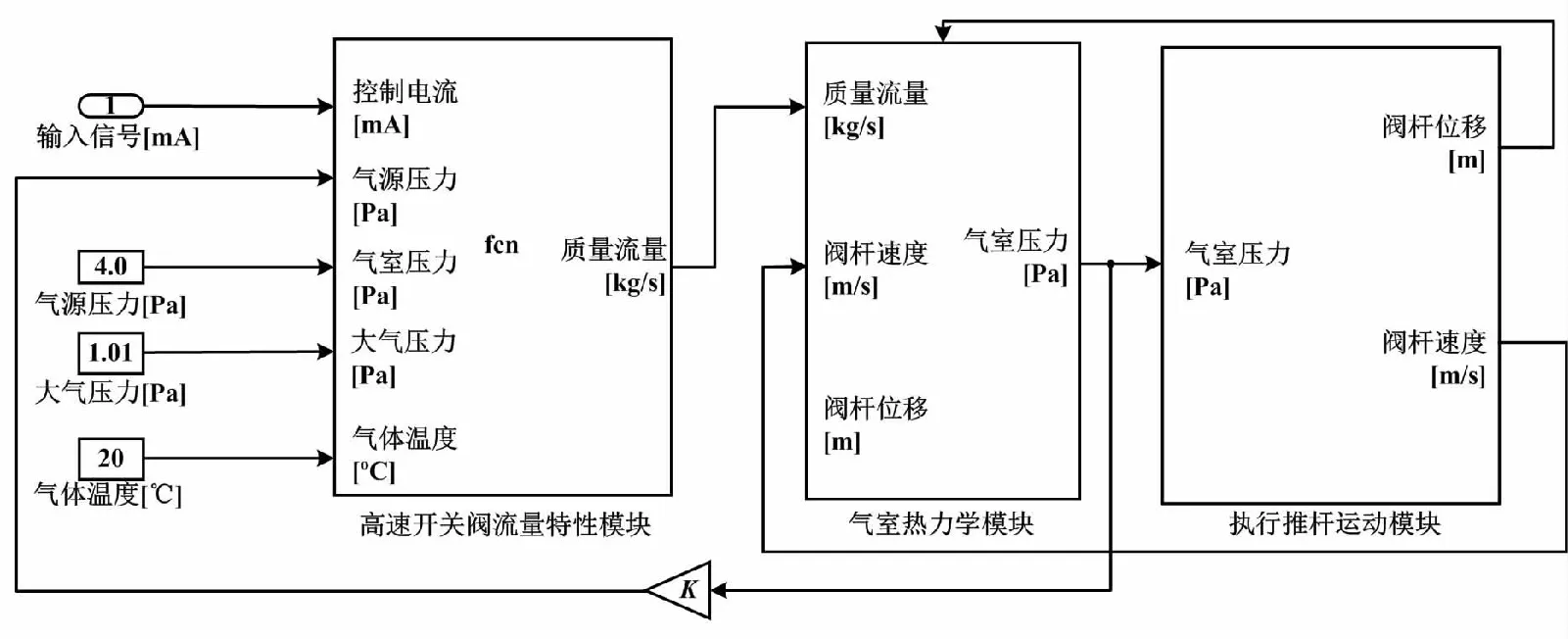
圖2 氣動伺服系統模型 Fig 2 Pneumatic servo system model

本文根據式(6)建立氣室容腔壓力微分方程的模型。氣室熱力學模型如圖 3所示。

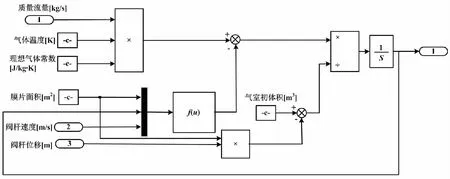
圖3 氣室熱力學模型 Fig 3 Thermodynamic model of gas chamber

本文根據式(7)構建執行機構運動模型。執行機構運動模型如圖 4所示。

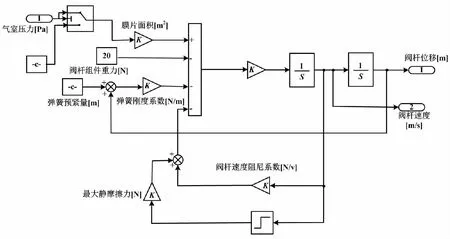
圖4 執行機構運動模型Fig.4 Actuator motion model

2 模型參數

模型中常量仿真參數如下。執行推桿組件質量m為2 kg;執行機構膜片面積Ae為3.2×10-2m2;閥口最大有效面積Smax為1.8×10-6m2;執行機構行程L為16 mm;執行機構氣室初體積V0為1.1×103cm3;執行機構彈簧剛度Ks為2.33×105N/m;氣體常數R為287 N·m/(kg·K);環境溫度T為20 ℃；執行機構彈簧預緊力F0為4.5 KN；氣源壓力Ps為5×105Pa。

研究對象的有些參數是已知的，可通過查詢常用標準參數表或者直接讀表獲得，如氣體溫度、供氣壓力等。但仍有一些對系統特性影響較大的參數，如最大靜摩擦力、滑動摩擦力以及氣室的泄漏面積等參數無法通過上述方法獲得，只能通過試驗獲取。

2.1 最大靜摩擦力的測量

在進行氣動調節閥的安裝時，彈簧一般會進行適當的壓縮。這是彈簧產生一定的反作用力以保證氣動調節閥有一定的開關度。這種反作用力被稱為彈簧的預緊力。其表達式為:

F0=P0Ae=ksx0

(11)

式中：P0為克服彈簧預緊力所需要的氣壓值，Pa。

假設閥桿將要移動的瞬間，閥桿速度為零、加速度為零，即合力為零。此時，閥桿處于力平衡狀態，表達式為:

P1Ae-mg-ks(x+x0)-fmax=0

(12)

式中：P1為閥桿移動瞬間氣室壓力，Pa；fmax為控制閥最大靜摩擦力，N。

所以，有：

fmax=P1Ae-mg-ks(x+x0)

(13)

最大靜摩擦力的測量曲線如圖5所示。

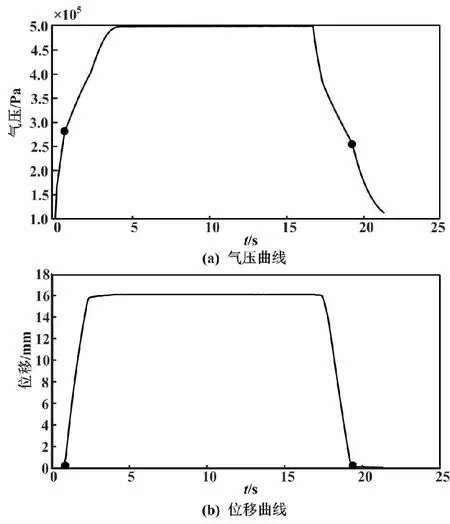
圖5 最大靜摩擦力的測量曲線Fig.5 Measurement curves of maximum static friction

給定高速開關閥1個固定占空比。2個高速開關閥以1個固定的占空比信號交替作用，使系統走完1個全程。壓力傳感器與位移傳感器采集整個過程中的閥位、氣室氣壓的數據。將閥桿的將要變化和不再變化時的氣壓值代入式(13)，即可獲得控制閥的最大靜摩擦力。

本文設m=2 kg、F0=4.5 kN、Ks=2.336 75×105N/m、Ae=0.032 m2、x=0、P=2.759×105Pa。將上述值代入式(13)，計算得fmax=4 308.8 N。

為了驗證上述測量方法的可靠度，在本次測試中隨機抽取5個不同占空比，并記錄下它們的氣壓值，通過計算獲得動摩擦力的大小。不同占空比下氣壓值如表1所示。

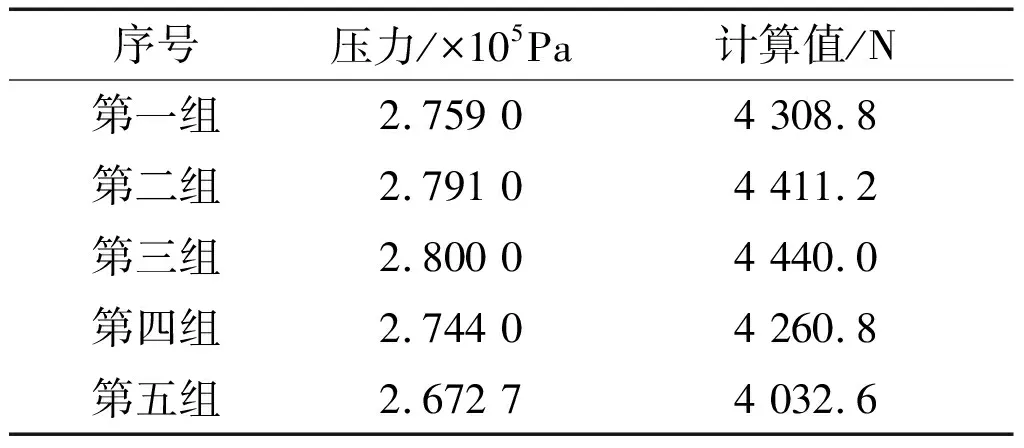
表1 不同占空比下氣壓值

上述5組數據的平均計算值為4 290.7 N，則最大靜摩擦力平均值為4 290.7 N。

2.2 滑動摩擦力的測量

當閥桿處于運動狀態時，閥桿受到滑動摩擦力的作用，一般認為物體在低速度時滑動摩擦力的大小與速度大小成反比。這種現象被稱為Stribeck[12]現象。雖然這種摩擦力模型可以更加準確地描述閥桿在運動中所受的滑動摩擦力，但測量數據的變化較小，要求設備的精密度較高，本次試驗設備無法做到如此精密的測量。因此，可以將其視為1個常量，根據牛頓第二定律來計算：

(14)

當閥桿保持勻速運動，則閥桿的加速度為0，即閥桿所受合力為0。因此，閥桿的滑動摩擦力等于其他力的合力，表達式為:

(15)

式中：Pa、Pb為某一時刻的氣室氣壓值,Pa。

若給定系統1個激勵信號，使閥桿保持勻速運動，當閥桿到達終點位置后再給1個反向的激勵信號，使閥桿保持同樣的速度反向運動。假設閥桿在進行往復運動時經過同1個閥位點x，閥桿正向運動經過閥位x時的摩擦力為Fa，閥桿反向運動經過閥位x時的摩擦力為Fb。由于閥桿作勻速運動，所以閥桿在作往復運動時經過同1個閥位點的滑動摩擦力大小不變，方向相反。其表達式為:

(16)

給定系統1個激勵信號，使閥桿保持勻速運動，當閥桿位移達到最大值時，給定系統1個反向激勵信號，使閥桿作反向勻速運動。壓力傳感器與位移傳感器分別采集整個運動過程中的壓力信號與位移信號。在上述采集數據中找到經過同1個閥位x時的2個氣室氣壓值，并將其代入式(16)，從而計算獲得控制閥的滑動摩擦力。

滑動摩擦力的測量曲線如圖6所示。

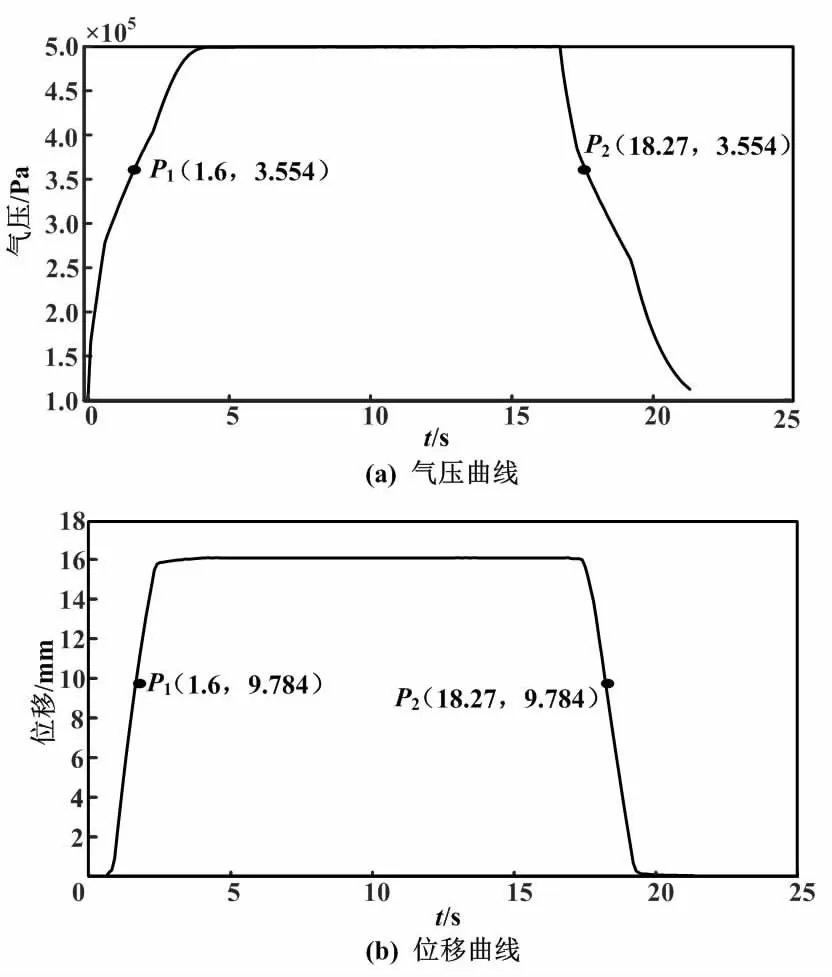
圖6 滑動摩擦力的測量曲線Fig.6 Sliding friction measurement curves

由圖6可知，閥桿運動時的閥位曲線為一條直線。這表示閥桿一直在作勻速運動。左側斜率為9.138 25，右側斜率為-8.121 66，數值的絕對值相差不大，近似為閥桿正反向運動速度相等。

為了驗證上述測量方法的可靠度，在本次測試中隨機抽取5個不同閥位點，并記錄下它們的氣壓值，通過計算獲得滑動摩擦力的大小。不同閥位的氣壓值如表2所示。

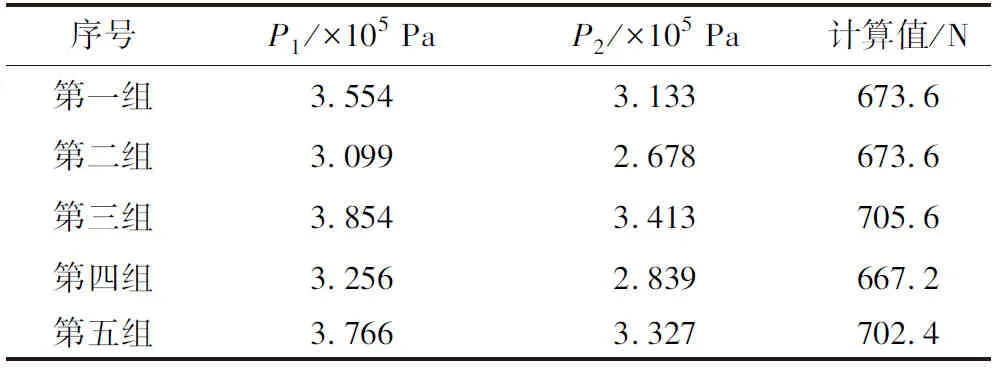
表2 不同閥位的氣壓值

上述5組數據的平均計算值為684.5 N。因此，滑動摩擦力的平均值為684.5 N。

2.3 系統泄漏面積的測量

在進行理論推導時，一般默認系統密封性良好，但實際工作時管網及用氣設備中會發生泄漏。這一現象的產生會影響系統的穩定性。

當高速開關閥占空比減小到一定程度時，系統中進氣量等于泄漏量。此時，系統會達到穩定狀態。將系統泄漏近似為1個泄漏點，則泄漏面積可以通過氣體質量流量方程來計算：

(17)

通過設定高速開關閥占空比為20%，給定系統1個階躍信號，使閥桿緩慢移動至閥桿不能再移動為止。通過系統采集整個過程的閥位、氣室氣壓的變化值，找到氣室氣壓的最大值并記錄下來，代入式(17)得到系統泄漏面積。泄漏面積的測量曲線如圖7所示。

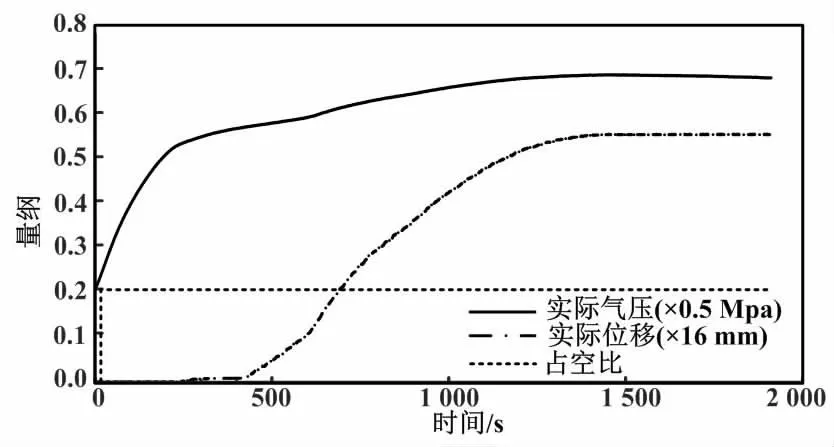
圖7 泄漏面積的測量曲線Fig.7 Measurement curves of leakage area

當高速開關閥占空比為20%時，系統在1 400 s時達到動態平衡。此時，氣室氣壓為340 200 Pa、閥桿位移為8.9 mm。在閥桿位置穩定時，系統內流入氣體質量流量等于流出氣體質量流量，室外壓強為101 000 Pa,由式(17)可計算出系統泄漏面積S=2.022 6×10-7m2。

2.4 PWM頻率的確定

當開關閥閥口的上下游壓力恒定時，可以通過改變PWM的頻率或占空比來對比說明占空比和PWM頻率對氣體質量流量的影響。圖8是不同占空比下的氣體流量與PWM頻率關系。

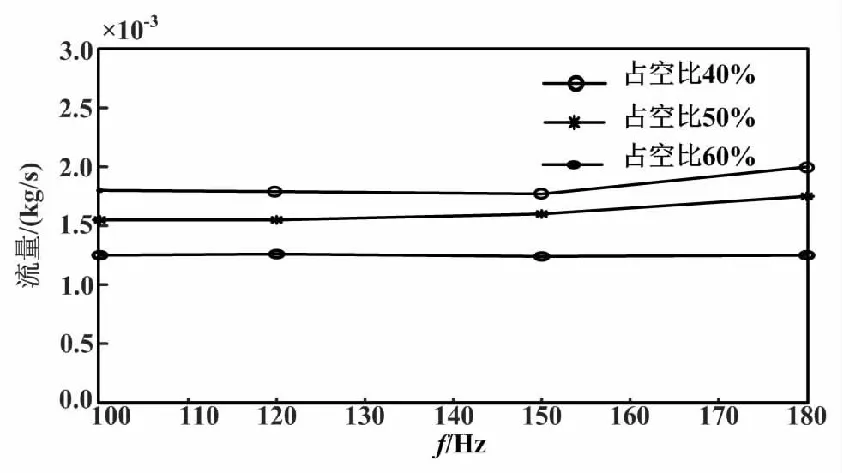
圖8 氣體流量與PWM頻率關系Fig.8 Gas flow rate versus PWM frequency relationship

由圖8可知，PWM 基頻在100～180 Hz 范圍內，當占空比相同時，頻率f的增大會使氣體流量增大，且占空比越小受到頻率變化的影響越小。因此，本次試驗可選擇PWM頻率為120 Hz。

3 模型驗證

為了驗證模型的正確性，本文根據工作原理，搭建了高速開關閥的實物測試平臺。試驗系統主要由閥位變送器、膜片式高參數調節閥、功率放大器、高速開關閥、電源、上位機、Links-box仿真機等組成。為降低信號干擾，用不同電源分別為閥位變送器、功率放大器供電。數據采集卡有12路PWM輸出、8路A/D輸入、4路D/A輸出、6路DI、6路DO、1路正交編碼器采集通道、1路CAN總線接口、1路RS232接口、 6路數字I/O線。本文僅使用定位器的閥位變送器作為位移傳感器進行試驗測試。試驗給系統1個脈沖信號。充氣端高速開關閥打開。放氣端高速開關閥保持關閉。氣源向調節閥氣室充氣使氣室壓力上升。膜片推動閥桿產生移動，然后通過閥位變送器采集閥桿位移數據。

3.1 高速開關閥流量模型的驗證

固定 PWM 頻率f=120 Hz，改變占空比和開關閥下游壓力，測出通過閥口的氣體流量 。圖9是質量流量與壓力比關系。圖9中，不同的曲線代表不同占空比。

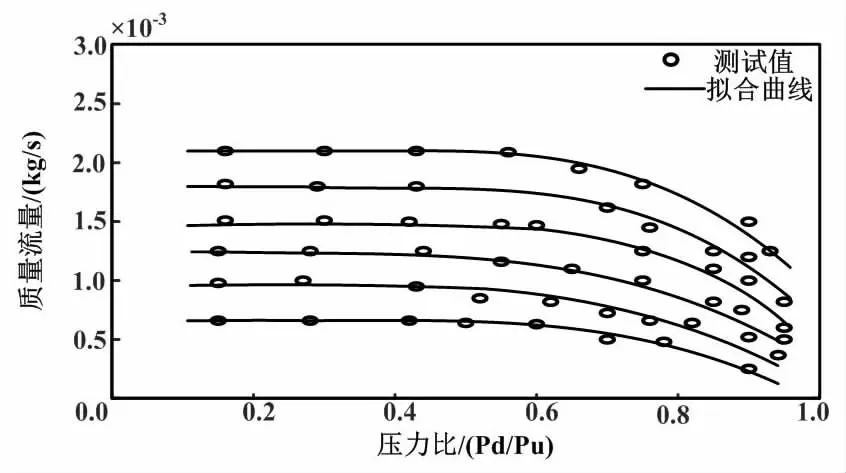
圖9 質量流量與壓力比關系Fig.9 Mass flow to pressure ratio relationship

由圖9可知，測試值和理論擬合曲線比較接近。因此，式(2) 能夠準確描述高速開關閥的數學模型，可以用來進行氣動開關伺服控制系統的設計，滿足實際應用的需要。

3.2 系統模型的驗證

50%占空比下的響應如圖10所示。

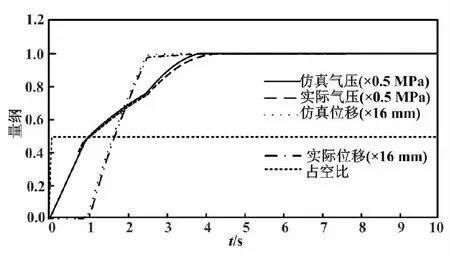
圖10 50%占空比下的響應Fig.10 Responses at 50% duty cycle

80%占空比下的響應如圖11所示。

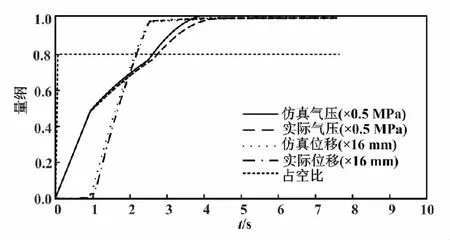
圖11 80%占空比下的響應Fig.11 Responses at 80% duty cycle

100%占空比下的響應如圖12所示。

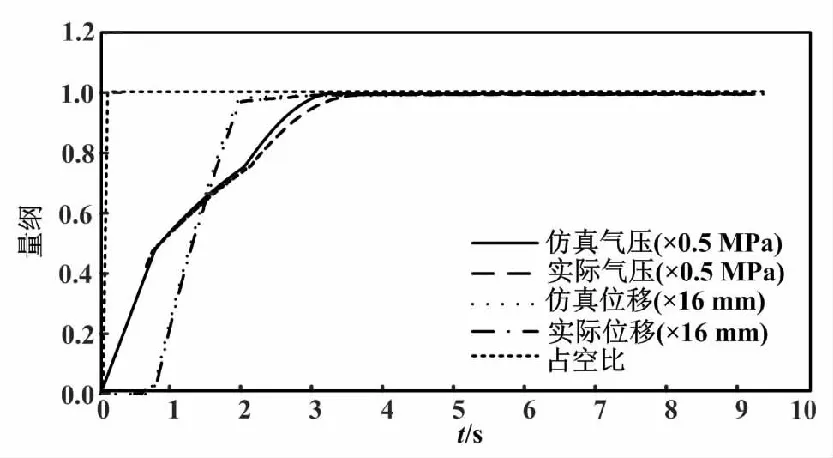
圖12 100%占空比下的響應Fig.12 Responses at 100% duty cycle

系統運行中，氣室壓強變化分為3個階段。第一階段是氣室壓強小于推動閥桿運動的最小壓強。在此階段內薄膜產生的推力不足以克服系統阻力而推動閥桿移動。第二階段是氣室壓強大于等于推動閥桿運動的最小壓強。在此階段內薄膜產生的推力推動閥桿移動。第三階段則是閥桿移動到限定位置，氣室體積不再變化，氣室氣壓小于等于氣源氣壓，氣室氣壓發生變化。隨著占空比的增大，系統的氣壓變化曲線差異變小。

通過對比位移的仿真曲線和試驗結果曲線，發現兩者之間變化趨勢相同。這驗證了系統數學模型的準確性。試驗結果曲線的斜率低于仿真曲線，是因為建立的系統數學模型采用了部分簡化和假設，沒有考慮實際閥口流量增益的非線性和氣室的熱量交換等因素，導致系統的數學模型與實際情況存在一定的偏差。

從上述仿真和試驗結果分析可知，系統的數學模型存在一定誤差。導致模型誤差的原因有模型簡化、閥口流量增益的非線性、系統的不確定性、氣室熱量的交換等。實際上，氣動伺服控制系統本質是1個非線性不確定性系統。系統的不確定性包含參數不確定性和不確定性非線性。被控氣室熱力學過程的簡化、高速開關閥流量增益的變化等均稱為系統的參數不確定性。系統未建模動態和外界干擾信號等不能通過數學模型建立。這稱為系統的不確定性非線性。因此，在對高參數調節閥的精密定位問題進行研究時，這些因素都需納入考慮。

4 結論

本文對基于高速開關閥的精密定位系統進行了相關研究，旨在建立1個可以反映系統基本特性的數學模型。對于無法直接查詢獲取的系統參數可通過間接測量的方法來獲取，并通過試驗獲得系統的最大靜摩擦力、滑動摩擦力以及泄漏面積等參數。將系統參數代入數學模型便可進行仿真驗證，由仿真結果與真實試驗結果的吻合程度來說明模型的可靠性。仿真結果與真實試驗結果吻合較好,說明模型可用于控制器的設計與研究。模型驗證中，由于模型簡化、閥口流量增益的非線性、系統的不確定性、氣室熱量的交換等因素導致模型出現誤差。這些因素也是實現精密定位時所需考慮解決的問題。