基于非線性建模的水電機組動態(tài)特性仿真研究
魏加達,王衛(wèi)玉,張 培
(湖南五凌電力科技有限公司,湖南 長沙 410000)
1 引言
水輪機調(diào)節(jié)系統(tǒng)作為受水機電三大因素耦合作用的復(fù)雜非線性系統(tǒng),是保證水輪發(fā)電機組安全穩(wěn)定運行的重要控制設(shè)備[1]。搭建水輪機調(diào)節(jié)系統(tǒng)模型,進行仿真計算可為發(fā)電機組參數(shù)設(shè)計、導(dǎo)葉關(guān)閉規(guī)律整定、調(diào)速系統(tǒng)參數(shù)辨識以及模式切換等提供依據(jù),并將有利于改善大小波動過渡過程品質(zhì)以及一次調(diào)頻動態(tài)響應(yīng)特性等[2-4]。當前,一方面,大型機組突增突減負荷現(xiàn)象頻繁出現(xiàn),水電機組大波動過渡過程動態(tài)特性對電網(wǎng)安全穩(wěn)定的影響日益顯現(xiàn);另一方面,新能源建設(shè)的蓬勃發(fā)展、多類型電源互相協(xié)調(diào)的發(fā)展結(jié)構(gòu)對水電機組一次調(diào)頻性能提出了新的挑戰(zhàn),因此建立一個準確可行的數(shù)學(xué)模型對機組動態(tài)特性加以分析研究具有重大意義。由于水力因素的不穩(wěn)定性,特別是受水流慣性、流量時變性因素影響,以及水輪機功率調(diào)節(jié)非線性、發(fā)電機非線性特性以及電液隨動系統(tǒng)中主配壓閥輸出飽和非線性、主配壓閥死區(qū)非線性和主接力器速度限幅、主接力器輸出飽和非線性等眾多因素影響,使得想建立一個反映水輪機調(diào)節(jié)系統(tǒng)動態(tài)特性的精確數(shù)學(xué)模型變得極為復(fù)雜與困難,需研究者進行大量有針對性的細節(jié)研究與處理。此前,調(diào)節(jié)系統(tǒng)相關(guān)建模仿真應(yīng)用多為靜態(tài)特性研究、參數(shù)辨識等[5-8],缺乏對于機組動態(tài)特性的研究;在利用調(diào)節(jié)系統(tǒng)整體模型進行研究時,多采用理想水輪機模型與隨動系統(tǒng)一階模型[9-11],未針對隨動系統(tǒng)進行專門深入研究。本文綜合考慮調(diào)節(jié)系統(tǒng)各組成部分的非線性因素,建立了一個高精度反映調(diào)節(jié)系統(tǒng)真實動態(tài)特性的非線性模型。基于所建立的模型以大型水利樞紐TG 電站為例,進行了甩負荷大波動過渡過程與一次調(diào)頻動態(tài)響應(yīng)過程仿真,證明了文中所建立的非線性模型的能夠高精度、準確反映機組的甩負荷以及一次調(diào)頻動態(tài)特性,從而為機組甩負荷過渡過程品質(zhì)及一次調(diào)頻性能優(yōu)化研究提供了重要技術(shù)手段。
2 水輪機調(diào)節(jié)系統(tǒng)非線性建模
2.1 調(diào)節(jié)器模型
調(diào)節(jié)器數(shù)學(xué)模型的建立與其控制規(guī)律息息相關(guān),目前應(yīng)用廣泛的并聯(lián)PID 控制數(shù)學(xué)模型如圖1所示。
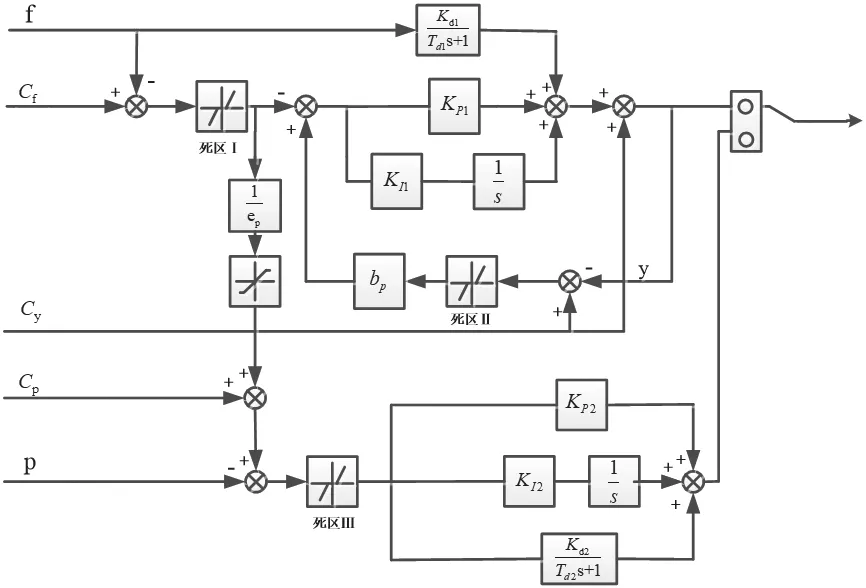
圖1 并聯(lián)PID 調(diào)速器控制邏輯框圖
圖1 中f為機組頻率;Cf為頻率給定;死區(qū)Ⅰ為頻率死區(qū);Cy為開度給定;KP1為開度模式下比例增益;KI1為開度模式下積分增益;Kd1為開度模式下微分增益;Td1為開度模式下微分衰減時間常數(shù);bp為永態(tài)轉(zhuǎn)差系數(shù);死區(qū)Ⅱ為開度死區(qū);p為機組功率;Cp為功率給定;死區(qū)Ⅲ為功率死區(qū);KP2為功率模式下比例增益;KI2為功率模式下積分增益;Kd2為功率模式下微分增益;Td2為功率模式下微分衰減時間常數(shù);ep為調(diào)差率。
開度模式傳遞函數(shù)為:
功率模式傳遞函數(shù)為:
2.2 隨動系統(tǒng)精細化模型
典型的調(diào)速器電液隨動系統(tǒng)主要由綜合放大器、電氣—機械/液壓轉(zhuǎn)換裝置、主配壓閥和主接力器等部分構(gòu)成。電液隨動系統(tǒng)包含諸多非線性因素,譬如液壓隨動系統(tǒng)中的主配壓閥死區(qū)非線性、主配壓閥輸出飽和非線性和主接力器速度限幅、主接力器輸出飽和非線性等,對系統(tǒng)動靜態(tài)特性存在較大影響。大量的仿真調(diào)試經(jīng)驗表明,采用簡化的一階線性模型進行仿真分析得出的參數(shù)與實際相差較遠。由此造成了一系列問題,比如為保證系統(tǒng)的動態(tài)穩(wěn)定性,只能大幅度調(diào)小綜合放大器的放大倍數(shù)或調(diào)大內(nèi)環(huán)反饋增益,結(jié)果使得難以保證系統(tǒng)靜態(tài)精度,且減緩了隨動系統(tǒng)的響應(yīng)速度,導(dǎo)致隨動系統(tǒng)輸出滯后于控制器輸出,惡化了動態(tài)品質(zhì)。因此,在進行調(diào)節(jié)系統(tǒng)建模時,必須將隨動系統(tǒng)一系列非線性因素加以考慮,建立精細化模型。
綜合考慮各類死區(qū)、飽和限幅和開關(guān)機時間分段調(diào)整等非線性因素,建立兩段開啟、三段關(guān)閉的隨動系統(tǒng)非線性精細化數(shù)學(xué)模型,如圖2 所示。
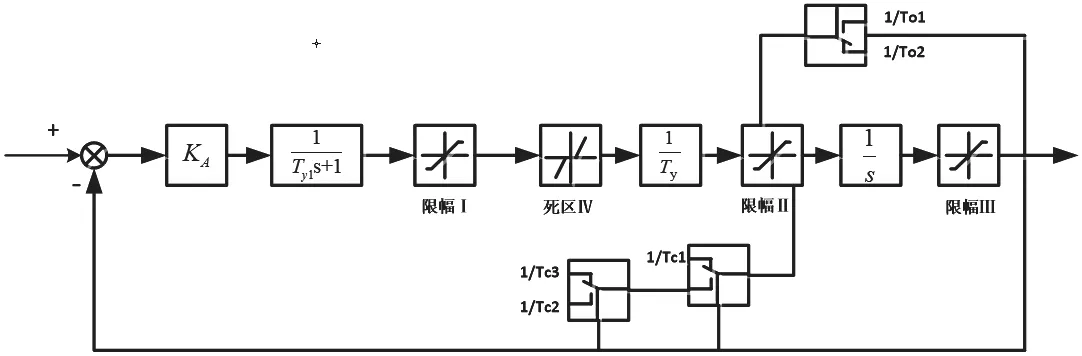
圖2 隨動系統(tǒng)二段開啟、三段關(guān)閉模型
圖2中KA為綜合放大器放大倍數(shù)為第一級液壓放大環(huán)節(jié)的傳遞函數(shù);限幅Ⅰ為主配壓閥限幅;死區(qū)Ⅳ為主配壓閥搭疊量造成的死區(qū),Ty為接力器反應(yīng)時間常數(shù);限幅Ⅱ為接力器速度對應(yīng)的限幅;限幅Ⅲ為接力器行程限幅。對于不同的開關(guān)閉特性相應(yīng)模型,分別以不同開啟速度1/To1、1/To2,不同的關(guān)閉速度1/Tc1、1/Tc2、1/Tc3等對接力器開關(guān)閉速度進行整定,實現(xiàn)兩段開啟與三段關(guān)閉。
2.3 外特性水輪機模型
水輪機外特性一般由水輪機模型綜合特性曲線與飛逸特性曲線描述,是水輪機內(nèi)部流動規(guī)律的外在表現(xiàn),可以表示水輪機在不同工況下的能量轉(zhuǎn)換特性。兩種曲線均可以通過模型試驗或現(xiàn)場試驗獲取。由水輪機單位參數(shù)公式、出力公式及力矩公式知:
由上述式(3)~(6)可推出單位力矩公式:
因此通過讀取模型綜合特性上不同單位流量、不同等開度線下的效率值則可計算得到水輪機的力矩特性,流量特性則可直接讀取得到。但模型試驗得到的模型綜合特性曲線只涵蓋水輪機運行的高效區(qū),不包括空載、開機等過渡工況區(qū)域,因此通常采用特征曲線外延的方法來補全水輪機全工域特性,以此得到完整的水輪機流量特性與力矩特性,來表征水輪機動態(tài)特性。本文基于模型綜合特性曲線與飛逸特性曲線等外特性曲線,建立外特性水輪機模型來描述水輪機流量特性與力矩特性隨轉(zhuǎn)速、導(dǎo)葉開度的動態(tài)變化關(guān)系如圖3 所示。
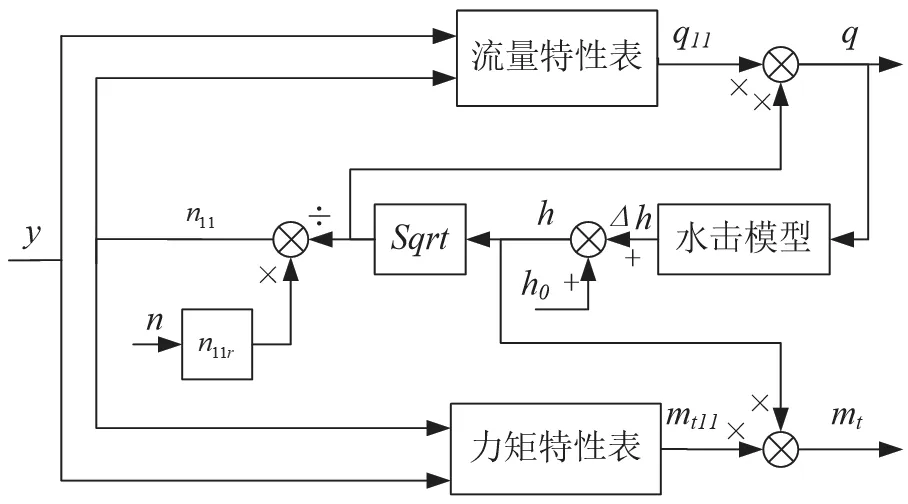
圖3 外特性水輪機模型
圖3 中y為隨動系統(tǒng)輸出的導(dǎo)葉開度;n為機組轉(zhuǎn)速;n11為單位轉(zhuǎn)速;n11r為額定單位轉(zhuǎn)速;q為機組流量;q11為單位流量;h為水頭;mt為機組輸出力矩;mt11為額定單位力矩。
在進行水輪機全工域特性補全時,主要以飛逸特性曲線為限制線,以模型綜合特性曲線獲取的流量、力矩數(shù)值為基礎(chǔ),采用恰當?shù)臄?shù)值擬合方法來補全小開度區(qū)域的數(shù)據(jù)。最終得到的水輪機流量特性與力矩特性如圖4、圖5 所示。
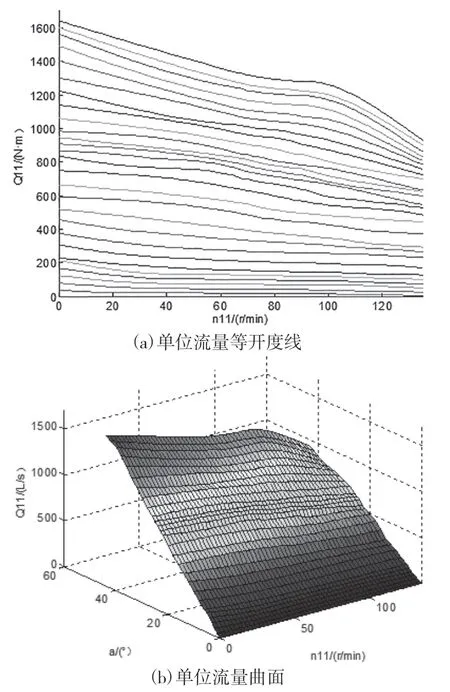
圖4 水輪機流量特性

圖5 水輪機力矩特性
2.4 引水系統(tǒng)模型
由于引水系統(tǒng)結(jié)構(gòu)多樣化和水流狀況的復(fù)雜性,引水系統(tǒng)蘊含著豐富的非線性動態(tài)特性,建立引水系統(tǒng)精確模型存在較大困難,且與水機電耦合求解時過于復(fù)雜。調(diào)節(jié)系統(tǒng)建模時大多依據(jù)引水管道的長度來選擇采用剛性或彈性水擊模型,本文引水系統(tǒng)采用彈性水擊模型進行描述,其傳遞函數(shù)為:
式中:hw=Tw/Tr,為水輪機管道特性系數(shù);TW為水流慣性時間常數(shù),s;Tr為水擊波相長,s;q和h分別為水輪機流量和水輪機工作水頭標幺值的拉氏變換;s 為拉普拉斯算子。
2.5 發(fā)電機模型
發(fā)電機作為機械能轉(zhuǎn)化為動能的核心設(shè)備,其性能同時受多種因素影響,包括發(fā)電機本身作為旋轉(zhuǎn)剛體具有的機械慣性、發(fā)電機功率與關(guān)系、勵磁系統(tǒng)以及d、q 軸繞組阻尼等。電站水輪機調(diào)節(jié)系統(tǒng)動態(tài)性能僅受發(fā)電機轉(zhuǎn)速變化過程影響,將發(fā)電機作為旋轉(zhuǎn)剛體考慮即可滿足仿真計算精度要求,采用一階模型描述,傳遞函數(shù)為:
式中:Ta為機組慣性時間常數(shù);en=eg-ex,其中ex為水輪機力矩對轉(zhuǎn)速的偏導(dǎo)數(shù),eg為發(fā)電機力矩對轉(zhuǎn)速的偏導(dǎo)數(shù);en計算時只考慮負載與電網(wǎng)的影響,水輪機的ex已反映在水輪機模型中;s為拉氏算子。
3 機組動態(tài)特性仿真
以某大型水利樞紐電站為例,基于上述建立的調(diào)節(jié)系統(tǒng)非線性模型,進行機組甩負荷、一次調(diào)頻等動態(tài)特性仿真。根據(jù)提供的資料,電站水輪機采用混流式水輪機,機組的相關(guān)參數(shù)如表1 所示。

表1 機組參數(shù)表
3.1 機組甩負荷動態(tài)過程仿真
水輪機甩負荷作為水輪發(fā)電機組在日常運行中常見的大波動過渡過程,機組甩負荷過程中會造成最大轉(zhuǎn)速上升值和最大壓力上升值等參數(shù)的急劇變化,若設(shè)計不當,將引發(fā)安全事故,嚴重威脅電站安全穩(wěn)定運行,因此對于機組甩負荷工況加以研究對電站安全運行具有重要指導(dǎo)意義。根據(jù)電站提供的實測甩負荷數(shù)據(jù),分別驗證甩小負荷175 MW(25%Pr)和大負荷756 MW(108%Pr)。設(shè)定負荷相應(yīng)的接力器行程與導(dǎo)葉開度百分數(shù),調(diào)整仿真初始工況出力穩(wěn)定后,設(shè)定適當?shù)姆抡鏁r長,進行甩負荷。待仿真結(jié)束,讀取仿真計算結(jié)果,將得到的仿真結(jié)果繪制曲線與實測曲線對比,如圖6、圖7所示。
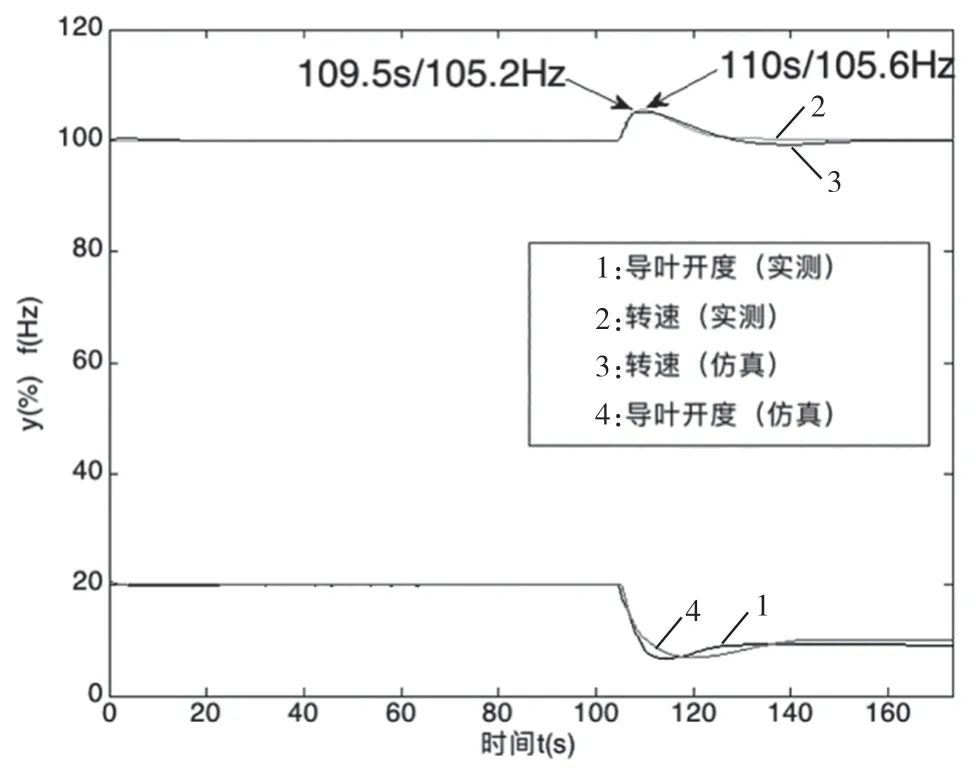
圖6 機組甩175 MW 負荷
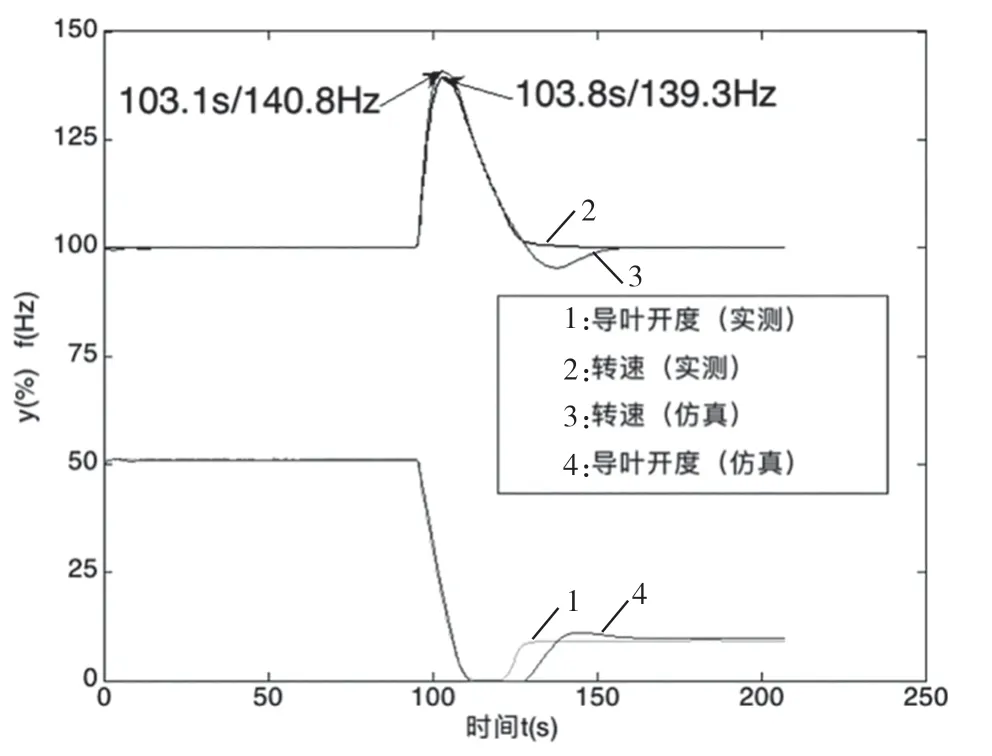
圖7 機組甩756 MW 負荷
由圖6、圖7 中轉(zhuǎn)速變化曲線對比知:仿真轉(zhuǎn)速上升速度略快于實測轉(zhuǎn)速上升,達到轉(zhuǎn)速上升峰值的時間早,仿真峰值105.2 s/139.3 Hz 略小于實測峰值106.6 s/140.8 Hz,峰值誤差最大不超過1.1%,仿真轉(zhuǎn)速與實測轉(zhuǎn)速下降過程趨勢基本一致,吻合得較好。
由圖6、圖7 中導(dǎo)葉開度變化曲線對比可知:當機組甩756 MW 負荷時,兩者導(dǎo)葉關(guān)閉規(guī)律吻合較好;當機組甩175 MW 負荷時,導(dǎo)葉開度變化吻合性較差。誤差產(chǎn)生的原因可能是缺乏小開度的飛逸特性曲線,采用大開度外延的小開度飛逸與實際情況有一定的偏差,插補的制動區(qū)力矩特性與實際值存在差異導(dǎo)致轉(zhuǎn)速峰值與轉(zhuǎn)速下降速度存在差異。
通過上述機組甩大、小負荷過程分析可知,所建立的模型能夠較為準確反映機組甩負荷過渡過程中的動態(tài)特性。
3.2 一次調(diào)頻動態(tài)過程仿真
根據(jù)電站提供的真機一次調(diào)頻試驗數(shù)據(jù),分別進行開度模式和功率模式下的一次調(diào)頻仿真驗證。理論上,在開度模式下,主要考慮開度變化曲線的吻合度;在功率模式下,主要考慮功率變化曲線的吻合度。依據(jù)仿真計算結(jié)果繪制導(dǎo)葉開度變化曲線與功率響應(yīng)過程曲線對比圖,具體分析如下所述。
3.2.1 開度模式下一次調(diào)頻仿真
(1)一次調(diào)頻過程1
仿真條件為:H=102.6 m,P=603.3 MW,接力器行程百分數(shù)為47.50%,調(diào)速器參數(shù)kp=3.5、ki=0.95、kd=0,永態(tài)轉(zhuǎn)差系數(shù)Bp=0.04,頻率擾動Δf=+0.15 Hz,開度和功率響應(yīng)過程對比如圖8 所示。
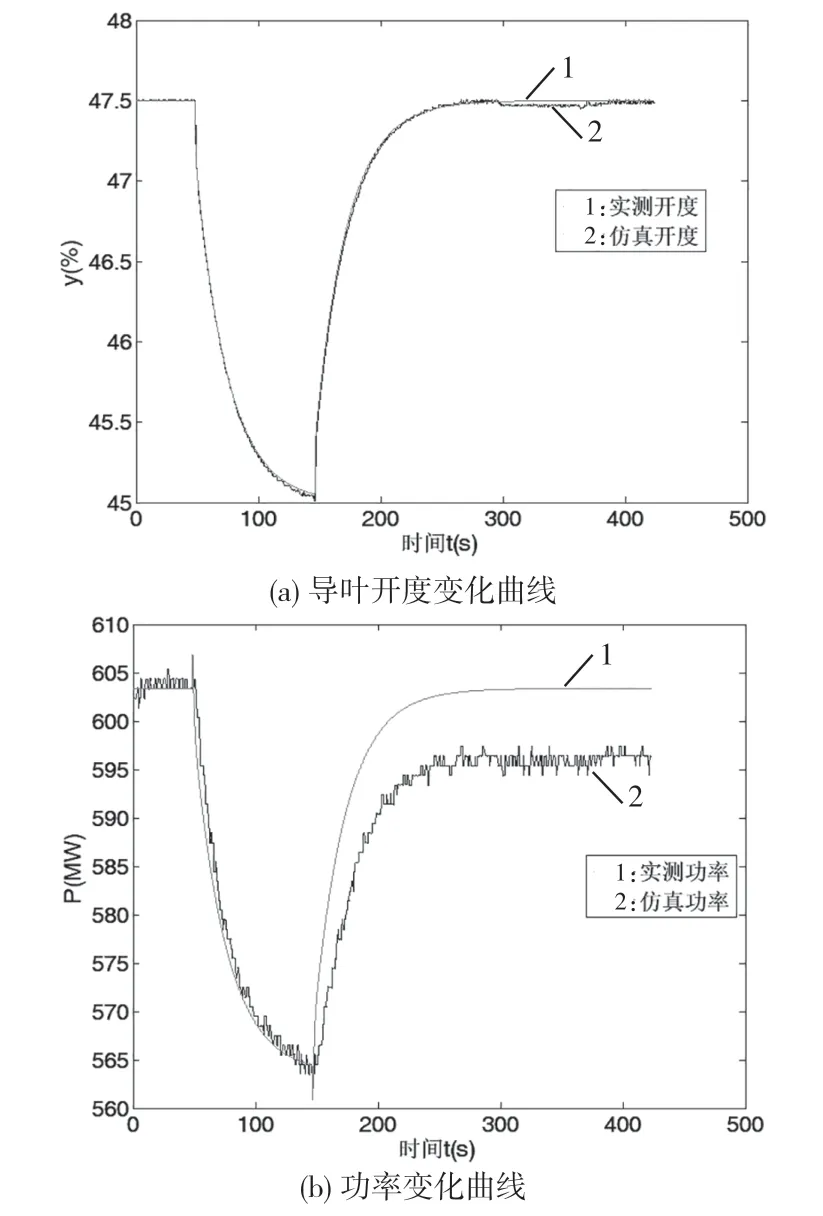
圖8 開度模式一次調(diào)頻過程1
(2)一次調(diào)頻過程2
仿真條件為:H=102.5 m,P=602.3 MW,接力器行程百分數(shù)為47.50%,調(diào)速器參數(shù)kp=6、ki=10、kd=0,永態(tài)轉(zhuǎn)差系數(shù)Bp=0.04,頻率擾動Δf=±0.16 Hz,開度和功率響應(yīng)過程對比如圖9 所示。
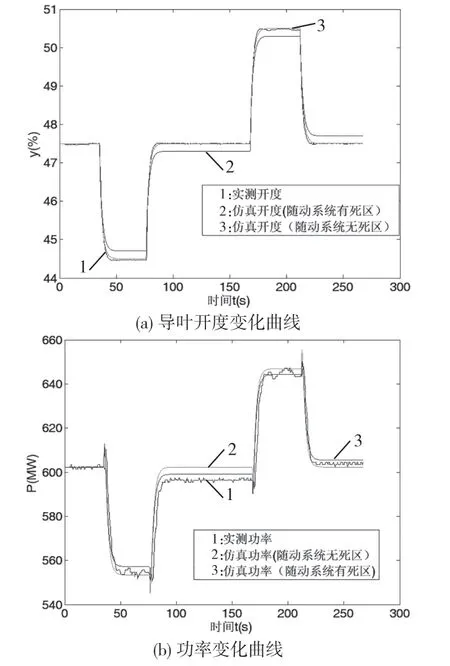
圖9 開度模式一次調(diào)頻過程2
由圖8、圖9 知,一次調(diào)頻動態(tài)響應(yīng)過程中,仿真導(dǎo)葉開度變化與實測導(dǎo)葉開度變化過程與趨勢基本一致,吻合得較好;仿真功率開始調(diào)節(jié)時間略微早于實測,這是由于機組實際調(diào)節(jié)過程中,功率變送器具有較大常數(shù),故實測功率滯后;在導(dǎo)葉開度增大回到初值后,仿真功率大于實測功率,兩者存在一定偏差。仿真過程中,隨動系統(tǒng)增加死區(qū)后,擾動消失后仿真導(dǎo)葉開度略小于初值,因此仿真功率也略低于初始功率,因而仿真功率與實際功率存在偏差應(yīng)該是受隨動系統(tǒng)死區(qū)影響所致。
通過上述兩種不同頻差、不同PID 參數(shù)下的一次調(diào)頻響應(yīng)的仿真與實測對比分析可知,所建立的模型能夠高度準確反映開度模式下機組一次調(diào)頻過程中的開度變化過程,能應(yīng)用于機組一次調(diào)頻動態(tài)性能研究。
3.2.2 功率模式下一次調(diào)頻仿真
仿真條件為:H=102.3 m,P=619 MW,接力器行程百分數(shù)為48.75%,調(diào)速器參數(shù)kp=7、ki=1.4、kd=0,調(diào)差率Ep=0.04,頻率擾動Δf=±0.18 Hz,在兩種不同擾動下,開度和功率響應(yīng)過程對比分別如圖10、圖11 所示。
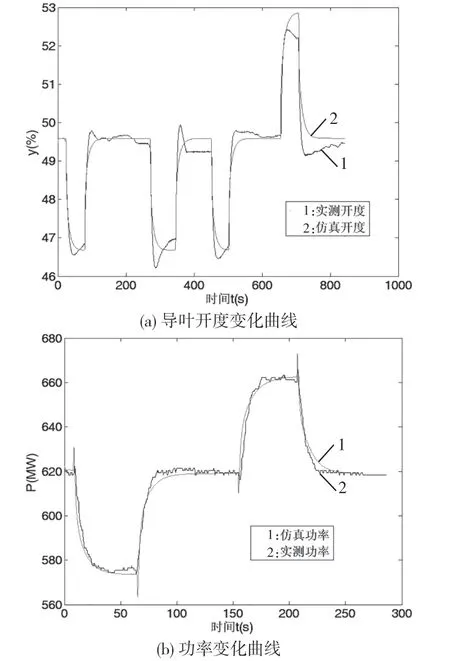
圖10 功率模式一次調(diào)頻過程1
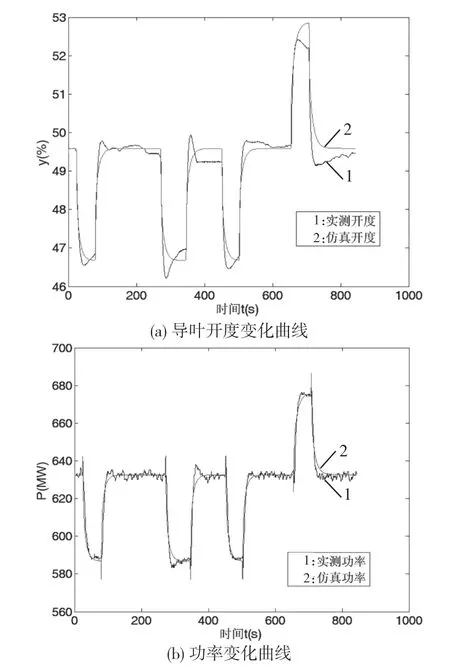
圖11 功率模式一次調(diào)頻過程2
功率調(diào)節(jié)模式下,維持實際功率與目標功率一致。由圖10(b)、圖11(b)知,在多次連續(xù)頻率擾動作用下,仿真功率開始調(diào)節(jié)時間略微早于實測,因為實際中功率變送器具有較大常數(shù),故實測功率滯后;仿真與實測功率總體變化趨勢基本一致,實測功率在調(diào)節(jié)過程呈微小波動狀態(tài),仿真功率曲線較為光滑。
從圖10(a)、圖11(a)可看出,仿真與實測開度變化存在差異。在頻率上升與恢復(fù)過程中,仿真與實測功率變化基本一致,頻差消失后,實際導(dǎo)葉開度值略大于仿真開度值。在頻率下降與恢復(fù)過程中,仿真與實測功率變化基本一致,仿真開度最終值略大于實測開度,這可能是水頭變化或測量誤差所致。
通過上述兩種不同頻率擾動下的一次調(diào)頻對比分析可知,所建立的模型能夠高度準確反映功率模式下機組一次調(diào)頻過程中的功率響應(yīng)過程,能應(yīng)用于機組一次調(diào)頻動態(tài)性能研究。
4 結(jié)論
本文重點針對調(diào)速器隨動系統(tǒng),綜合考慮其各類死區(qū)、飽和限幅和開關(guān)機時間分段調(diào)整等非線性因素,建立了隨動系統(tǒng)非線性精細化模型;針對水輪機,建立外特性水輪機模型,最終建立了能夠準確反映水電機組甩負荷大波動過渡過程及一次調(diào)頻動態(tài)響應(yīng)過程的水輪機調(diào)節(jié)系統(tǒng)非線性模型。通過真機試驗數(shù)據(jù)與仿真數(shù)據(jù)對比,驗證了本文建立的包含非線性因素的模型的優(yōu)越性和準確性。

