牛頓環測量數據的不確定誤差參數統計分析*
張 森 張 江 曹南斌
(河北地質大學數理教學部 河北 石家莊 050031)
1 引言
在大學物理實驗中,最普遍的等厚干涉實驗是牛頓環實驗.最早的牛頓環實驗是1675年牛頓在制作天文望遠鏡時,偶然發現將一個望遠鏡的物鏡放在平板玻璃上,就可以實現光學中常見的定域等厚干涉現象.牛頓環在大學物理實驗數據誤差處理教學中起著重要作用,更精確的牛頓環估計方法將提高學生對等厚干涉和誤差統計分析領域的理解[1-2].
牛頓環實驗基本方法是通過讀數顯微鏡對牛頓環的干涉條紋進行測量,進而計算出平凸鏡的曲率半徑.為了提高曲率半徑的測量精度,人們從各方面進行了詳細研究.計算機軟件在誤差統計分析數值處理中起到了決定性作用[3].在壓力的作用下,平凸鏡在接觸面附近發生了不可避免的彈性形變,使得暗斑“吞噬”了若干條明暗圓環,因此,實驗只能精確測出暗環的直徑,卻很難確定暗紋的誤差不確定度.所以,既然誤差不可避免,我們將注意力轉移到如何構建更準確的統計模型,并進一步得到測量數據的最佳估計值,從而提高計算曲率半徑的精度.同時,建立牛頓環測量數據不確定誤差參數統計模型對于牛頓環在測量薄膜、玻璃彈性模量、液體折射率等方面應用也具有重要意義.
在過去幾十年,高等院校大學物理實驗主要使用兩種不同的實驗方法分析牛頓環實驗數據:逐差法和最小二乘法.逐差法一般采用的方法是把測量的偶數個數據對半分成前后兩組,后一組的數據與前一組的對應數據逐差再取平均.最小二乘法是統計學中最常見的回歸分析方法.最近十幾年,眾多物理實驗對測量不確定度分析要求越來越高,這對大學物理實驗教學研究起到了極大促進作用.然而,不同方法測定的牛頓環平凸透鏡的曲率半徑有一定的差異,這是多年以來存在于實驗教學領域尚需討論的疑難問題[4-5].如果實驗數據存在特殊的離群點,那就需要選擇更穩健的誤差統計分析方法.
不同大學物理實驗方法測量結果之間的偏差是長期困擾廣大師生的難題.為此不同學派的理論學家提出了多種不確定度統計模型解釋.對于穩健性統計模型,我們已經基于實驗數據集,將MFV統計方法(most frequent value),應用到觀測數據最佳估計值問題[6-7].在我們之前的工作顯示,誤差分布完全可能是非高斯的,且測量數據之間可能存在無法精確衡量的相關性.
加權平均方法也是一種常見誤差處理統計方法.應用加權平均方法要滿足一些假設,包括數據在統計意義下獨立分布和隨機誤差滿足高斯分布.然而實驗測量的誤差分布可能是非高斯的,采用加權平均方法不一定能夠得到合理的中心估計和不確定度置信區間.中位數方法具有對異常值不敏感特性,已經有很多應用中位數統計處理實驗數據集的工作[8].
在非高斯分布情況下,傳統方法的應用受到了巨大限制.為詳細分析測量過程中的統計誤差和系統誤差,許多研究人員選取誤差參數模型分析物理測量數據.文獻[9]在2020年應用貝葉斯分層模型,計算出實驗數據的擬合值.文獻[10]應用頻率學派方法構造了一種具有優良穩健性的模型,該模型對數據誤差的建模分析較為全面.
本文將詳細分析Cowan的統計方法,以及頻率學派不確定誤差參數統計模型的構造和計算過程.基于河北地質大學物理實驗協會學生測量的牛頓環6~15級實驗數據結果,如表1所示,重新構建其不確定誤差參數統計模型,以減小異常值的影響.最后給出數值計算擬合結果.
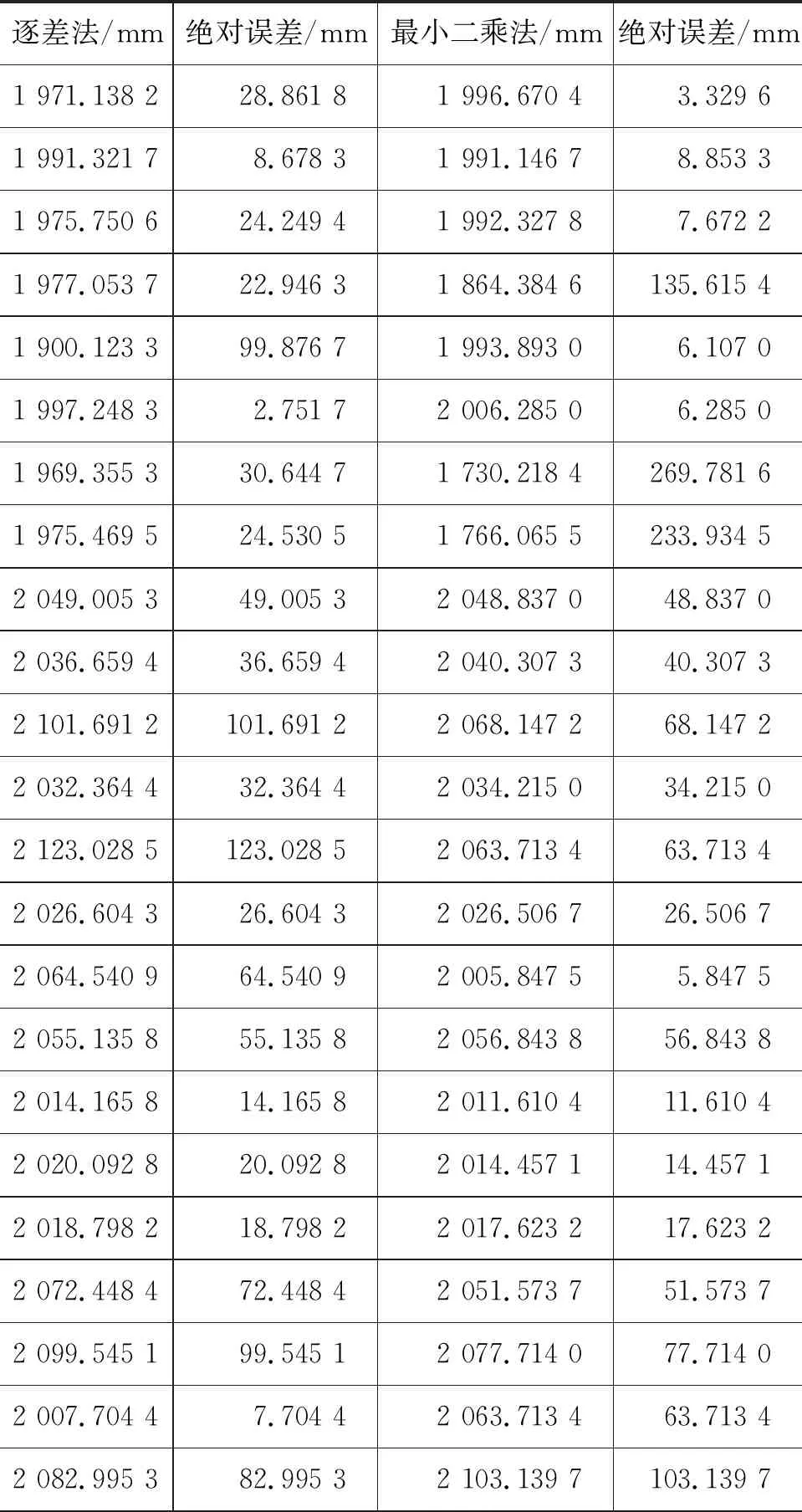
表1 牛頓環實驗曲率半徑數據結果
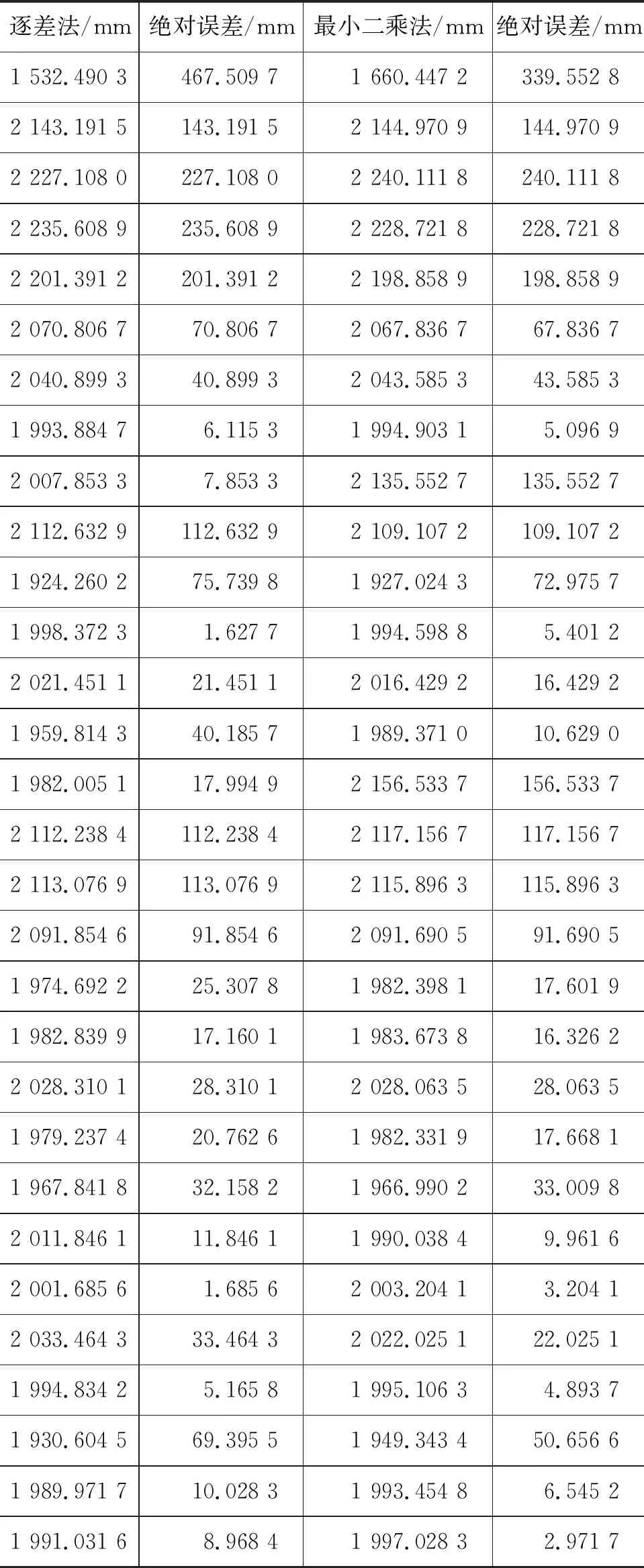
續表1
2 頻率學派統計方法
2.1 參數估計和置信區間
頻率學派參數估計常用方法為極大似然估計和最小二乘法.這兩種方法的應用均需滿足一定的假設,特別是在應用極大似然估計時,需要預先假設數據的分布.通過引入額外的冗余參數,可以降低可能出現的錯誤先驗信息影響,從而提升模型的穩健性,但這可能會使得模型的計算更為復雜.
基于頻率學派對概率的定義,頻率學派置信區間邊界由測量數據的函數給出.其定義為:覆蓋概率指一個集合中包含參數真實值的概率.構造置信區間使覆蓋概率大于給定的置信度.觀測值Y的概率密度函數為p(y|θ),其中θ是未知參數.對參數θ和置信度1-α,有y1(θ,α)與y2(θ,α),滿足
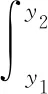
(1)
通常y1(θ,α)與y2(θ,α)是單射,因此在給定的置信度下,可以求出反函數θ1(y)和θ2(y).假設y0與θ0分別為物理量真值和參數真值.則θ0落在[θ1,θ2]當且僅當y0落在[y1(θ0),y2(θ0)],對于所有的θ0值均成立.因此
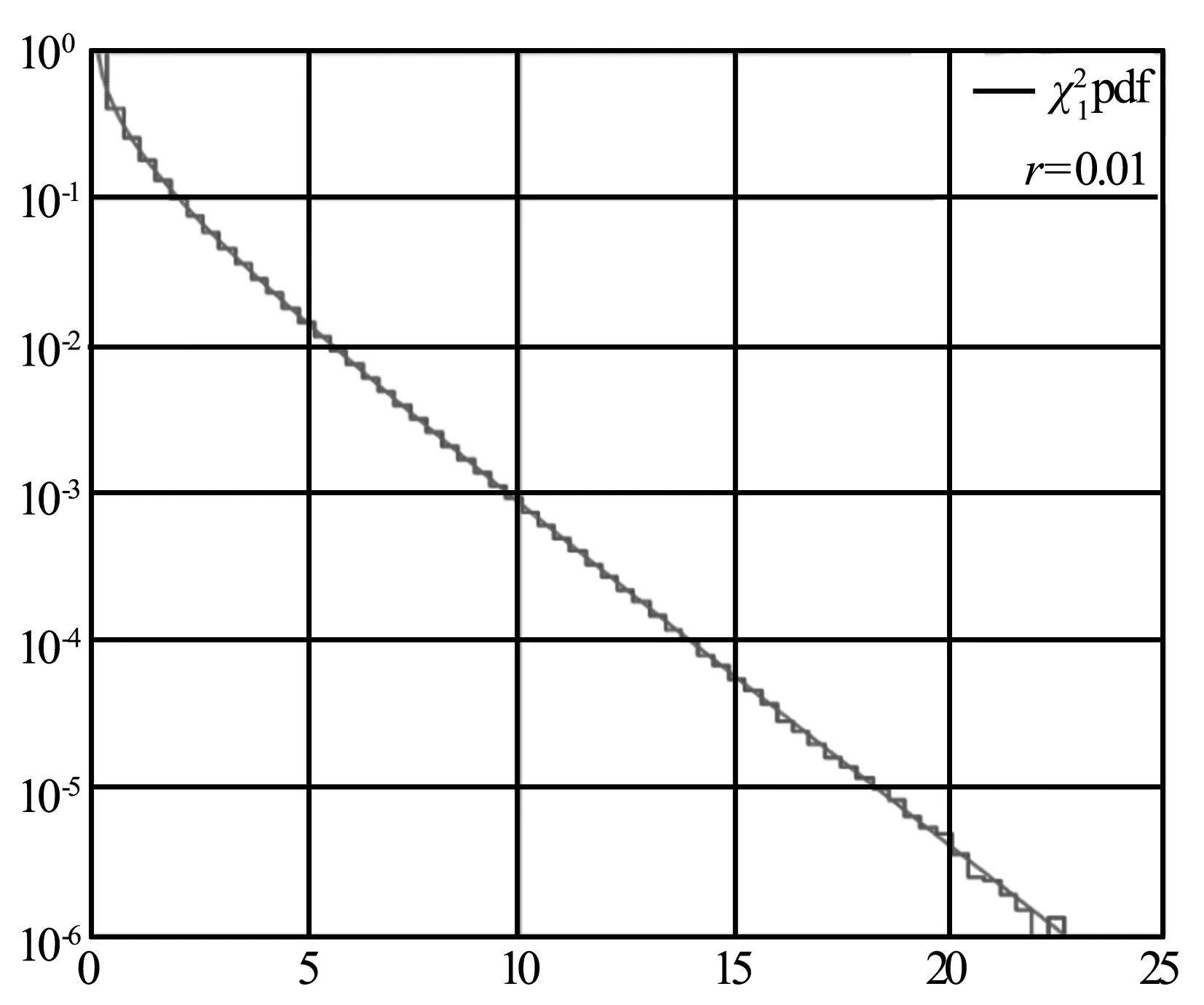
1-α=P[y1(θ) (2) 這就是置信區間的Neyman構造方法.置信區間構造方法并不唯一,常見選取置信區間方法為:選取中心對稱區間、單側區間,或構造似然比統計量進行檢驗求解.另外,若觀測值服從離散分布,置信區間的覆蓋概率可能大于1-α. 頻率學派置信區間的構造方法與假設參數真值為θ0,并對其進行假設檢驗是等價的.常用的一種檢驗為似然比統計量檢驗,似然比λ定義為 (3) (4) 置信區間的數值計算有時會很困難,可以通過蒙特卡羅(MC)方法求解.如果模型中使用似然函數較為復雜,那么運算過程中將包含較多難算的最優化問題. 對于構造似然比時引入冗余參數,Cowan提出一種應用輪廓似然比(profile likelihood ratio)統計量的不確定誤差參數統計模型.此模型對數據誤差應用Gamma分布進行建模,通過調整超參數r,得到具有優良穩健性的擬合結果.輪廓似然比定義為 (5) 圖1展示了正態分布樣本的輪廓似然直方圖與χ2分布的對比.紅色直線代表標準的χ2分布PDF,樣本輪廓似然比的MC模擬結果在歸一化后顯示為藍色直方圖.在滿足一定假設的前提下,-2lnλ服從χ2分布.然而若某些假設條件不成立,比如參數間有著相關性的條件下,-2lnλ則并不總是服從χ2分布. 圖1 特定參數下-2ln λ的分布 對于牛頓環實驗數據統計分析問題,可以選取高斯分布的似然函數,而對誤差應用Gamma分布模型進行刻畫.通過超參數控制誤差波動,可以在實驗數據集上得到較好的擬合效果.高斯分布通常被認為是在許多未知影響因素相互疊加時的近似分布,這里為p(y|μ,θ)選取高斯分布的似然函數是合理的.可以構造如下似然函數 (6) 這代表假設觀測數據y服從一個高斯分布,其參數為μ,θ.θ的估計值為u,假設其服從高斯分布,即 (7) (8) (9) (10) (11) 調整超參數r的值,可以控制模型對于異常值的敏感性. 在對模型參數進行化簡后,對數似然函數為 (12) 圖2 模型在一組實驗數據上的擬合結果 計算所得的牛頓環測量數據估計值及其置信區間如圖3所示.圖中曲線代表負對數似然作為參數μ的函數,根據Wilks定理,使得-2lnλ從最小值增大1時的μ值即為其68.3%置信區間的邊界,在圖中以豎直虛線顯示.不同的子圖顯示了不同參數設置下的擬合結果.計算得到,選取r=0.2時,牛頓環測量數據估計值為R=1 998.79,對應的置信區間邊界為[1 990.34,2 007.32].當r=0.4時的置信區間總長略大于r=0.2時的結果,這與之前的模型分析吻合. 圖3 模型計算結果 此外,模型對采用逐差法的數據擬合結果為R=1 998.25-9.71/+9.47,對最小二乘法的數據結果為R=1 998.97-7.47/+7.90.在計算過程中,當r=0.6時,-2lnλ的函數曲線有更多的起伏,這表示當r過大,模型的預測效果可信度較低.因此,我們選取參數值r=0.2作為最優參數值. 圖4對比了牛頓環實驗測量數據和不同統計模型計算結果,圖中陰影部分為不確定誤差參數模型計算所得的置信區間.在垂直虛線左側為隨牛頓環實驗變化的測量數據列,右側為模型擬合結果,包括加權均值、中位數以及本文得到的結果.圖4下方子圖展示了以誤差統計模型為基準進行歸一化之后的結果. 此誤差統計模型的重要特性之一是,隨著參數值的增加,擬合數據的值對顯著偏離中心值的游離點(異常值)變得不那么敏感.圖4中體現出了這種特性,結合在實驗數據上的擬合效果,最終我們選取參數值r=0.2.此時的不確定誤差參數統計模型相比起中位數結果更接近于數據整體的加權均值,且對數據有著較好的覆蓋率. 圖4 原始數據分布及模型預測結果對比(下方子圖為歸一化后的相對誤差分布) 總而言之,物理實驗的一個主要目標是對一些關鍵物理量進行精確測量.牛頓環實驗數據不同方法間長期存在的偏差是基礎光學和大學物理實驗數據處理的疑難問題之一.對牛頓環測量誤差進行穩健統計建模分析是獲取可信估計值及置信區間的關鍵.本文應用Cowan不確定誤差參數統計模型,對牛頓環實驗數據使用Gamma分布對誤差建模,得到曲率半徑估計值為R=1 998.79-8.45/+8.53,計算結果顯示出良好的穩健性,并且對異常值的干擾不敏感. George E. P. Box 指出:“所有模型都是錯誤的,但有些模型是有用的”.每個計算統計模型的一些潛在假設并不一定都嚴格成立.Gamma誤差模型在一定程度上可以克服傳統方法不實假設的問題,這也啟發我們在類似情況下應用不確定誤差參數模型,并進一步研究其他大學物理實驗測量數據的不確定度問題.2.2 似然比統計量的構造和應用
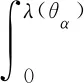
2.3 不確定誤差參數統計模型
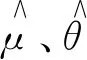
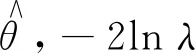
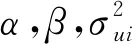

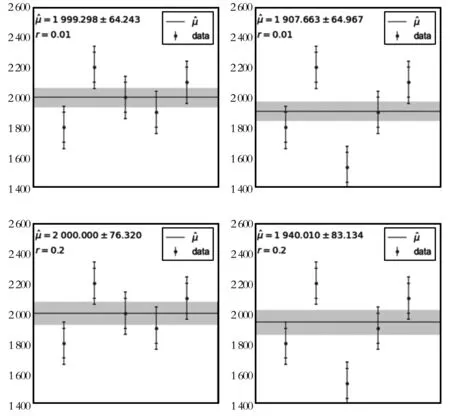
3 模型計算結果
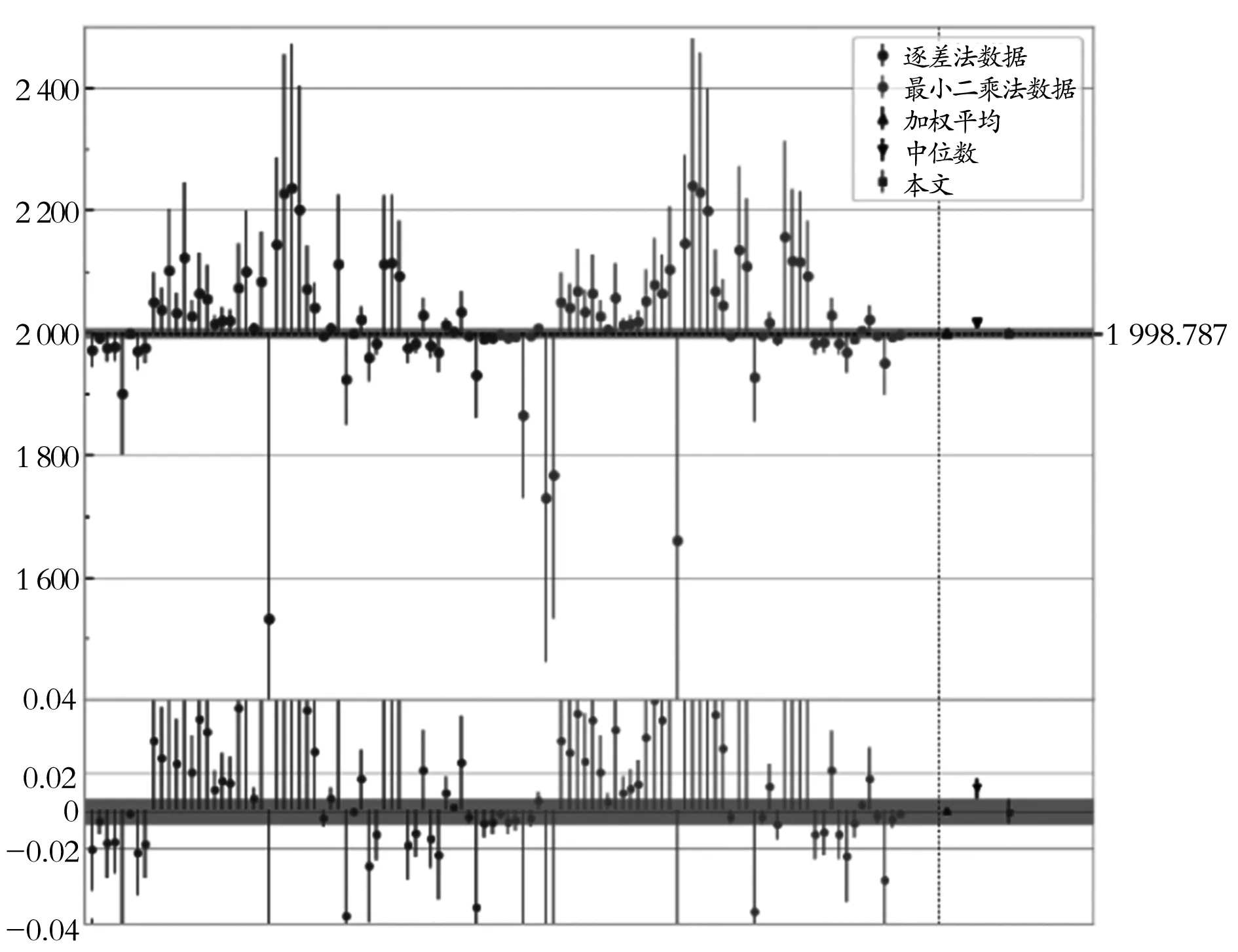
4 結論

