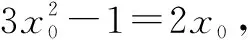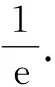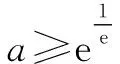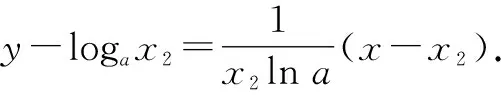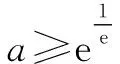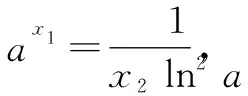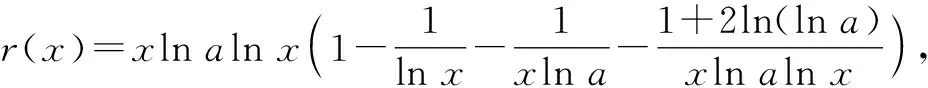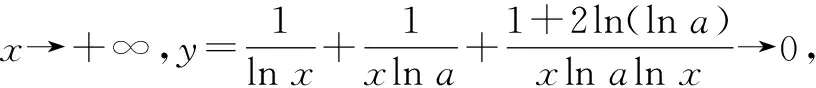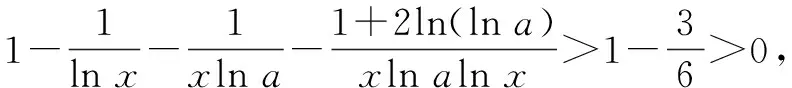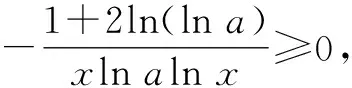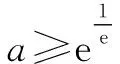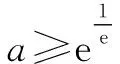基于思維導圖的高考試題解法研究
——2022全國甲卷文科數學第20題的探究
代錦春
?云南師范大學附屬世紀金源學校
代紅軍
?昆明市官渡區第六中學
朱俊霖
?西南大學數學與統計學院
1 題目呈現
(2022全國甲卷文科數學第20題)已知函數f(x)=x3-x,g(x)=x2+a,曲線y=f(x)在點(x1,f(x1))處的切線也是曲線y=g(x)的切線.
(1)若x1=-1,求a;
(2)求a的取值范圍.
2 解析
本題第(1)(2)問分析及解答過程如下.
對于第(1)問,已知函數f(x)與函數g(x)的公切線與f(x)切點的橫坐標為x1=-1,可以從以下三個角度求參數a的值. 角度一,寫出f(x)在x1=-1處的切線,可以選擇聯立切線方程與y=g(x),借助Δ=0求a;也可以借助兩函數在兩切點處的導函數值相等,建立x1=-1與x2的關系式,再由切點(x2,y2)同在切線與函數g(x)上,建立a的方程求a.角度二,設出g(x)在點(x2,y2)處的切線,先探究x1=-1與x2的關系,再由切點(-1,0)在切線上,建立關于a的方程求a.角度三,分別用f(x)與g(x)的切點表示公切線,根據兩切線斜率相等、截距相等構建關于x2與a的二元方程組,從而解出a的值.相應的思維導圖如圖1所示.
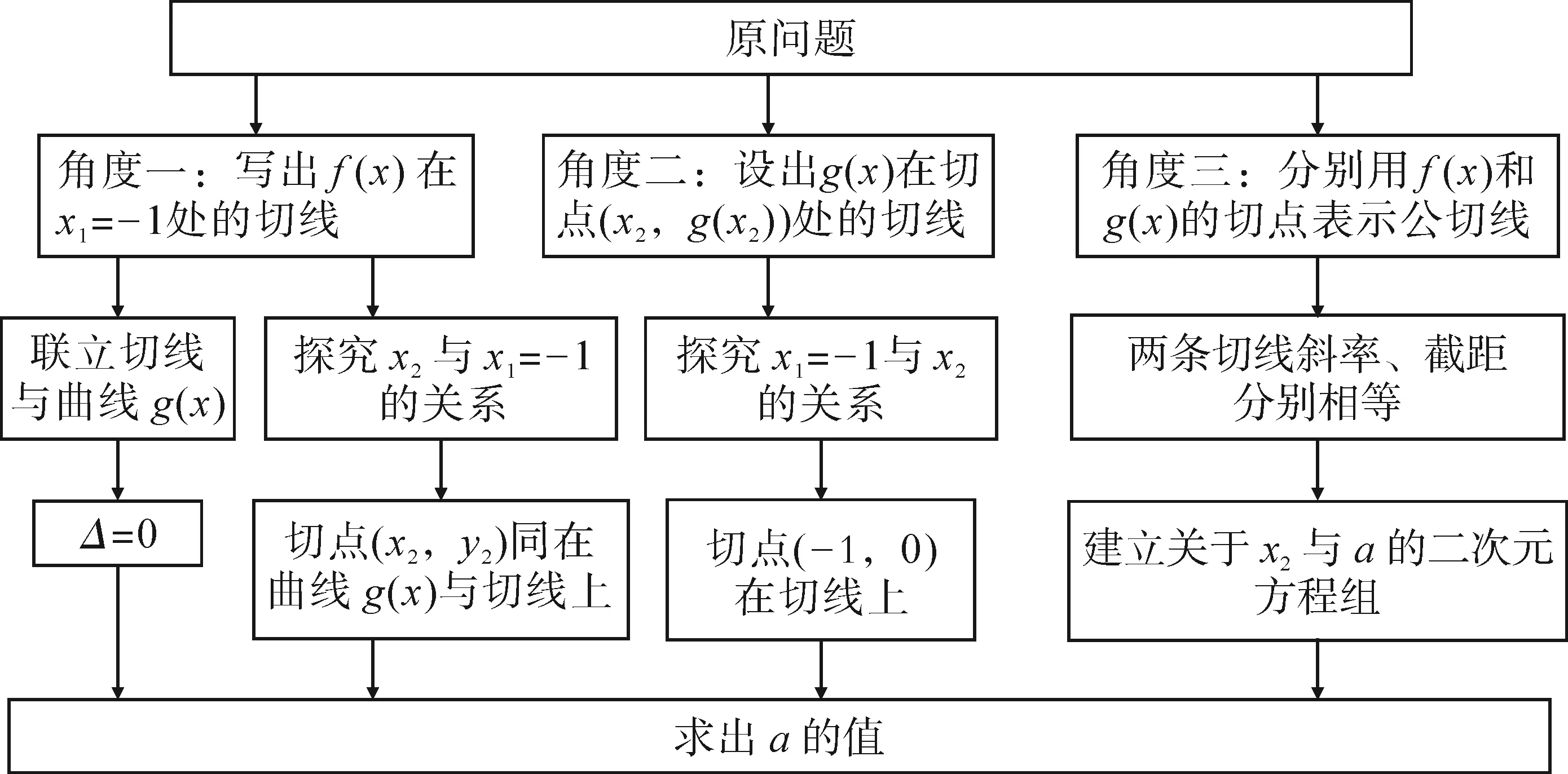
圖1
角度一:寫出f(x)在x1=-1處的切線.
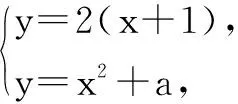
解法2-1:由f′(-1)=2,可知f(x)在x1=-1處切線l的方程為y=2(x+1).
因為切線l與曲線y=g(x)相切于點(x2,y2),所以g′(x2)=f′(-1),即2x2=2,得x2=1.
由于點(x2,y2)同在切線l與曲線y=g(x)上,故將點(x2,y2)代入l的方程,得y2=2(x2+1)=4.
因此g(x)與l相切于點(1,4),代入y=g(x),得4=12+a,解得a=3.
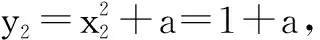
角度二:設出g(x)在切點(x2,y2)處的切線.
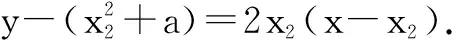
由切線l與曲線y=f(x)相切于點(-1,0),得f′(-1)=g′(x2),即2=2x2,則x2=1,從而l:y-(1+a)=2(x-1).再由點(-1,0)在切線l上,將點(-1,0)代入直線l,解得a=3.
角度三:分別用f(x)和g(x)的切點表示公切線.
解法4:f(x)在x1=-1處的切線l方程為
y=2(x+1). ①
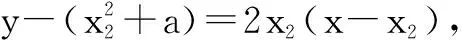
點評:解法1中利用Δ=0來構建關于a的方程求a,僅適用于g(x)為二次函數,具有一定的特殊性.在處理公切線問題時,常常借助兩函數在各自切點處的導函數值即為公切線的斜率,從而得到兩切點橫坐標的關系;再由切點同在切線與函數圖象上,建立方程組進行求解.
對于第(2)問,在此問中,f(x)的切點由定點變為了動點,類比第(1)問的探究方法,可以從以下三個角度去求參數a的范圍.角度一,用f(x)的切點表示公切線,將切線與y=g(x)聯立,借助Δ=0得出a與x1的關系,進而去求a的范圍;還可以先探究兩切點橫坐標之間的關系,由g(x)的切點同在切線與y=g(x)上,構建關于a與x1的等式,進而求a的范圍.角度二,用g(x)的切點表示公切線方程,先探究兩切點橫坐標之間的關系,由f(x)的切點同在切線與y=f(x)上,構建關于a與x1的等式,進而求a的范圍.角度三,用f(x)與g(x)各自的切點坐標表示公切線,借助公切線的兩種表達形式的斜率、截距相等得出關于a與x1的等式,進而求a的范圍.相應的思維導圖如圖2所示.
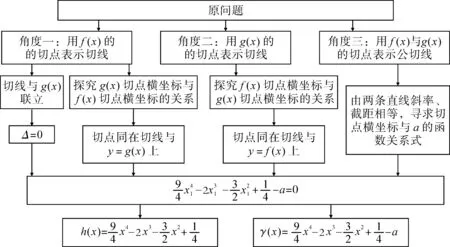
圖2
角度一:用f(x)的切點表示切線.
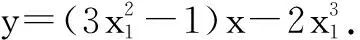
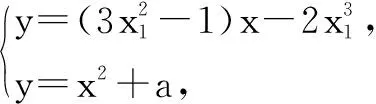
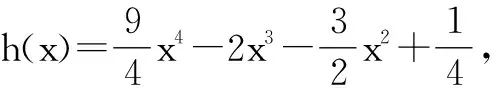
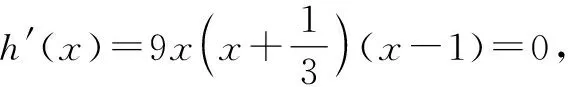
當x變化時,h′(x),h(x)的變化情況如表1所示.
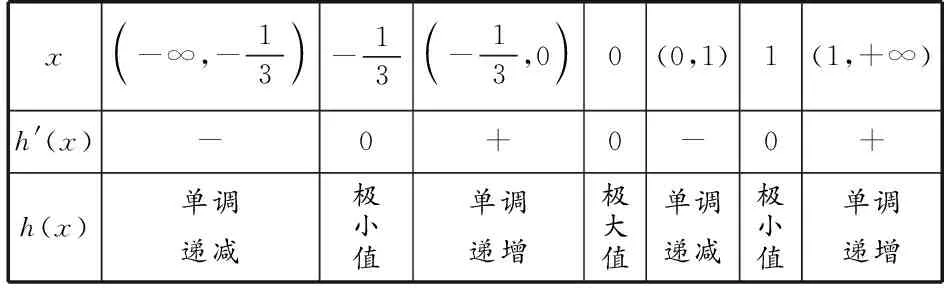
表1
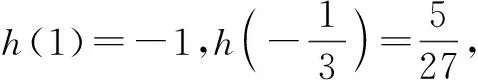
所以a∈[-1,+∞).

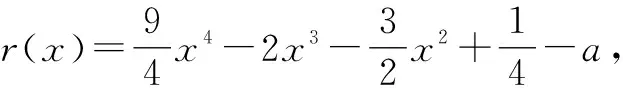
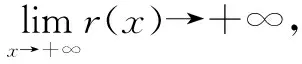
要使r(x)存在零點,即曲線y=γ(x)與x軸有交點,則r(x)min≤0,即-1-a≤0,所以a∈[-1,+∞).
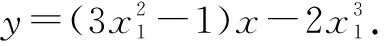
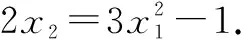
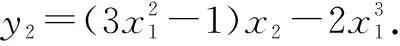
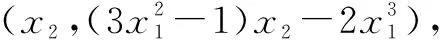
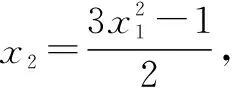
下同解法1-1或解法1-2.
角度二:用g(x)的切點表示公切線方程.
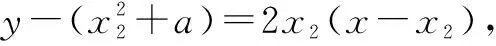
下同解法1-1或解法1-2.
角度三:用f(x)與g(x)的切點表示公切線.
解法4:曲線y=f(x)在點(x1,f(x1))處的切線l的方程為
設直線l與曲線y=g(x)相切于(x2,g(x2)),切線l的方程為
以下同解法1-1或解法1-2.
點評:從第(1)問中函數f(x)切點確定求參數a的值,到第(2)問中函數f(x)切點變化求參數a的范圍,是從特殊到一般的過程,滲透了邏輯推理的核心素養,由參數求值問題過渡到參數求范圍問題滲透了函數與方程的數學思想.本題第(1)問中處理兩曲線公切線問題的思考角度在第(2)問中仍然適用.此外,在處理求參數范圍的問題時,需先構建含有參數的等式,再轉化為兩曲線存在交點或函數存在零點的問題去求參數范圍.
3 變型題
已知函數f(x)=x3-x,g(x)=x2+a,曲線y=f(x)在點(x1,f(x1))處的切線也是曲線y=g(x)的切線,則a的取值范圍為.
秒殺法:圖象法.
函數f(x)=x3-x的圖象固定,函數g(x)=x2+a的圖象隨a的變化而沿著y軸方向變化,曲線y=g(x)與曲線y=f(x)的幾類位置關系如圖3~7.
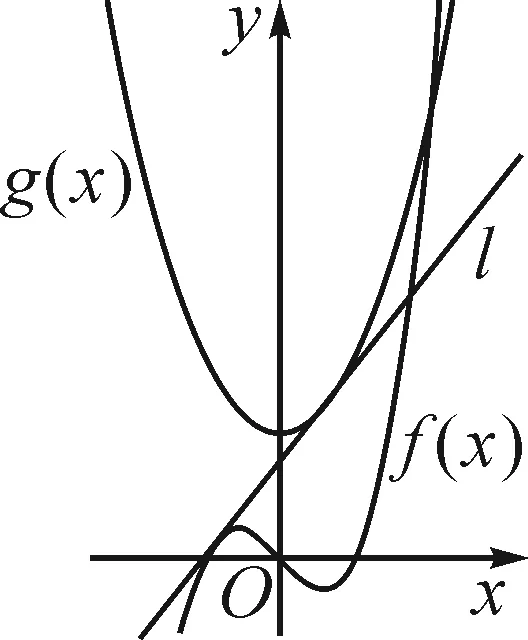
圖3
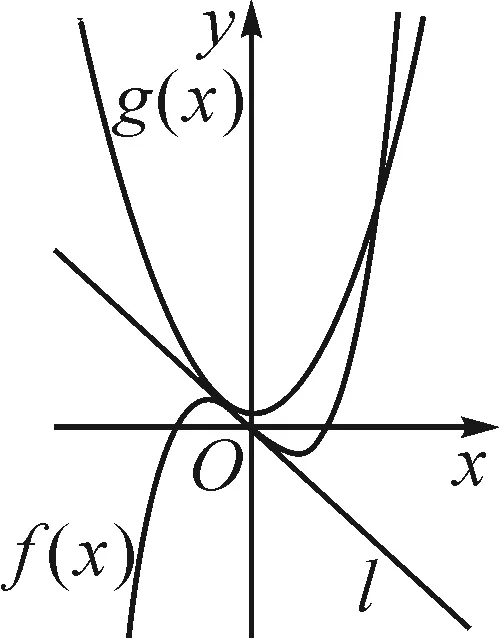
圖4
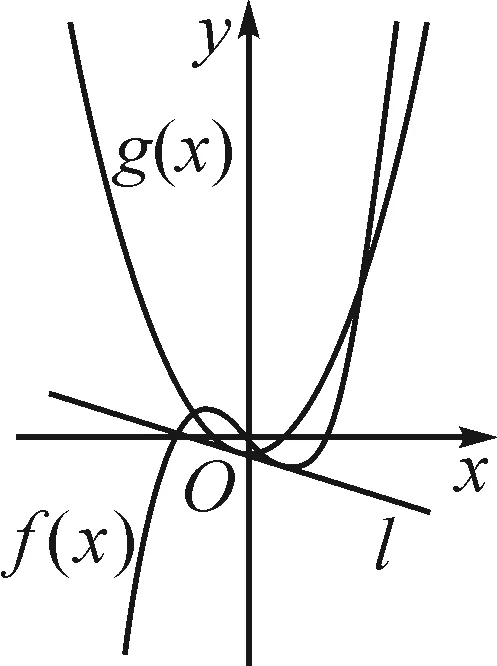
圖5
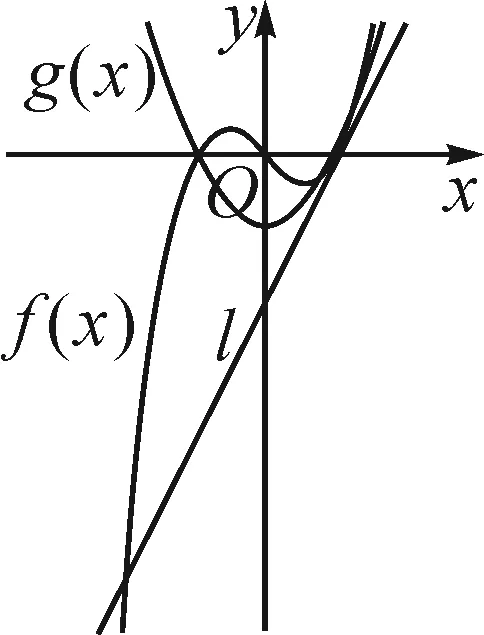
圖6
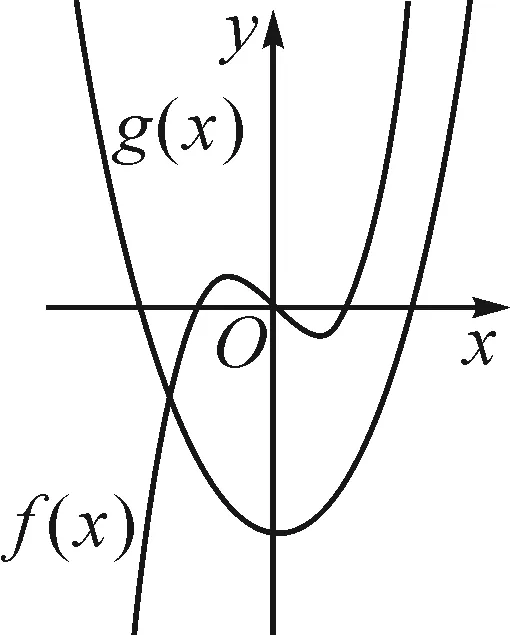
圖7
直觀觀察兩函數圖象公切線的存在情況,可以發現,當f(x)與g(x)的相對位置屬于前四種情況(圖3~6)時,兩函數圖象均能找到公切線.當f(x)與g(x)的相對位置屬于圖7所表示的情況時,在兩函數圖象交點左側,f(x)的導函數值恒為正值,而g(x)的導函數值恒為負值,不可能存在公切線;在兩函數交點的右側,由于g(x)圖象恒在f(x)圖象下方,所以也不可能存在公切線.綜上,當f(x)與g(x)的位置關系屬于圖7所表示的情況時,兩函數不存在公切線.
當函數f(x)與函數g(x)的圖象在y軸右側有共同切點的公切線時,設參數a的值為a0,當a≥a0時,f(x)與g(x)均存在公切線;當a 由點(1,y0)同在y=f(x)與y=g(x)上,得f(1)=g(1),即0=1+a0,解得a0=-1. 由圖象可知,當a≥a0=-1時,f(x)與g(x)存在公切線;當a<-1時,f(x)與g(x)不存在公切線. 綜上,a∈[-1,+∞). 點評:在求解參數范圍問題時,通常可以使用圖象法尋找臨界值進行求解,雖然在解答題中不夠嚴謹而存在瑕疵,但在客觀題求解中是常見方法. 鏈接1若直線y=kx+b是曲線y=lnx的切線,也是曲線y=ex-2的切線,則k=. 分析:分別設出直線與兩曲線的切點坐標,求出導數值,得到兩切線方程,再由兩切線重合得斜率和截距相等,從而求得切線方程. 鏈接2(2018年天津卷理科第20題)已知函數f(x)=ax,g(x)=logax. 分析:兩個函數的公切線問題可轉化為二元方程組解的問題,通過消元,將方程組化為方程.而方程是否有解的問題可歸結為連續函數的零點存在問題,即只要在區間上存在兩個自變量,其函數值異號即可. 證明:曲線y=f(x)在點(x1,ax1)處的切線l1的方程為y-ax1=(x-x1)ax1lna. 有解. 1-x1lna=x2lna(lnx2-1). 再由⑤得x1lna+lnx2=-2ln(lna),故有 1+2ln(lna)+lnx2=x2lna(lnx2-1). ⑦ 下證方程⑦有正實數解. 令r(x)=xlna(lnx-1)-lnx-2ln(lna)-1,則r(e)=-2ln(lna)-2≤0.那么由零點存在定理可知,只要找到一個x0>0,使r(x0)≥0即可.