源于教材 高于教材
——“長短弦定理”及其推論
?山東省德州市臨邑第一中學
劉文明 王志武
歷年來,在高考、模考中,以過圓錐曲線焦點的弦為背景的問題(簡稱焦點弦問題)層出不窮,經久不衰.比如,2022年全國新高考Ⅰ卷第16題,2022年山東臨沂一模第21題,2020年高考山東卷第13題,2018年新課標全國Ⅱ卷第19題,等等.很多專家學者也對焦點弦的性質進行了研究,但都用到了圓錐曲線的第二定義,如文獻[1]、文獻[2]等.由于2019年版新教材及更早的教材中已刪減了圓錐曲線的第二定義,影響了相關性質和結論的推廣和應用.為便于高中師生理解和接受,筆者避開第二定義,在橫向橢圓的基礎上利用高中知識對焦點弦的性質進行了研究,提出長短弦定理及相關推論.實踐證明,長短弦定理及其推論是解決焦點弦長度問題的有力工具之一.
1 角度式焦半弦公式
為了敘述的方便,我們把過圓錐曲線焦點的弦稱為焦點弦,焦點弦被焦點分成兩部分,每一部分都稱為焦半弦.
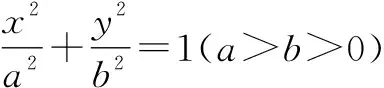
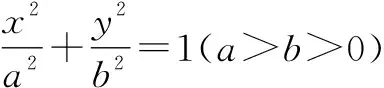
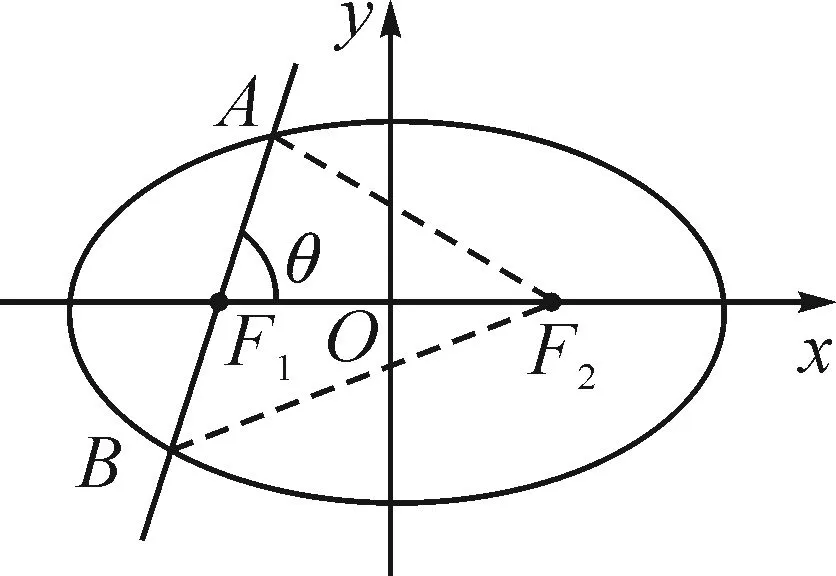
圖1
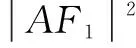
這個公式記憶的難點是分母中的正負號,其規律是上減下加.即對橫向橢圓來講,當弦AB過左焦點且點A在上方時,公式成立.
2 “長短弦定理”及其推論
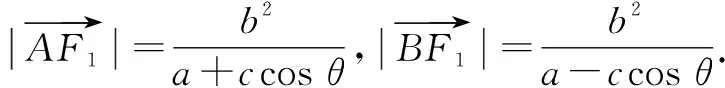

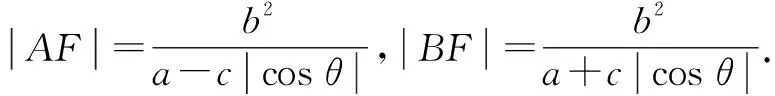
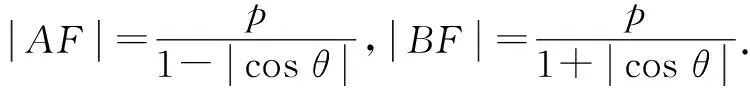
(注:這里a,b,c,p都是標準方程對應曲線的相關參數,以下同.)
由長短弦定理可進一步推演得如下推論成立.
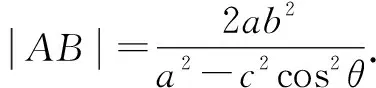
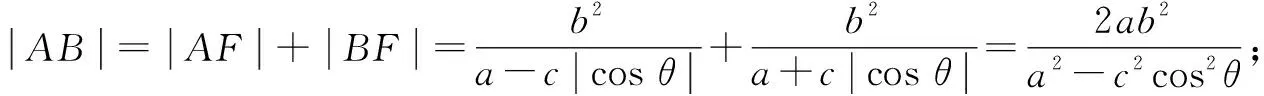
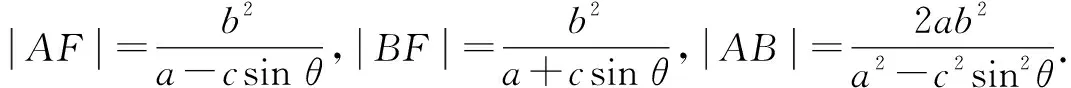
推論2證明從略.
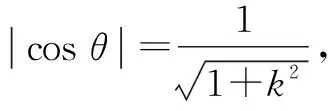
3 “長短弦定理”及其推論應用舉例
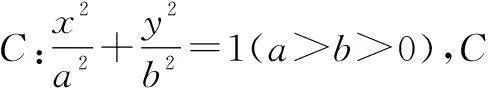
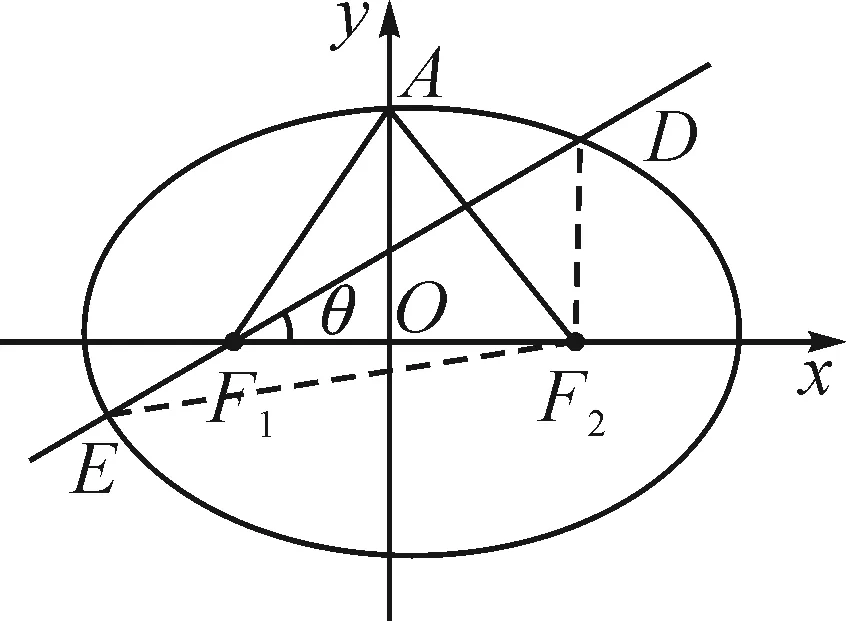
圖2
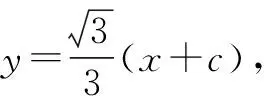
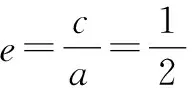
由“長短弦定理”,得
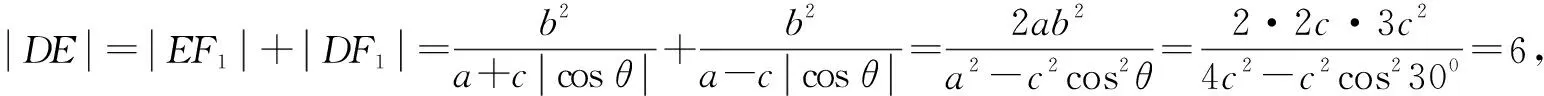
因為直線ED為線段AF2的垂直平分線,所以△ADE≌△F2DE,故△ADE的周長l=|DE|+|EF2|+|DF2|=4a=13.
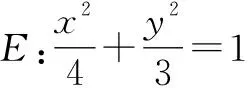
分析:傳統解法是先設出直線方程,與橢圓方程聯立消元,然后利用弦長公式表示出弦長,再進一步求值,這樣計算量大,冗長易錯,容易陷入小題大做的陷阱.兩種解法對比如下.
解法1:傳統解法.
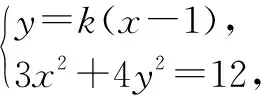
(3+4k2)x2-8k2x+4k2-12=0.
由弦長公式,得
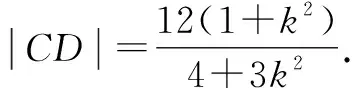
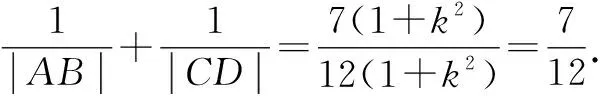
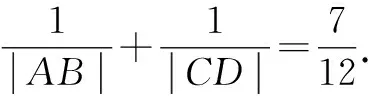
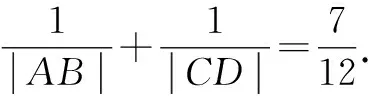
解法2:利用長短弦定理及其推論.
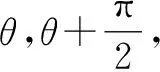
兩種方法對比,解法2計算量小,簡潔明快,節約時間.對于選擇與填空題,優勢明顯.
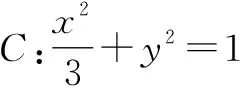
分析:本題的傳統解法是設出直線BF1的方程,然后與橢圓方程聯立消元,利用韋達定理及弦長公式、點到直線的距離公式等將四邊形的面積表示出來,再研究最值,這樣計算量大,繁瑣易錯.如圖3所示,延長BF1交橢圓于點A1,由對稱性可知|AF2|=|A1F1|,故AF2,BF1可以看作是同一焦點弦的兩個焦半弦,可借助長短弦公式求解,事半功倍.
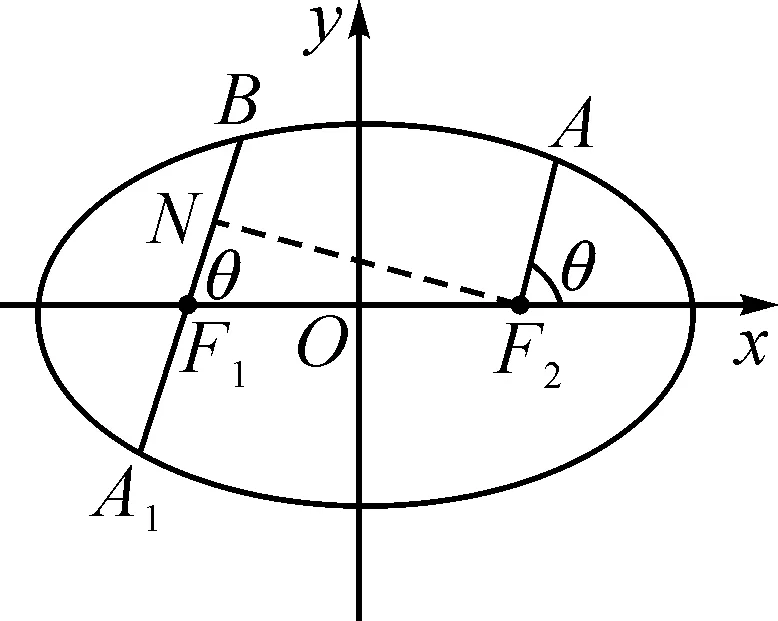
圖3
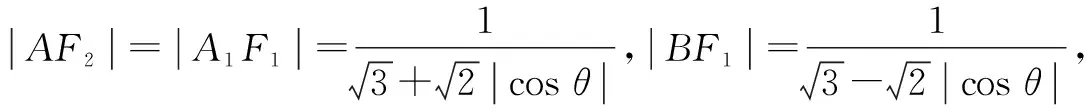
例4(江西省新八校2019屆高三第二次聯考)如圖4,過拋物線y2=2px(p>0)的焦點F的直線l交拋物線于點A,B,交其準線于點C,若|BC|=4|BF|,且|AF|=6,則p的值為.

圖4
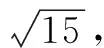
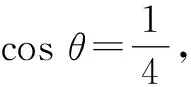
統計往年試題發現,與焦點弦長度有關的問題在高考、模考中出現頻率較高.高中階段解決焦點弦問題的傳統方法是將直線與曲線方程聯立,消元后得到一元二次方程,然后利用韋達定理及弦長公式求解,其實質是代數法,運算量與思維量較大,求解過程繁瑣耗時且易錯.而用“長短弦定理”及其推論處理與焦點弦長度有關的問題,其實質是幾何法,求解過程簡潔明快,思維量與計算量小,準確率高.高中階段適當拓展相關知識,有利于開拓學生思路,提高解題效率.

