巧借整體思想優化數學思維
錢 怡
?江蘇省常熟中學
在數學解題教學中,教師若僅就題論題,不關注問題的整體結構,將難以應對復雜多變的數學題.在數學教學中,教師要善于用典型的綜合題來引導學生運用適當的解題思路和解題方法來解決難題,進而讓學生擺脫枯燥的死記硬背和生搬硬套,提升學生的綜合能力[1].
利用整體思想從整體和大局出發,根據數學結構特征從整體去分析和思考,進而實現化繁為簡、化難為易的轉化,幫助學生厘清思維障礙,從而成功解決問題.
1 整體思想應用的重要性
首先,整體思想著眼于全局,重視整體的開發和改造,使題目經過開發和改造后結構特點更加清晰,使解題思路更加明朗,有利于解題效率的提升.
其次,運用整體思想解題時往往采用整體代入、整體換元等方法進行求解,使復雜的問題通過構造和轉化變成了一個整體,這在優化解題步驟、優化數學思維上都是一個較大的提升.
最后,整體思想作為常用的解題技巧,在高中數學中被廣泛地應用,如幾何證明、代數式的求值等,可以幫助學生厘清解題思路,使解題變得游刃有余.
2 整體思想應用面臨的問題
運用整體思想解題需要學生具有較強的分析能力、構造能力和推理能力,而這些能力往往是學生較為欠缺的.究其原因主要是在日常教學中,學生習慣于“灌輸式”的強化訓練,習慣于就題論題,缺乏整體的建構能力和分析能力,因此在遇到利用整體思想來解題的問題時顯得力不從心,整體思想的應用步履維艱.基于此,教師的教學形式和學生的學習形式都應該有所改變,應使教學由“重知識”向“重能力”轉化,使學習由“被動學”變為“主動思”.
在教學中,教師要仔細分析教材,研究章節間的聯系,善于從整體出發,讓學生先對相關知識點有個大輪廓的了解,之后再從局部出發進行知識的內化,以此引導學生從宏觀上去把握知識,樹立宏觀意識,為知識體系的建構奠定基礎.
3 整體思想應用的教學實踐
3.1 整體代入
高考主要考查學生的綜合能力,高考中若出現代入法求值的問題時,往往不是簡單代入就可以直接求解的,其主要考查的應是學生的整體代入思想,因此若在求解時發現其計算量大或很難求解,就必須對比已知和結論,從已知和結論中找到聯系,進而通過整體代入實現化難為簡.
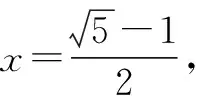
分析:如果求解時直接應用代入法,雖思路簡單但求解困難,故該方法不可取.
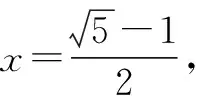
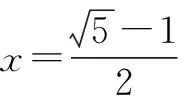
3.2 整體換元
換元是數學解題的常用手段,通過換元可以實現降次、化分為整、化繁為簡的目的,其在方程、函數、三角問題中的應用較多.
例2求函數y=sinxcosx+sinx+cosx的最大值.
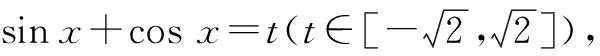
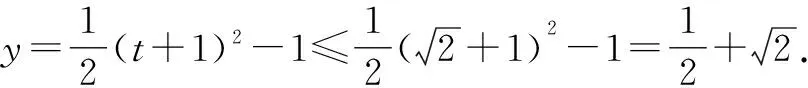
評注:此題是利用sinx與cosx的平方關系,將sinx+cosx看成整體,令sinx+cosx=t,通過換元和轉化,使之成為二次函數求最值的問題,從而實現了化繁為簡.
3.3 設而不求
“設而不求”是整體思想的重要應用,運用該方法可以將學生從復雜的運算中解放出來,通過整體分析、聯想輕松地解決問題,從計算求解升華至分析求解,有利于解題思路的優化.
例3過圓外一點P(a,b)引圓x2+y2=R2的兩條切線,切點分別為A,B,求直線AB的方程.
根據已知條件求兩切點所在的直線方程首先想到的就是兩點式,但求兩切點坐標非常復雜,故教師帶領學生選擇了其他解決方法.
師:若不求切點A,B的坐標,根據已知條件你能寫出兩切線的方程嗎?(小組合作求解)
生1:設兩切點為A(x1,y1),B(x2,y2),則切線方程為x1x+y1y=R2,x2x+y2y=R2.
師:根據已知,兩切線過點P(a,b),則有x1a+y1b=R2,x2a+y2b=R2.根據以上信息你能寫出直線AB的方程嗎?
學生通過觀察,得出直線AB的方程為ax+by=R2.
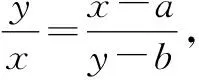
上述兩種解法都應用了“設而不求”的整體思想,通過“設”為已知和未知架橋鋪路.通過整體觀察、分析,規避求解的過程,這樣既節省了時間又避免了解題過程中可能產生的錯誤,有利于提高解題準確率.
3.4 整體構造
數學題目具有一定的結構特征,有些結構是“顯性”的,學生可以直接利用原有認知進行求解,而有些結構是“隱性”的,需要結合已有經驗進行轉化才能轉變為學生熟悉的數學模型.對隱性特征的轉化需要學生從整體去發現、構造.
例4sin20°cos70°+sin10°sin50°的值是( ).
題目乍看上去應該是應用正余弦的和或差公式求解,然仔細分析卻不能直接應用,若進一步轉化合并求解則會大大地增加計算量.根據題目特點可以嘗試應用構造法求解.
解:設a=sin20°cos70°+sin10°sin50°,b=cos20°sin70°+cos10°cos50°,則
a+b=sin90°+cos40°=1+cos40°;
評注:因本題缺乏直接應用公式的條件,但已知條件是對稱的,故可通過構造b使之與公式建立聯系,進而整體求解,使解題獲得了事半功倍的效果.
3.5 整體聯想
整體聯想主要考查的是學生的思維能力和思維習慣,通過聯想、分析,實現問題的轉化,從而拓展解題思路,提升解題效率.
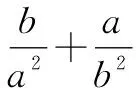
依據常規解題方法應先求出a,b的值,然后分四種情況進行討論,運算量較大,容易出現錯誤,故可嘗試從整體入手分析.
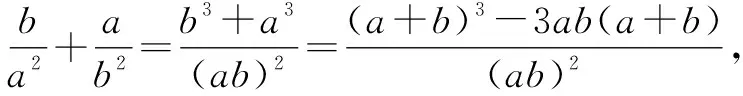
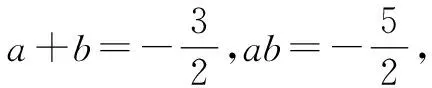
評注:求解時從結論入手,將結論進行通分轉化,通過觀察、分析、轉化,發現將a+b和ab分別看成整體,利用根與系數的關系進行求解,可避免繁瑣的分類討論,既節省了解題時間又優化了解題步驟和思路.
總之,數學題目多變,數學解題方法亦是如此,在解題時要避免就題論題的生搬硬套,要善于培養學生的觀察能力、分析能力和總結歸納能力,進而從重知識向重技能轉變,以此來提高解題能力,優化思維結構,提升創造力.

