目標意識在數學解題教學中的培養策略*

劉遠來 李紅梅

?西華師范大學

目標意識是指一種由主體依據解題目標，分析條件和作用、結論和等價關系，有目的地將條件和結論相關聯的思維活動.其中解題目標可分為中間目標和最終目標.目標意識的培養有助于學生明確解題方向，探尋解題切入點，構建解題系統.

著名數學家波利亞在《怎樣解題》中說：我們喜歡朝著目標直接走，對于繞著走、反著走、或者脫離目標有一種心理上的反感.由此可見目標意識的重要性，目標意識對于解題起著導向性作用.而現在中學生由于思維水平、認知結構的局限性，在難題的處理上缺乏目標意識，找不到破題口.基于在解題教學中如何引導學生解題，培養學生核心素養，避免學生在解題過程中的盲目性，筆者從目標意識入手，從以下三個方面淺談目標意識的培養策略.

1 活用化歸思想，明確解題方向

化歸思想是指復雜問題通過某種變換轉化為簡單問題，未知問題轉化為己知問題的過程，達到化生為熟，化難為易，化繁為簡，化迂為直的目的.運用化歸思想，對題目的解題目標進行變換，明確解題的方向，增強學生解題的目標意識，在化歸中培養學生創新性思維.

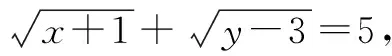
分析：這是一道根據等式限制條件求取值范圍的題目，如果運用常規思路用一個變元表示另一個變元，計算過程較為復雜，也不易求解.下面利用化歸思想架構知識之間的聯系，變換解題目標，明確解題方向.

根據化高維為低維的劃歸思想，采用換元法進行化歸：

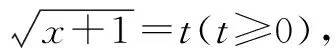
所以2x+y=2(t2-1)+(5-t)2+3

=3t2-10t+26(0≤t≤5).

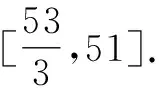
2 借助逆向思維，探尋解題切入點

逆向思維是一種思想(概念、原理、觀念)反過來思考的思維方式.具體而言，是把題目中的結論當作條件，并結合題設部分條件，通過轉化、推理，得到一個顯而易見的結論.通過這種思維方式得到的結論就是探尋解題切入點的關鍵.逆向思維不僅在利用定義、運算法則、定理進行解題時經常使用，而且對于幾何、不等式和導數的相關證明也有妙用.

例2若a,b,c是不全相等的正數，求證：

分析：該題是一道證明不等式恒成立的問題，但是利用顯性題設條件很難證明結論，不易探尋解題的目標切入點.下面通過逆向思維來分析試題，并展現目標意識的思維過程.

3 巧用概念圖，構建解題系統

概念圖是組織知識和表征知識的工具，包括概念或命題間的相互關系，概念通常置于圓圈或方框中，用連線及其連接語表明兩概念間的聯系.

對于一個初始條件復雜、結論較為抽象的問題，我們往往難以入手，目標迷茫，想不到破題的關鍵.我們不妨引入概念圖厘清條件和結論之間的關系，構建解題的層級目標，形成解題的目標系統.繪制數學概念圖，有利于提高學生發現問題、提出問題、分析問題、解決問題的能力，有利于培養學生邏輯推理和直觀想象核心素養，有利于提高學生思維的系統性、廣闊性、深刻性，為數學解題目標意識的培養提供了一種思維工具.

構建概念圖的流程如下.首先，將解題的結論作為最終目標；其次，分析題目中每個條件的作用及其相互關聯關系；然后內化條件，相互轉化，推理出所需的中間目標，并用箭頭進行有意義連接，標注好兩個目標之間的關系；再次，厘清各個過渡目標的內外層級、因果關系，形成一個完整、邏輯清晰的概念圖；最后，對所構建的概念圖反思每個過渡目標的確定是否合理、正確，每個目標之間的意義連接是否有用.

例3已知函數f′(x)是奇函數f(x)(x∈R)的導函數，當x<0時,xf′(x)+f(x)>0,且滿足f(-2)=0,則使f(x)>0成立的x取值范圍是( ).

A.(-∞,-2)∪(0,2) B.(-2,0)∪(2,+∞)

C.(-∞,-2)∪(2,+∞) D.(-2,2)

根據例3題設條件，繪制概念圖需要確定以下幾個中間目標.

目標一：這是一道結合導數知識的不等式抽象函數問題，這類問題的解題策略是什么？

在數學解題中注重通性通法.這類問題的解題策略往往是利用函數單調性脫去“f”的方法，將抽象函數不等式轉化為具體函數不等式，進而利用不等式性質求出未知數的取值范圍.因此，這是我們解題的總體目標，為解題確定了方向.

目標二：根據條件x<0,xf′(x)+f(x)>0,我們可以關聯到哪些知識點，對解題有何作用？

可以聯想到函數F(x)=xf(x)的導函數為F′(x)=xf′(x)+f(x),利用逆向思維構造函數F(x)=xf(x)，那么導函數的單調性迎刃而解.在此過程中xf′(x)+f(x)>0,決定了導函數的正負性，進而確定了F(x)的單調性，是解題的關鍵之處.

目標三：根據條件“函數f′(x)是奇函數f(x)(x∈R)的導函數”，從函數的奇偶性考慮，F(x)與f(x)有什么關系？在探尋解題目標的過程中有何作用？

f(x)的奇偶性決定了F(x)的奇偶性，F(-x)=-xf(-x)=xf(x)=F(x),因而F(x)是偶函數.而目標二只能確定(-∞,0)上函數圖象的變化趨勢，當確定了F(x)是偶函數，(0,+∞)上的函數圖象變化趨勢便一目了然.

目標四：條件f(-2)=0的作用是什么？

作用有三：其一是確定了構造的函數的零點，分割清楚函數值的正負范圍；其二是得到了f(2)=0；其三是為了將f(x)>0等價變形為f(x)>f(-2)，或f(x)>f(2).

目標五：如何由F(x)>0來確定f(x)>0的取值范圍？

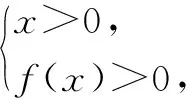
由上述確定的五個中間目標繪制如圖1所示的概念圖.

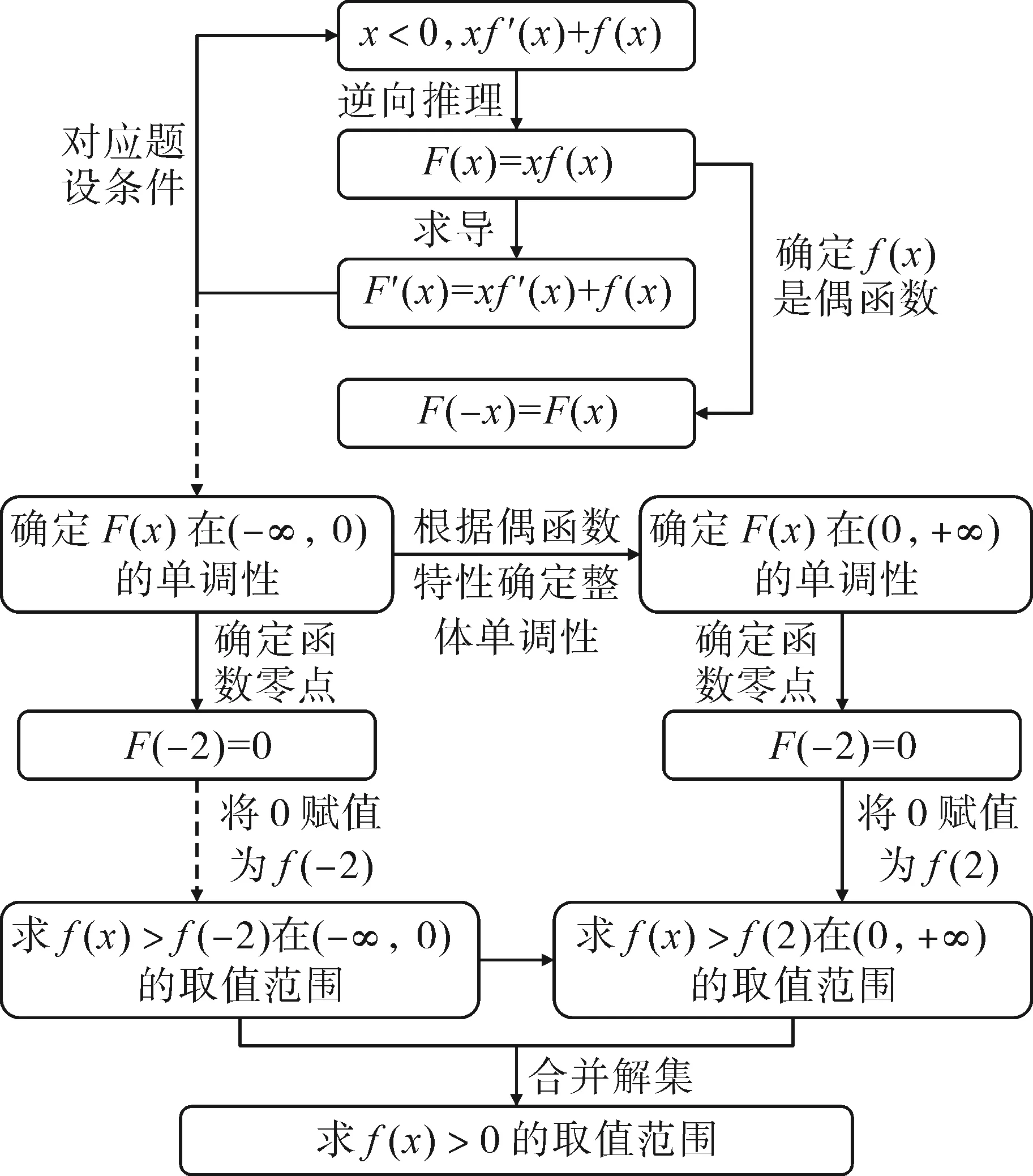
圖1

問題是數學的心臟，數學問題的解決是培養學生數學核心素養的重要成分.由上述分析可知目標意識在解題中發揮著舉足輕重的作用.加強學生解題的目標意識，從多角度、多途徑進行培養，并考慮學生自身情況，因材施教.這樣,學生在解題時才能做到積極思考和主動探究，提高數學解題能力，抓住數學本質,引導學生會用數學的思維思考現實世界.