“天問一號”火星探測器著陸控制方案研究

阮吉利，李洪軒，邱科悅，郝立麗

（東北林業大學，黑龍江 哈爾濱 150040）

“天問一號”火星探測器于2021年5月中旬在火星烏托邦平原上順利著陸，我國首次火星探測任務取得了巨大的成功。在此之后，“祝融號”火星車將對著陸點依次執行全球成像、自我檢查、脫離著陸平臺和巡邏檢測等工作[1]。“天問一號”的成功著陸，是我國航天事業特別是行星探測領域發展的又一個里程碑，同時也表明我國成為世界上第二個著陸火星的國家。本文收集關于火星探測器的信息資料，就“天問一號”的著陸過程建立模型，基于時間最短、能耗最少的原則，對操控方案進行設計，并結合實際情況對操控方案進行檢驗。

1 “天問一號”著陸過程耗時最短控制策略分析

1.1 “天問一號”落火過程分析

搜集相關信息后，本文將“天問一號”著陸過程簡化為以下5個階段。

第一階段：兩器分離段。探測器于火星停泊軌道上運動，尋覓到合適的著陸時機后通過發動機點火減速降軌。降低到一定高度后，探測器分離為環繞器與著陸器，著陸器向火星墜落；環繞器則在分離半小時后點火加速升軌，返回停泊軌道。

第二階段：氣動減速段。著陸器進入火星大氣后，受到空氣阻力的影響，速度大幅減小。

第三階段：傘系減速段。著陸器打開降落傘，由于降落傘與空氣的接觸面積較大，空氣阻力大，能有效減小著陸器的速度。

第四階段：動力減速段。探測器通過發動機點火的方式進一步減小了速度。

第五階段：懸停避障與緩速下降段。在高度降為100 m時，探測器的速度基本降到0。探測器懸停避障，尋找最安全的著陸地點，最后通過4個著陸腿的緩沖作用在火星表面軟著陸。

1.2 模型建立

為設計控制方案使得著陸的時間最短，主要控制3個環節：環繞器與著陸器分離；打開阻尼傘的時機；發動機點火的時機。3個環節息息相關，必須綜合決策。查閱資料可得：近火點高度Hc=280 km；遠火點高度Hf=59 000 km；火星平均半徑R=3 397 km；軌道為橢圓。決定著陸前，探測器將環繞火星運動。

1.2.1 環繞器與著陸器的兩器分離段

設探測器在距離火星h1時進行減速降軌，根據近火點高度Hc和遠火點高度Hf可得280 km＜h1＜59 000 km。探測器在發現合適的著陸時間后，通過發動機噴氣減速。為了簡化問題的分析，假設這一減速過程所需時間可忽略不計。

根據萬有引力定律F萬=mg，火星重力加速度為其中m為“天問一號”在各個階段的質量；M為火星質量；G為引力常量。但由于探測器距離火星的高度相對于火星半徑不可忽略，則探測器在距離火星h1處的火星重力加速度為

為方便計算，本文取g″為降軌時探測器所處高度重力加速度與到達火星大氣時重力加速度的平均值，即

式中：h2為火星大氣層距離火星地面的高度。

探測器沿著切線方向具有初速度，且該速度小于火星的第一宇宙速度。而在靠近的過程中，探測器將分離為環繞器與著陸器，環繞器通過加速升軌，不影響著陸器的運動。綜上，可將探測器進入火星大氣前的運動視為平拋運動。

根據動能與勢能的轉換公式，動能為

式中：v0為垂直火星方向上探測器的速度；h=h1-h2。從而推出著陸器進入火星大氣時，探測器在豎直方向的速度為

探測器降軌到進入火星大氣耗時t0為

1.2.2 氣動減速段和傘系減速段

進入火星大氣后，“天問一號”主要受重力和空氣阻力。著陸器進入火星大氣后，高度對重力加速度的影響可以忽略不計，因此，取重力加速度g=3.71 m/s2；著陸器所受重力即為G1=mg。

設著陸器進入火星大氣后，經過時間t1打開阻尼傘，傘降時間t2后進入動力減速段。為得到著陸器在氣動減速段、傘系減速段中，其位移與時間的關系，本文做了如下嘗試。下面為便于公式的書寫，令則空氣阻力F=kv2。

在氣動減速段，著陸器在下落過程中只受到重力和空氣阻力的作用，且重力的方向與空氣阻力的方向相反。由牛頓第二定律mg-kv2=ma，可得出

通過一定的轉化，可將該方程式（6）轉化為黎卡提方程[2]，從而解得

由于著陸器長、寬各約4 m，底盤是圓形[3]，因此迎風面積S1約為12.56 m2；火星大氣的空氣密度ρ為0.015 8 kg/m3[4]；空氣阻力系數C為1.5。因此，上文設定的

在氣動減速段，著陸器進入火星時的初速度即為兩器分離段的末速度。

經過時間t1后，著陸器的速度為

著陸器的運動路程為

與氣動減速段類似，在傘系減速段，著陸器同樣做變加速運動，主要區別在于傘系減速段中著陸器展開的降落傘增加了著陸器與空氣的接觸面積，故k值發生了改變。此時，降落傘面積S2為300 m2，ρ與C保持不變，計算得

同理，這一階段（傘系減速段）的初速度為上一階段（氣動減速段）的末速度，經過時間t2后，著陸器的速度為

著陸器的運動路程為

1.2.3 動力減速段

考慮到“天問一號”在動力減速段已經接近火星表面，且速度比前幾個階段較低，因此該階段忽略火星大氣阻力對著陸器的影響[5]。

在動力減速段，著陸器扔掉大底和背罩，發動機點火向地面噴氣，通過反推力減速，著陸器共有27臺發動機，包括20臺250 N、6臺25 N和1臺7 500 N的發動機。故著陸器的最大推力為12 650 N。

達到動力減速段時，著陸器的速度為v2，其在最大推力的情況下加速度為

由于動力減速段著陸器為了懸停，末速度必須為0，因此動力減速段所用時間著陸器在動力減速段經過的位移x3為

1.3 模型求解

該模型得到的方程組約束條件是決策變量的非線性表達式，故利用MATLAB軟件編程，先使用蒙特卡羅模型獲得決策變量的初始值，再使用非線性規劃模型進行最優化求解[6]。目標函數為

其約束條件為

式中：h=h1-h2，火星半徑R=3 397 km；火星上的重力加速度g=3.71 m/s2；k1=0.149；k2=2.830；探測器與火星的距離h1為自變量；火星大氣層高度h2=125km。不考慮燃料質量，著陸器質量m=1 285 kg，模型求解步驟如下。

1）通過蒙特卡羅模型模擬，在給定決策變量范圍內生成1億組隨機數，從實驗點中找到可行點。

2）通過“打擂臺”思想，從可行點中找出最小可行點x0，得h1=5 967.365 km；t1=285.77 s；t2=74.68 s；t3=67.43 s。

3）再將得到的x0代入非線性規劃模型，分別通過內點法、序列二次規劃法、有效集法和信賴域反射算法4種算法，搜索尋求最優的決策變量。

4）通過比較4種算法獲得的最優決策變量，選取更優解。

5）最終選取內點法獲得的決策變量。得到h1=6 135.637 km；t0=2 505.3 s；t1=263.67 s；t2=73.23 s；t3=64.65 s；z=2 906.85 s。即“天問一號”著陸過程的最短總時長z為2 906.85 s。

2 “天問一號”著陸過程耗能最少控制策略分析

2.1 模型建立

該處主要探討在給定的著陸時間下，著陸器耗能最少的方案，故假定著陸器從降軌到進入大氣的持續時間t0、氣動減速段持續時間t1、傘系減速段持續時間t2均為已知量。

通過對探測器著陸各個階段的研究，本文認為能量消耗的主要階段為降軌減速段以及進入火星大氣后的動力減速段。

2.1.1 探測器降軌減速段

當探測器在火星停泊尋找到合適的著陸時機后，發動機將點火制動，減小速度以實現降軌。在該階段中，發動機點火消耗的能量等價于探測器動能的變化量。

根據動能定理，該階段著陸器消耗的能量為

為使能量消耗最少，vt應該盡量大；但同時vt又應該小于火星的第一宇宙速度，否則著陸器將無法墜向火星，故取

依據著陸器從降軌到進入大氣的持續時間t0，可知探測器降軌時的停泊軌道距離火星大氣的高度由此可得探測器距離火星的距離h1=h0+h2=h0+125 m。

由開普勒定律，任何橢圓天體軌道的中心天體一定在橢圓的一個焦點上。同時根據橢圓的定義b2=a2-c2，得出方程組為

聯系萬有引力定律與牛頓第二定律，可以列出“天問一號”在近火點和遠火點的運動學方程組為

式中：vc和vf分別為著陸器在近火點的速度和在遠火點的速度；ρc與ρf分別為近火點和遠火點的曲率半徑，聯立以上各式，代入參數，得近火點速度vc=4.691 5×103m/s，遠火點速度vf=890.538 2 m/s。

根據開普勒第二定律可得

根據能量守恒定律可得

由此得著陸器在火星海拔h1上的速度v0為

2.1.2 動力減速段

著陸器在進入大氣后將先后經過氣動減速段、傘系減速段以及動力減速段。

根據傘系減速段的運動規律，著陸器受到的空氣阻力與其運動方向相反，且該阻力的值與速度的平方成正比。因此，起初著陸器受到的空氣阻力大于其重力，著陸器做減速運動。而空氣阻力的值隨著速度的減小而減小，直到與重力達成平衡，著陸器將近似做勻速運動[7]。由于t0、t1為已知量，因此根據式（8）可以算出著陸器做勻速運動時的速度，不妨令其為v。

在傘系減速到某一高度后，著陸器將通過發動機點火來實現減速。假設著陸器在距離火星地面高度為h3時開始進行動力減速，此時速度為v，為了進行后續的懸停避障，在距離地面高度為100 m時著陸器速度應減小為0。根據能量守恒定律，在動力減速段中，發動機所做的功為

設發動機推力為F推（0 N＜F推＜12 650 N）。動力減速段，豎直方向上著陸器受重力以及發動機推力。因此，著陸器在動力減速段做勻減速運動，加速度為

為滿足著陸器距離地面100 m時懸停的條件，可得

2.2 模型求解

2.2.1 降軌減速段求解

在探測器的降軌減速段，本文通過開普勒定律、牛頓第二定律等對探測器在火星停泊軌道上的運動做了分析，在著陸器從降軌到進入大氣的時間已知的前提下，推導出了探測器降軌時的速度。并在基于能量消耗最小化的考量下，得到了探測器降軌前后的速度，從而利用動能定理得到了降軌減速段的能量消耗。

整理相關公式可得方程組為

此處取t0為1 000 s，解得v0=4.396 3×103m/s；E1=1.678 2×107kJ。

2.2.2 動力減速段求解

有關動力減速段所描述的問題，可由一個有約束條件的線性規劃問題解釋。因此，本文用遺傳算法對本問題的模型進行求解[8-9]。

目標函數為

其約束條件為

模型求解步驟如下。

1）將決策變量排列為1個個體，初始種群由2 000個隨機產生的個體組成。

2）編寫適應函數，來計算個體的性能指標。

3）選擇出指標較好的個體留存，并遺傳給下一代。

4）隨機將個體兩兩配對，并按照規定的交叉概率進行交叉。

5）若最大進化代數達到了20 000，則進行最優解的輸出；否則繼續進行編碼、評價、選擇、交叉等操作。

通過約束條件的分析，本問題的模型確定了交叉概率為0.6。對模型進行求解，得到v取90 m/s時，h的最優解為660.21 m。此時，由于E2=8 351.702 kJ，因此E=E1+E2=1.679×107kJ。

3 “天問一號”著陸模型與實際情況的匹配度檢驗

探測器的著陸數據如下。

1）兩器分離段結束，著陸器飛行3 h后進入火星大氣（火星大氣層高度為125 km）。

2）氣動減速段：著陸器在約290 s內，將速度從4.8 km/s減速到460 m/s。

3）傘系減速段：在距離火星地面11 km左右處，探測器打開降落傘，在約90 s內將速度由460 m/s降至95 m/s。

4）動力減速段：距離火星地面1.5 km左右處，探測器通過發動機進一步減速，用80 s左右的時間將速度減小到3.6 m/s。

5）著陸緩沖段：在距離火星表面約100 m時，著陸器的速度基本降為0。

前文對著陸器的著陸過程建立了運動模型。為驗證與評估該模型的科學性，本文代入3個參數值：進入火星大氣時的速度（4 800 m/s）、氣動減速段持續的時間（290 s）、傘系減速段持續的時間（90 s），則用于求解的方程組為

解得氣動減速段的位移為103.120 1 km，傘系減速段的位移為11.642 2 km，動力減速段的位移為1.337 7 km。對比“天問一號”著陸時在這3個階段的實際位移114 km、9.5 km、1.5 km，利用公式求得相對誤差分別為9.54%、22.6%、10.82%。其中，Er為相對誤差；T為真實值。由此可知，本文建立的模型與實際的著陸過程存在可忽略不計的誤差。

隨后，本文取10組著陸器進入火星大氣時速度與氣動減速段持續時間的數據，代入模型運算，得到氣動減速段的位移，對取得的數據擬合后，得到計算值與真實值的擬合圖（見圖1）。

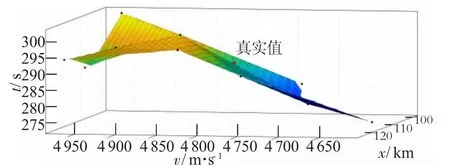
圖1 計算值與真實值的擬合圖

由圖1可知，真實值與擬合所得曲面的計算值較為接近。綜上，可認為本文對于著陸過程所建立的運動模型與實際情況較相符，準確度較高。

4 結論

本文通過數學和物理方法，對“天問一號”探測器著陸的各個過程進行分析，建立運動模型方程。首先，以著陸時間最短為優化目標，明確自變量、約束條件后，建立了單目標優化模型，用非線性規劃模型進行最優化求解，解得著陸的最短總時長為2 906.85 s。其次，在給定著陸時間的前提下，建立以能量消耗最小為目標，以發動機推力、點火時間為自變量，以著陸器在火星海拔100 m時速度為0為約束條件的優化模型，并利用遺傳算法進行了規劃求解，解得在確立各個階段用時的前提下，著陸最少消耗能量為1.678 2×107kJ。最后，為檢驗運動模型的準確性，本文搜集了“天問一號”著陸的真實值數據，代入模型計算后發現誤差較小，具有一定可信性。