數學學習個體差異成因分析與應對措施的研究
江蘇省南通市小海中學
季 霞
教學中,學生獲得的知識量與學習效率有著很大的關系,而影響學習效率的因素多且復雜.其中,個體差異是影響學習效率的重要因素之一.數學教育一直倡導“因材施教、學有特色、鼓勵冒尖、允許落后”等理念,就是考慮到學生與學生之間存在著一定的個體差異.因此,筆者特針對個體差異的主要成因進行了研究,并結合自身的教學經驗,提出應對措施.
1 個體差異的成因分析
1.1 智力差異
智商是判斷學生智力發展的基本標準,包括超常、正常與低常三類.一般我們將智商得分超過130分,稱為超常;90~110分,劃為正常范圍;低于70分,稱為低常[1].智商雖然基本趨于穩定狀態,但受教育、環境以及個體主觀因素的影響,智商可以發生一定程度的變化.由此也可以看出,社會環境、教養方式、教育模式等對智力發展都有一定的影響.
1.2 認知差異
學生長期受生活背景與教育背景的影響,會形成不一樣的認知方式,主要表現在場依存性與場獨立性兩方面.認知方式是指個體接受學習信息的過程中,所釋放出來的差異性信息,是個人在記憶、感知與思考中,習慣性的一種偏好、態度與風格.
具備場依存性特征的個體,在認知行為表現中,常傾向于依賴外在的參照物,自我主觀能動性差,無法對外源性信息進行合理加工;而場獨立性個體,則很少受外界客觀因素的影響,具備良好的主體傾向,能自主加工、分析外來信息.場依存性與場獨立性特征為人類認知的兩個極端,大部分學生的認知介于這二者之間.
1.3 結構差異
從人類智力組成類型來分析,各種心理能力的組合與使用具有一定的差異性與復雜性,主要表現在:有的學生偏向于文科,有些學生偏向于理科,也有少部分學生文、理交叉發展;有人習慣性地應用左腦,有人習慣性地應用右腦,也存在左右腦平衡發展的學生;有些學生比較擅長形象思維,有些學生習慣抽象思維,也有學生兩類思維均衡發展;還有智力與非智力因素的差異等.
2 縮小個體差異的措施
個體差異除了受以上幾類因素影響之外,還受遺傳、教育環境、教學內容等多種因素影響.結合學生身心發展特征,筆者針對如何縮小個體差異做了大量實踐與研究,并取得了一定的成效.
2.1 結合學情,制定目標
張奠宙認為:將知識的學術形態轉化成教育形態是實施教學的首要任務.制定課程目標是教師實施課堂教學的第一步,將知識從學術形態轉化成教育形態,需要在深入了解學情的基礎上,結合教學內容,制定合理、可行的教學目標.而學生存在個體差異是每個教師需面對的現實,基于這種差異,制定層次清晰的教學目標,能讓每個層次的學生都能獲得學習帶來的成就感,從而對數學學習產生信心.
案例1“菱形的性質”的教學目標
知識技能目標:掌握菱形的概念與性質.
過程與方法目標:引導學生經歷菱形概念的形成過程,在觀察與分析中對菱形性質產生深刻理解,形成良好的思維意識,感知幾何說理的方法等.
情感態度與價值觀目標:培養學生形成主動探究與合作交流的習慣,為獲得嚴謹的思維奠定基礎,提升數學審美與價值觀.
以上三點雖涵蓋了新課標所提出的三維目標,看似完整,卻存在維度割裂、抽象籠統等問題.該目標的制定明顯違背了三維目標的實質,也沒有結合學生的實際情況.課時目標應比課程目標更加具體、入微,應涵蓋教學活動落實的基本任務與學生經學習后具體達到的深度.
尊重個體差異的目標應具有層次性、完整性、融合性、具體性.如本節課的教學目標可作以下調整:
(1)以平行四邊形的特殊化性質,推導出菱形的概念、性質,感知菱形與其他類似圖形的異同點;
(2)親歷菱形性質的探索,積累研究幾何圖形性質的經驗,強化從特殊到一般的數學思想方法,驅動邏輯推理能力的發展;
(3)通過對菱形性質的探索與應用,體悟數學思維的周密性與嚴謹性,感受學習帶來的成就感,樹立學習信心.
經調整后的教學目標,更加具體,且結合了每個層次水平學生的認知需求,學生依照自身的實際情況,對照著教學目標參與學習,可獲得良好的情感體驗.
2.2 夯實基礎,培養習慣
有些基礎較薄弱的學生,反應總要慢半拍,推理能力也嚴重不足.對于此類學生,教師可以基礎為抓手,著重培養學生的學習習慣.
(1)聽課習慣
據調查,大部分學生的智力水平并沒有太大差異,但學習習慣的差異,導致了學習效率的巨大差別[2].培養良好的課堂聽課習慣,對提高學生的學習效率具有舉足輕重的影響.尤其是一些基礎薄弱的學生,存在上課聽不懂,課后什么都不會的狀態.作為教師,應多關注這一類學生,在課堂上盡可能設置一些簡單的問題讓他們回答,以增強這類學生的信心.
(2)書寫習慣
規范的書寫不僅能培養規范答題的習慣,還能為復習奠定基礎.這里所說的數學書寫習慣,主要包括重點知識與經典例題的筆記,尤其是常用的公式、定理與法則等,必須嚴格、規范地書寫,這樣才能確保應用與運算時的準確.不少學生在考試中出現丟分現象,就是由于書寫潦草、不規范而出現令人痛心的失誤.
(3)運算習慣
培養良好的運算習慣,是縮小個體差異的重要方法之一.有些學生雖然具備良好的解題思維,卻缺乏嚴謹的運算習慣.當碰到常規的去括號、合并同類項等計算時,頻頻出錯,導致與同伴的差距越來越大.初中階段的運算,要求學生盡可能不要跳步,更不要簡化步驟.
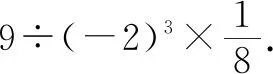
(4)歸納習慣
數學作為一門系統性的學科,各個章節的知識點之間都存在某種意義上的聯系.學生在學習過程中,應養成定期總結與歸納的習慣,尤其是公式、定理、法則、數學思想方法等,經整理后,更加利于記憶.有些學生對于教師講了幾遍的知識,還是記不住,其實這并不一定是智力因素,很大一部分原因在于學生自己沒有形成總結、歸納的習慣[3].實踐證明,良好的歸納能力能有效地增強記憶.
案例2“有理數”的教學
學生初次接觸有理數,覺得很繁雜,若學會分類整理,則便于理解性記憶.
(1)按有理數的意義分類,如圖1所示.

圖1
(2)按正、負來分,如圖2所示.

圖2
將有理數按照意義與正負來分類,在此基礎上再進行總結,則能讓學生對本章節內容產生直觀、形象的理解,為后繼學習奠定基礎.
2.3 問題驅動,發展思維
數學是思維的體操,發展學生的數學思維是縮小學生個體差異的關鍵性因素.問題是數學的核心,是促進思維發展的根本,思維一般是從問題開啟的.因此,精心設計問題,能有效地開啟學生的思維,推動學生主動思考.
案例3“勾股定理”的教學
問題1從教室到操場,走哪條路最近?
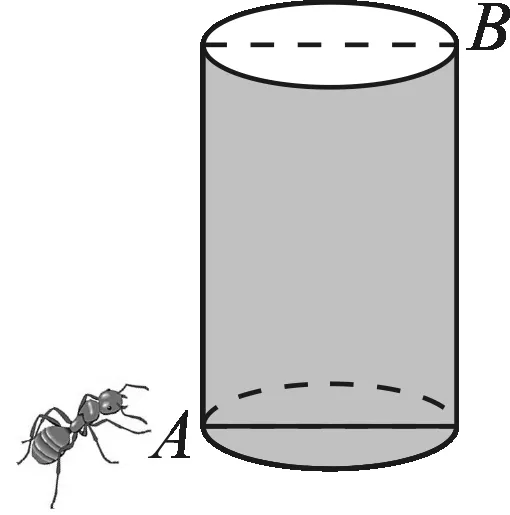
圖3
問題2如圖3,小麗在公園的圓柱形石凳上點B處遺留了一些餅干屑,一只螞蟻在地面點A處捕捉到了這個信息,便準備爬上去獲取食物,想要路程最近,該如何爬行?
問題1引導學生復習了兩點間線段最短的知識,問題2則有效地激發了學生的探究熱情,驅動了思維的活動,為本節課的教學奠定了良好的基礎.
蘇霍姆林斯基提出:要讓每個孩子昂首挺胸地走路.只要教師將日常教學工作做細、做實,培養學生的學習習慣,讓學生能自主解決生活、學習中的困難,終能將個體差異中的不利因素轉化成有利因素,使得每個學生都能在數學學習中獲得長足的進步.

