例析求分式值的幾種常用方法
甘肅省白銀市白銀區(qū)武川新村學校
王花香
分式的計算是“認識分式”這一章中的重點,而求分式的值是分式的計算中的重點.由此可見,掌握求分式的值的方法,對提高學生本章知識點的掌握程度和應(yīng)用能力具有積極意義.所以,本文中在舉例分析的基礎(chǔ)上,利用舉一反三或變式等方法,呈現(xiàn)求分式的值的幾種常用方法,以期幫助一線教師不斷提高課堂教學效率.
通過對近幾年各地中考數(shù)學試卷的分類整理發(fā)現(xiàn),求分式的值多以解答題形式出現(xiàn),在某些省市區(qū)的試卷中也會以選擇、填空題的形式出現(xiàn).下面,筆者采用例題分析的方式展現(xiàn)求分式的值的幾種方法.
1 參數(shù)法
參數(shù)法是解決求分式的值這類問題時最常用的方法,掌握這種方法,也就能解決大部分求分式的值的問題[1].

分析:這道題中的條件以等比的形式出現(xiàn),那么可以假設(shè)該比的比值為k,把待求式轉(zhuǎn)化為關(guān)于k的代數(shù)式的值.

x=3k,y=4k,z=6k.
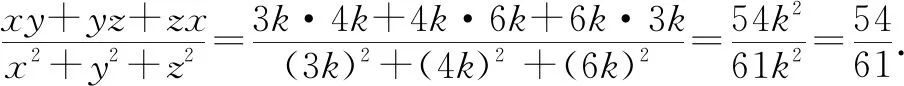
方法總結(jié):參數(shù)法指的是在解題過程中,通過適當引入一些與題目研究的數(shù)學對象發(fā)生聯(lián)系的新變量(參數(shù)),以此作為媒介,再進行分析和綜合,從而解決問題[2].此外,運用參數(shù)法需注意兩個問題:
第一,所設(shè)參數(shù)應(yīng)保證不為零;
第二,不要受到引入的參數(shù)的干擾,因為最終該參數(shù)會消去.
在例1中,通過引入?yún)?shù)k,將x,y,z均用含k的代數(shù)式表示出來,最后消去參數(shù)k,求得結(jié)果.
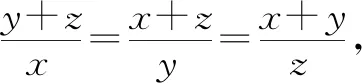

y+z=kx,
①
x+z=ky,
②
x+y=kz.
③
于是,由①+②+③,可得
y+z+x+z+x+y=kx+ky+kz,
2(x+y+z)=k(x+y+z).
因為x+y+z≠0,所以k=2.

2 兩頭湊法
所謂兩頭湊法,其實就是觀察條件的特點思考所求分式需要怎樣的信息,或觀察所求分式的特點思考需要怎樣的條件[3].

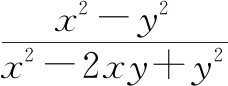
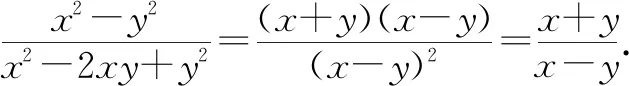
④

將x=3y代入④,得
解法2:由于xy≠0,則根據(jù)分式的基本性質(zhì),將分式的分子、分母同時除以xy,得

所以,由⑤得
方法總結(jié):解決分式的求值問題,最有效的方法是將題目已知條件和所求問題一同考慮.根據(jù)這一思路,首先要考慮條件能為所求問題提供什么有價值的信息,然后考慮所求問題需要條件能提供什么有效信息,這就是兩頭湊法[4].
需注意的是,在變形已知條件時,應(yīng)該使變形所得到的式子在所求的式子中可用,如解法1;或者,變形所求的式子時,應(yīng)該與已知條件有明顯的、直接的聯(lián)系,如解法2.
3 整體法
整體法和“認識分式”這一章中蘊含的整體思想有關(guān)聯(lián).
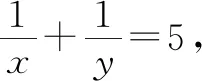

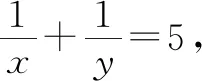
x+y=5xy.
⑥

所以將⑥代入⑦中,得
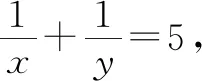



解法3:由題意可知x≠0,y≠0,所以xy≠0.
將分式的分子、分母同時除以xy,可得
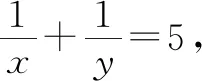

總而言之,求分式的值的方法非常多.本文中所例舉的參數(shù)法、兩頭湊法和整體法是幾種比較常用的方法.這幾種方法靈活性較強,一線數(shù)學教師應(yīng)抓住機會構(gòu)建高效課堂,讓學生在這樣的課堂中得到較充分的訓練.

