畸形波在有限水深中的演化和時頻能量研究

羅春蓮

（廈門海洋職業技術學院航海學院，福建 廈門 361012）

畸形波是一種具有大波高、能量高度集中的波浪[1]。發生時將嚴重破壞海洋結構物，嚴重威脅著人們的生命安全。科學家們開始致力于對畸形波的研究，并取得了豐碩的成果。Mori等人[2]基于YURA港的波浪數據，分析得到畸形波波高與有義波高的最大比值約為2.6；Sand 等人[3]基于北海的波浪數據，分析得到畸形波波高與有效波高的最大比值約為2.9。

現階段有關有限水深和深水畸形波的規律研究多從B-F 不穩定性出發。Whitham[4]基于B-F 不穩定性推導了守恒型方程，Chu 等人[5]修正了Whitham 方程。Osborne 等人[6]基于三階非線薛定諤方程研究畸形波，結果表明畸形波是以B-F 不穩定性模式存在的。張運秋[7]改用4 階NLS 方程，并基于偽譜法，對畸形波進行數值模擬，模擬了更大波陡的畸形波。

上述研究表明，三階性薛定諤可較好地描述畸形波的演化過程。為更簡便地對非線性方程進行研究，避免使用理論方法研究非線性方程的困難性[8]。本文主要通過數值求解NLS 方程，探討了畸形波生成前后的演化過程，揭示了畸形波的演化規律及頻率規律。

1 NLS 方程

作為本文研究的理論背景，對三階非線性薛定諤方程的推導作闡述[9]。連續性條件：

動力學邊界條件：

運動學邊界條件：

水底邊界條件：

有限水深條件，式（4）轉化為以下形式：

方程（4）和（5）依據泰勒級數展開，展開到三階。

引入尺度變量：

φ和η以ε的展開為：

多尺度展開如下：

將式（9）、（10）和（11）代入式（1）、（2）、（3）和（4）中，推導得式（12）和（13）。

其中，∣A∣為復波包，φ10為平均流勢。

當?/?y1=0 時，可得如下三階非線性薛定諤方程（NLSE）：

本文采用偽譜方法求解NLS 方程，其中，偽譜法隱含了周期為2π的空域，周期性條件如下：

A(t,x)的傅里葉變換及逆變換（0＜t＜2π）如下所示：

2 呼吸子解畸形波演化的數值模擬

基于呼吸子解畸形波[1（0]式24），對NLSE數值求解，研究畸形波在有限水深的演化過程。

其中，td表示無因次時間。

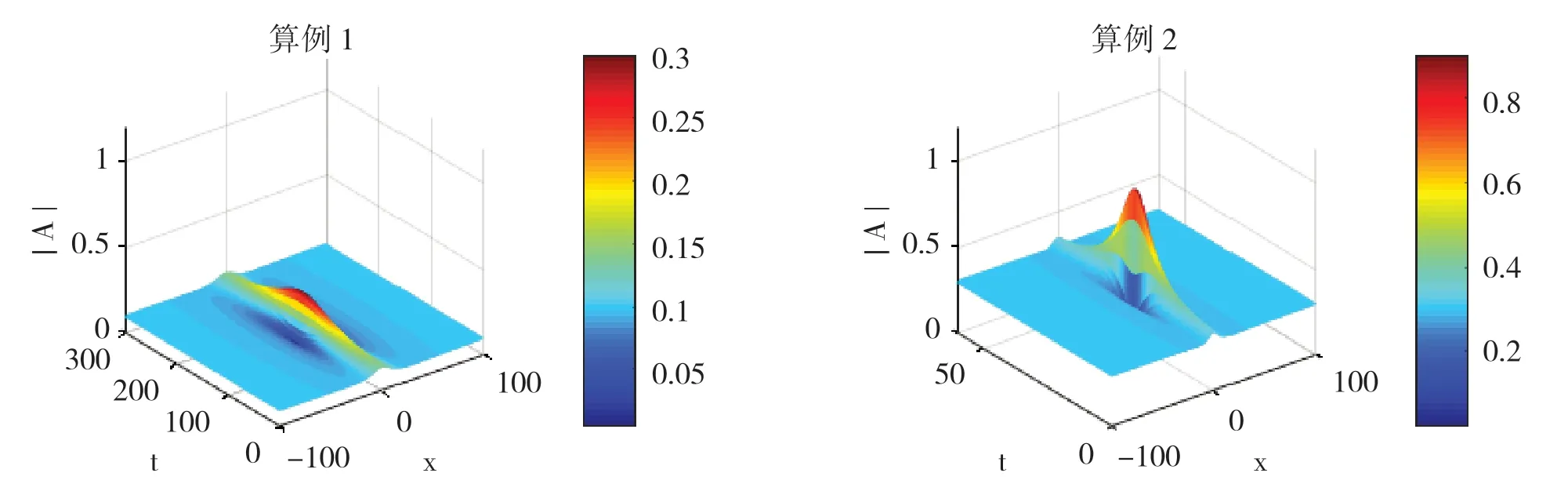
圖1 畸形波的復波包絕對值

圖1 給出了2 種算例下畸形波復波包絕對值在不同時刻的演化過程。研究表明：在有限水深下，畸形波生成時，波高瞬間增大；畸形波消失時，波高瞬間減小，生成和消失具有快速性；算例1中，初始波幅為0.1時，最大波幅約為0.3，算例2 中，初始波幅為0.3 時，最大波高約為0.9，2 個算例皆表面畸形波生成時刻，最大波幅約為平均波幅的3 倍，這也與其他學者研究的相對應。

3 畸形波的時頻能量研究

基于上述2 種算例的數值模擬，結合小波變化，進一步研究畸形波從生成到消失過程中，開始位置（x1=-100），聚焦位置（x2=0），消散位置（x3=100）的能量和頻率變化。

算例1 與算例2 的能量特征分析表明：畸形波生成前（x1=-100），能量較小，畸形波生成處（x2=0），能量增大，畸形波消失處（x3=100），能量減小；算例2 的初始波幅是算例1 的3 倍，而算例2 譜峰度最大值是算例1 的7 倍，這表明初始波幅越大，畸形波生成時的能量越大。

同時，算例1 與算例2 的時頻特征分析表明：畸形波生成前（x1=-100）、畸形波生成處（x2=0）和畸形波消失處（x3=100），波浪能量始終集中在f=0.5Hz 處，頻率無變化。

4 結語

1.本文基于偽譜法，通過傅里葉變換和逆變換，將非線性NLS 方程簡化為離散化的常微分方程組，實現方程的求解，并進一步研究呼吸子解畸形波在有限水深中的演化規律和時頻能量特征。

2.研究表明：在有限水深下，畸形波生成時，波高瞬間增大；畸形波消失時，波高瞬間減小，生成和消失具有快速性；畸形波生成時刻，最大波幅約為平均波幅的3 倍，時頻能量譜顯示能量集中程度隨波高的增大而增大，畸形波消失時，能量集中程度隨波高的減小而減小，但波浪能量始終集中在f=0.5Hz 處，頻率無變化。