貝葉斯網絡變量消元法最優消元順序構造

任東平 郭建喜 郝小禮 蔣濤

1.海軍勤務學院基礎部；2.海軍裝備部裝備保障大隊

變量消元法（Variable Elimination， VE）是貝葉斯網絡眾多推理算法中最基本的一個，其推理的快慢和復雜度主要取決于消元的順序。尋找最優消元順序是一個非確定性多項式難解算法（Nondeterminism Polynomial Hard， NP-Hard）問題，在實際中常采用啟發式搜索來求解。為了提高變量消元法的推理速度，在此對最小度、最大勢、最小缺邊和最小增加復雜度搜索方法進行了研究，以亞洲網絡為例，分析計算了上述搜索方法的復雜度和消元順序，通過MATLAB R2018a對上述不同搜索方法分別進行網絡構建和推理，最后通過推理時間分析比較了4種搜索方法的性能。實驗結果表明最小增加復雜度搜索方法優于其他搜索方法，其平均耗時最少為0.012s，可加快貝葉斯網絡的推理過程。

貝葉斯網絡源于Pearl[1]提出的不確定知識表示模型，因其有著概率論的嚴謹理論基礎，以圖模型清晰地表示隨機事件之間的相互依賴關系，成為人工智能、模式識別和故障診斷等領域的研究熱點[2]。貝葉斯網絡推理主要有兩種方法：精確推理和近似推理。精確推理主要有變量消元法（Variable Elimination）、團樹傳播算法（Clique Tree Propagation）、多樹傳播（Polytree Propagation）和圖約簡算法（Graph Reduction）等。其中，變量消元法是最基本的推理算法，也較容易理解，其優勢在于它的通用性和簡易性，能夠很好地解決復雜貝葉斯網絡的推理，尤其是復雜的故障診斷貝葉斯網。

變量消元法的復雜性主要取決于其消元的先后順序，尋找最優消元順序是一個NP-難解問題[3]，目前普遍采用近似算法求解，主要有最小度搜索[4]、最大勢搜索[2，5]、最小缺邊搜索[2]，向光軍通過對變量消元法的分析，提出了最小缺邊搜索（Minimum Deficiency Search， MDS）和變量消元并行運行的算法[6]，但該算法沒有找到最優的消元順序，仍存在一定的缺陷；高文宇提出了一種新的搜索算法——最小增加復雜度搜索[7]，但只是通過仿真實驗進行說明，而沒有用到實例中，未給出其搜索方法的具體實現過程，也沒有和上述搜索方法進行對比。針對以上問題，本文以貝葉斯網絡經典模型亞洲網絡來驗證上述搜索算法在變量消元法中的優劣。

1 貝葉斯網絡

貝葉斯網絡（Bayesian Network）是一個有向無環圖，其中的節點表示事件中的隨機變量，有向邊則表示節點之間的相互依賴關系。每個節點都有概率分布，根節點的概率分布屬于邊緣分布，也可稱為先驗概率；非根節點則是條件概率。

在概率論中，可以用條件概率鏈[8]的形式表示其聯合概率，其形式如式（1）所示：

公式（1）也可以稱為鏈規則，其中Y為隨機變量，P（Y1,Y2,… ,Yk）是Y1,Y2,… ,Yk的聯合 概率，P（Yi|Yi-1, … ,Y1）是Yi,Yi-1, … ,Y1的條件概率。

將貝葉斯網絡條件獨立性假設用于鏈規則公式（1）可得到如式（2）所示：

其中P（Yi|Parent（Yi））為貝葉斯網絡節點Yi的條件概率，Parent（Yi）表示Yi的直連父節點。

為了下文論述，在這里引入貝葉斯網絡的一個經典模型——亞洲網絡[9]。抽煙可能會引起肺癌或者支氣管炎，出訪亞洲可能會導致肺結核，這3種疾病的任何一種都有可能會導致呼吸困難。若有肺結核或者肺癌，X光胸透結果可能呈陽性，把這些因果關系結合起來，便得出了經典的亞洲網絡模型，如圖1所示，其中V表示到過亞洲，T表示感染肺結核，S表示抽煙，L表示患有肺癌，B表示患有支氣管炎，E表示感染肺結核或者患有肺癌，X表示拍攝X光，D表示呼吸困難。用公式（2）表達如圖1所示中的各個節點的聯合概率分布可得到如式（3）所示：

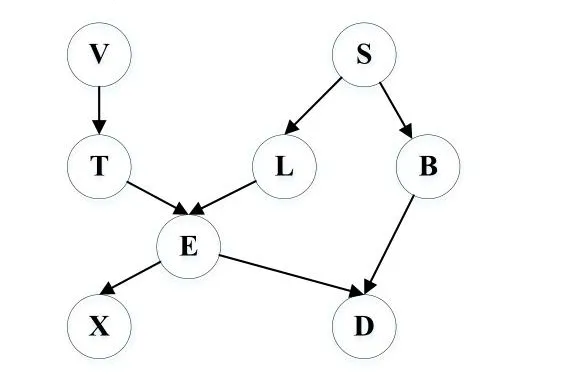
圖1 亞洲網絡模型Fig.1 Asian network model

如表1所示為亞洲網絡節點概率，其中P（i）表示節點i的先驗概率，P（i|j）表示在j為真時節點i的條件概率，）表示在j為假時節點i的條件概率。

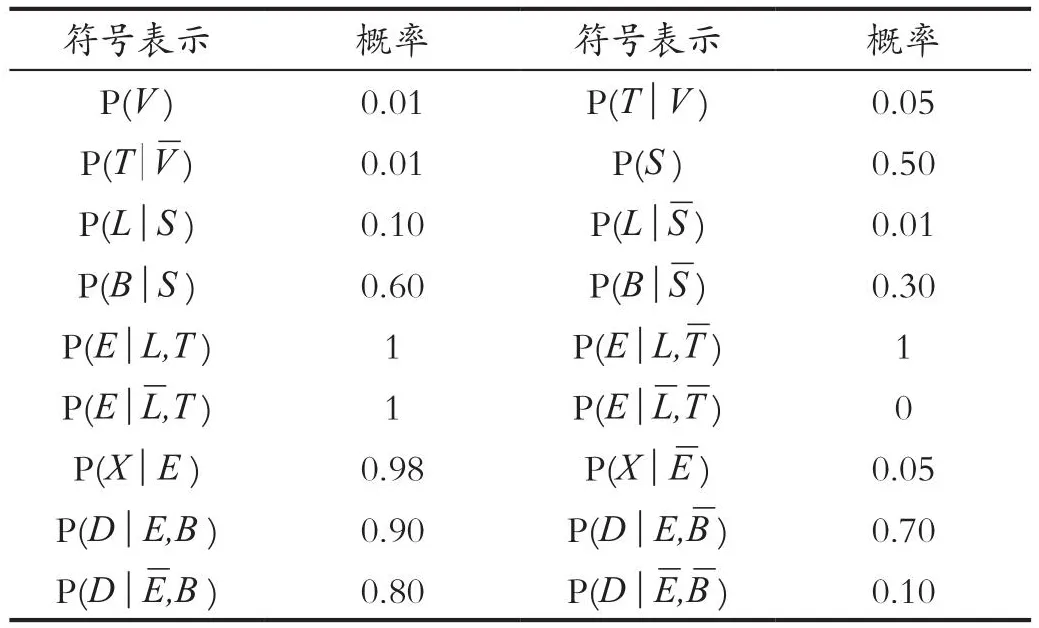
表1 亞洲網絡節點概率Tab.1 Probability of asian network nodes

2 變量消元法

假設F是關于變量集X={X1，X2，…，Xn}的一個函數，而f={f1，f2，…，fm}也是一組函數，其中f所涉及的變量都是變量集X的一個子集。如果則f為F的一個分解，f1，f2，…，fm稱為F的分解因子。消元方式可以分為兩種。一種是從F={X1，X2，…，Xn}出發，通過的方式完成X1的消元；另一種從f={f1，f2，…，fm}出發，將與X1的所有相關函數{f1，f2，…，fk}，利用公式行消元，并將返回到f中，就實現了X1的消元。

通過以上敘述，若采用第一種消元方式，其計算的復雜度相對于變量的個數n成指數增長；若采用第二種消元方法，其計算的復雜度僅僅依賴于涉及X1的分解因子f1,f2,… ,fk的變量數量，其計算復雜度會大大減小。

假設用X來表示一個貝葉斯網絡N中所有變量節點的集合，用f表示N中所有節點概率分布的集合，依據貝葉斯網絡的定義，則f可視為N表示的聯合概率分布P(X)的一個分解。假設觀測到了證據集E={E1,E2, …,Em}，它們的取值記為e。在集合f的因子中，將所有表示證據的變量設置為實際觀測值，就可以得到另一組函數，記之為f ′。這一步驟稱為設置證據，f ′是函數P(Y，E=e)的一個分解，這里Y=X∩。

設Y的一個子集為Q，f ′從中依次消去所有在Y中，但不在Q中的變量，就可以得到另一個函數集合，記為f ′′。f ′′是P(Q，E=e)的一個分解，將f ′′中的所有因子相乘便得到P(Q，E=e)。按照條件概率的定義可得到如式(4)所示：

VE算法需要提供5個輸入量：（1）貝葉斯網絡N，同時也是聯合分布P（X）的一個分解；（2）證據變量的集合E；（3）證據變量集合E的取值e；（4）查詢變量的集合Q；（5）所有不在Q∪E中的變量的排序ρ，即為消元的順序。對于聯合分布P（X）的獲取采用公式（2），只需按照網絡拓撲圖寫出聯合分布即可；證據集變量集合E以及E的取值e均由人員觀測得到；查詢變量Q即為所求事件；消元順序ρ的獲取需要通過搜索方法來獲取，不同的搜索方法獲取不同的消元順序，以上即為變量消元法的輸入量。VE推理算法的代碼實現如表2所示。

表2 VE算法的實現過程Tab.2 Implementation process of VE algorithm

3 消元復雜度分析

從變量消元法的實現過程可以看出，最耗費時間和內存的步驟是對Elim(f，Z)這一函數的調用。這一函數的運算量遠超其他步驟的運算，所以說整個變量消元法的計算復雜度主要是由這一函數來決定的。

函數Elim(f，Z)表示從f中挑出所有包含Z的函數{f1，…，fk}，將它們相乘，得到中間函數G，再從G中消去Z。設X1，…，Xk是G中所有除Z之外的變量，如果把函數表示成多維表，則G所需存儲的函數個數為綜上所述，是函數G復雜性的一個度量，從而也是Elim(f，Z)復雜性的一個度量，稱之為變量Z的消元成本，記為δ(Z)[2，6]，如式（5）所示。

用變量消元法進行推理時，需要消去多個變量，設它們依次為Z1, Z2, …,Zn。在這里用總消元成本來衡量變量消元法的總復雜度。以亞洲網絡為例，函數集合為f={P（V） ,P（S）,P（T|V） ,P（L|S）,P（B|S）,P（D|B,E）,P（X|E）,P（E|T,L）}。設證據節點為X=1，E=1，計算V的可信度，即求P(V|X=1，E=1)的概率，消元順序為ρ=＜D,B,L,S,T＞，網絡中所有變量均取二值。消去D時，需要計算G=P(D|B，E)，共涉及3個變量：D、B、E，所以D的消元成本δ(D)=2×2×2=8。依次類推，其余4個節點B，L，S，T的消元成本分別為 4，8，2，4。則按此消元順序進行消元的總成本為26。

所謂結構圖就是考慮一個函數的集合F={f1，…，fm}，F的結構圖可定義為從一個空圖出發，對F中的每一個變量，在圖中相應的添加一個節點，對于任意兩個變量X和Y，如果它們同時出現在同一個因子fi中，則在它們對應的節點之間添加一條邊。按此規則構建的圖模型為結構圖。如圖2所示為亞洲網絡結構圖。

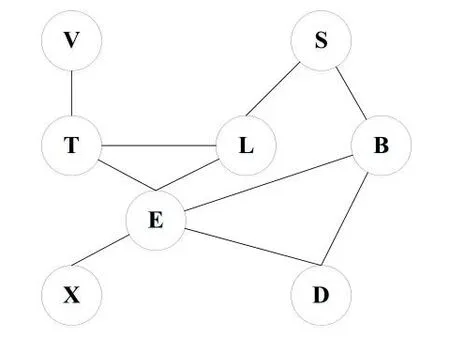
圖2 亞洲網絡結構圖Fig.2 Asia network structure diagra m

從一組函數f中消去一個變量Z的成本，能從該函數的結構圖中算得。如前所述，從f中消去Z的成本其中X1，…，Xl是除Z之外的變量，Z是函數所涉及到的所有變量，f1，…，fk是所有涉及Z的因子。根據上文對結構圖的定義，在f的結構圖中，{X1，…，Xl}剛好是所有與Z相鄰節點的集合，記為nb(Z)，因此有如式（6）所示：

在亞洲網絡中，從f中消去變量T需要計算G=P(T|V)P(E|T，L)，涉及到4個節點{T，V，E，L}，所以在結構圖中，與T相鄰的節點使nb（T） ={V,L,E}，所以δ(T)也可以按公式（5）計算，即

4 消元順序構造

4.1 最小度法

在結構圖中，最小度搜索法就是把度數最小的節點變量放到消元順序隊列的末尾，并在網絡中刪去該節點和連接該節點的有向邊。若有多個節點的度數相同，則任選其一，重復上述過程，直到消去結構圖中所有的節點。此消元法稱為最小度方法。以亞洲網絡模型為例，設證據節點為X=1，E=1，其中1表示事件為真。分別求V，T，S，L，B，D的后驗概率。即求P(V|X=1，E=1)，P(T|X=1，E=1)，P(S|X=1，E=1)，P(L|X=1，E=1)，P(B|X=1，E=1)，P(D|X=1，E=1)的概率。采用最小度搜索方法求消元順序，總消元順序為ρ=＜E,D,B,L,S,T,X,V＞。求節點V時的消元順序為ρ=＜D,B,L,S,T＞，由第二節中的公式（3）可得其聯合分布為如式（7）所示：

消去元素D如式（8）所示：

消去元素B如式（9）所示：

消去元素L如式（10）所示：

消去元素S如式（11）所示：

消去元素T如式（12）所示：

計算V的后驗概率分布得到如式（13）所示：

計算V的最大假設檢驗得到如式（14）所示：

上述過程即為變量消元法的推理計算過程，在MATLAB R2018a中構建亞洲網絡，求得P （V= 1 |X= 1 ,E= 1 ） =0.01，

耗時0.0750s（后續不同搜索方法的推理計算過程均如上，不再贅述）。同樣求T時的消元順序為ρ=＜ D,B,L,S,V ＞；求S時的消元順序為ρ=＜ D,B,L,T,V ＞；求L時的消元順序為ρ=＜ D,B,S,T,V ＞；求B時的消元順序為ρ=＜ D,L,S,T,V ＞ ；求 D 時的消元順序為ρ=＜ B,L,S,T,V ＞。可得各個節點的推理時間分別為0.0239s，0.0127s，0.0164s，0.0146s，0.0264s。其平均推理耗時為0.0282s。

4.2 最大勢搜索

最大勢搜索是根據以下規則在無向圖中對所有節點進行編號：在有n個節點的無向圖中，在第i步中，選擇擁有最多已編號的相鄰節點，且這些節點未編號，將其編號為n-i+1。如果存在多個這樣的節點，則任選其一。當無向圖中所有節點都被編完號后，將編號按照由小到大的順序排序，其順序就是對應節點的消元順序，此為最大勢搜索方法的一般思想。運用最大勢搜索方法求亞洲網絡消元順序：第1步先對B節點編號為8，第2步可對節點S或者D編號，這里將D節點編號為7，第3步對節點S編號為6，第4步對節點L編號為5，第5步對E節點編號為4，第6步可對節點T或者X編號，這里選擇將T編號為3，第7步將節點V編號為2，第8步將最后一個節點X編號為1。至此所有節點均已編號，其消元順序為ρ=＜ X，V，T，E，L，S，D，B ＞。除去證據節點X和E，可的相應節點的消元順序，求V時的消元順序為ρ=＜ T，L，S，D，B ＞；求T時的消元順序為ρ=＜ V，L，S，D，B ＞；求S時的消元順序為ρ=＜ V，T，L，D，B ＞；求L時的消元順序為ρ=＜ V，T，S，D，B ＞；求B時的消元順序為ρ=＜ V，T，L，S，D ＞；求 D 時的消元順序為ρ=＜ V，T，L，S，B ＞。可得各個節點的推理時間分別為0.0258s，0.0126s，0.0118s，0.0126s，0.0118s，0.0146s。其平均推理耗時為0.0149s。

4.3 最小缺邊搜索

無向圖中某個節點Z的缺邊數就是在用函數Elim(f，Z)消去Z時需要添加的邊數。最小缺邊搜索一邊計算節點的缺邊數，一邊將節點從無向圖中刪除。每一步都需計算節點的缺邊數，在消去節點時選擇缺邊數最小的節點進行刪除，當同時有多個節點的缺邊數相同時，任選其一，如此循環，直到所有節點均被刪除。仍以亞洲網絡模型為例，在初始時，節點{V，S，T，L，B，E，X，D}的缺邊數分別為 {0，1，2，2，2，8，0，0}，任選其一，這里選擇 V。消去 V后節點{S，T，L，B，E，X，D}的缺邊數分別為 {1，0，2，2，8，0，0}，任選其一，這里選擇X。消去X后節點{S，T，L，B，E，D}的缺邊數分別為{1，0，2，2，6，0}，任選其一，這里選擇T。消去T后節點{S，L，B，E，D}的缺邊數分別為{1，1，3，3，0}，消去D。消去D后節點{S，L，B，E}的缺邊數分別為{1，1，1，1}，由于節點S，L，B，E構成一個環，所以缺邊數相同，可消去任意一個，這里選擇消去E，其余3個節點可任意消去，這里選擇的順序為L，S，B。綜上所述，最小缺邊搜索法的消元順序為ρ=＜V，X，T，D，E，L，S，B ＞。除去證據節點X和E，可得其他節點的消元順序，求V時的消元順序為ρ=＜ T，D，L，S，B ＞；求T時的消元順序為ρ=＜ V，D，L，S，B ＞；求 S 時的消元順序為ρ=＜ V，T，D，L，B ＞；求L時的消元順序為ρ=＜V，T，D，S，B ＞；求B 時的消元順序為ρ=＜ V，T，D，L，S ＞；求D時的消元順序為ρ=＜ V，T，L，S，B ＞。可得各個節點的推理時間分別為 0.0150s，0.0122s，0.0119s，0.0119s，0.0121s，0.0125s。其平均推理耗時為0.0126s。

4.4 最小增加復雜度搜索

其主要思想是在結構圖中消元時，刪除某個節點，與該節點相連的所有邊均會被刪除，為了降低圖的復雜度，往往是希望刪除的越多越好，在這里將刪去邊的條數用ed表示；當節點刪除后，需要將刪除后的圖構成一個完備圖，所以會在某些節點之間添加一些邊，使其構成完備圖，但添加的邊又會增加圖的復雜度，所以希望添加的邊越少越好，將添加的邊數記為ea，用ea/ed可得一個新的衡量指標，即最小增加復雜度，用IC表示。選擇消元順序時，先計算出所有節點的IC值，選擇IC值最小的進行消元，若有多個相同值，則任選其一，接著計算余下節點的IC值，如此重復，直到所有節點被消去，可得出消元順序。最小增加復雜度搜索方法是一個動態的搜索過程，從整個網絡圖出發，對其不斷地循環判斷，以尋得最優解，提高推理整體的運行時間，避免了局部消元過快而整體較慢的不足。此算法適用于故障診斷時對多查詢變量的消元，能夠提高整體的運行時間。以亞洲網絡為例，運用最小增加復雜度搜索方法，如表3所示為初始狀態節點的IC值。

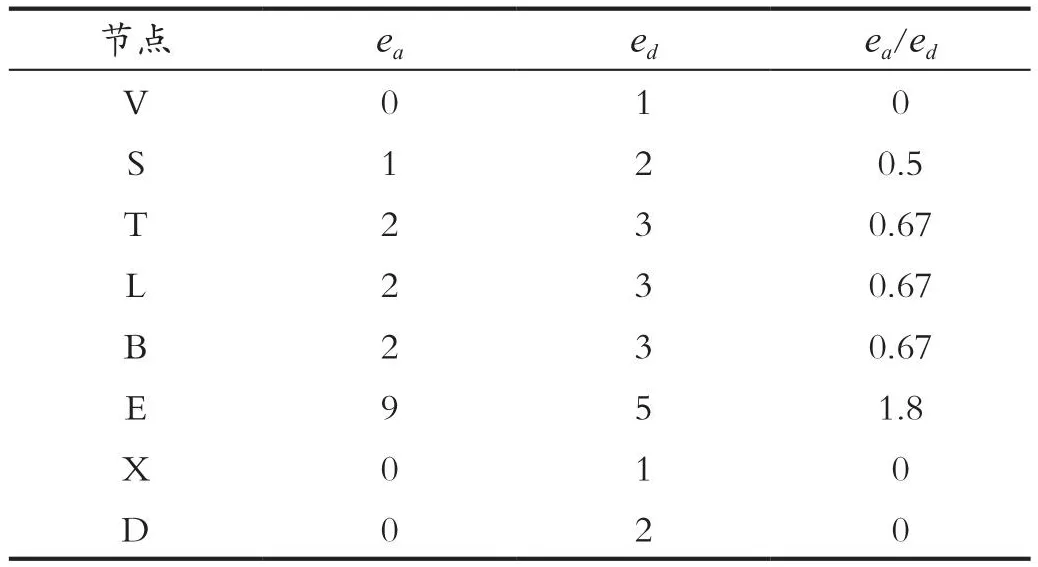
表3 初始狀態節點IC值Tab.3 Initial state node IC value

由表3可知，節點V，X，D的IC值均為0，可任選其一進行消元，這里選擇節點V，消去節點V后可得其余節點的IC值，如表4所示。

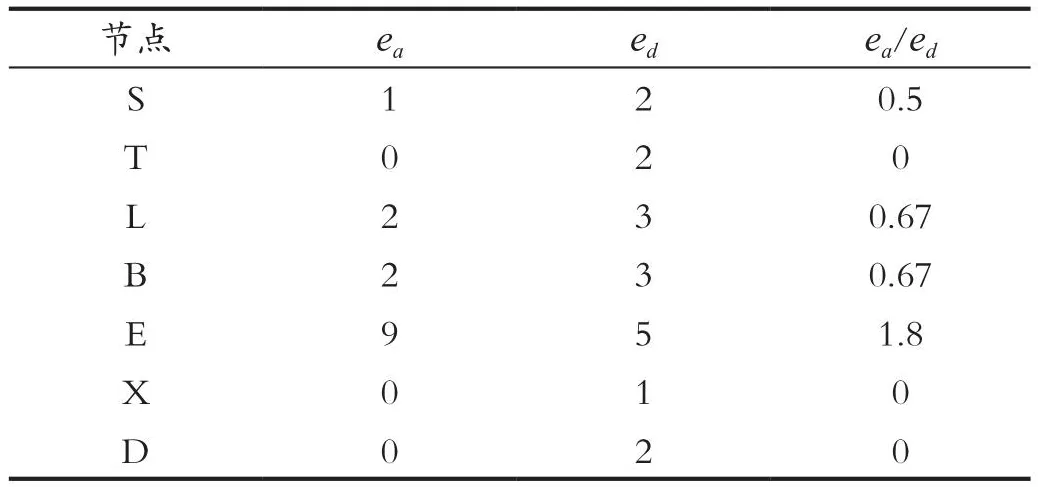
表4 消去節點V后節點IC值Tab.4 Node IC value after eliminating node V

由表4可知，節點T，X，D的IC值均為0，可任選其一進行消元，這里選擇節點D，消去節點D后可得其余節點的IC值，如表5所示。

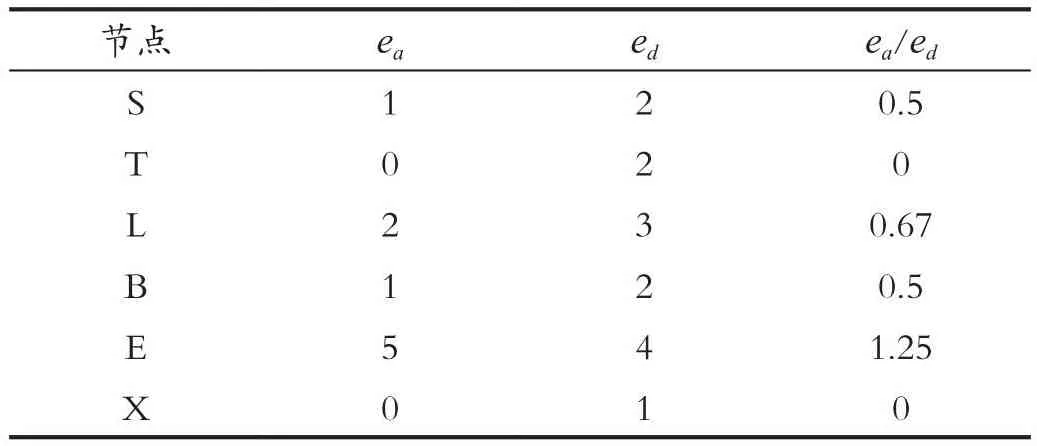
表5 消去節點D后節點IC值Tab.5 Node IC value after eliminating node D

由表5可知，節點T，X的IC值均為0，可任選其一進行消元，這里選擇節點X，消去節點X后可得其余節點的IC值，如表6所示。

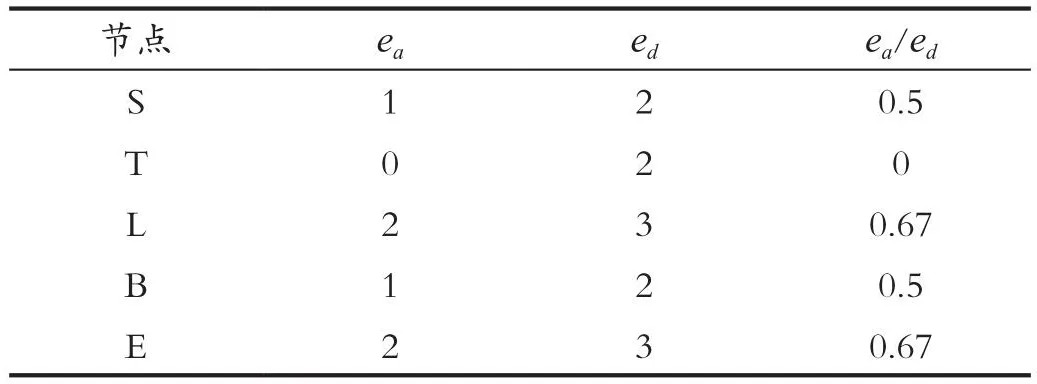
表6 消去節點X后節點IC值Tab.6 Node IC value after eliminating node X

由表6可知，節點T的IC值均為0，消去節點T后可得其余節點的IC值，如表7所示。

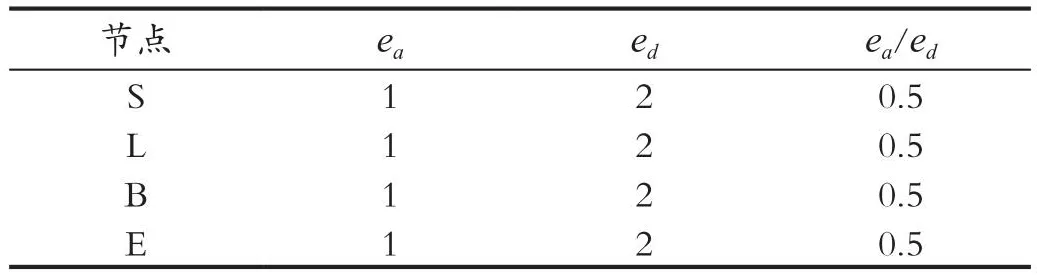
表7 消去節點T后節點IC值Tab.7 Node IC value after eliminating node T

由表7可知，節點S，L，B，E的IC值均為0.5，可任選其一進行消元，這里選擇節點S，消去節點S后余下的節點L，B，E構成一個三角圖，所有節點都是等效的，可任意組合。最終得出消元順序ρ=＜ V，D，X，T，X，L，B，E ＞。可得各個節點的推理時間分別為0.0119s，0.0130s，0.0124s，0.0116s，0.0115s，0.0116s。其平均推理耗時為0.012s。如圖3所示為4種推理算法平均耗時對比，可以明顯的看出最小增加復雜度搜索算法運行時間優于其他3種搜索方法。

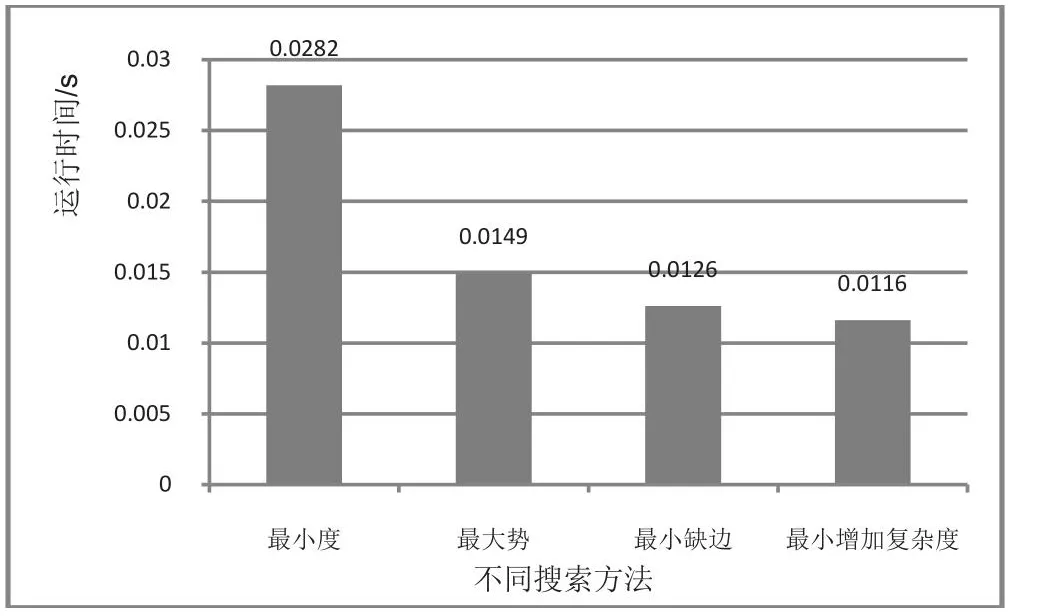
圖3 不同推理算法對比Fig.3 Comparison of different inference algorithms

5 結語

貝葉斯網絡有著廣泛的應用前景，可用于人工智能、故障診斷等領域，計算速度的快慢直接決定著該方法在上述領域能否較好的應用。故本文以亞洲網絡模型為例，在推理實例中論述了變量消元法的實現過程，通過MATLAB R2018a對亞洲網絡進行構造和推理，通過實驗分別對比了變量消元法的4種消元順序構造法，實驗表明最小增加復雜度搜索算法優于其他搜索算法，可有效減少推理運算的時間。

引用

[1]PEARL J.Fusion,Propagation,and Structuring in Belief Networks[J].Artificial Intelligence,1986(3):241-288.

[2]張連文.貝葉斯網引論[M].北京:科學出版社,2006.

[3]COOPER G F.The Computational Complexity of Probabilistic Inference Using Bayesian Belief Networks[J].Artificial Intelligence,1990,42(2):393-405.

[4]AMESTOY P R,DAVIS T A,DUFF I S.Algorithm 837:AMD,an Approximate Minimum Degree Ordering Algorithm[J].ACM Transactions on Mathematical Software,2004,30(3):381-388.

[5]BERRY A,BLAIR J R S,HEGGERNES P,et al.Maximum Cardinality Search for Computing Minimal Triangulations of Graphs[J].Algorithmica (New York),2004,39(4):287-298.

[6]向光軍,孔兵,歐家欽.貝葉斯網絡VE推理算法的并行化研究[J].云南大學學報(自然科學版),2010,32(4):392-395.

[7]高文宇,張力.貝葉斯網最優消元順序的近似構造算法[J].計算機應用,2011,31(8):2072-2074.

[8]李儉川.貝葉斯網絡故障診斷與維修決策方法及應用研究[D].長沙:中國人民解放軍國防科學技術大學,2002.

[9]ZHANG N L.Hierarchical Latent Class Models for Cluster Analysis[C]//National Conference on Artificial Intelligence,2002:230-237.

[10][ZHANG N L,POOLE D.Exploiting Causal Independence in Bayesian Network Inference[J].The Journal of Artificial Intelligence Research,1996.