立體幾何中平行與垂直問題的解題策略
■陜西省禮泉縣第一中學 張西情
平行和垂直這兩種位置關系的證明是立體幾何中的重點和難點,也是永恒不變的主題。主要考查同學們的空間想象能力、邏輯推理能力,以及數學抽象、邏輯推理和直觀想象等數學學科素養。本文主要針對解答題中位置關系的證明與探索展開,希望能給同學們的高考備考提供一些幫助。
一、平行關系的證明
例1如圖1,在四棱 錐P-ABCD中,PA⊥平面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M為線段AD上一點,AM=2MD,N為PC的中點。
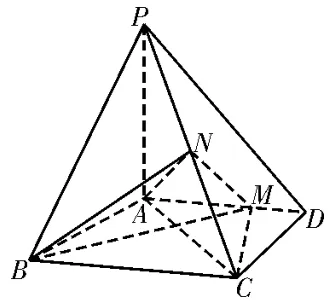
圖1
(1)證明:MN∥平面PAB;
(2)求直線AN與平面PMN所成角的正弦值。
解析:(1)法一(線面平行的判定定理):取PB的中點Q,連接AQ,NQ,如圖2,因為N是PC的中點,所以NQ∥BC,且NQ=BC。又因為AM=BC=BC,且AM∥BC,所以QN∥AM,且QN=AM,所以四邊形AQNM是平行四邊形。所以MN∥AQ。又MN?平面PAB,AQ?平面PAB,所以MN∥平面PAB。

圖2
法二(面面平行的性質定理):取BC的中點E,連接EM,EN,如圖3,因為N是PC的中點,所以EN∥PB。又EN?平面PAB,所 以EN∥平 面PAB。因為BE=BC=2,AM=2MD=AD=2,且AD∥BC,所以四邊形ABEM為平行四邊形,所以EM∥AB。又EM?平面PAB,所以EM∥平面PAB。又EM∩EN=E,所以平面EMN∥平面PAB,所以MN∥平面PAB。

圖3
(2)取BC的中點E,連接AE。由AB=AC得AE⊥BC,從而AE⊥AD,且AE=
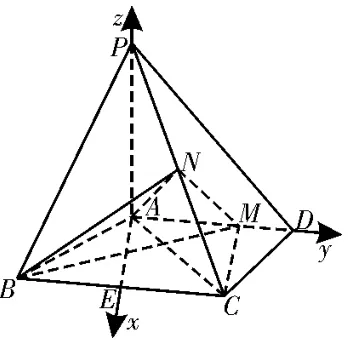
圖4
點撥:證明線面平行的位置關系的常用方法有:①利用線面平行的判定定理證明;②利用面面平行的性質定理證明;③利用空間向量證明。平行問題主要是線線平行、線面平行和面面平行。一般來說,三者之間是可以利用判定定理和性質定理相互推出。問題的核心是線線平行,而證明線線平行的方法有:①平行公理;②中位線;③平行四邊形;④線面平行的性質定理;⑤線面垂直的性質定理等。
二、垂直關系的證明
例2如圖5,在四棱錐P-ABCD中,底面ABCD為正方形,平面PCD⊥平 面ABCD,且PC=PD=,CD=2。
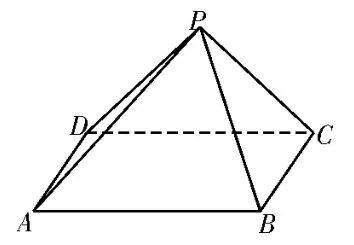
圖5
(1)證明:PC⊥平面PAD;
(2)求點D到平面PAB的距離。
解析:(1)法一(線面垂直的判定定理):因為平面PCD⊥平面ABCD,平面PCD∩平面ABCD=CD,AD⊥CD,AD?平面ABCD,所 以AD⊥平 面PCD。又PC?平面PCD,所以AD⊥PC。在△PCD中,PC=PD=,CD=2,PC2+PD2=CD2,所以PC⊥PD。因為PD∩AD=D,PD,AD?平面PAD,所以PC⊥平面PAD。

圖6

圖7
點撥:證明直線和平面垂直的常用方法:①判定定理;②垂直于平面的傳遞性(a∥b,a⊥α?b⊥α);③面面平行的性質(a⊥α,α∥β?a⊥β);④面面垂直的性質;⑤向量法。垂直問題主要是線線垂直、線面垂直和面面垂直。三者可以通過判定定理和性質定理互相轉化,問題的核心是線線垂直,而證明線線垂直的方法有:①勾股定理逆定理;②等腰三角形三線合一;③菱形對角線相互垂直;④直徑所對的圓周角為;⑤線面垂直的性質等。
三、平行、垂直關系中的探索性問題
處理空間中平行或垂直的探究性問題,一般根據條件先猜測點的位置,再給出證明。從近幾年高考命題看,考查力度與以往基本相同,與之相關的題目,難度較大。
1.平行關系中的探索性問題
例3如圖8,在三棱錐A-BCD中,平面ABD⊥平面BCD,E,F分別是BD,AC的中點,且AB=BE=AE=CE,BC=DC。
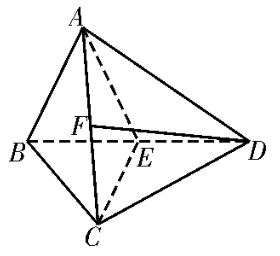
圖8
(1)在線段AB上是否存在點G,使得DF∥平面CEG? 若存在,求出的值;若不存在,請說明理由。
(2)求直線DF與平面ACE所成角的正弦值。
解析:(1)假設在線段AB上存在點G,使得DF∥平面CEG。
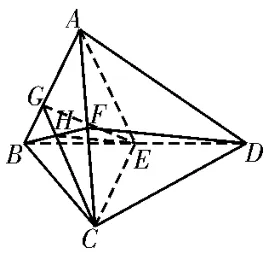
圖9
因為CE⊥平面ABD,所以平面ACE⊥平面ABD,過點D作DM⊥AE交延長線于點M,如圖10,DM⊥CE,CE∩AE=E,則DM⊥平 面ACE,連接FM,則∠DFM即為直線DF與平面ACE所成的角。

圖10
點撥:假設結論成立,在△BDF中,作出EH∥DF,延長CH找到點G,設參數λ,利用向量三點共線定理求出參數,確定點G并求出比值。
2.垂直關系中的探索性問題
例4如圖11,在四棱錐P-ABCD中,PA⊥底面ABCD,底面ABCD為直角 梯 形,AB∥CD,AB⊥AD,且CD=2AB。

圖11
(1)若AB=AD,直線PB與CD所成的角為45°,求二面角P-CD-B的大小;
(2)若E為線段PC上一點,試確定點E的位置,使得平面EBD⊥平面ABCD,并說明理由。
解析:(1)因為AB⊥AD,CD∥AB,所以CD⊥AD。因為PA⊥平面ABCD,CD?平面ABCD,所以PA⊥CD。又PA∩AD=A,所以CD⊥平面PAD。又PD?平面PAD,所以CD⊥PD,所以∠PDA是二面角P-CD-B的平面角。又直線PB與CD所成的角為45°,所以∠PBA=45°,即PA=AB。在Rt△PAD中,PA=AD,有∠PDA=45°,即二面角P-CD-B的大小為45°。
(2)當點E在線段PC上,且滿足PE∶EC=1∶2時,平面EBD⊥平面ABCD。理由如下:
連接AC交BD于點O,連接EO,如圖12。由△AOB∽△COD,且CD=2AB,得CO=2AO,所 以PE∶EC=AO∶CO=1∶2,則PA∥EO。又PA⊥平面ABCD,所以EO⊥平面ABCD。又EO?平面EBD,平面ABCD∩平面EBD=BD,所以平面EBD⊥平面ABCD。
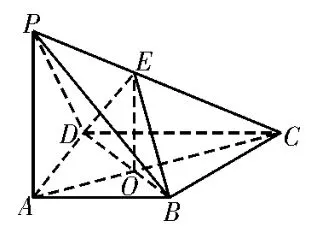
圖12
點撥:要證明面面垂直,就要在平面EBD中尋找平面ABCD的垂線,因為PA⊥平面ABCD,所以要在平面PAC內過E點作PA的平行線,利用△AOB∽△COD,得到等比例,從而PA∥EO,結論得證。

