信息論與編碼課程理論聯(lián)系實(shí)際教學(xué)模式的探索
姑麗加瑪麗·麥麥提艾力,艾斯卡爾·肉孜
(1.新疆師范大學(xué)數(shù)學(xué)科學(xué)學(xué)院,新疆 烏魯木齊 830017;2.新疆大學(xué)數(shù)學(xué)與系統(tǒng)科學(xué)學(xué)院)
0 引言
信息論與編碼是一門培養(yǎng)學(xué)生應(yīng)用概率論、隨機(jī)過程、數(shù)理統(tǒng)計(jì)和近代代數(shù)的方法來研究廣義的信息傳輸、提取和處理一般規(guī)律的專業(yè)方向課程,是信息、通信和計(jì)算機(jī)等專業(yè)培養(yǎng)方案中的主干課程[1]。
國家對網(wǎng)絡(luò)信息安全十分重視[2-3]。信息安全作為網(wǎng)絡(luò)空間安全一級學(xué)科的重要學(xué)科專業(yè),承擔(dān)著為國家培養(yǎng)人才的重任,以培養(yǎng)出具有良好的數(shù)學(xué)基礎(chǔ)和數(shù)學(xué)思維能力、能解決信息技術(shù)和工程計(jì)算中的實(shí)際問題的高級專業(yè)人才。
信息論是一門與通信系統(tǒng)理論有著密切關(guān)系的學(xué)科[4],邏輯推理過程較多,相對比較枯燥,涉及的知識點(diǎn)繁雜、理論性強(qiáng),內(nèi)容比較抽象,加之大量的數(shù)學(xué)公式以及相關(guān)定理,教學(xué)難度系數(shù)較高[5]。從目前的教學(xué)狀況看,學(xué)生對于信息論的產(chǎn)生和發(fā)展歷史不夠了解,對信息的數(shù)學(xué)模型的轉(zhuǎn)換理解度不夠,學(xué)習(xí)的編碼理論無法應(yīng)用于實(shí)踐,達(dá)不到學(xué)以致用的目的。因此在教學(xué)過程中適當(dāng)引入實(shí)際應(yīng)用案例,不僅可以豐富課堂內(nèi)容,也可以激發(fā)學(xué)生的學(xué)習(xí)熱情,讓學(xué)生積極參與到課堂中,促進(jìn)師生之間的互動(dòng)交流。
結(jié)合幾年的教學(xué)經(jīng)驗(yàn),本文嘗試用信息論與編碼課程一些靈活的教學(xué)方法,通過實(shí)際的案例應(yīng)用,將學(xué)生帶入實(shí)際應(yīng)用問題的場景中,在解決實(shí)際問題的過程中學(xué)習(xí)知識,提高學(xué)生的課堂參與度和興趣,培養(yǎng)學(xué)生獨(dú)立思考的能力,促進(jìn)學(xué)生體會信息論與編碼課程的現(xiàn)實(shí)意義和理論價(jià)值。
1 內(nèi)在關(guān)系及案例引導(dǎo)
信息論與編碼課程內(nèi)容主要包括信息傳輸系統(tǒng)、信息的定義和度量、離散信源和連續(xù)信源的信息熵、信道和信道容量、平均失真度和信息率失真函數(shù)、信源編碼、信道編碼等。課程核心內(nèi)容圍繞無失真信源編碼定理、信道編碼定理、限失真信源編碼定理為主要脈絡(luò)的香農(nóng)三大極限定理以及香農(nóng)公式展開。
從信息傳輸系統(tǒng)的基本原理可以給學(xué)生講解課程內(nèi)容之間的內(nèi)在聯(lián)系和香農(nóng)三大定理的實(shí)際意義。首先舉幾個(gè)實(shí)際應(yīng)用例子,給學(xué)生提出思考問題,比如:在日常生活中我們最常見的信息傳輸設(shè)備是手機(jī),那么手機(jī)信息傳輸?shù)幕驹頃鞘裁礃拥模啃畔鬏斚到y(tǒng)中的信源和信宿可以比喻打電話和接電話的雙方,由圖1可以解釋信息傳輸系統(tǒng)的基本原理。
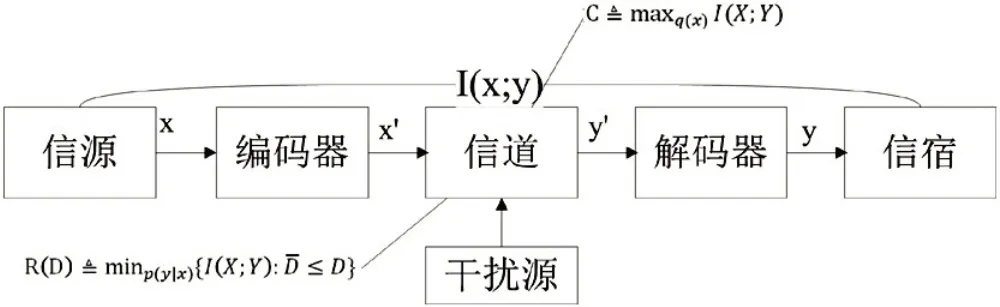
圖1 數(shù)字通信系統(tǒng)
從打電話到接電話的過程中信息傳輸?shù)耐ǖ婪Q為信道,信息傳出后到達(dá)信道之前需要解決三個(gè)問題:模擬和數(shù)字信號之間的轉(zhuǎn)換;提高信息傳輸率R(信源編碼器的主要功能);增加可靠性,降低出錯(cuò)概率pe→0(信道編碼器的主要功能)。
為提高信息傳輸率,根據(jù)香濃第一定理(式1),平均編碼長度nˉ大于平均符號熵H(x)時(shí)才可以得到唯一可譯碼,但同時(shí)要滿足盡可能短的要求,不能超過H(x)+1,這樣才可以得到最好的編碼效率η=H(x)。
信道的基本原理可以比喻高速公路,每個(gè)道路都有最低和最高限速,信息傳輸通道也一樣。根據(jù)香濃第二定理:當(dāng)編碼長度n →∞時(shí),錯(cuò)誤概率pe≤e-nE(R) →0,可靠性函數(shù)E(R)在0 <R<C的范圍內(nèi)為正。香濃第二定理說明信息傳輸率R要小于信道容量,也就是信道所能容納的最大信息量,才能保證可靠傳輸(pe→0)。信道編碼是有目的地增加碼符號,以進(jìn)行檢驗(yàn)和糾錯(cuò)。
根據(jù)香濃第三定理:當(dāng)R>R(D)時(shí),只有信源序列足夠長,一定存在一種編碼方法,使平均失真≤D+ε,否則,必有≥D。
2 外在關(guān)系
信息論與編碼關(guān)系到概率論、隨機(jī)過程、數(shù)理統(tǒng)計(jì)和近代代數(shù)等多個(gè)專業(yè)課程。相關(guān)定理和公式的證明和推導(dǎo)涉及到的知識點(diǎn)繁雜,比較抽象并需要邏輯推理。上課的過程中通過講解生活中隨處可見的實(shí)例,聯(lián)系公式理論上可以使學(xué)生更易于理解概念的內(nèi)在本質(zhì),從而將理論應(yīng)用到實(shí)踐中去。
⑴信息論與概率的關(guān)系
信息的度量方法是信息論與編碼課程中最基本的內(nèi)容,根據(jù)概率論的基本知識和貝葉斯公式可以很容易給學(xué)生講解基本概念和公式推導(dǎo)。比如:給出兩個(gè)一周天氣預(yù)報(bào)的信源x={晴,晴,晴,晴,晴,晴,晴}和x’={晴,晴,晴,雪,晴,晴,晴},從這兩個(gè)信源可以看出x’的信息量比x 大I(x′) →∞,因?yàn)閤’(4)=’雪’跟前后信源的差別很大、相關(guān)性小、發(fā)生概率小q(x′) →0。事件x很常見q(x)→1,因此信息量小I(x′)→0。從這個(gè)例子可以推導(dǎo)信息量是概率的遞減對數(shù)函數(shù),因此可以得到自信息量的公式對I(xi)進(jìn)行求平均得到信息熵互信息量I(xi;yj)是信源x 和信宿y 相互通信之后的信息量,從x 和y 的不同角度可以推導(dǎo)I(xi;yj)的公式,從x的角度分析,x通信之前的不確定性I(xi),收到y(tǒng) 之后對x 仍存在的不確定性用I(xi|yj),x 和y 之間的通信過程是這兩個(gè)不確定性減少的過程,由此可以得到互信息量公式(式⑵),同樣從y 和xy 的角度可以得到另外兩種表達(dá)式(式⑶和式⑷)并對其進(jìn)行統(tǒng)計(jì)平均可以得到I(x;y)和H(x)之間的關(guān)系式(式⑸~式⑺)。由式⑸~式⑺可以得到維拉圖(圖2),從維拉圖中可以看出通信過程中發(fā)送的實(shí)際有意義的信息量由I(x;y)來度量,圖2 右邊的蘋果標(biāo)志在信息論角度上指出通信過程中實(shí)際傳輸?shù)男畔⒘俊?/p>
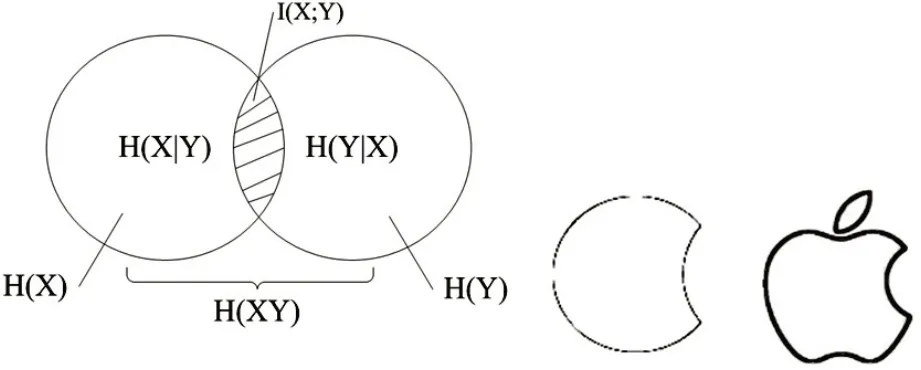
圖2 維拉圖
利用全概率公式可以證明互信息量和信息熵之間的關(guān)系式。下面給出式⑸的證明方法,其他公式也可以類推。
⑵信息論與線性代數(shù)的關(guān)系
信息論與編碼中,線性分組碼是整個(gè)糾錯(cuò)碼中很重要的一類碼。從線性分組碼的基本概念和編碼方法中可以直觀的體會線性代數(shù)的相關(guān)知識在信息論與編碼中的重要性。線性分組碼中每一個(gè)碼字v可以看成是以輸入信息u作為系數(shù)的基向量的線性組合:

矩陣G 為線性分組碼的生成矩陣。線性分組碼(n,k)是由矩陣G 的行向量張成的子空間,由秩零化度定理可知,矩陣G 的零空間N(G)的維度為n-k。因而可以找出n-k 個(gè)線性獨(dú)立的向量,h0,h1,h2,...,hn-1張成了G的零空間N(G)。
可以得出:
矩陣H為線性分組碼的校驗(yàn)矩陣。如(7,4)漢明碼信息位為4 位,監(jiān)督位為3 位,監(jiān)督位有2 × 3=8 種組合。可能發(fā)生的結(jié)果如下:

根據(jù)碼元錯(cuò)誤與校正子的關(guān)系可以列出監(jiān)督方程,如S1與a6,a5,a3,a2有關(guān)。漢明碼的監(jiān)督方程為:
監(jiān)督矩陣:
碼組向量:
記為:H·AT=0
根據(jù)監(jiān)督方程確定了編碼方程:
兩邊同時(shí)取轉(zhuǎn)置:
其中Q=PT,然后得到生成矩陣G=[Ik×k;Q],所以編碼矩陣方程為
生成系統(tǒng)碼形式的漢明碼的生成矩陣為:
3 實(shí)踐環(huán)節(jié)
信息論與編碼這門課不是簡單的傳授理論知識需適當(dāng)安排相關(guān)編碼計(jì)算任務(wù)和上機(jī)實(shí)踐。平均編碼長度在滿足香濃第一定理的范圍之內(nèi)可以對同一個(gè)信源找出不同的編碼序列并可以得到不同編碼效率,可以給學(xué)生安排對同一個(gè)信源找出最好的編碼效率的任務(wù),學(xué)生根據(jù)自己學(xué)過的相關(guān)定理和編碼方法,在尋找最好的編碼效率的過程中發(fā)現(xiàn)問題和不懂的地方,這樣一方面可以鞏固相關(guān)知識,另一方面可以提高學(xué)生的計(jì)算、解決問題和邏輯思維能力。編寫代碼是學(xué)好這門課的重要途徑,比如信源編碼和信道編碼,在書本上學(xué)習(xí)原理和實(shí)現(xiàn)方法后要上機(jī)實(shí)驗(yàn),最終得到運(yùn)算結(jié)果才可以更清楚編碼方法的邏輯、具體實(shí)現(xiàn)流程和實(shí)際應(yīng)用等,同時(shí)可以弱化學(xué)生的機(jī)械計(jì)算,加強(qiáng)學(xué)生的動(dòng)手能力和應(yīng)用能力。
4 總結(jié)
本文結(jié)合教學(xué)經(jīng)驗(yàn),主要討論信息論與編碼課程教學(xué)中理論聯(lián)系實(shí)際的一些靈活的教學(xué)方法,幫助學(xué)生更好地理解數(shù)字通信系統(tǒng)的基本原理,同時(shí)理解與其他課程之間的聯(lián)系,這有助于推導(dǎo)各相關(guān)公式和證明。針對實(shí)踐教學(xué)環(huán)節(jié),分別討論了安排編碼計(jì)算任務(wù)和上機(jī)實(shí)踐等教學(xué)手段,在編碼方面,同一題可以用不同的編碼來解,以此讓學(xué)生在解決實(shí)際問題的過程中學(xué)習(xí)理論知識,可以提高學(xué)生的課堂參與度和興趣,培養(yǎng)學(xué)生獨(dú)立思考的能力,促進(jìn)學(xué)生體會信息論與編碼課程的現(xiàn)實(shí)意義和理論價(jià)值。

