近水面拖曳浮標測試系統運動特性研究

張 錦，鄧玉聰，鄭孝彬，王建軍

(1. 華中科技大學 船舶與海洋工程學院，湖北 武漢 430074；2. 中國船舶集團有限公司七五〇試驗場，云南 昆明 650101)

0 引 言

目前水下通信大多利用長波、水聲、激光、中微子等方式進行，但都存在一定的缺點。通信浮標技術使潛艇不浮出水面，就能直接與衛星或者基站高速通信，避免了采用自航器帶來的水聲通信噪聲高、傳播損失大等缺點的同時，滿足了潛艇隱蔽性的需求[1]。但通信浮標長時間暴露于水面會產生尾跡，為了解決此問題，提出一種二級拖曳通信浮標，工作狀態的拖曳通信浮標天線高出波浪表面一定距離，而二級拖體隱蔽在水下。

潛艇拖曳通信浮標在部署之前需要經過測試獲得準確的動力學特性。Jagadeesh 等[2]利用1∶2 的AUV 模型在拖曳水池中進行拖曳試驗，得到了AUV詳細的水動力學數據。杜曉旭等[3]基于集中質量法，將拖纜首段的張力影響計入水下航行器的運動方程，分析了拖纜對航行器操縱性能的影響。沈建森等[4]建立了水下航行器的動力學模型并設計了舵控制器控制其在水下的深度，仿真結果與航行器實際的運動規律相吻合。金良安等[5]將一級拖曳系統視為一個整體，將拖纜力作為中間量實現拖船、拖體和拖纜三者的耦合，分析了拖纜和拖體對拖船操縱性能造成的影響。拖曳母船在海洋風浪等因素的干擾下會產生無規則運動從而影響整個拖曳系統，王海波等[6]設計一種波浪補償裝置，保持了拖曳點位置的穩定。上述拖曳系統中的拖體均工作在水下一定深度，不會受到波浪的直接作用，與本文中的拖曳浮標工作在近水面有很大不同，因此需要對拖曳系統測試平臺進行動力學建模與仿真分析研究。

本文利用拖船與升沉補償裝置、一級拖體、一級拖纜搭建一種測試平臺，該測試平臺可以模擬潛艇水下的運動，并且可調節其拖曳速度與拖曳深度。以安裝有可折疊天線并配備深度模糊控制器的通信浮標為測試對象，為了得出合適的拖曳參數，首先建立測試平臺及被測對象的動力學模型，在Matlab/Simulink 中將測試平臺與被測對象相耦合，并建立不同拖曳速度與不同拖纜長度條件下的拖曳試驗仿真模型。最后根據仿真結果，分析上述因素對拖曳系統試驗平臺的影響。

1 測試系統結構及其動力學模型

1.1 測試系統結構及坐標系定義

為對拖曳通信浮標進行測試，本文提出如圖1所示的測試系統，該系統包括測試平臺和被測對象。測試平臺由拖船與升沉補償裝置、一級拖體、一級拖纜組成，通過二級拖纜與一級拖體連接的二級拖體（即拖曳通信浮標）為被測對象。升沉補償裝置安裝在拖船甲板上,負責補償拖船由于波浪影響在垂直方向產生的升沉位移。一級拖體為大型沉降器，用于模擬潛艇的運動。

圖1 測試系統結構示意圖Fig. 1 Structure diagram of the test system and its coordinate system

測試系統的坐標系定義見圖1，慣性坐標系O0X0Y0Z0的原點為拖船升沉補償點所處的初始位置，被測對象拖曳浮標的隨體坐標系OXYZ的原點為其浮心處。慣性坐標系與隨體坐標系之間通過歐拉角相互轉換。

1.2 一級拖體和拖纜動力學模型

一級拖體在測試系統中主要起壓載和穩定作用，以實心鐵球作為一級拖體，質量為5 000 kg，體積為0.62 m3，直徑為1.07 m。

一級拖體為球狀且與拖纜鉸鏈連接，忽略其姿態變化，其動力學模型簡化為在慣性坐標系下的三自由度動力學模型，如下式：

式中：F1為一級拖體所受外力，包括流體阻力、重力、浮力、兩段拖纜的作用力；m1為一級拖體的質量及附加質量；U1=[u1v1w1]T為一級拖體在慣性坐標系下相對海流的速度矢量。

實際拖曳過程中，一級拖纜為鋼纜，其剛度較大，且其所承載的拉力遠大于所受流體阻力，將一級拖纜近似為彈簧阻尼模型[7]，并建立動力學模型，如下式：

式中：FT為一級拖纜的拉力； Δl1s為一級拖纜長度的變化；為一級拖纜的彈簧常數；ks為一級拖纜拉力判定系數；cs為 一級拖纜的阻尼系數； Δus為一級拖纜兩端的速度差的絕對值；Ac為一級拖纜在自然狀態下的橫截面積；l1s為一級拖纜在自然狀態下的長度。

試驗選用的一級拖纜長度直徑為0.017 m，彈性模量為1010Pa。

1.3 二級拖體動力學模型

二級拖體采用流線型結構，如圖2 所示。主體有2 對可變角度的前后翼、2 個固定的垂直尾翼，其中上方尾翼為天線安裝平臺。拖曳點位于拖體下方三角形鋼架上，與二級拖纜連接。

圖2 二級拖體結構Fig. 2 The structure of the secondary drag body

二級拖體的主要參數如表1 所示。

表1 二級拖體物理參數Tab. 1 Physical parameters of the tested body

基于水下航行器六自由度動力學模型[8]，并考慮到拖曳過程中海流相對拖體的速度，建立的被測對象在隨體坐標系下的動力學方程，如下式：

式中：FΣ為二級拖體所受外力；u，v，w為二級拖體相對海流的速度矢量； Ω=[p q r]T為二級拖體角速度矢量；RG為二級拖體重心位置；TΣ為二級拖體所受外力矩；I為二級拖體的慣性矩陣；U為二級拖體的速度矢量相對海流的速度矢量。

1.4 二級拖纜動力學模型

二級拖纜為臍帶纜，剛度比鋼纜小，因此作為柔性連接介質，采用凝聚參數法建立其動力學模型，建模前進行如下簡化：

1）忽略拖曳過程中二級拖纜的彎曲剛度；

2）忽略拖曳過程中二級拖纜的扭轉。

凝聚參數法的建模思想如圖3 所示。將二級拖纜等分分段的受力以及分段質量集中于二級拖纜的等分點上，每個分段的拖纜都簡化為彈簧模型[9]。在未受拉力狀態下，將二級拖纜沿其軸向平均等分為20 份，二級拖纜首尾處的端點質量為二級拖纜總質量的1/40，第2～20 個等分點的質量則為二級拖纜總質量的1/20。不考慮二級拖纜的扭轉，在慣性坐標系下建立二級拖纜動力學模型。

圖3 凝聚參數法對二級拖纜建模示意圖Fig. 3 Schematic diagram of towed cable by lumped mass method

二級拖纜動力學模型如下式：

式中：msi為臍帶纜節點i的質量；lsi為臍帶纜節點i的位置；Fsi為 臍帶纜節點i所 受凈浮力；fsi為臍帶纜節點i所受水阻力；Tsi為 臍帶纜節點i與 節點i-1之間的拉力。

通過對式(7)進行迭代求解，可得到二級拖纜各等分點處作用力以及各等分點位置坐標，將各等分點依次相連可近似得到二級拖纜的整體形態。

二級拖纜等分點所受流體阻力計算公式如下式：

式中：li為 二級拖纜等分段的長度；di為二級拖纜等分段的直徑；Cti為 二級拖纜切向阻力系數；Cni為二級拖纜法向阻力系數；URti為二級拖纜等分點i相對于流體的切向速度；URni為二級拖纜等分點i相對于流體的法向速度。

二級拖纜等分點之間的拉力計算公式如下式：

式中，Ei為二級拖纜的彈性模量。

試驗選用的二級拖纜直徑為0.018m，彈性模量為109Pa。

1.5 附加質量和波浪力動力學模型

1）附加質量

二級拖體的運動會導致其受到周圍流體的慣性阻力，等價于二級拖體質量的增加。二級拖體所受流體慣性阻力與二級拖體加速度的比例系數為附加質量，由于二級拖體關于XOZ面對稱，其矩陣形式可簡化表示為：

式中：附加質量 λi j中的下標i表示二級拖體所受慣性阻力或力矩的方向，j表示二級拖體平動速度或者角速度的方向，數字1,2,3 表示分別二級拖體在OX,OY,OZ方向的受力或者加速度，數字4，5，6 表示分別表示二級拖體繞隨體坐標系OX,OY,OZ軸的力矩或者角加速度。

2）波浪力

為支撐通信天線浮出海面，二級拖體需要在近海面運行，因此波浪力是不可忽視的影響因素。二級拖體所受的波浪力以及波浪力矩利用Morison 方程求解。采用線性波模型對波浪進行建模，在慣性坐標系下波浪內部水質點速度分布如下式：

式中：uw,vw分別為波浪水質點在慣性坐標系下水平方向和垂直方向的速度；Aw為線性波波幅；kw為線性波波數； ωw為 線性波角頻率；x2為二級拖體在慣性坐標系下的x方向坐標；z2為二級拖體在波面下的深度；h為慣性坐標系下所處海域的深度；t為時間。

2 二級拖體控制方法

為了提高潛艇的隱蔽性，二級拖體要始終位于波面之下0.8±0.3 m 工作，僅使通信天線發射部位處于海面之上一定高度。

2.1 二級拖體深度和姿態控制

基于模糊PID 算法的二級拖體前翼控制器可以通過檢測相對于波面的實時深度控制前翼，進而控制二級拖體的深度，使其保持在合適位置。

二級拖體深度控制系統結構如圖4 所示。將二級拖體深度誤差e和深度誤差變化率ec進行模糊化后，解模糊后輸出PID 控制器的修正參數：比例修正系數ΔKp，積 分 修 正 系數 ΔKi，微分 修 正 系數 ΔKd，這3 項修正系數分別與PID 控制器中的比例系數Kp，積分系數Ki，微分系數Kd進行線性疊加，從而實時整定PID 控制器的參數。

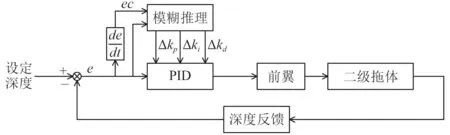
圖4 模糊PID 深度控制結構Fig. 4 Deep control structure based on fuzzy PID

式中：u(t)為PID 控制器的輸出即二級拖體前翼角度；e(t)為PID 控制器的輸入即二級拖體相對于波浪表面的深度與期望深度的實時誤差；Kp,Ki,Kd分別為模糊算法整定后的比例系數、積分系數和微分系數；Kp0,Ki0,Kd0分別為PID 控制器初始狀態下設置的比例系數、積分系數和微分系數； ΔKp, ΔKi, ΔKd分別為經過模糊推理得到的修正比例系數、修正積分系數和修正微分系數。

基于PID 算法的二級拖體后翼控制器通過檢測自身姿態對后翼翼角進行調整，進而控制二級拖體的姿態。在拖曳過程中對波面的追蹤可能會導致自身姿態頻繁變化，為避免PID 算法出現飽和的情況，采用去掉積分環節即PD 控制器對二級拖體的姿態進行控制，其結構如圖5 所示。

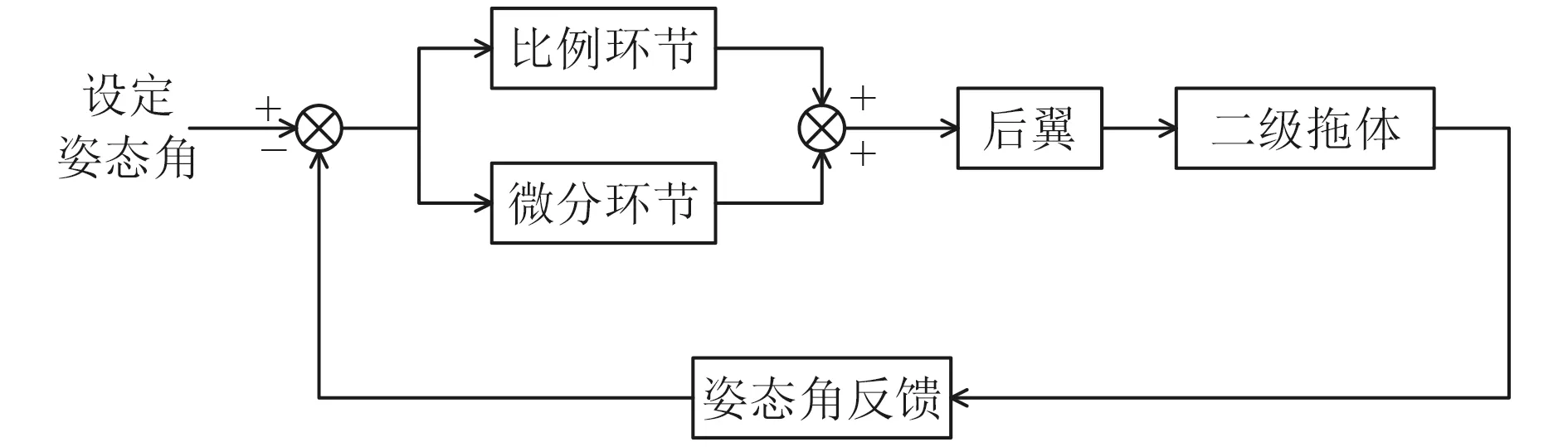
圖5 PD 姿態控制結構Fig. 5 PD-based attitude control architecture

采用試湊法對后翼的PD 控制器進行整定，其數學表達式如下式：

式中：uθ(t) 為 PD 控制器的輸出即后翼角度；eθ(t)為PD 控制器的輸入即二級拖體實時姿態角與期望姿態角的誤差；Kθp為 比例系數；Kθd為微分系數。

3 二級拖體模型試驗

為了得到二級拖體水動力系數，采用模型拖曳試驗測量二級拖體的阻力系數，同時對二級拖體進行流體仿真。模型利用3D 打印技術按照3.5 的縮尺比打印成型。在得到模型的相關阻力系數后利用二因次換算法換算成二級拖體的實際阻力數據。

根據附加質量的定義，設定二級拖體在流場中做1 m/s2的加速平動和0.1 rad/s2的加速轉動，仿真得出二級拖體受力。根據試驗結果，得到如表2 所示的二級拖體水動力系數；根據仿真結果，得到如表2 所示的附加質量系數。

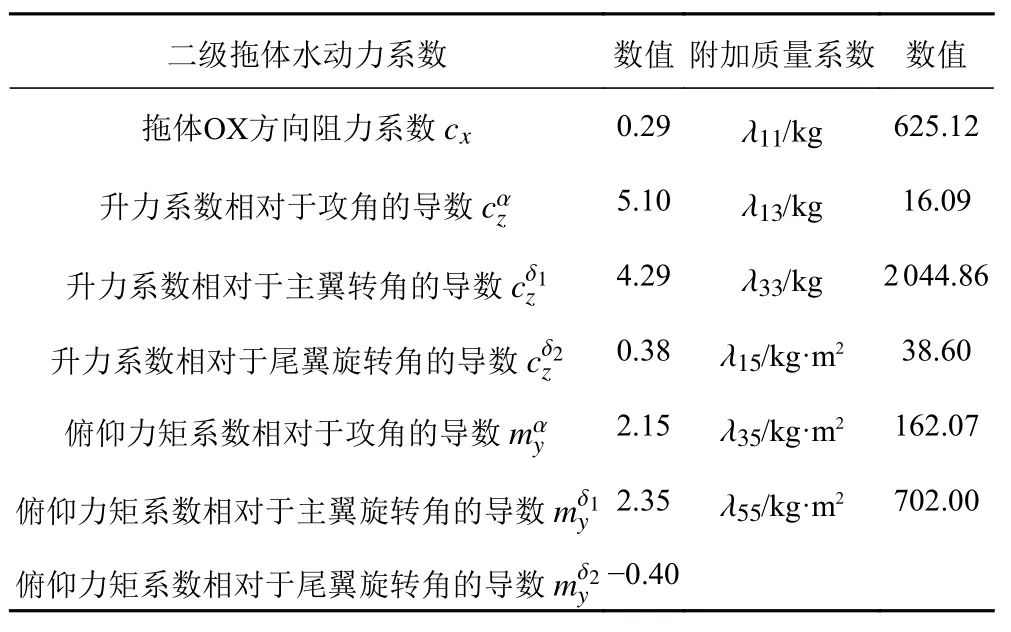
表2 二級拖體水動力系數及附加質量系數Tab. 2 Hydrodynamic coefficient of secondary drag body and coefficient of added mass

4 系統仿真結果分析

4.1 仿真模型及模擬工況

在Matlab/Simulink 中搭建了測試平臺的仿真模型，其模擬工況為：測試平臺在4 級海況下，分別以1 m/s，3 m/s，5 m/s 的拖曳速度；長度為60 m，70 m，80 m 的一級拖纜以及長度為150 m，200 m，250 m 的二級拖纜，拖曳對象正對波浪勻速行駛。

4.2 拖曳速度對測試平臺影響

設定測試平臺的二級拖纜長度為200 m，一級拖纜長度為 80 m，在1 m/s，3 m/s，5 m/s 拖曳速度下，一級拖體與二級拖體的運行深度分別如圖6、圖7 所示。

圖6 不同拖曳速度下一級拖體深度對比Fig. 6 Depth of the ballast under three towed velocity

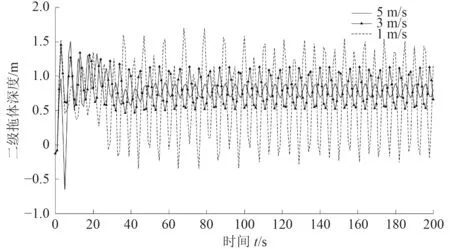
圖7 不同拖曳速度下二級拖體深度對比Fig. 7 Depth of the tested body under three towed velocity

當拖曳速度為1 m/s 時，一級拖體穩定后的運行深度為8 0.6 5 ～8 0.8 1 m，二級拖體的運行深度為-0.23～1.53 mm，此時最大深度導致二級拖體搭載的天線不能正常工作，而且在最小深度時拖體已經露出波面。以3 m/s 和5 m/s 拖曳速度工作時，一級拖體的運行深度分別為71.97～72.04 m 和52.59～52.69 m，二級拖體的運行深度分別為0.53～1.13 m 和0.67～0.89 m。

分析表明，拖曳速度變化對一級拖體的穩定深度具有較大影響，隨著拖曳速度增加，水下系統受到流體阻力增加，導致一級拖體的運行深度減小近20%。被測對象的深度變化幅度受波浪力干擾較嚴重，拖曳速度增加后，被測對象前舵的控制力增加，有利于減小其深度波動幅度，改善其深度控制效果。

4.3 一級拖纜長度對測試平臺影響分析

控制其余條件不變，設定一級拖纜長度分別為60 m，70 m，80 m，測試平臺以5 m/s 拖曳速度運動，一級拖體與二級拖體運行深度分別如圖8 和圖9 所示。分析可知，一級拖纜的長度變化對一級拖體和二級拖體的深度無明顯影響。

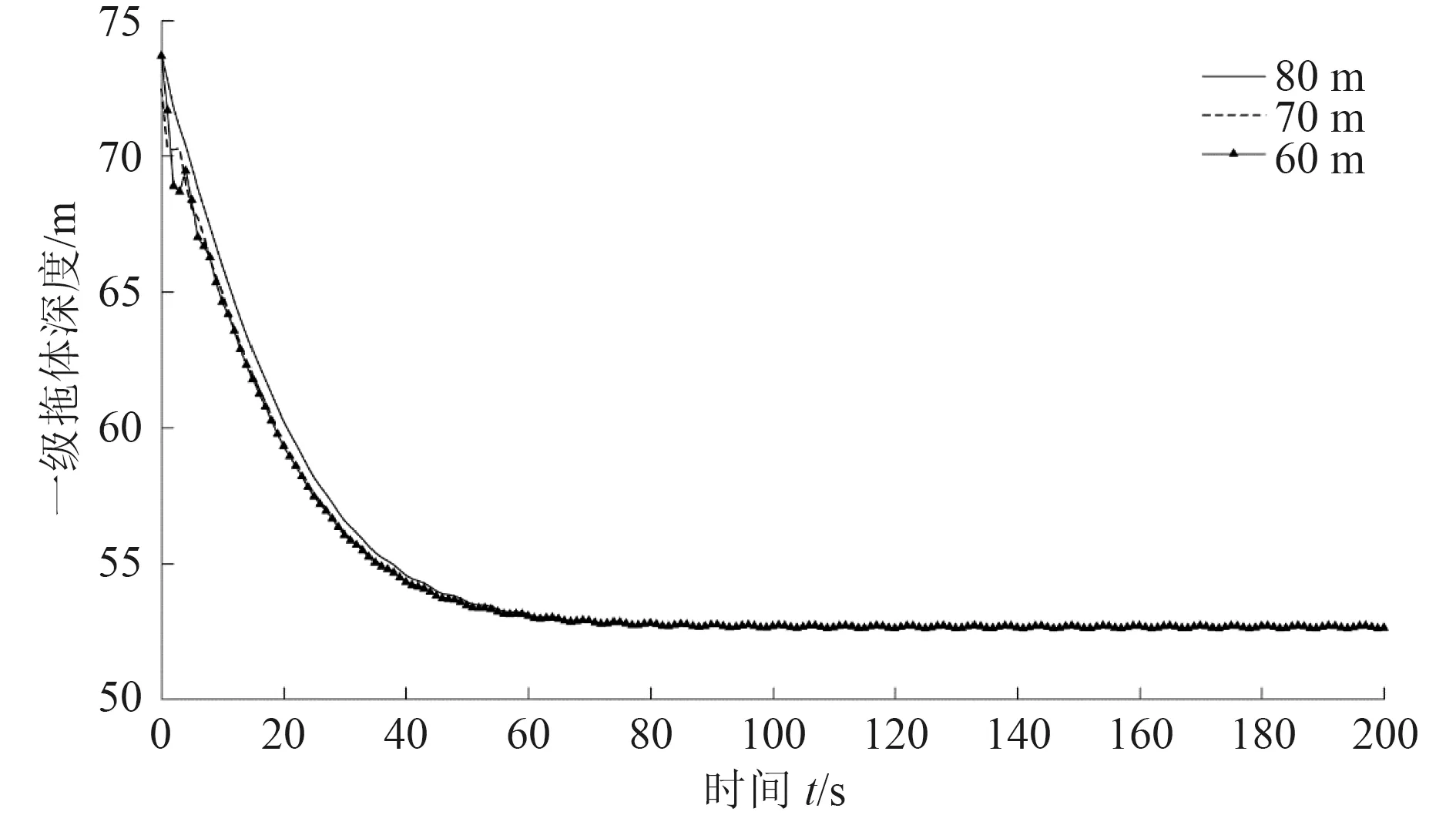
圖8 不同一級拖纜長度情況下一級拖體深度變化對比Fig. 8 Depth of ballast under three lengths of the first-stage flexible towed cable

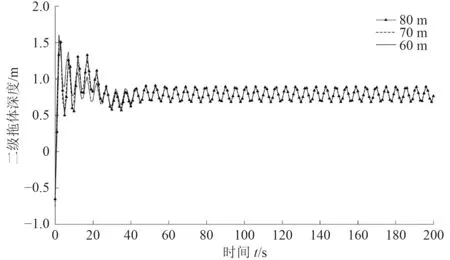
圖9 不同一級拖纜長度情況下二級拖體深度變化對比Fig. 9 Depth of the tested body under three lengths of the first-stage flexible towed cable

4.4 二級拖纜長度對測試平臺影響分析

控制其余條件不變，設定二級拖纜長度分別為150 m，200 m，250 m，測試平臺以5 m/s 的速度拖曳被測對象運動，一級拖體與被測對象運行深度分別如圖10 和圖11 所示。分析可知，增加二級拖纜的長度，被測對象的運行深度仍能保持較高的穩定性，一級拖體的深度變化幅度可達2%以上，但其深度波動幅度受二級拖纜長度影響較小。

圖10 不同二級拖纜長度情況下一級拖體深度變化對比Fig. 10 Depth of ballast under three lengths of the second-stage flexible towed cable

圖11 不同二級拖纜長度情況下二級拖體深度變化對比Fig. 11 Depth of the tested body under three lengths of the second-stage flexible towed cable

5 結 語

為解決潛艇拖曳系統進行運動性能測試時不便直接利用潛艇進行拖曳試驗的問題，提出一種可以模擬潛艇拖曳試驗的測試平臺。首先介紹測試平臺的結構及工作原理，建立測試平臺的動力學模型及仿真模型。

對測試平臺在不同拖曳速度、不同一級拖纜長度以及不同二級拖纜長度下的拖曳試驗進行了仿真分析，根據仿真結果可得到如下結論：

1）拖曳過程中，隨著拖曳速度的增加，一級拖體的穩定深度減小，過渡至穩定狀態的時間增大，但深度變化波動幅度受拖曳速度影響較小。對于被測對象，由于深度控制力隨拖曳速度增加而增大，因此深度波動幅度減小，有利于正常工作。當拖曳速度為1 m/s 或更小時，被測對象的天線已經不能正常工作。

2）拖曳過程中，二級拖纜長度增加，被測對象的穩定深度和深度波動幅度無明顯變化，一級拖體的穩定深度增加，過渡時間增大，深度波動幅度無明顯變化。

3）拖曳過程中，一級拖纜的長度變化對系統無明顯影響。