多主桁鋼桁梁橋橋面荷載橫向分配計算方法研究

韓衍群，侯文崎

(1.中南大學 土木工程學院，湖南 長沙，410075；2.中南大學 高速鐵路建造技術國家工程實驗室，湖南 長沙，410075)

隨著我國國民經濟的快速發展，為了滿足運輸需求，要求橋梁越來越寬。為減小構件規模、降低制造成本，鋼桁梁橋越來越多采用三主桁或多主桁結構形式[1-5]，如武漢天興洲長江大橋、南京大勝關長江大橋均采用多主桁結構形式。

從力學上講，多主桁結構與兩主桁相比，其最大差別是橋面荷載在主桁間分配的不均勻性[6-7]。在兩主桁結構中，均布橋面荷載在橫橋向是等分的。但在多主桁結構中，橋面荷載在主桁間的分配比較復雜[8]。以三主桁結構為例，若不考慮兩邊桁下弦節點剛性，則橋面荷載在三主桁間下弦節點上分配的力學模型相當于帶支座沉降的兩跨連續梁，若主桁間豎向位移相同，則在均布荷載作用下，中桁與邊桁分配的荷載比為10:3。實際上，由于中桁撓度比邊桁的大，橋面荷載在中桁與邊桁分配小于10:3。另外，由于橫聯的作用，使主桁的力從撓度較大的中桁轉移到撓度較小的邊桁，從而使中桁與邊桁的受力差別減小。橋面荷載在主桁間分配的不均勻性將導致主桁間結構內力存在差異，若差異較大，為了結構安全，常采用增大中桁構件截面的辦法來解決，但該方法增加節點與桿件種類，不便于預制與拼裝。目前，國內有些學者對三主桁受力不均勻性進行了研究[9-11]，而國外對這方面的研究很少。劉世忠等[12]通過支座升降技術對內力進行調整，研究了減小受力不均勻性的方法；鮑莉霞[13]采用空間有限元從結構布置角度研究了設置橫聯與否對三主桁結構內力分配的影響，但沒有研究主桁剛度對內力分配的影響，也沒有給出合理剛度；候文崎等[14-16]對三主桁受力特性進行了試驗研究，給出了減小受力差別的一些建議，但對荷載橫向傳遞規律和計算方法研究較少。目前，對二主桁中結構橋面荷載橫向分配計算有可靠的計算公式，而多主桁橋面荷載橫向分配比二主桁復雜得多，對這類橋梁常采用空間有限元法進行分析計算[17-18]。空間有限元法雖然計算精度高，但建模復雜，費時費力，在橋梁設計初期或方案比選時并不是很好的選擇。本文以三主桁鋼桁梁橋為例，從橋面荷載橫向傳遞路徑入手，研究橫向分配的簡化計算模型，并基于能量原理推導橋面荷載橫向分配的計算公式。在此基礎上，利用結構設計不同參數研究主桁間橫向分配不均勻的影響因素，提出合理剛度取值，以便為該類橋梁簡化計算提供依據。

1 橋面荷載橫橋向二次分配

將橋面荷載在下弦節點間的分配稱為第一次分配[20-21]。由于存在三主桁間撓度差，橋面荷載再通過橫聯在3 片主桁間重分配，稱為第二次分配。第一次分配的橋面荷載作用于主桁的下弦節點，而第二次分配的力作用于上弦節點。在實際橋梁中，2次分配是相互關聯、相互影響的，并不是第一次分配完后再進行第二次分配，而是2次分配同時進行，為了敘述方便，下面分別考察2次分配的情況。

1.1 橋面荷載橫橋向第一次分配

若不考慮兩邊桁下弦桿節點剛性，即橫梁與兩邊桁下弦節點鉸接連接，則橫梁的受力相當于1個兩跨連續梁，其力學模型如圖1(a)所示，支座反力即為分配到每片主桁的荷載。三主桁在橋面荷載作用下，以作用均布荷載q為例，由于受力的不均勻性，三主桁豎向存在撓度差，相當于在圖1(a)中的中支座處有一沉降Δ。將圖1(a)中的受力狀態分解為主桁無豎向位移(圖1(b))和主桁有豎向位移(圖1(c))。圖1(b)中只有荷載無支座沉降，而圖1(c)中只有支座沉降無荷載。由結構力學知識可知：圖1(b)中的端支座和中支座反力分別為二者之比為3:10。當圖1(c)中支座產生沉降Δ時，中支座有向下反力而兩端鉸支座的支反力為(其中，E和Ih分別為鋼的彈性模量和橫梁的慣性矩(包括橋面板))。由此可見，由于支座沉降，圖1(a)中支座反力釋放了一部分，而兩端的支座反力增加。

在實際橋梁中，下弦節點對橫梁端部的轉動有一定的約束作用，相當于圖1中兩跨連續梁兩端支座并不是理想的鉸支座，而是能夠承受一定彎矩的彈性支座，這樣，端支座和中支座之間的反力差又減小了一部分。圖1(a)中的3 個支座反力相當于橫橋向3 片主桁下弦節點(下弦桿)對橫梁的支承力，在數值上等于3片主桁下弦節點上分配的橋面荷載，將其稱為橋面荷載的第一次分配。各主桁分配的橋面荷載的比例既與橫梁的線剛度有關，也與三片桁的撓度差Δ有關。

圖1 橫梁受力分解示意圖Fig.1 Mechanical behavior decomposition of transverse beams

1.2 橋面荷載橫橋向第二次分配

3片主桁第一次分配到橋面荷載差別較大，中桁的荷載大，邊桁的荷載小，從而中桁的撓度大于邊桁的撓度。而上部橫聯將3 片主桁聯成一體，抵抗3片主桁間的撓度差，從而產生了橋面荷載橫橋向的第二次分配。

為分析橋面荷載在橫橋向的第二次分配，在主桁節點處橫橋向取出1個橫聯作為隔離體，橫聯上3 個彈簧表示3 片主桁對橫聯的支撐，如圖2所示。與橫梁受力類似，橫聯在3片主桁撓度差Δ下將產生支反力，其大小在邊桁處為，在中桁處為(其中，Ieq為橫聯等效慣性矩)。該反力即橫聯對主桁的作用力與橫聯豎向剛度和三主桁的撓度差有關。橫聯豎向剛度、三主桁間的撓度差越大，橫聯對主桁的作用力越大。

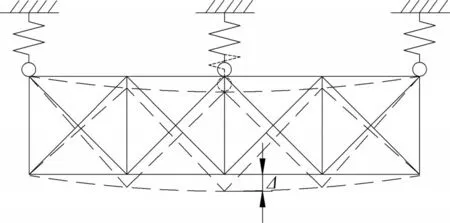
圖2 橫聯受力示意圖Fig.2 Mechanical behavior of lateral bracings

2 橋面荷載橫向分配的簡化模型及計算公式

2.1 橋面荷載橫向分配簡化模型

為分析橋面荷載在橫橋向的二次分配，在主桁節點處橫橋向取出1 個框架作為隔離體，如圖3(a)所示。圖3中，q(x)為橋面荷載，l為桁寬，橫向框架上、下各用3個彈簧表示3片主桁對框架的支撐。每片桁架上下彈簧剛度之和為代表框架所在位置處主桁的豎向剛度，其中，i為下弦節點號，j為桁號，分別為框架在上、下位置主桁的豎向剛度，kij為框架所在位置主桁的總豎向剛度。

kij可按如下方法計算：取第j片主桁，在每個下弦節點作用單位荷載P=1 kN，引起第i個下弦節點豎向撓度為Δij，則定義該節點處彈簧剛度kij=1/Δij。因為不影響橋面荷載的第一、第二次分配[7]，為簡化計算，令相等，均為kij的1/2。

圖3(b)所示為豎桿、橫聯、橫梁的隔離體圖。圖中，豎桿下部所受的力為第一次分配的力，上部所受的力為第二次分配的力。由圖3(b)可見：3片主桁間的橫聯將撓度較大的中桁向上提，而將邊桁向下壓，使主桁上、下節點所受豎向力總和在3片主桁間的差距減小。

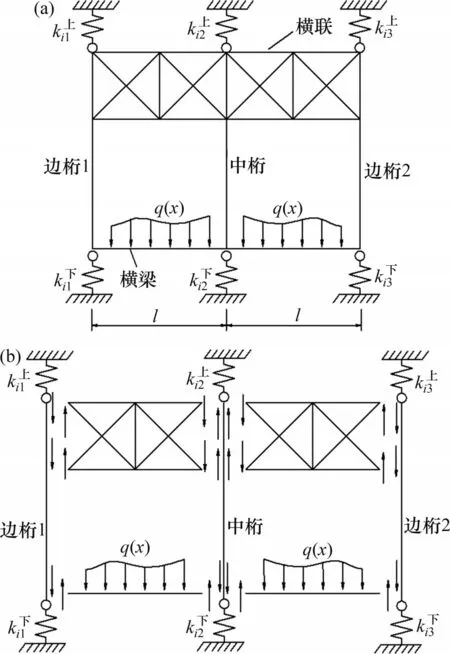
圖3 橫向框架簡化計算模型Fig.3 Simplified calculation model of transverse frame

2.2 計算公式推導

假設：

1)不考慮腹桿軸向變形對三主桁豎向撓度差的影響；

2)兩邊桁的桿件截面相同，即豎向剛度相同；

3)不考慮腹桿、下弦桿對橫梁轉動約束的作用；

4)主桁間的桁寬相同。

在橋面荷載作用下，三主桁鋼桁梁橋的受力可分解為如圖4所示的兩部分：

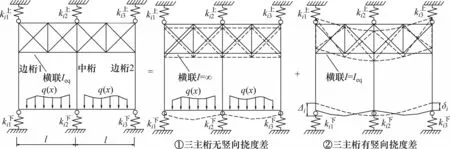
圖4 三主桁鋼桁梁橋受力分解Fig.4 Dissociation of mechanical behavior of three-main-truss steel bridges

① 橫聯剛度無限大，即3 片主桁沒有豎向撓度差；

② 在①變形的基礎上，橫聯剛度由無限剛度變到實際剛度，此時，3 片主桁發生豎向撓度差Δi。

在對稱荷載作用下，在狀態②中，設中桁與邊桁的豎向撓度差為Δi，可得出邊桁處彈簧變形為

式中：Ih為橫梁(包括橋面板)慣性矩；Ieq為橫聯等效慣性矩；l為主桁間的桁寬。由于兩邊桁相同，因此，兩邊桁處彈簧變形相同。

以①的位置為初始位置，②中橫梁(橫聯)的撓度方程為

坐標原點在橫梁(橫聯)最左端，y以向上為正。

則在②中，橫梁的變形能為

橫聯的變形能為

彈簧的變形能為

將式(1)代入式(5)得

外力勢能為

式中：q(x)為外荷載，向上為正。橫向框架總勢能為

式中：Π1為①的總勢能，其與Δi無關；Π2=Uh+Uhl+Ut-V，為②的總勢能，為Δi的函數。由最小勢能原理得

將式(3)，(4)和(6)代入式(10)得

第一次分配到3片主桁的荷載為

第二次分配到3片主桁的荷載為

分配到每片主桁上的總荷載為

當受偏載作用時，可將荷載分解為對稱荷載與反對稱荷載的疊加，對稱荷載下的橫向分配可按式(14)計算。在反對稱荷載作用下，根據對稱結構的受力特性可知，橋面荷載全部分配到兩邊桁上，中桁不分配荷載，即

則偏載作用下分配到每片主桁上的總荷載為

由式(11)和(14)可以看出，當主桁豎向剛度越大即ki越大時，Δi就越小，則分配到邊桁的荷載越少，分配到中桁的荷載就越多；相反，當主桁豎向剛度越小即ki越小時，Δi就越大，則分配到邊桁與中桁上的荷載越接近。因此，越靠近支座處，分配到邊桁與中桁上的荷載差值越大；越靠近跨中，分配到邊桁與中桁上的荷載越接近。橫向聯系(包括橫聯、橫梁、橋面板)豎向剛度越大，三主桁間分配的荷載越接近，因此，橫向聯系具有合適的豎向剛度是減小主桁間受力不均勻的關鍵。在實際橋梁中，橫聯豎向剛度一般比橫梁(包括橋面板)剛度大很多，因此，橫聯豎向剛度是影響橋面荷載橫向分配的主要因素之一[7]。

3 算例驗證

以某(84+84)m兩跨連續三主桁鋼桁梁橋為例，節間長度為12 m，N 型桁架，橋面橫橋向寬度為(15+15)m，如圖5所示。該橋三主桁各桿件截面基本相同，即三主桁剛度相同。建立該橋空間有限元模型，保持桿件布置不變，分別改變主桁豎向剛度、橫聯豎向剛度計算出在對稱均布荷載作用下靠近跨中節點位置橋面荷載在三主桁間的分配，同時，用公式計算結果與其對比，計算結果見表1和表2。

圖5 三主桁鋼桁梁橋Fig.5 Structure diagram of the three-main-truss steel bridge

表1 和表2 中：γ1和γ2分別為一片主桁第一次分配、第二次分配的橋面荷載與三主桁2次分配總荷載的比。由于兩邊桁計算結果相同，故邊桁的γ1和γ2與中桁的γ1和γ2存在如下關系：

表1和表2中計算結果僅列出了中桁的計算結果，其中，不均勻度系數。

由表1可見：公式計算得到的橋面荷載在三主桁間第一次分配γ1、第二次分配γ2和2次分配后的計算結果均與空間計算結果較吻合，驗證了公式的正確性；隨著彈簧剛度增加，三主桁豎向撓度差減小，中桁γ1有所增加，中桁γ2逐漸減少。由于橫聯豎向剛度比橫梁豎向剛度大，因此，中桁γ2減少速度大于中桁γ1增加速度，經二次分配后，荷載不均勻度系數α逐漸增加；當彈簧剛度趨于無限大時(即支座處)，α趨于10:3，靠近跨中逐漸減小；當主桁剛度在3.90×104kN/m 以下時，α不超過1.17，即中桁承受的荷載與邊桁差別不大。

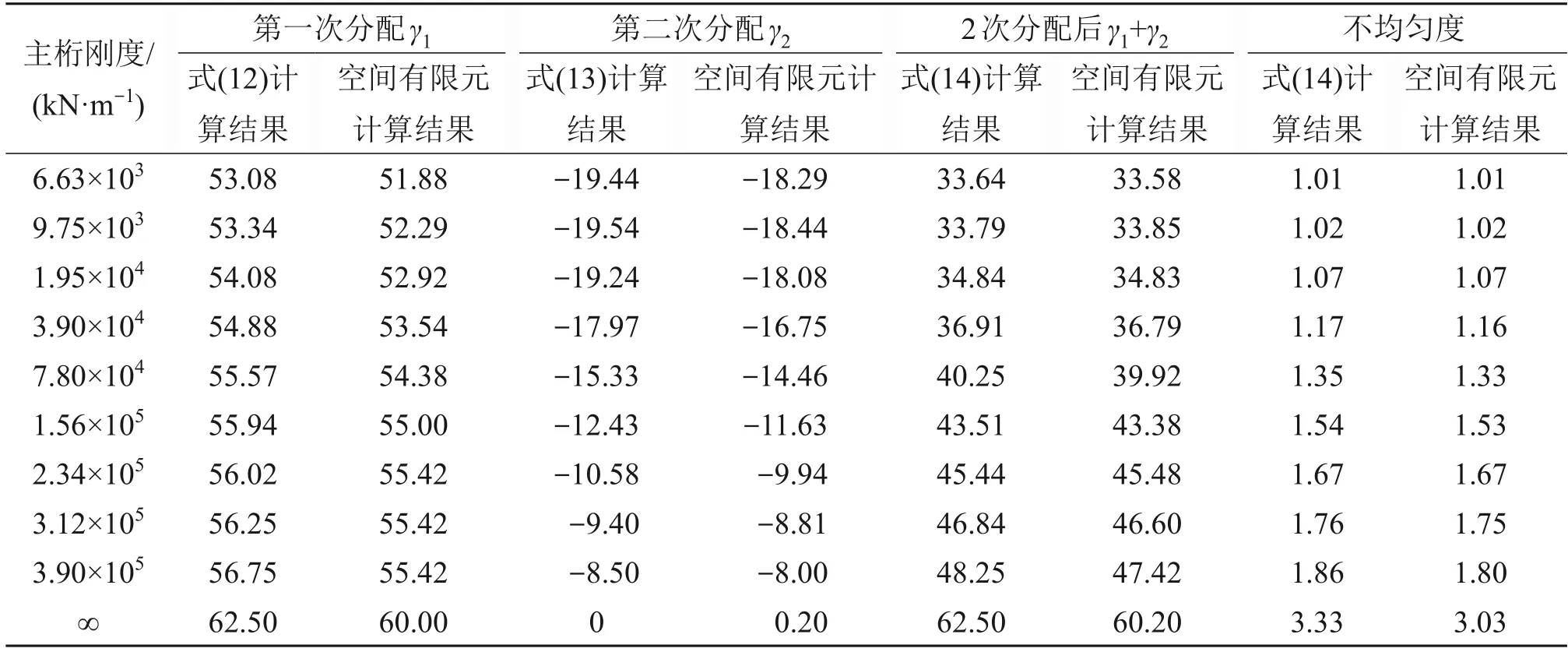
表1 不同彈簧剛度下中桁橫向分配公式計算結果與空間有限元計算結果對比Table 1 Comparison of calculation results of middle truss transverse distribution load formula and spatial finite element results under different spring stiffness

橫聯豎向剛度用其跨中產生單位位移所需的力表示，如圖6所示。圖6中，l為主桁寬度，kh為橫聯豎向剛度。由表2可見：中桁的γ1和γ2隨橫聯豎向剛度的增加而增加，且γ1和γ2增加速度隨橫聯豎向剛度的增加逐漸減小；當橫聯豎向剛度在1.5×105kN/m以下變化時，γ2增加的速度較快；當橫聯豎向剛度大于3.0×105kN/m時，γ2增加的速度較緩慢，因此，橫聯豎向剛度在1.5×105～3.0×105kN/m范圍內比較合理。

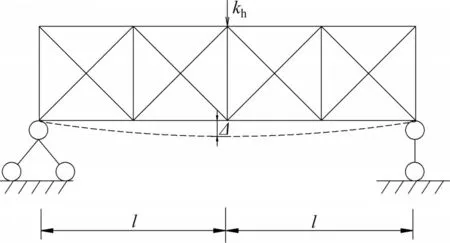
圖6 橫聯豎向剛度示意圖Fig.6 Diagrammatic sketch of vertical stiffness of lateral bracings

表2 不同橫聯剛度下中桁橫向分配公式計算結果與空間有限元計算結果對比Table 2 Comparison of calculation results of middle truss transverse distribution load formula and spatial finite element results under different lateral bracings stiffness

對該橋6 節間縮尺比例為1:6 的試驗模型兩端簡支在試驗荷載(對稱荷載)作用下，采用橫向分配計算公式計算分配到每片主桁的荷載，對每片主桁單獨計算(以下將該法稱為PF 法)，計算每片主桁的撓度和各桿件應力，并將計算結果與空間有限元計算結果和試驗值進行對比，見圖7～9(兩邊桁計算結果相同，故圖7～9僅列出一邊桁的計算結果，坐標原點位于梁的一端)。

圖7 下弦桿豎向撓度Fig.7 Ⅴertical deflection of bottom chords

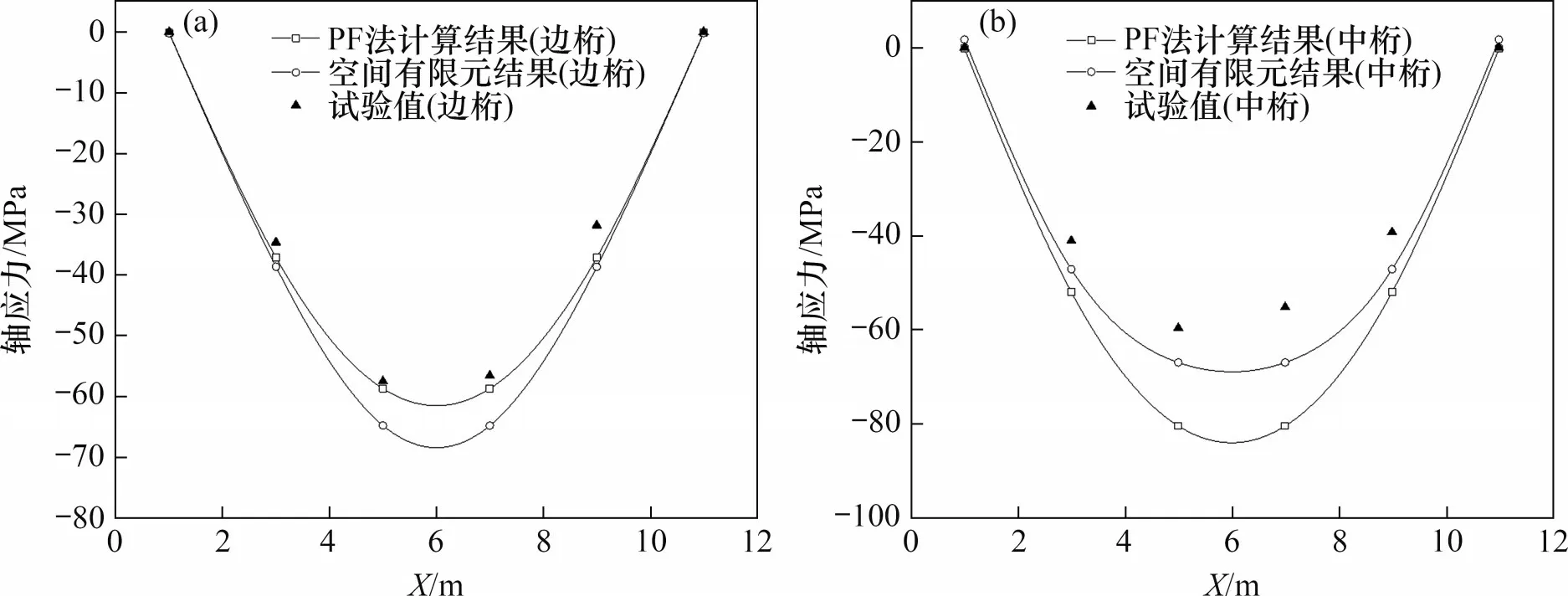
圖8 上弦桿軸應力Fig.8 Axial stress of top chords

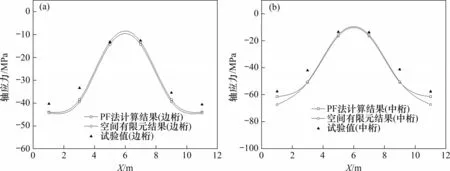
圖9 斜桿軸應力Fig.9 Axial stress of diagonal bar

由圖7～9 可見：采用PF 法所得邊桁、中桁撓度計算結果與空間有限元計算結果、試驗值較接近，撓度最大相對誤差在7.3%之內，采用PF法所得邊桁、中桁桿件應力計算結果與空間有限元計算結果、試驗值(除上弦桿中桁外)較接近，應力最大相對誤差在9.4%以內，與空間有限元計算結果和試驗值相比，PF 法所得計算結果中，中桁的偏大，邊桁的偏小。這是由于在實際橋梁中，邊桁下弦節點對橫梁的轉動約束作用大于橫向框架簡化模型對橫梁的轉動約束作用，導致采用式(14)計算的橋面荷載橫向分配中，邊桁的偏小，中桁的偏大，但在橋梁初步設計或方案比選時，公式計算精度可滿足要求。由此可見，由PF 法計算結果與空間有限元計算結果、試驗值均較吻合，說明按照橫向分配計算公式計算每片主桁分配的荷載接近實際情況，驗證了公式的正確性，確定出橋面荷載橫向分配后，多主桁結構可按平面結構進行簡化計算。

4 結論

1)利用式(14)對三主桁橋面荷載橫向分配計算時，所得結果與空間有限元計算結果、試驗值均較吻合，驗證了公式的正確性。

2)橋面荷載在三主桁間橫向分配主要受主桁、橫聯豎向剛度影響。在均布對稱荷載作用下，不均勻度系數α隨主桁豎向剛度增加而增加，在支座處較大，為3.33，靠近跨中逐漸減小。當主桁豎向剛度在3.9×104kN/m 以下時，α不大于1.17；α隨橫聯豎向剛度的增加而減小，橫聯豎向剛度在1.5×105～3.0×105kN/m范圍內較合理。

3)確定橋面荷載橫向分配后，多主桁結構可按平面結構簡化計算。