考慮碰撞效應的近斷層區橋臺-引橋-剛構連續梁橋結構體系減震措施研究

魏俊杰，鄔曉光，盧偉,3，鄢穩定，胡科堅

(1.武漢大學土木建筑工程學院，湖北 武漢，430072；2.長安大學 公路學院，陜西 西安，710054；3.華設設計集團股份有限公司，江蘇 南京，210001)

三跨高低墩剛構-連續組合梁橋在溫度變化和混凝土收縮徐變等常規條件下具有良好的受力特性，但其剛構墩在地震作用下極易發生屈服破壞，伸縮縫處碰撞效應也會明顯加劇，使引橋梁體墩梁相對位移過大，發生落梁的風險增大，需要采取合適的減震措施來優化橋臺-引橋-剛構連續梁橋結構體系的受力情況[1]。

三跨剛構-連續梁橋結構形式特殊，由剛構墩和活動墩組成，目前針對剛構-連續組合梁橋的研究較少且主要集中在抗震設計和動力性能分析等方面[2]。宋曉東等[3]分析了某多跨不對稱預應力混凝土剛構-連續梁組合結構的設計合理性。魏鑫等[4]以羊記溝左線大橋為研究對象分析了不同地震波輸入方向和分析方法對剛構-連續梁橋地震響應的影響。亓興軍等[5]通過建立一座斜交四跨剛構-連續梁橋精細化有限元模型模擬橋梁動態倒塌破壞特性，并分析了主梁的不規則位移和梁端的碰撞現象。劉俊[6]分析了液體黏滯阻尼器、Lock-up 裝置、雙曲面球型減隔震支座、阻尼器以及減震榫對長聯多跨剛構連續梁橋的減震效果。楊孟剛等[7-8]分析了橫向地震激勵下高速鐵路連續梁橋和簡支梁橋與橫向擋塊的碰撞效應。李小珍等[9]發現行波效應對主跨徑大于80 m的剛構-連續梁橋有較大影響。揭志羽等[10]探討了橋墩剛度、橋墩高度、墩梁固結方式、曲率半徑對大跨高墩小半徑剛構-連續梁橋地震響應的影響。綜上可知，現有研究對于考慮碰撞效應的橋臺-引橋-剛構連續組合梁橋結構體系減震設計的參考價值有限。

鑒于此，本文以西寶高速改擴建工程中某橋臺-引橋-剛構連續組合梁橋結構體系為研究對象，分別在橋臺和橋墩布置減震裝置，對比分析各減震方案在普通地震波和近斷層脈沖型地震波作用下的減震效果，并提出針對橋臺-引橋-剛構連續組合梁橋結構體系的減震設計建議，以期為同類型橋梁結構體系減震設計提供參考。

1 工程概況

預應力混凝土剛構-連續組合梁橋結構體系的跨徑布置如圖1所示。下部主墩為單薄壁空心墩，分割墩為雙柱式墩，引橋上部結構為預應力混凝土箱梁，由5 片預制小箱梁通過橫向聯系拼接而成，下部為柱式墩，樁基礎；兩側橋臺均為肋板式橋臺，樁基礎。主橋箱梁采用C55混凝土，引橋箱梁采用C50 混凝土，橋面鋪裝和主橋墩身采用C40 混凝土，其余橋梁混凝土結構采用C30 混凝土。從左往右的墩臺編號依次為0號臺、1號墩、2號墩、3號墩、4號墩、5號墩、6號墩、7號墩、8號墩和9 號臺，1～8 號墩墩高依次為5.50，6.00，10.50，54.95，10.05，6.00，6.00和5.50 m。其中3號和6號分隔墩處設置240型伸縮裝置，0號和9號橋臺處設置80 型伸縮裝置。引橋在橋臺、過渡墩處共設置10 個滑板式橡膠支座，引橋中間墩各設置10 個板式橡膠支座，主橋在過渡墩處各設置2個單向活動盆式支座，3 號活動墩采用3 個單向活動盆式支座。墩臺樁基均采用摩擦樁，橋臺持力層為老黃土，其余樁基持力層為老黃土、粉質黏土、圓礫、細沙和卵石。車輛荷載等級按公路Ⅰ級進行設計。主橋跨越沖溝，溝底較窄且無常規水流，溝底表層土為新黃土。

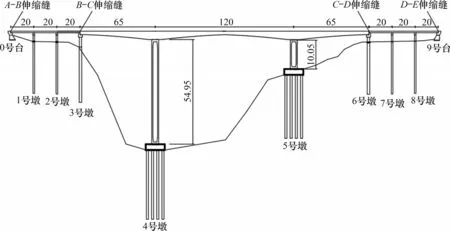
圖1 橋梁總體布置圖Fig.1 General layout of bridge

2 有限元建模和邊界條件模擬

采用CSIBridge 建立全橋結構體系的彈塑性動力分析計算模型，主梁和橋墩采用梁單元，承臺和兩側橋臺采用厚殼單元，采用纖維鉸和P-M2-M3鉸分別模擬引橋橋墩和主橋墩可能出現的非線性行為，無約束混凝土和約束混凝土的材料特性基于Mander 模型[11]獲得，二期鋪裝采用線荷載和面荷載，樁土相互作用采用分層土彈簧進行模擬，土層水平向抗力系數的比例系數m按照規范[12]的建議取值，有限元模型見圖2。

圖2 橋臺-引橋-剛構連續梁橋結構體系彈塑性動力分析模型Fig.2 Elastoplastic dynamic analysis model of abutment approach bridge rigid frame continuous girder bridge structure system

按照“公路橋梁抗震設計規范”中的建議，板式橡膠支座、滑板式橡膠支座和盆式橡膠支座均采用理想彈塑性滯回曲線模擬，伸縮縫處接觸非線性采用組合Kelvin 碰撞單元模擬，碰撞單元剛度取較短主梁軸向剛度的0.5 倍[13]。設KL為Kelvin碰撞單元剛度，Damp和Gap單元剛度KD和KG均取1 000倍KL，保證Damp單元為近似純阻尼單元、縫閉合時KG剛度足夠大且近似剛性，以達到計算收斂和等效模擬Kelvin 碰撞單元的目的。Kelvin碰撞單元及接觸力關系如圖3所示。伸縮縫處碰撞力-位移關系式如下：式中：Δ為伸縮縫初始間隙，根據設計文件取主引橋間距為0.19 m，引橋與橋臺間距為0.06 m；u1和u2分別為地震作用下伸縮縫處相鄰梁體的位移；c為碰撞單元阻尼；v為相對碰撞速度；F為碰撞力。

圖3 Kelvin碰撞單元及接觸力關系Fig.3 Kelvin collision element and contact force relationship

橋臺與臺后填土的接觸關系采用Duncan-Chang 非線性本構關系定義的Multilinear Elastic Link 單元進行模擬[14]，非線性本構關系式和計算結果分別如式(2)和圖4所示。

圖4 橋臺與背土相互作用縱向彈簧模型Fig.4 Longitudinal spring model of interaction between abutment and back soil

式中：p為土體作用于臺背的土壓力；u為臺背后土體的水平位移；Pult是作用于臺背的被動土壓力；K為初始剛度；Rf為經驗系數，本文取0.8。根據工程實際和“公路橋梁抗震設計規范”，計算初始剛度K和被動土壓力Pult。

3 減隔震裝置模擬

根據摩擦鐘擺原理，雙曲面球型摩擦擺支座在小震下可依靠上部自重產生的靜摩擦力保持結構穩定，大震下則通過剪斷銷釘擺動隔震[15]，其力-位移關系如圖5所示。圖5 中，W為豎向自重荷載；R為滑動球面與轉動球面之間球心距；D為設計位移；ν為支座滑動水平速度；H為滑動球面與轉動球面的球心距；μ為滑動球面的摩擦因數；F為支座水平力；Fp為屈服強度；Kb為屈后剛度；Ky為屈前剛度；X為支座水平向位移；Xy為屈服位移。本文采用CSiBridge中Friction Isolation單元進行模擬。研究表明球心距R對結構地震響應影響較小，摩擦因數μ的影響明顯。本文根據工程實際情況選擇摩擦因數μ=0.06，球心距R=0.5 m[8]。

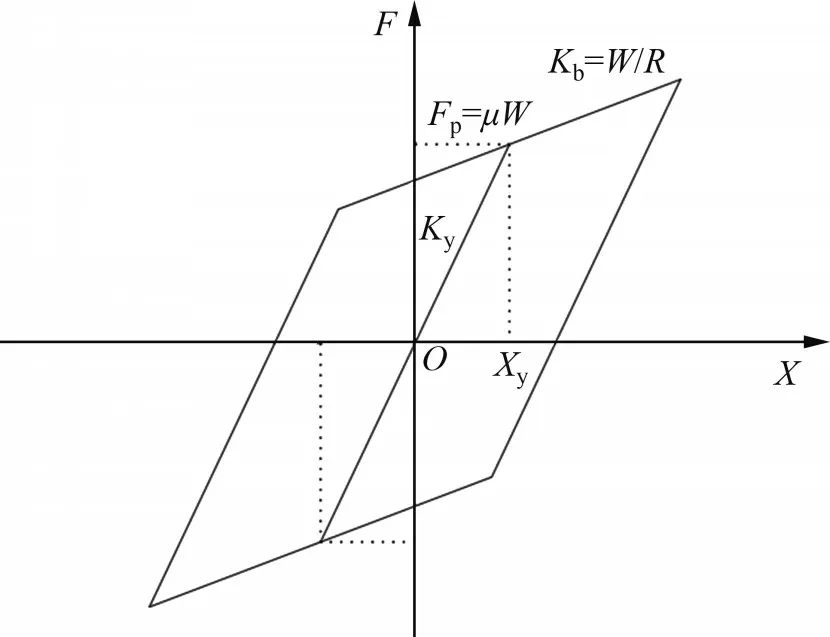
圖5 雙曲面球型減隔震支座力-位移關系Fig.5 Force-displacement relationship of hyperboloid spherical seismic isolation bearing

黏滯阻尼器的力學特性可由下式表征：

式中：Fd為阻尼力；C為阻尼系數，一般取值范圍為1 000～8 000 kN·s·m-1；v為墩梁間相對速度；sgn 為符號函數；α為速度阻尼指數，橋梁抗震工程中的常用取值范圍0.2～0.5。研究表明：剛構墩底彎矩隨阻尼系數C增大而減小，隨阻尼指數α減小而減小，但是阻尼系數過大時阻尼器出力多，導致阻尼器的安裝錨固較困難，阻尼指數過小則阻尼器加工困難。本文根據工程實際取阻尼系數C=4 000 kN·m2·s-2，速度阻尼指數α=0.3[16]。在CSiBridge 中，采用基于Maxwell 模型的damper 屬性單元進行模擬。

拉索減震支座由常規活動盆式橡膠支座和拉索組成。在拉索自由行程范圍內，不會影響梁體因溫度和收縮徐變而產生的變形，但在地震作用下，梁體較大變形會受到拉索的限制，同時使各橋墩協同抗震。支座力學特性按照圖6所示荷載-位移曲線進行模擬。圖6中，K1為活動盆式橡膠支座彈性剛度；Fs為滑動摩擦力，Fs=μFN，FN為豎向承載力；U0為拉索自由行程內允許的水平位移；K1為盆式支座屈前剛度；K2為拉索水平剛度。本文根據工程實際，拉索自由行程水平位移取為±10 cm，拉索提供的最大容許位移為±15 cm[17]。在5號墩設置3個拉索減震支座，每個支座共有10根拉索，每根拉索在地震作用下能承受的拉力為6 00 kN。在CSiBridge中盆式橡膠支座和拉索分別采用Plastic-Wen 連接單元和Multi-linear 連接單元模擬，而后再將兩者進行并聯模擬拉索減隔震支座。

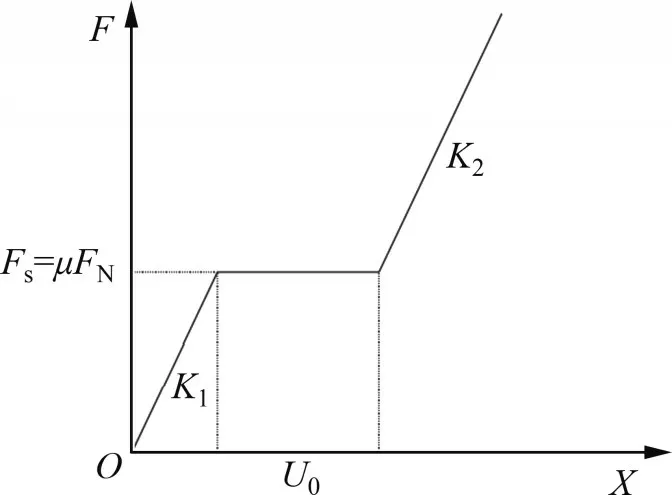
圖6 拉索支座計算模型Fig.6 Calculation model of cable

采用等效雙線性恢復力模型模擬高阻尼橡膠支座的滯回特性。在CSiBridge 中采用Rubber Isolator 非線性連接單元來模擬。選擇HDR(I)-d370×177-G1.0 型支座，水平屈服力為49 kN，初始水平剛度為6.62 kN/mm，屈后剛度為1.02 kN/mm。

4 橋墩截面分析

利用CSiBridge Section Designer 程序進行橋墩截面分析，定義材料本構關系并對各截面進行纖維單元劃分，輸入各橋墩在恒載下的軸力，通過迭代計算得到各截面的彎矩曲率曲線和等效雙折線模型。表1所示為等效雙折線模型中的特征參數。3 號墩墩截面配筋圖及其彎矩-曲率曲線分別如圖7 和圖8所示。空心薄壁矩形截面長×寬為840 cm×400 cm，縱橋向壁厚為70 cm，橫橋向壁厚為90 cm。3 號和6 號過渡墩是直徑為200 cm 的圓形截面，其余橋墩是直徑為130 cm的圓形截面。按照“公路橋梁抗震設計規范”中的公式計算各橋墩墩頂縱橋向允許位移，計算結果如表1所示。

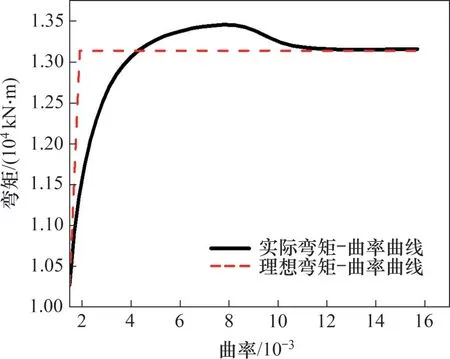
圖 8 4號墩截面M-?曲線Fig.8 M-? curve of pier No.4 section

表1 橋墩墩底截面特征參數Table 1 Section characteristic parameters value of pier bottom section

圖7 3號墩配筋截面Fig.7 Section of reinforcement for pier No.3

5 普通地震波作用下減震分析

在大跨度剛構-連續組合梁橋中各橋墩因約束不同，其內力分布不均，柔性剛構制動墩因具有較大內力和位移，導致伸縮縫碰撞力顯著增大。因此，減小剛構墩內力、變形和合理分配各橋墩水平地震力是剛構-連續組合梁橋減震設計的關鍵。本文由于兩主橋墩墩高相差較大，Lock-up速度鎖定裝置的使用受到限制，故采用黏滯阻尼器和減震支座進行減震措施研究[2]。本文通過在5 號墩、引橋墩和橋臺布置不同減震裝置來分析不同減震方案對橋臺-引橋-剛構連續梁橋結構體系減震效果的影響，具體減震方案如表2所示。

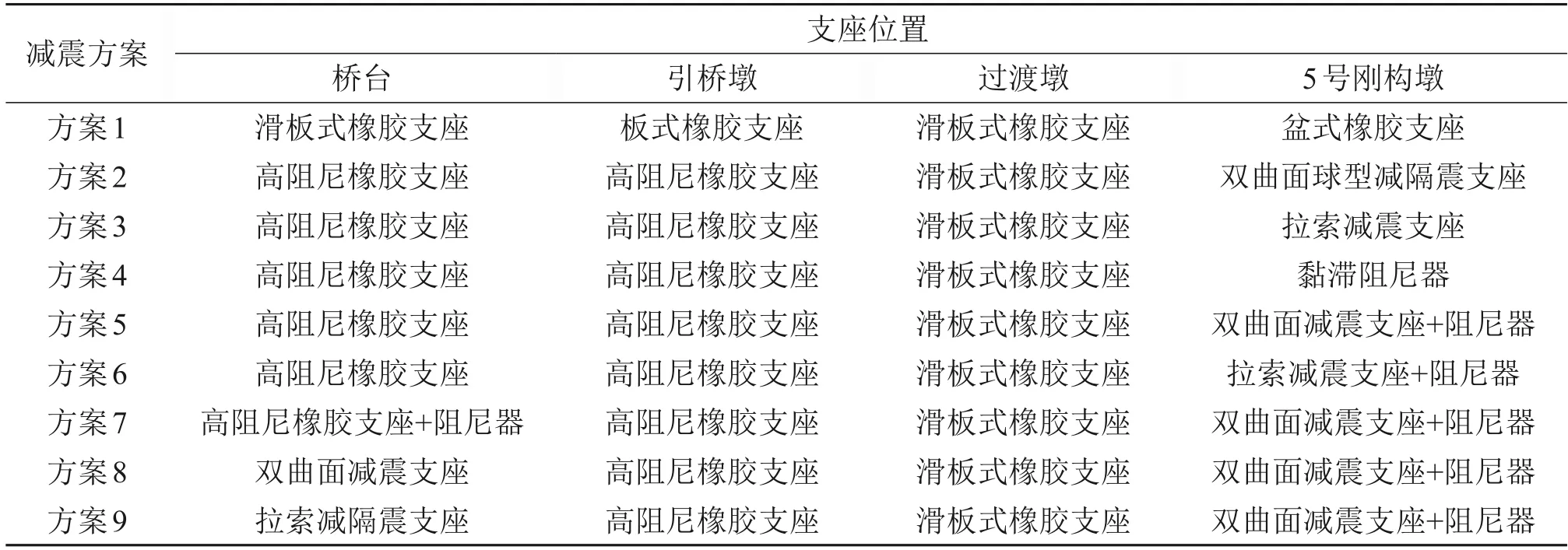
表2 普通地震波作用下減震設計工況Table 2 Design conditions of shock absorption under ordinary seismic waves

橋址處防烈度設為9度，場地類別為Ⅲ類，從PEER Ground Motion Database 強震數據庫中選擇場地條件相近的3 條地震波，取其平均值進行分析。利用SeismoMatch程序，以設計反應譜為目標對所選地震波進行調幅，得到與目標反應譜匹配的加速度時程。選取的3條地震波參數及其調幅信息分別如表3和圖9所示。本文采用縱橋向一致激勵非線性時程分析各方案的減震效果。

表3 選取的普通地震波資料Table 3 Selected ordinary seismic wave data

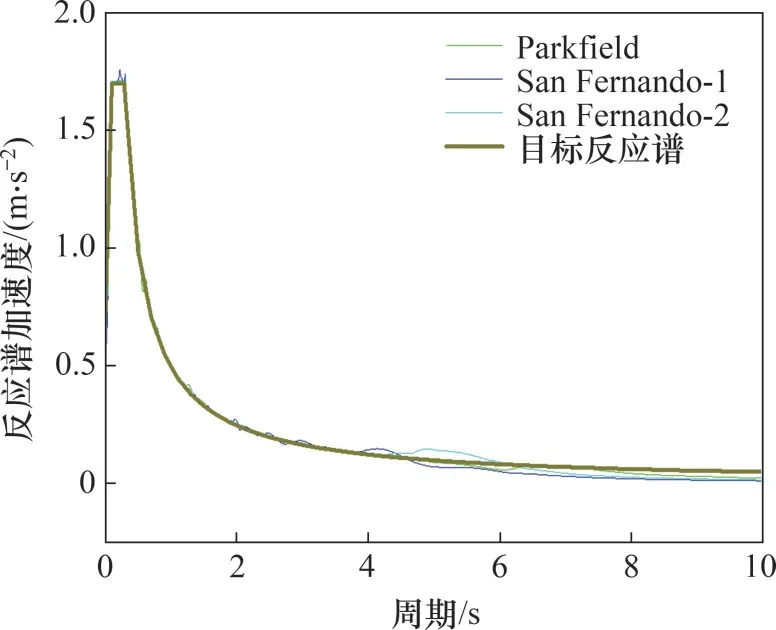
圖9 設計反應譜與天然波反應譜匹配圖Fig.9 Matching diagram of designed reaction spectrum and natural wave reaction spectrum

5.1 橋墩內力與變形分析

橋梁結構在不同減震方案下的墩頂位移和墩底彎矩分別如表4和表5所示。為量化說明各減隔震方案對結構地震響應的影響，本節定義變化幅度i=(imax-imin)/imin，其中imax為最大響應值，imin為最小響應值。各減隔震工況的共同趨勢如下：引橋墩頂位移增大，過渡墩頂位移和剛構墩頂位移減小，5號墩頂位移基本不變，達到了預期減隔震效果，但各方案減震效率存在差異。

表4 普通地震波作用下各橋墩墩頂位移Table 4 Displacement of pier top of each pier under ordinary seismic wave m

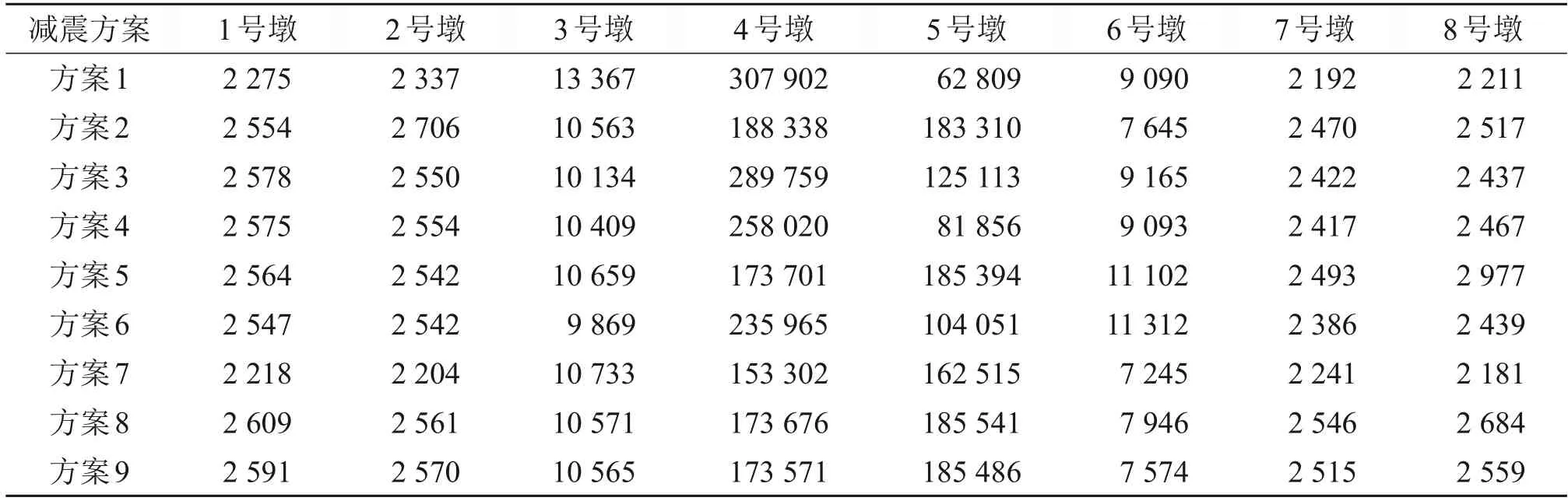
表5 普通地震波作用下各橋墩墩底彎矩Table 5 Bending moment at the bottom of each pier under ordinary seismic wave kN·m

方案2～4的減震方案分別是在5號墩設置雙曲面球型摩擦擺支座、拉索減震支座和黏滯阻尼器。4 號剛構墩墩頂位移從方案1 時的0.21 m 分別減小至方案2～4 時的0.11，0.20 和0.16 m，變化幅度分別為-47.6%，-4.8%和-23.8%；墩底彎矩從方案1時的307 902 kN·m 分別減小至方案2～4 時的188 338，28 9759 和258 020 kN·m，彎矩變化幅度分別為-38.8%，-5.9%和-16.2%。5號墩底彎矩由方案1 時的62 809 kN·m 分別增加至方案2～4 時的183 310，125 113 和81 856 kN·m。與方案1 相比，左右引橋墩墩頂位移和墩底彎矩在方案2～4中均呈現增大趨勢，最大變化幅度分別為133.3%和15.8%；除方案3 中的7 號墩外，其余引橋墩墩頂位移均已超過墩頂允許位移，但各橋墩墩底彎矩均未達到開始屈服彎矩。與方案1 相比，方案2～4中3 號過渡墩墩頂位移和墩底彎矩均呈減小趨勢，最大變化幅度分別為-54.6%和-21.0%；6 號過渡墩墩頂位移和墩底彎矩分別呈減小和略微增大趨勢，最大變化幅度分別為-50.0%和6.1%，過渡墩的墩頂位移和墩底彎矩均在安全值以內。通過分析主橋4號和5號橋墩的墩頂位移和墩底彎矩變化可以發現：使用單一減隔震裝置進行減震分析時，方案2中雙曲面球型摩擦擺支座具有更好的減震效果，但引橋墩墩頂位移超過允許范圍。

方案5 和方案6 分別是在方案2 和方案3 的基礎上再添加黏滯阻尼器進行組合減震。4號剛構墩墩頂位移由方案1時的0.21 m分別減小至方案5和方案6時的0.09和0.15 m，位移變化幅度為-57.1%和-28.6%；墩底彎矩由方案1 時的307 902 kN·m分別減小至方案5 和方案6 時的173 701 kN·m 和235 965 kN·m，彎矩變化幅度為-43.6%和-23.4%。5號墩底彎矩由方案1時的62 809 kN·m分別增大至方案5和方案6時的185 394 kN·m和104 051 kN·m，彎矩變化幅度為195.2%和65.7%。因此，采用方案5和方案6的組合減震方案可使剛構頂位移和墩底彎矩相對于采用單一減震方案時進一步減小，而5 號墩底彎矩并未顯著增大且遠小于屈服極限；但引橋墩頂位移相比方案2 和方案3 時進一步增大，超出墩頂允許位移。

方案7～9是在方案5基礎上將橋臺處支座分別更換為高阻尼橡膠支座+阻尼器、雙曲面球型摩擦擺支座和拉索減震支座的橋臺橋墩聯合減震方案。各減震方案左右引橋位移見圖10。將圖10以及表4和表5 中方案7～9 的結果與方案5 的結果進行對比可以發現：僅在橋臺處安裝黏滯阻尼器時，左右引橋位移、引橋墩頂位移和各橋墩墩底彎矩均呈現明顯減小趨勢，且各引橋墩頂位移均未超過允許值，而在橋臺處設置雙曲面球型減震支座和拉索減震支座對各橋墩內力和變形均未產生有利影響。

圖10 各減震方案左右引橋位移Fig.10 Left and right approach bridge displacements of various shock absorption schemes

5.2 伸縮縫碰撞效應分析

圖11所示為9 種方案中各伸縮縫處碰撞力峰值，由圖11 可以發現：各減隔震方案對于主引橋間伸縮縫B-C和C-D處碰撞效應的抑制作用明顯，B-C縫在采取減隔震措施后均未發生碰撞，C-D縫處僅在工況3、工況4 和工況6 中發生碰撞，碰撞力峰值和碰撞次數最小變化幅度分別為-19.8%和-50%。但是，橋臺處A-B和D-E伸縮縫的碰撞效應反而呈現增大趨勢，僅方案7中的伸縮縫碰撞力和碰撞次數顯著減小，起到了抑制碰撞的效果。因此，各減震方案均能減小主引橋間碰撞效應，但只有方案7才能減小橋臺處伸縮縫碰撞效應。

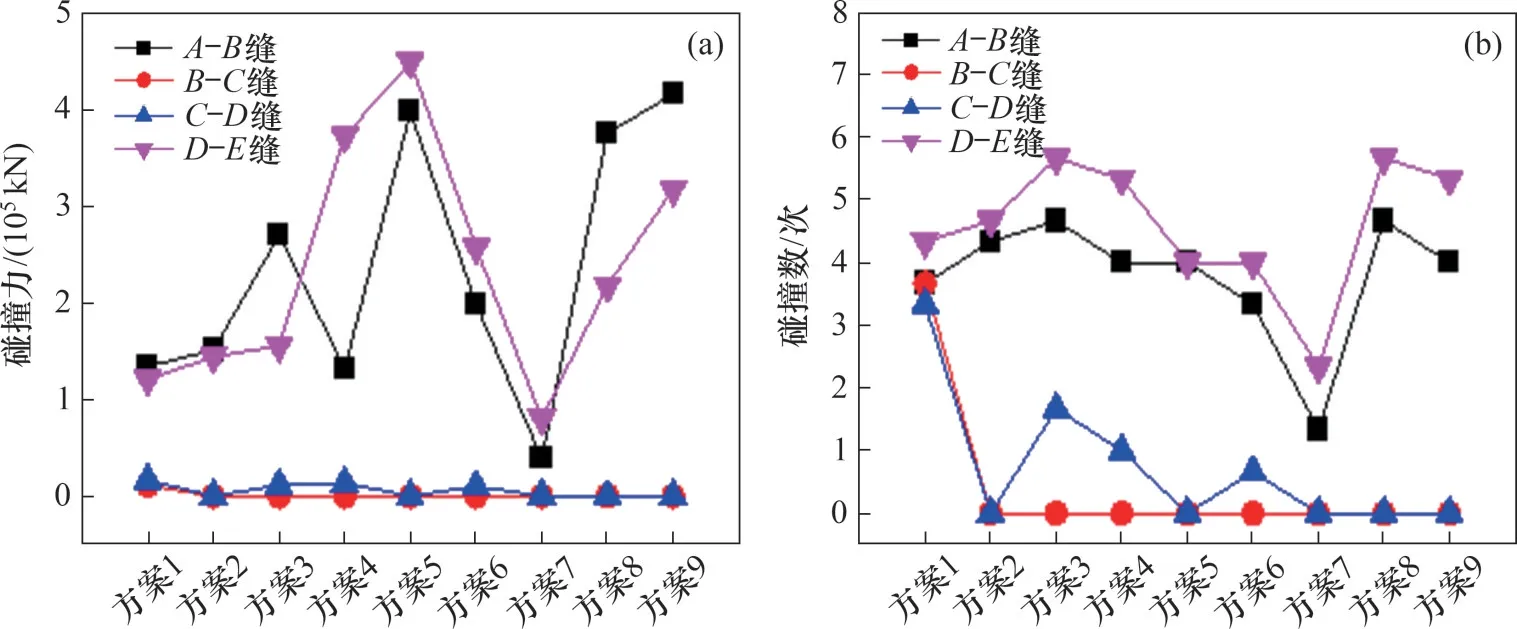
圖11 各減震方案伸縮縫處碰撞效應Fig.11 Collision effect at expansion joints of various damping schemes

因此，在普通地震波作用下既能使各橋墩內力合理分配且小于墩底截面屈服極限，同時還能使各伸縮縫處碰撞效應減小的減隔震方案為方案7，即在5 號墩頂布置雙曲面球型摩擦擺支座和黏滯阻尼器，同時在左右橋臺布置黏滯阻尼器。

6 近斷層脈沖型地震波作用下減震分析

研究表明[18-19]，減隔震結構在近斷層脈沖型地震波作用下的響應與普通地震波作用下的結構響應有明顯區別。下面分析在普通地震波作用下行之有效的減震方案是否在近斷層脈沖地震波作用下同樣具有較好的減震效果。同時，根據分析結果對減隔裝置參數進行調整和優化。

通過計算分析發現在脈沖型地震波作用下，剛構墩會發生顯著塑性變形，同時左右橋臺樁基也會發生屈服破壞。因此，在左右橋臺處布置滑板式橡膠支座，引橋墩頂布置高阻尼橡膠支座，使引橋墩承擔更多水平地震力。其他橋墩處的減震方案布置與近斷層普通地震波作用下的減震方案布置一致(見表2中方案1～6)。選擇Chi-Chi地震中的3 條近斷層脈沖型地震波進行縱橋向一致激勵，地震波參數如表6所示。

表6 近斷層脈沖型地震波參數Table 6 Parameters of near-fault pulsed seismic waves

6.1 橋墩內力與變形分析

近斷層脈沖型地震波作用下橋梁結構在不同減震方案下的墩頂位移和墩底彎矩分別如表7和表8所示。方案1 未采取減隔震措施，以方案1 中結構地震響應值為參考，分析長周期地震動作用下各減隔震方案的減隔震效果。

從表7和表8可以看出：在近斷層脈沖型地震波作用下，左右橋臺位移在各減震方案下顯著減小，均在0.1 m范圍內，最大變化幅度分別為-76%和-77%；各引橋墩頂位移增大且超出允許值；墩底彎矩增大且大于開始屈服彎矩，但小于等效屈服彎矩和極限屈服彎矩；各減震方案對于主橋墩的減隔震效果并不理想，方案3 和方案6 中，4 號和5 號墩底彎矩均超過屈服極限。方案2 和方案5中，雖然4號墩底彎矩減小，但5號墩底彎矩超過屈服極限；方案4中，4號墩底彎矩超過屈服極限。因此，在普通地震波作用下有效的5種減震方案在近斷層脈沖型地震波作用下對于主橋墩的減震效果均未能達到預期，需要對現有減震方案中的減震裝置參數進行優化。

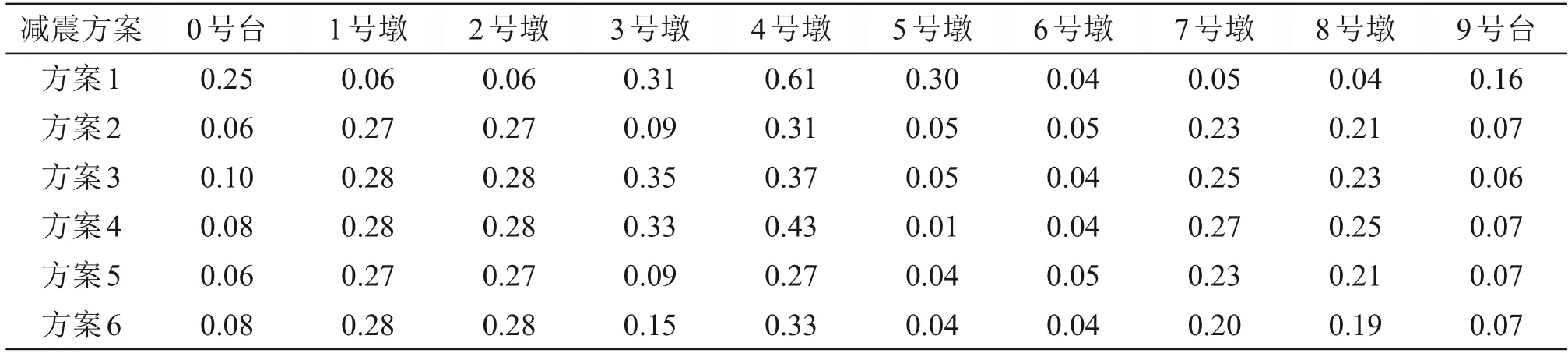
表7 近斷層脈沖地震波作用下各橋墩墩頂位移Table 7 The pier top displacement of each pier under near-fault pulse seismic wave m

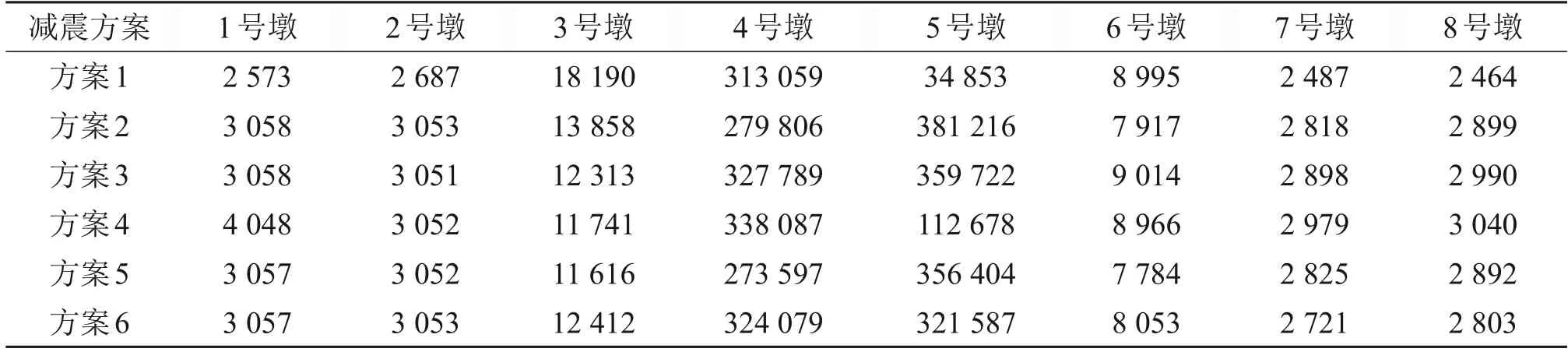
表8 近斷層脈沖地震波作用下各橋墩墩底彎矩Table 8 The bending moments at the bottom of each pier under near-fault pulse seismic waves kN·m

6.2 減震裝置參數優化

經綜合分析可知，雙曲面球型摩擦擺支座無論在普通地震波作用下還是在近斷層脈沖型地震波作用下均具有較好的減震效果。因此，本文僅以雙曲面球型摩擦擺支座為例進行參數優化，球心距R根據工程實際取0.5，1.0，2.0 和4.0 m；摩擦因數取0.02，0.04，0.06，0.08，0.10，0.12，0.14和0.16，將其兩兩組合進行參數分析，結果如圖12所示。

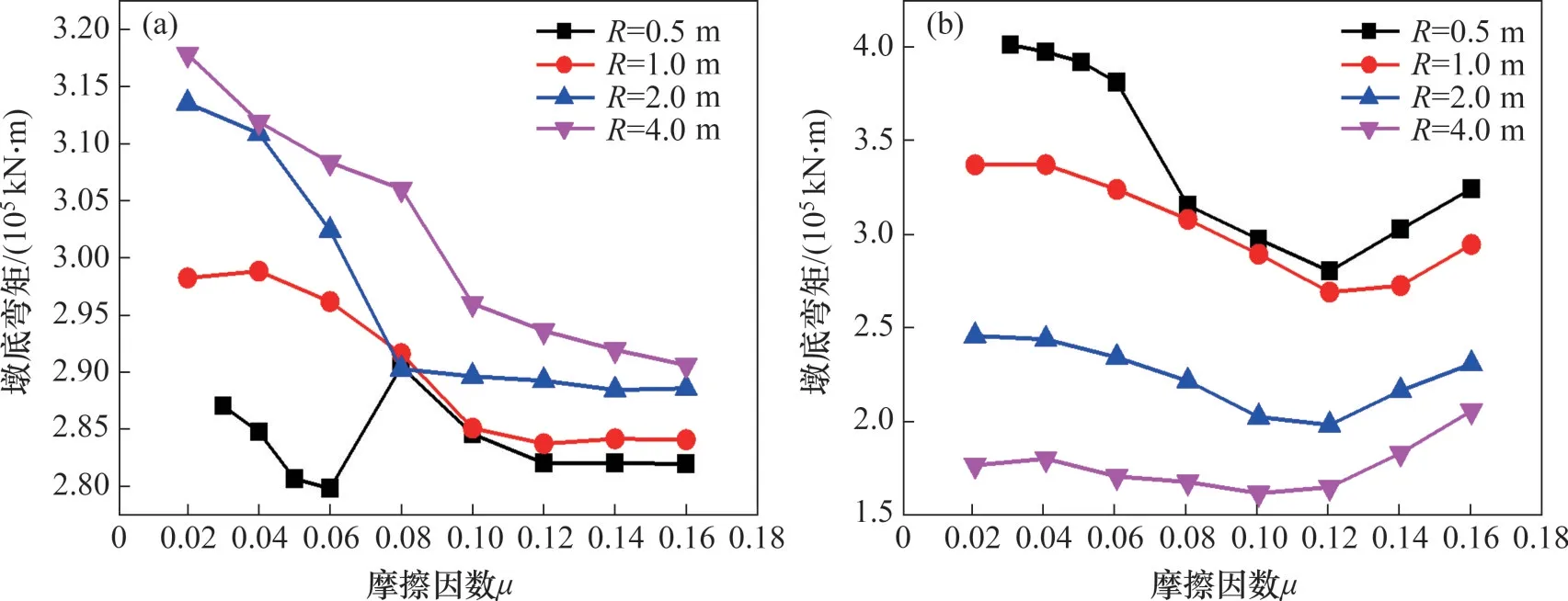
圖12 不同支座參數時的主橋墩底彎矩Fig.12 Bending moment at the bottom of main bridge pier with different support parameters

圖12(a)中，4號墩底彎矩隨摩擦因數μ的增大而減小，隨雙曲面球型摩擦擺支座球心距R的增大而增大，4 號墩底等效屈服彎矩為306 111 kN·m。由圖12(b)可以看出，5號墩底彎矩隨摩擦因數μ的增大呈先減小后增大趨勢，在μ=0.12 時5 號墩底彎矩最小(R=4.0 m 時除外)；同時，墩底彎矩隨球心距R的增大呈減小趨勢。當雙曲面球型摩擦擺支座球心距R=4.0 m，摩擦因數μ=0.10時，5號墩墩底彎矩最小。但為了使主橋墩墩底彎矩均達到最優受力狀態，本文建議采用球心距R=2.0 m、摩擦因數μ=0.10的支座，此時，成本較低，且4號和5號墩均能達到較好的受力狀態。

7 結論

1)在普通地震波作用下，不同減震方案均能使各橋墩內力達到預期的減震效果。采用單一減震裝置時，在5 號墩采取雙曲面球型減震支座最佳，采取減震支座加黏滯阻尼器的組合減震方案的減震效果比采用單一減震支座方案的減震效果更好，但進一步增大了引橋墩頂位移。

2)各減震方案均能減小主引橋間碰撞效應，但橋臺處伸縮縫碰撞效應僅在橋臺處設置黏滯阻尼器后顯著減小，因此，采用方案7中的橋墩和橋臺聯合減震方案才能使橋梁結構體系的內力和碰撞效應均得到有效控制，同時也使各引橋墩頂位移小于允許值。

3)在普通地震波作用下有效的減震方案在近斷層脈沖型地震波作用下均不能達到預期減震效果。但是，對減震裝置參數進行適當優化后仍然可以減小主橋墩內力和位移，達到預期減震效果。