考慮間斷級配的破碎矸石壓實和再破碎研究

張天軍，王小軍，龐明坤，張碩，王飛

(1.西安科技大學 安全科學與工程學院，陜西 西安，710054；2.西安科技大學 理學院，陜西 西安，710054；3.陜西彬長文家坡礦業有限公司，陜西 彬州，713504)

充填材料的壓實和再破碎特征是影響采空區充填效果和質量的重要因素，采空區的充填效果控制著上覆巖層移動與地表沉降[1-3]。矸石作為一種散體材料[4]，其級配是影響矸石壓實特性的重要因素。采礦過程的破碎矸石、摻礫黏土等均處在一種間斷級配狀態[5-7]。間斷級配是指缺少某一個(或幾個)粒徑區間顆粒而構成的一種級配[8]。關于連續級配巖石顆粒，郁邦永等[9-11]發現，級配顆粒的冪指數越大，被壓碎的巖石顆粒越多；張吉雄[12]得到了應變、壓實度與應力的關系；張德輝等[13]發現連續級配煤矸石的壓縮率與軸壓、側壓曲線近似滿足指數關系；馬占國等[14]通過試驗得到了軸向應變、橫向應變、泊松比、彈性模量等參數的變化規律；張天軍等[15-16]發現隨著環境濕度增大，承載能力下降，級配指數越大，則破碎率變化幅度越大。

對于間斷級配巖石顆粒的研究目前大多集中在滲透不穩定性方面[17-19]。ⅤENUDHARAN等[20]發現當混合料中粗細顆粒配比合理時，可以提高級配結構的抗壓強度。OLARD[21]認為減少中間顆粒的數量，降低細顆粒平均粒徑與粗顆粒平均粒徑的比值可以減小混合料的孔隙率，并將該理念應用于路面瀝青混凝土的設計中；張冬梅等[22]針對間斷級配砂土中管線破損引起周圍土體的滲流侵蝕等問題，分析了地下空洞產生的原因及顆粒流失的發展規律；楊陽等[23]利用侵蝕柱體在溶解過程中侵蝕管涌通路，發現隨著侵蝕過程加劇，砂土的剪切波速逐漸降低，且降低幅度隨圍壓和密實度的增大而增加；劉國耘[24]認為以連續級配的集料為骨架，并用連續級配的細集料填充間斷級配料的孔隙，可以形成一個高密度結構。

學者們對間斷級配顆粒的研究多是基于滲透不穩定性方面的試驗研究，對級配散體顆粒側限壓實和再破碎特征之間的內在機理分析較少。本文針對連續級配及間斷級配的破碎顆粒矸石，采用分級加載方式進行側限單軸壓縮試驗，研究級配破碎矸石的壓實及其再破碎特征；依據實驗結果并結合前人研究成果，利用極限法求出極限位移和極限壓實度，通過消參法分別建立壓實度增量和分形維數、應變和分形維數增量之間的數學模型，并以極限法確定公式中參數的物理意義，據此探討側限壓實和再破碎之間的內在關系。

1 破碎顆粒壓實變形再破碎過程

對于單一粒徑巖石破碎體而言，其破壞類型主要分為破裂、破碎和研磨3種，破壞后變為更小的橢球狀或粉末狀顆粒，如圖1所示。

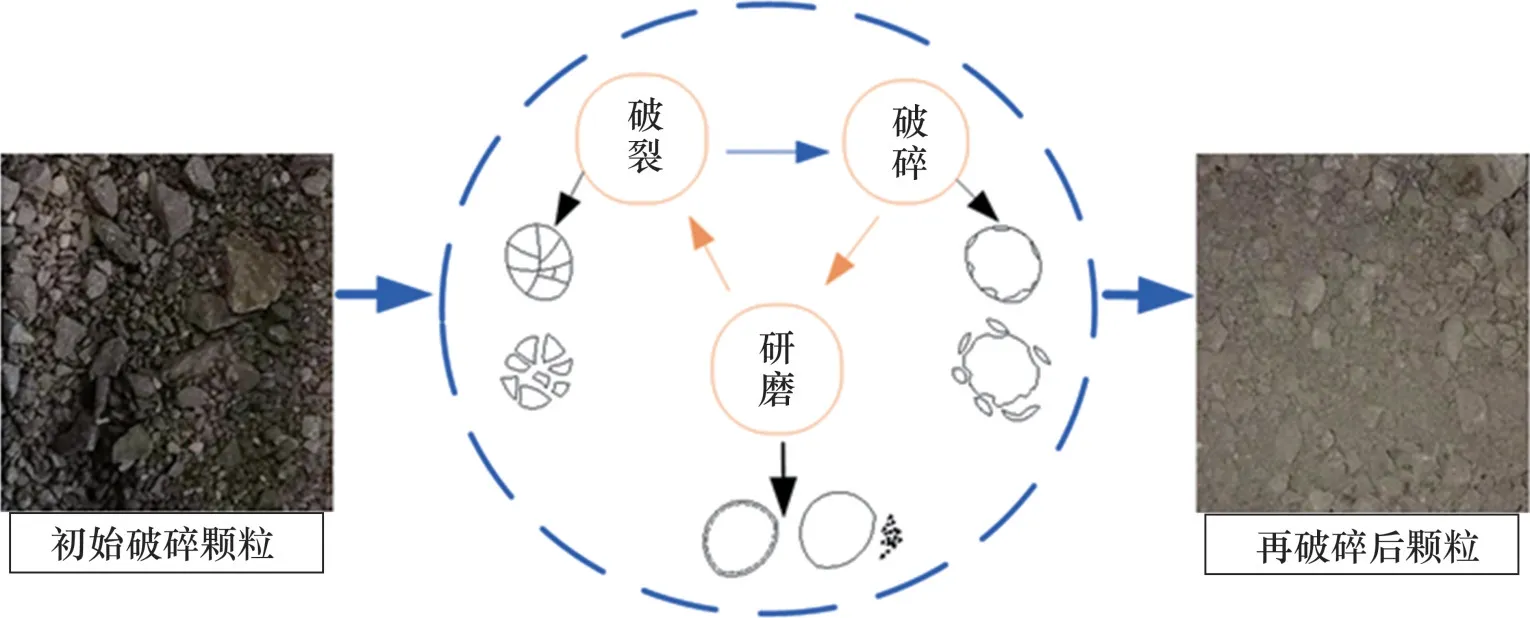
圖1 顆粒破碎模式Fig.1 Particle breakage pattern

初始狀態的破碎巖石顆粒基本呈棱臺狀或者錐形狀，且棱角分明，其形狀特征明顯且多元化。對于骨架結構棱角較為尖銳的錐形狀，在承壓過程中，顆粒之間發生點接觸并造成應力集中，最終導致顆粒棱角的脫落，脫落后的細小顆粒填充到大顆粒之間的空隙中。對于棱臺狀顆粒，在外載荷作用下發生破裂變為較小的顆粒，骨架的破壞使得外載荷直接作用在較小的破碎顆粒上，造成缸筒內巖石顆粒的空隙減小，破碎巖石顆粒之間變得更為密實。此時，較小顆粒相對于細小顆粒而言承擔了骨架角色，在外載荷不斷作用下，破碎顆粒不斷發生破裂、破碎、研磨一系列復雜的變化，使大顆粒變成橢球狀或粉末狀。因而，在缸筒內對破碎巖石顆粒進行承壓壓實試驗時，發生二次破碎，破碎的主要形式為骨架的破壞和非骨架中細小顆粒的研磨破碎。

從破碎巖石顆粒組成的宏觀系統來看，破碎巖石顆粒在缸筒中進行壓縮試驗過程中，主要表現為整個破碎巖石試樣軸向位移和體積的變化，如圖2所示。圖2中，h0為試樣初始高度，h為承壓過程中試樣高度，hlim為完全壓實后試樣高度。

圖2 破碎巖體壓實過程Fig.2 Compaction processes of fractured rock mass

在載荷作用下，一定質量的破碎巖石顆粒主要表現為試樣軸向位移增大，體積不斷減小。在顆粒填充下破碎試樣中較大的間隙填充基本完成，無法再通過顆粒間的移動來減少空隙，此時，在較大的軸向應力下巖石顆粒發生破碎、破裂、研磨等，使大顆粒變成較小顆粒填充到剩余的空隙中，從而減小破碎煤巖體的空隙，使其進一步壓實。當顆粒間的孔隙小到一定程度時，破碎煤巖體在高應力的作用下發生固結、黏結等效應，使級配破碎巖石顆粒被壓實成為接近原巖體的類原巖體。空隙的不斷減小以及骨架占比不斷增大，導致級配巖石顆粒的骨架作用不斷增強。因而，該過程也是一個級配破碎巖石顆粒抗壓縮能力不斷增大的過程。

2 試驗方法

2.1 試驗設備

采用DDL600破碎巖石壓縮系統進行試驗，它是一種多功能巖石力學試驗系統，該系統主要用于開展滲流、剪切、單軸壓縮等試驗。該系統主要包括電子萬能試驗機DDL600、壓實裝置、電子分析天平和主控計算機等，如圖3(a)所示。其中，破碎巖石壓縮裝置主要由缸筒、活塞、毛氈等組成，缸筒高度與內徑分別為200 mm和100 mm。考慮到試樣在受載過程中的徑向應變和環形應變會對試驗精度產生影響[10]，因而，試驗所用缸筒采用剛度較大的鈦合金材料，以盡可能提高試驗精度。試驗前在缸筒內壁及活塞上涂抹潤滑油，在后續試驗中忽略缸筒與試樣接觸的摩擦阻力的影響。試樣底部裝有毛氈，以防止煤矸石樣顆粒從底部通口處流出，避免矸石顆粒質量流失對實驗結果產生影響。

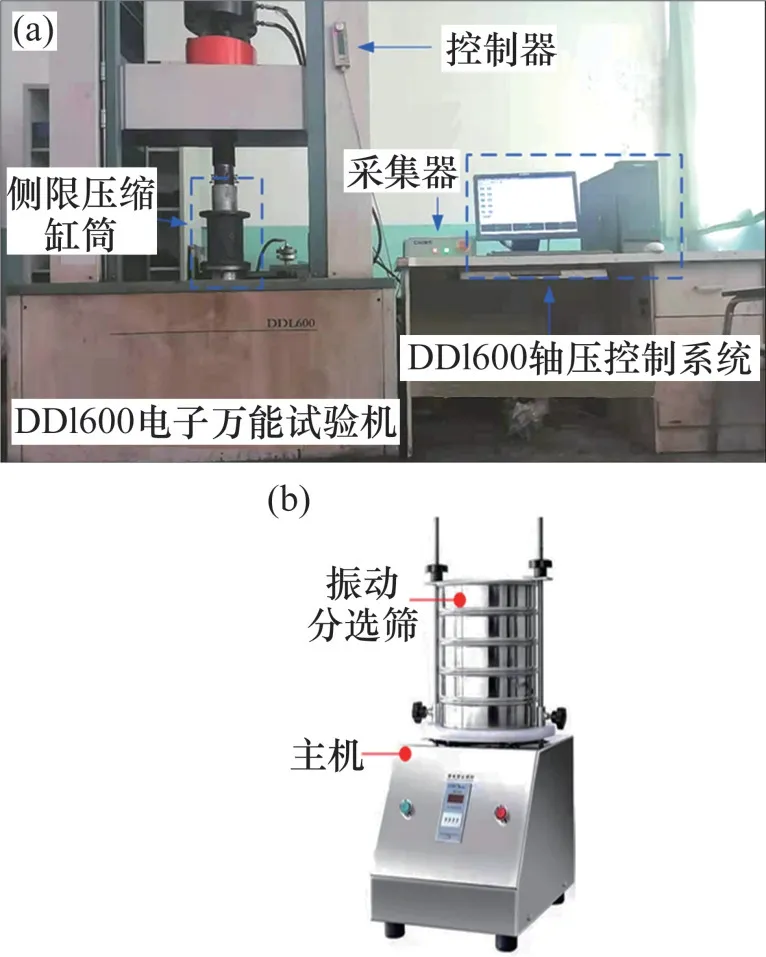
圖3 破碎巖體壓縮試驗設備Fig.3 Crushed rock compression test equipment

2.2 試驗原理與步驟

分形維數是表征破碎顆粒粒度分形復雜程度的參數。根據分形維數的基本表達式[10]，飽和破碎巖石顆粒數量與粒徑的關系可表示為

式中：x為級配特征粒徑即篩孔孔徑；d為破碎煤巖顆粒的粒徑；N為破碎顆粒的直徑小于等于d的破碎顆粒數量；C為特征常數；D為分形維數。根據破碎煤巖體的顆粒質量M與特征尺度的關系，M∝d3，破碎顆粒中粒徑小于d的顆粒質量Md可以表示為

式中：λ為破碎煤巖顆粒的形狀系數；ρ為巖石顆粒密度；dmin為破碎顆粒的最小粒徑。將式(1)代入式(2)，記破碎煤巖體的最大顆粒粒徑為dmax，則破碎煤巖體顆粒的總質量Mt表達式為

根據式(3)可得到破碎顆粒中的粒徑小于d的顆粒質量Md與試樣整體總質量Mt的比值，其表達式如下：

破碎煤巖體在軸向應力作用下，顆粒之間會發生研磨并產生一些粉末狀的顆粒，與破碎試樣顆粒中最大粒徑的顆粒相比，最小粒徑dmin可定義為0 mm，則式(4)可以進一步表示為

對式(5)兩邊同時取對數可得：

本次破碎煤矸石加載試驗通過破碎巖石篩分裝置選取顆粒粒徑分別為(0～5]，(5～10]，(10～15]，(15～20]，(20，25]mm 的5 組煤矸石原料。根據連續級配理論，取冪指數n=0.2，0.4，0.6 和0.8，在不同n下均配制3組試樣，1組為連續級配試樣，其余2組為間斷級配試樣，每組試樣采用4級應力分級加載，應力分別為2，4，8和12 MPa。每組試樣質量為1 000 g。將每組試樣分別裝入不同的容器盒，并進行編號。加載方式設置為應力加載，加載速度設置為0.05 MPa/s。為使試樣充分變形和破碎，試樣加載到某一級應力后，應力保持時間設置為30 min。為避免人工篩分所引起的誤差，采用破碎煤巖體自動篩分裝置篩分得到再破碎后煤矸石的不同粒徑區間顆粒。根據試驗所選篩網，按照顆粒粒徑，依次在自動篩分裝置上安裝好相應顆粒粒徑的篩網，并將篩網固定，如圖3(b)所示。然后，在最上層裝入破碎矸石顆粒，然后開啟電源開關，運行5 min即可保證顆粒被充分篩分。

2.3 試樣配制

連續級配曲線和間斷級配曲線示意圖如圖4所示，以連續級配為基準，間斷級配曲線可以看作是在基準級配上剔除某一粒徑區間顆粒所形成的級配曲線。其中，w為細料質量分數；di為間斷粒徑區間中顆粒粒徑最小值，mm，dj為間斷粒徑區間中顆粒粒徑最大值，mm。

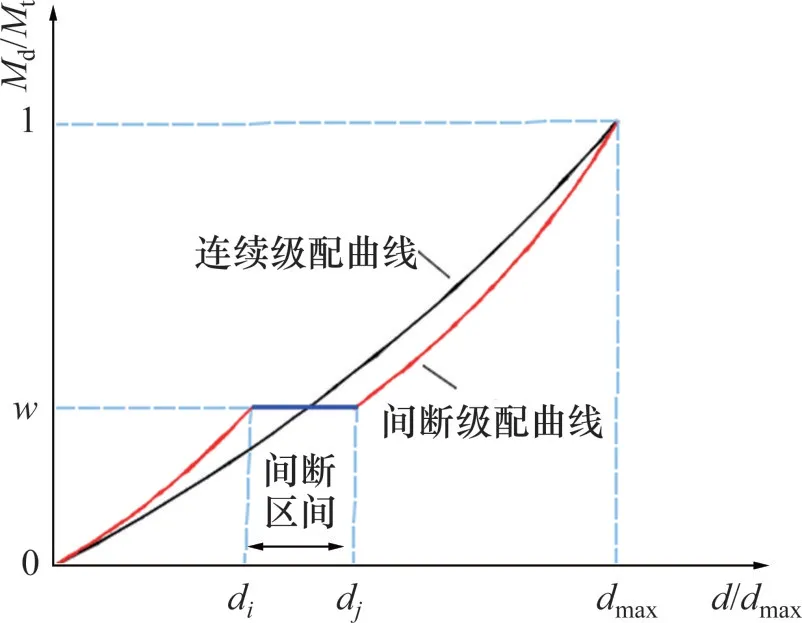
圖4 級配曲線示意圖Fig.4 Diagram of gradation curve

為后續繪圖和分析方便，下文中出現的間斷區間di～dj是指級配中缺失矸石顆粒粒徑d大于di而小于等于dj。例如，間斷區間0～5 mm，即指級配中缺失粒徑大于0而小于等于5 mm顆粒所構成的級配。

采用連續級配理論配置不同冪指數n下連續級配試樣，根據Talbot 級配公式[9]計算總質量為1 000 g的各粒徑區間質量。

連續級配下破碎矸石顆粒質量分布如表1所示。

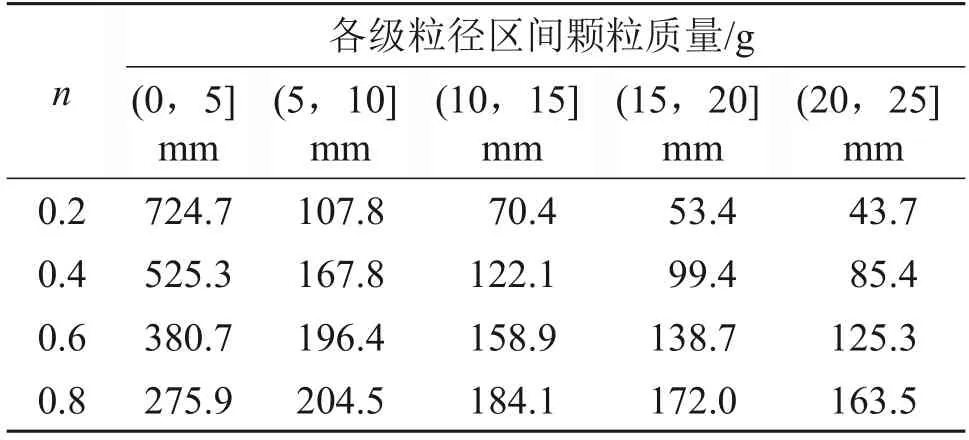
表1 連續級配顆粒質量分布Table 1 Mass distribution of continuous gradation particle

間斷級配試樣與連續級配試樣質量相同，基于等比放大原則，每個冪指數n下設置間斷0～5 mm粒徑顆粒和間斷15～20 mm粒徑顆粒兩種級配結構。本文定義粒徑在0～5 mm范圍內的顆粒為細粒，粒徑的顆粒大于5 mm為粗粒。設細料質量為Ms，粗料質量為Ml，則細料質量分數w可以由下式確定：

間斷級配下各粒徑區間顆粒質量分布如表2所示。

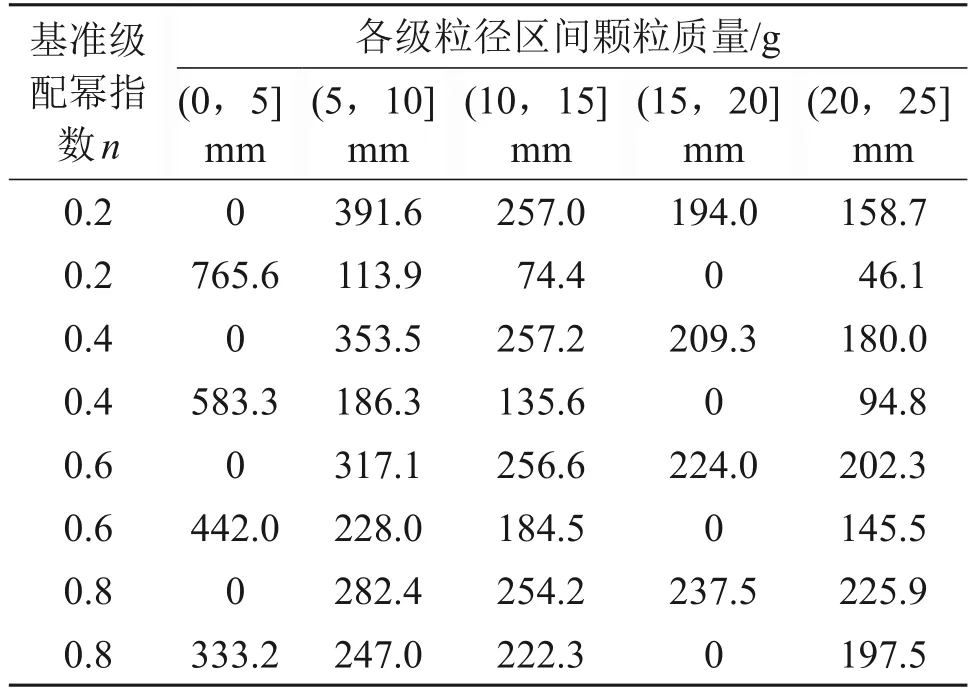
表2 間斷級配顆粒質量分布Table 2 Mass distribution of missing gradation particles

3 級配破碎矸石變形壓實特性

3.1 軸向位移-軸向應力曲線

軸向位移s可通過計算試樣各級應力作用下的高度h和初始試樣高度h0之間的差值求得：

破碎矸石在帶側限的缸筒中受側向約束，因為缸筒剛度較大，其徑向變形可以忽略不計，所以只產生軸向應變。軸向應變ε是指任一級軸向應力作用下，軸向位移和試樣初始高度的比值：

郁邦永等[10]通過實驗發現連續級配破碎巖樣軸向位移s與軸向應力σ之間滿足負指數函數關系：

式中：a1和b1均為擬合參數。對式(11)兩邊同時除以h0后即可得到應變和應力的關系：

對式(12)求導即可得到壓縮模量ES：

從式(13)可以看出，當軸向位移s趨于a1時，壓縮模量趨于無窮大，這表明a1即為極限位移。

根據試驗結果，繪制不同級配破碎矸石的軸向位移-軸向應力曲線，見圖5。由于擬合結果中b1是一個負值，對式(11)中的軸向應力取極限值，即可得到極限位移slim：

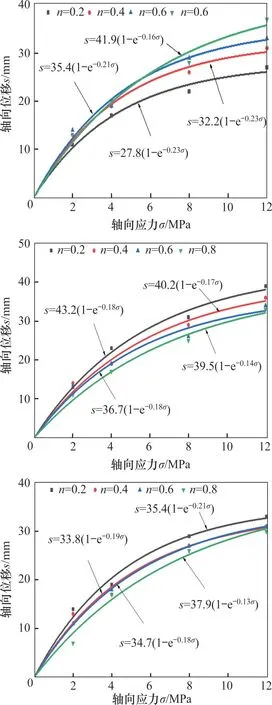
圖5 試樣軸向位移-軸向應力曲線Fig.5 Axial displacement-axial stress curve of samples

從式(14)可以得知軸向位移隨軸向應力變化呈現出收斂特性，b1越小，則收斂速度越快，即相應級配軸向位移隨應力變化趨于穩定的速率更快。

從圖5可看出，軸向位移與軸向應力符合指數函數關系，且相關系數在98%以上，表明式(11)對連續級配和間斷級配試樣均適用。隨軸向應力增加，軸向位移呈增加趨勢。當應力為0～4 MPa 時，位移處于快速增加階段，當應力大于4 MPa時，位移處于緩慢增加階段；大約60%的位移增量發生在快速增加階段。對于連續級配試樣，冪指數n越大，極限位移越大。對比圖5(a)和(b)可知，間斷0～5 mm粒徑級配試樣整體位移較大。這是因為主導位移增量的主要階段是快速變形階段，破碎矸石壓實過程中位移的變化主要是以移位重組填補空隙為主，大粒徑顆粒質量越大，顆粒之間的初始空隙大，因而產生的變形大。

3.2 級配結構抗壓縮性能分析

當n=0.2 時，連續級配試樣在軸向應力σ分別為0，4和12 MPa下的顆粒壓實狀態實物圖見圖6。從圖6可以看到：破碎矸石在軸向應力作用下，顆粒棱角脫落，變得光滑，顆粒粒徑不斷減小。顆粒與顆粒之間由松散狀態逐漸變為密實狀態，顆粒與顆粒之間的嵌合程度隨之增強。

圖6 不同軸向應力下的矸石顆粒壓實狀態實物圖Fig.6 Physical diagrams of compaction state of gangue particles under different axial stresses

為考察壓縮模量的變化，根據式(13)繪制壓縮模量和軸向應力的曲線，如圖7所示。

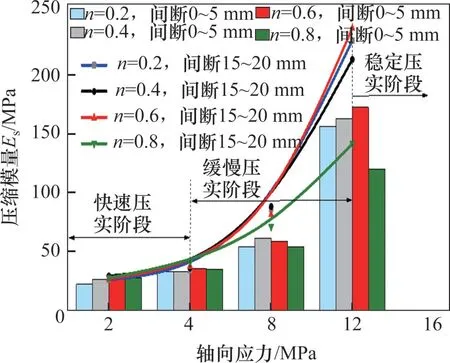
圖7 壓縮模量-軸向應力曲線Fig.7 Compression moduli-axial stress curve

從圖7可看出，當應力為0～4 MPa時壓縮模量小于50 MPa，壓縮模量隨軸向應力的變化呈緩慢增大趨勢，此階段試樣處于快速壓實階段，應力卸除后具有較強的彈性效應，壓縮模量隨軸向應力變化近似呈線性關系。在快速壓實階段，軸向應力所做的功主要用于克服顆粒與顆粒之間的摩擦力，且應力集中在空隙附近，當空隙附近的應力超過靜摩擦力，將引起空隙附近的局部失穩，即顆粒克服內摩擦力填充到空隙中或導致顆粒與顆粒之間的嵌合。

當應力為4～12 MPa 時，壓縮模量隨軸向應力的增大而快速增加，級配試樣抗壓縮能力顯著增強，此階段壓縮模量隨軸向應力的變化呈現出快速增大趨勢。試樣變形速度逐漸變緩，處于緩慢壓實階段。這是因為經過快速壓實階段，試樣內的空隙被壓縮及其內部結構調整優化，大顆粒的骨架作用不斷增強，承載骨架中的顆粒由于應力集中而產生大量破碎，破碎的小顆粒填充到空隙中，進一步減小了空隙，試樣承載能力大幅提升。此階段試樣變形表現為應變硬化特性，具有較強的塑性。在塑性變形階段散體顆粒壓縮模量與塑性應變之間呈顯著的非線性相關關系。

當應力大于12 MPa 后，壓縮模量整體上大于100 MPa，此階段試樣形成相對穩定的骨架承載結構，大顆粒被小顆粒緊密包圍，降低了壓實過程中應力集中效應，較大顆粒很難發生再破碎。因而，承載骨架發生失穩破壞的可能性較低，主要以結構微調、骨架優化為主。此階段級配試樣穩定性越來越強，處于穩定壓實階段，破碎矸石巖體成為接近原巖體的類原巖體。根據文獻[25]可知，當研磨小顆粒足夠多，使得大顆粒被小顆粒包圍而處于“懸浮”狀態時，可能會導致級配承載能力下降。

對于深部礦井精準充填，需要考慮高應力時的壓實情況。因此，采用極限位移分析不同級配的極限壓實度。壓實度可用來表征試樣在外力作用下的壓實程度：

式中：K為壓實度；V2為壓縮后的體積；V1為壓縮前的體積。由于缸筒底面積恒定，因而壓實度K可簡化為

由式(9)，(14)和(16)可推導出壓實度的極限值Klim為

為考察不同級配試樣的抗壓縮性，定義壓實度極限值大于0.7即高應力作用下變形不超過30%的級配試樣具有較強的抗壓縮性能。根據式(17)繪制出壓實度極限值Klim與Talbot指數n之間的關系，如圖8所示。

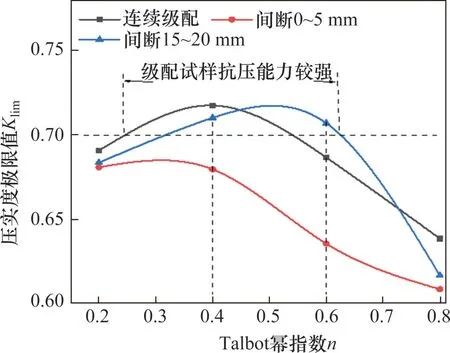
圖8 壓實度極限值-Talbot指數曲線Fig.8 Limit-Talbot exponential curve of compactness

由圖8 可知，間斷0～5 mm 級配試樣壓實度極限值Klim隨n增大而減小，連續級配和間斷15～20 mm級配試樣壓實度極限值隨n增大呈現出先增后減的趨勢。當n=0.4時，連續級配試樣具有最大極限壓實度，表明其抗壓縮性最強。當0.4＜n＜0.6時，間斷15～20 mm級配試樣壓實度極限值大于0.7且存在最大值，表明此階段級配試樣具有良好的抗壓縮性，結合表2 和式(8)，可知級配結構中0～5 mm 細顆粒質量分數為44.2%～58.3%。間斷0～5 mm粒徑級配結構壓實度極限值始終小于0.7，抗壓縮性最弱。這說明，對于壓實性而言，級配結構中缺失小粒徑顆粒比缺失中間粒徑顆粒的影響大得多，缺少中間粒徑的顆粒，顆粒級配結構的壓實度可能會提高，這與于際都等[25]的結論相符。

4 級配粒徑分布及其分形特征

4.1 粒徑區間分布

為研究破碎矸石壓實過程中缺失小粒徑和缺失中間粒徑顆粒對破碎矸石再破碎特征的影響，根據實驗結果繪制出間斷0～5 mm和間斷15～20 mm級配壓實過程中各個粒徑區間所含顆粒質量分數wp與軸向應力σ之間的關系，如圖9所示。

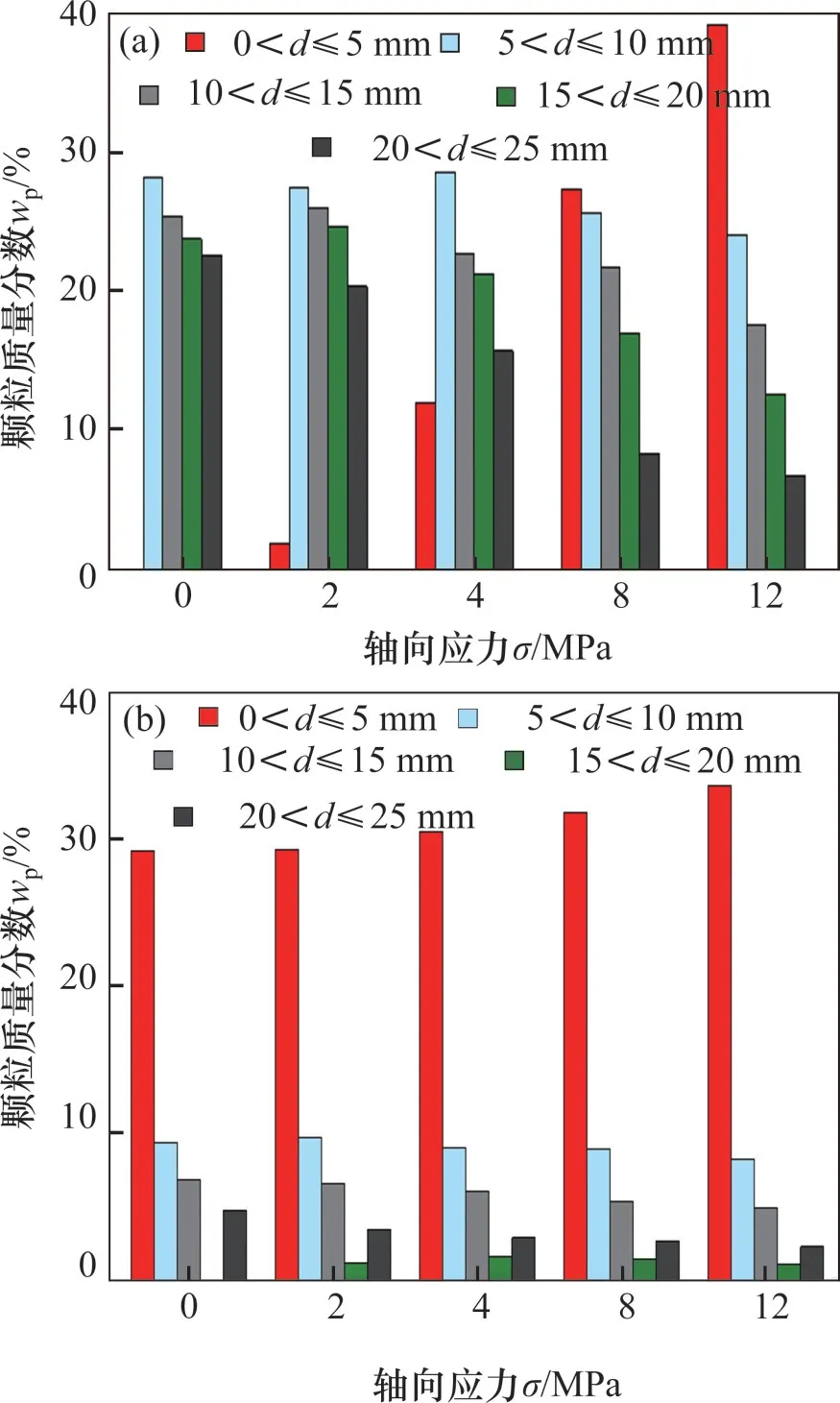
圖9 顆粒質量分數-軸向應力關系Fig.9 Relationship between particle mass fraction and axial stress

從圖9可看出，破碎矸石壓縮過程中主要表現為大粒徑顆粒質量分數不斷減少，小粒徑顆粒質量分數不斷增大。從顆粒粒徑遷移角度來講，隨軸向應力增大，大粒徑區間顆粒不斷發生破碎后遷移到小粒徑區間，初始間斷級配中間斷區間的顆粒得以補充。當0＜σ≤4 MPa 時，間斷0～5 mm 級配中0～5 mm 粒徑的小顆粒質量分數增加了11.9%；間斷15～20 mm的級配中0～5 mm粒徑的小顆粒質量分數增加了2.8%。當4＜σ≤12 MPa 時，間斷0～5 mm 的級配中0～5 mm 粒徑的小顆粒質量分數增加了27.4%；間斷15～20 mm的級配中0～5 mm的小顆粒質量分數增加了6.2%。即間斷0～5 mm 級配中0～5 mm小顆粒質量分數相較于間斷15～20 mm級配中0～5 mm小顆粒質量分數增加幅度大。這表明缺失小顆粒，級配更易發生再破碎，且試樣中顆粒的再破碎主要發生在緩慢壓實階段(4＜σ≤12 MPa)。

4.2 分形維數變化

依據式(6)可求得lg(Md/Mt)與lg(d/dmax)的關系，其斜率為3-D，從而可求得D。郁邦永等[9]通過實驗得到連續級配破碎樣分形維數與軸向應力之間的關系式：

式中：a2，b2和c2均為擬合參數。

為考察不同級配結構的試樣在不同軸壓下分形維數的變化情況，這里以n=0.2時的3組試樣結果為例，繪制分形維數D與軸向應力的關系，如圖10所示。由圖10 和式(18)可知，本文b2為負數，對式(18)中的軸向應力取極限值，則分形維數隨軸向應力變化趨于c2，b2越小，趨于c2的速度越快。

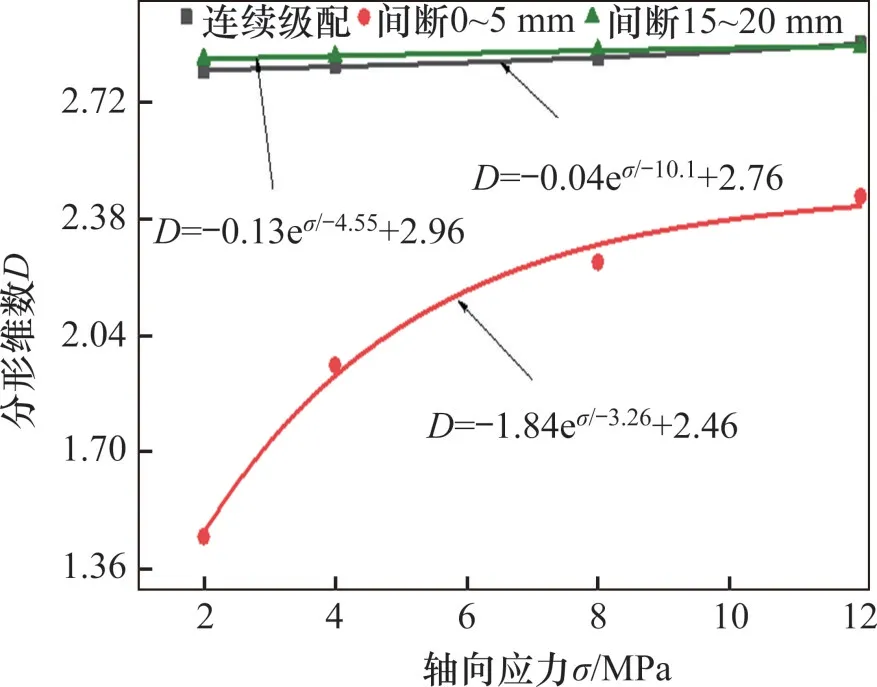
圖10 分形維數-軸向應力曲線Fig.10 Fractal dimension-axial stress curve

由圖10可以看出，式(18)擬合結果與實際結果一致性高，相關系數在99%以上。整體上，連續級配和間斷級配下試樣分形維數均隨軸向應力的增加而增加，這是由于不同級配試樣在壓縮過程中會發生大量顆粒破碎，使不同級配均向著某一最優級配進行演化。間斷0～5 mm級配結構的分形維數受軸向應力影響明顯，級配穩定性較差；間斷15～20 mm級配的粒徑顆粒的分形維數隨軸壓變化較為緩慢。此外，間斷0～5 mm級配試樣的分形維數始終小于其他2種級配試樣的分形維數，而隨應力的增加，間斷15～20 mm級配試樣的分形維數與連續級配試樣的分形維數趨于一致，兩者之間的差值越來越小。這表明級配中缺失小粒徑顆粒對分形維數的影響要比缺失中間粒徑顆粒的影響大。

5 壓實和再破碎模型及其參數物理意義

級配破碎煤矸石壓實和再破碎過程是一個相互作用的動態變化過程。隨軸向應力增加，破碎矸石構成的系統體積不斷減小，空隙隨之減小，破碎矸石不斷被壓實。從統計學角度來看，矸石顆粒發生再破碎，粒徑不斷減小，原本處于某一粒徑區間的破碎顆粒進行重新分布，因而破碎矸石顆粒的壓實過程也是一個顆粒再破碎和粒度分形演變過程，兩種動態變化過程必然存在某種潛在關系。

HARDIN[26]認為隨著軸向應力的增加，大粒徑顆粒會完全發生破碎，直到所有顆粒粒徑均小于0.074 mm，此時級配曲線會成為一條水平線；基于此理論，提出了破碎度指標Br即破碎度Bt與破碎勢Bp之間的比值，其中破碎度Bt反映了當前顆粒級配曲線與破碎前初始級配曲線所圍面積，破碎勢Bp反映了初始級配曲線與水平線所圍面積，如圖11所示。

圖11 破碎度示意圖Fig.11 Schematic diagram of crushing degree

陳子玉等[27]對破碎度指標進行了修正，認為具有分形級配的堆石料，其破碎度指標僅與初始分形維數D0、當前分形維數D、分形維數極限值Du相關，并給出了計算公式：

由式(19)可知，求取極限分形維數是準確計算任一軸向應力作用下的破碎度指標的關鍵。為進一步探討破碎矸石側限壓實和粒度分形之間的內在機理，并求取極限分形維數，可從壓實度和分形維數之間的定量關系進行分析。將式(9)和(11)代入式(16)可以得到壓實度和軸向應力之間的關系：

從圖10可知式(18)可以有效預測級配破碎矸石分形維數和軸向應力之間的關系，故結合式(18)和式(20)，消去應力σ，可得到表征破碎矸石壓實程度和分形變化的壓實-分形模型：

為簡化式(21)，定義任一軸向應力作用下的壓實度和壓實度極限值兩者之間的差值為壓實度增量ΔK：

結合式(17)和(22)，整理并簡化得：

其中：

式中：a1，a2，b1，b2和c2均不等于零。

為分析壓實度增量和分形維數之間的變化規律，選取n=0.2時3種不同級配下ΔK的實驗值和理論值進行對比，如圖12所示。

從圖12可看出，隨著分形維數增大，壓實度增量ΔK不斷減小。ΔK實驗值和理論值之間存在相似變化趨勢，且實驗值和理論值之間的相對誤差小于10%，再次證明式(11)和式(18)在一定誤差允許范圍內的合理性，也說明由式(23)所表征的壓實-分形模型的有效性。ΔK理論值和實驗值存在誤差，主要是顆粒分形統計過程中顆粒形狀的不規則性和篩選規則存在差異以及小部分顆粒質量流失造成的。此外，式(11)和式(18)的擬合精度也是造成誤差的重要原因。

圖12 壓實度增量-分形維數關系Fig.12 Relationship between fractal dimension and degree of compaction

對于式(23)，根據擬合參數計算得知a和b均不為零，且壓實度增量ΔK是一個非負數。因而，有且只有當D等于c2時，ΔK取得最小值，且最小值為零。這表明只有當分形維數D等于c2時，才滿足壓實度和極限壓實度之間差值為零的條件。壓實度和壓實度極限值之間的差值反映了級配破碎矸石的壓實潛能，當壓實度等于壓實度極限值時，試樣被完全壓實。在穩定壓實階段，壓實變形主要是以結構微調、骨架優化為主，大顆粒很難發生再破碎，當軸向應力足夠大時，可以認為試樣被完全壓實，破碎終止。由式(19)可知，分形維數的變化表征級配的破碎度變化，隨著分形維數增大，破碎度也隨之增大。當分形維數趨于分形維數極限值時，破碎度達到極限值，即此時破碎試樣組成的系統內不再發生顆粒的再破碎，達到一種理想狀態下的穩定結構，由此，可得不同級配矸石再破碎后粒度分形維數極限值Du：

將式(18)和(25)代入式(19)得到關于任一軸向應力作用下破碎度Br的計算公式：

從式(26)可知，對于初始分形維數確定的側限壓實條件下的級配，破碎度指標只和軸向應力有關。破碎度隨軸向應力的增大而增大，當破碎試樣的當前分形維數趨于分形維數極限值時，破碎試樣的再破碎程度也達到極限值1。

文獻[28]中將堆石料顆粒發生破碎后的分形維數和破碎前的分形維數差值定義為級配散體顆粒的破碎率。據此，本文將極限級配狀態和初始級配狀態所對應的分形維數極限值和初始分形維數之間的差值定義為破碎潛能，即分形維數增量ΔD：

結合式(18)，(25)和(27)可以得出：

根據應變式(10)和極限位移a1，得出極限應變εlim為

式(12)是由式(11)變形所得，因而結合式(28)可將式(12)變形為

將式(28)和(30)兩邊同時相除，消去中間變量σ，結合式(24)整理并簡化，得到壓實-再破碎關系式：

式(31)左邊表征級配再破碎特性，右邊表征級配壓實特性，且顆粒破碎隨應變變化呈現出收斂特性。在初始未承載狀態，即應變為零時，a2等于分形維數極限值和初始分形維數的差值；在完全壓實狀態即應變趨于應變極限值時，分形維數增量為零，分形維數達到分形維數極限值。因而，對于不同級配破碎矸石，a2的絕對值越大，則表明達到完全壓實時，分形維數增量越大(即破碎潛能越大)，級配越不穩定。結合圖12中a2的絕對值可知，連續級配結構最穩定，間斷15～20 mm粒徑級配結構次之，間斷0～5 mm粒徑級配結構穩定性最弱。

綜上可知，對于側限壓實條件下級配破碎矸石的壓實和再破碎特性的量化分析，式(11)中a1可表征極限位移，b1表征軸向位移隨應力變化趨于穩定的速率。式(18)中的a2可以表征破碎矸石的穩定性，b2表征分形維數隨應力變化趨于分形維數極限值的速率，c2表征再破碎后的分形維數極限值。

6 結論

1)級配破碎矸石軸向位移和軸向應力、分形維數和軸向應力之間分別滿足不同正相關指數函數關系，且函數均具有收斂性，不同級配對應的函數收斂速度不同。

2)級配破碎矸石的壓實階段可分為快速壓實階段(0＜應力σ≤4 MPa)、緩慢壓實階段(4＜應力σ≤12 MPa)和穩定壓實階段(應力大于12 MPa)。快速壓實階段彈性顯著，緩慢壓實階段塑性較強，穩定階段試樣成為接近原巖體的類原巖體。在高應力作用下，當連續級配冪指數n=0.4時，具有較強的抗壓縮性；當細料質量分數為44.2%～58.3%時，間斷15～20 mm 粒徑級配試樣具有較強的抗壓縮性；間斷0～5 mm粒徑級配試樣抗壓縮性能較差。

3)級配破碎矸石破碎度隨軸向應力增大而增大，且試樣的再破碎主要發生在軸向應力為4＜σ≤12 MPa時即緩慢壓實階段。在同一基準級配下，間斷小粒徑級配試樣分形維數隨軸向應力增加變化幅度大，收斂速度快。這說明缺失小粒徑顆粒的級配試樣更容易發生再破碎，級配穩定性較差。

4)采用表征壓實潛能的壓實度增量ΔK和表征分形特征的分形維數D，建立了壓實-分形關系式，其中，參數c2可以表征不同級配的分形維數極限值；通過表征壓實變形的應變和表征再破碎潛能的分形維數增量，建立了壓實再破碎關系式，其中，參數a2的絕對值可以表征不同級配的穩定性，連續級配結構最穩定，間斷15～20 mm粒徑級配結構次之，間斷0～5 mm粒徑級配結構穩定性最弱。