基于隨鉆測井數據預測破裂壓力

郭大立，王玉基，張小栓，辛驊志，康蕓瑋

(1.西南石油大學理學院, 成都 610500; 2.新疆油田公司, 克拉瑪依 834000)

破裂壓力是壓裂施工時的一項重要參數，能夠較精確地預測出破裂壓力值，對于安全施工具有重大意義。因準格爾盆地MH區塊特殊的地質條件，該區塊的油田開發效益遭受嚴重影響，施工現場在壓裂過程中普遍存在油壓過大、排量提升困難、施工壓力高等嚴重問題，導致施工不能正常進行，酸化預處理是降低破裂壓力的一種方式[1]，酸化預處理對巖石破裂壓力的影響也有很多定量的計算方法[2-3]，主要是依據酸損傷變量預測任意時刻的破裂壓力[4-5]。現有的方法大多僅依賴于應力分布和巖石性質等主要因素，缺乏對隨鉆測井數據的利用。通過對流體掃描成像(flow scanner image，FSI)產出剖面測井資料進行全面分析，建立數據驅動的機器學習模型，能夠更好地適應不同區塊的地質條件，發揮更加優良的效果。

目前國內外已經有很多關于破裂壓力的數值模擬預測方法，如Hubbert-Willis(H-W)公式、Haimson-Fairhurst (H-F)公式、黃氏公式等。然而，隨鉆測井參數和實測破裂壓力的回歸預測模型卻鮮有報道。數值模擬方法具有一定的缺陷，主要是一些參數求取困難且模型不能適用于任何地層。在開發過程中收集到一定的壓裂數據資料時，應用數理統計的方法結合其已有的數據資料可以較準確地預測破裂壓力，可以為后續開發提供基礎信息并且節省開發成本，因此，FSI產出剖面測井技術在MH區塊得到了應用，隨鉆測井資料是在施工時直接測量的，受外界影響較小，為預測破裂壓力提供了一些數據資料，所以可以更真實地反映地層巖石特征。但單井一天的FSI測井花費近百萬，極大地增加了該區塊致密礫巖油藏的開發成本，將已經測出的157簇數據作為樣本，利用統計數據建立破裂壓力預測模型，進而降低壓裂成本。

用統計模型預測破裂壓力已經有相關文獻。Ahmed等[6]采用5種方法(包括功能網絡、人工神經網絡、支持向量機、徑向基函數和模糊邏輯)預測破裂壓力并對比分析預測效果，結果表明人工神經網絡預測精度最高；Yan等[7]分別將粒子群優化算法(particle swarm optimization，PSO)與反向傳播(back propagation，BP)神經網絡、極限學習機(extreme learning machine,ELM)和支持向量機(support vector machine，SVM)相結合預測破裂壓力，并將它們預測結果與傳統多元回歸分析(multiple regression analysis，L-MRA)進行比較，預測精度按PSO-SVM、PSO-ELM、PSO-BPNN和L-MRA的遞減順序排列；李昌盛等[8]建立用遺傳算法優化BP神經網絡并將其應用于破裂壓力預測，結果表明預測精度高于數值模擬方法。

準格爾盆地MH區塊的致密油儲層具有低孔和低滲的特點，H-W模型是目前使用最多的模型，但H-W模型預測精度較低，效果較差。非線性映射能力強和學習速度快是廣義回歸神經網絡(generalized regression neural network，GRNN)模型的兩大優點，最終網絡收斂到樣本量積聚較多的優化回歸面，它對樣本較少時的預測效果比其他神經網絡模型更優，對于不穩定的樣本數據也能較好地處理[9]，十分契合所選用的數據特點，與其他模型相比，GRNN模型方便設置參數，操作簡便，只需要調整一個光滑因子就可以調整網絡的性能，對石油工程而言，其具有重要的實用性，所以嘗試利用GRNN建立模型預測破裂壓力。

為降低MH區塊的開發成本和施工危險，現基于MH區塊FSI測井資料，首次提出將GRNN模型應用于該區塊的破裂壓力預測，并對比分析及進行現場實驗，證明該預測模型的有效性，以期為該區塊的油井開發節約成本，并降低施工風險。

1 MH區塊概況

1.1 地質概況

MH區塊位于準格爾盆地瑪湖凹陷中部，探礦面積7 300 km2。該地區地質獨特，主要特點是埋藏深、物性差、非均質性強、巖石塑性，礫石粒徑變化大、天然裂縫不發育等[10-11]，主要是靠壓裂形成的人工裂縫實現石油增產[12-13]。巖性以中礫巖為主，其次為小礫巖和細礫巖。

1.2 資源分布概況

準格爾盆地MH區塊是世界上迄今規模最大的礫巖油田，石油資源豐富，石油資源量156億t，目前已探明的石油儲量為68億t[14]，如圖1所示。

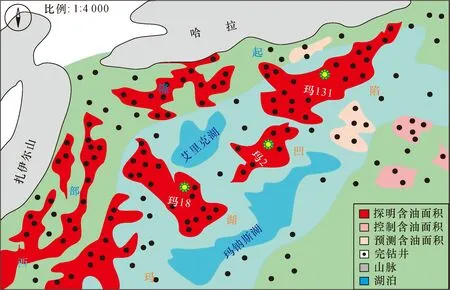
圖1 MH區塊資源分布圖Fig.1 Resource distribution map of MH block

2 模型建立

2.1 數據來源

針對MH區塊所有致密油井，利用FSI產出剖面測井資料和壓裂施工秒點數據共匹配出157簇樣本，其中經過酸預處理后的樣本有51簇，未泡酸的樣本有106簇。MH區塊所有井的酸化預處理工序均一致，采用15%鹽酸，酸液用量固定為5 m3，現場泡酸時間均為30～60 min。

2.2 破裂壓力的計算

根據現場壓裂施工秒點數據可以得到每一級首個發生起裂的簇在起裂瞬間(破裂點)的施工壓力、排量和井底壓力，此時的井底壓力就是首個起裂簇的縫口壓力，而在巖石起裂的瞬間縫口壓力就等于該簇的破裂壓力。任意時刻任意一簇的縫口壓力計算公式為

pf=ps+py-Δpt-Δpm

(1)

式(1)中：ps為井口壓力，MPa；py為液柱壓力，MPa；Δpt為孔眼摩阻，MPa；Δpm為垂直段和水平段的沿程摩阻，MPa。

孔眼摩阻和沿程摩阻的計算公式如下。

(1) 孔眼摩阻[15]計算公式。

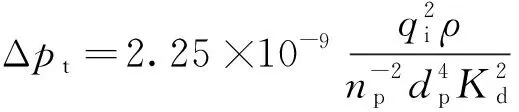
(2)

式(2)中：qi為裂縫入口處的流量，m3/min；ρ為壓裂液的密度，kg/m3；np為該簇的射孔數量；dp為射孔孔眼的直徑，m；Kd為流量系數，孔眼完好時Kd∈[0.5,0.6]，孔眼被完全磨蝕時Kd=0.95。

(2) 沿程摩阻[16]計算公式。

(3)

式(3)中：σ為降阻比；Δp0為清水摩阻，MPa；Q為流體排量，m3/min；D為管柱內徑，mm；L為管長，m；CHPG為稠化劑的濃度，kg/m3；Cp為支撐劑的濃度，kg/m3；當Cp=0(即不加支撐劑)，化簡式(3)就可得出前置液階段的降阻比計算公式。

2.3 參數選取

影響破裂壓力的因素眾多，主要與地層條件、施工條件、裂縫產生方式、油氣井完井方式有關。分析對比已有的破裂壓力預測模型發現其主要與埋深(DEP)、巖石密度(DEN)、泊松比(μ)、自然伽馬(GR)、彈性模量(E)、聲波時差(AC)、補償中子(CNL)、地層電阻率(RT)這8個參數(如表1所示)有關，由埋深、巖石密度和聲波時差可以得出上覆地層壓力與孔隙壓力[17]；泊松比主要反映巖石的塑性，泊松比越大表明破裂壓力越大；自然伽馬主要可以用來劃分巖性；彈性模量可以用來衡量巖石的剛度，其值越大表明破裂壓力也越大；補償中子可以反映出孔隙度大小；隨著埋深增加，電阻率減小，則孔隙度也相應地減小。

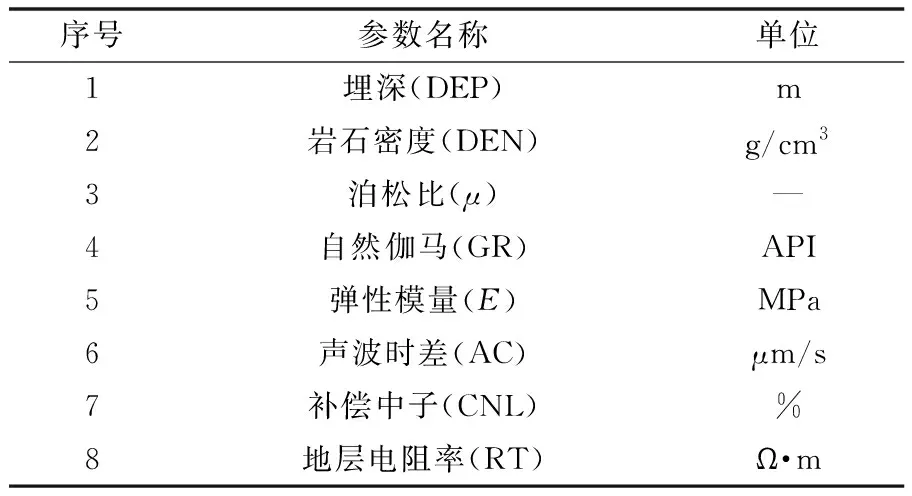
表1 參數詳情Table 1 Parameters for details

2.4 破裂壓力預測GRNN模型

1991年，美國學者Donald F.Specht首次設計并提出了GRNN模型其結合數理統計知識，可根據樣本數據中的隱含關系不斷地逼近真實值，它是一種基于徑向基函數(radical basis function，RBF)改進之后的神經網絡模型，GRNN和RBF的主要區別是在RBF的隱含層與輸入層之間將原來的RBF模型中的權值連接替換成了求和層，訓練集的轉置是連接隱含層與求和層間的權值。GRNN網絡結構[18-19]如圖2所示。

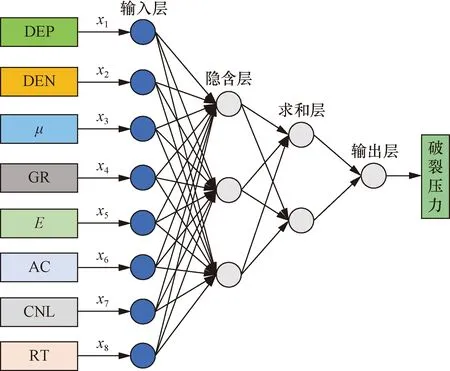
x1～x8表示8個變量圖2 GRNN模型結構圖Fig.2 GRNN model structure diagram

(1) 輸入層。對應網絡的輸入為X=[DEP,DEN,μ,GR,E,AC,CNL,RT]，神經元個數和輸入向量維數相同，先將所有輸入數據標準化處理后再代入模型之中，然后傳遞到隱含層。

(2) 隱含層。隱含層神經元的數量由訓練樣本的數量決定，樣本數據在這一層進行核函數運算后再傳遞到求和層[20]，其中傳遞函數為

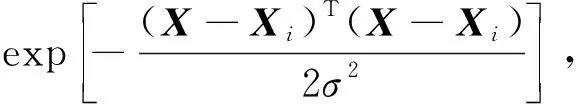
i=1,2,…,n

(4)

式(4)中：X為輸入向量；Xi為第i個學習樣本；σ為光滑因子。給出X，則變量X與學習樣本Xi之間的Euclid距離的平方就作為神經元Pi的輸出值，則為

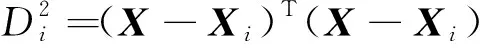
(5)

(3) 求和層。該層節點個數為輸出層節點個數加1,求和層共有兩個輸出節點，其中一個節點的輸出為隱含層輸出結果的算術和，計算公式為

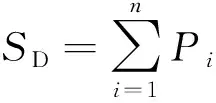
(6)

另一個節點的輸出為隱含層的輸出結果進行加權之后的和，計算公式為

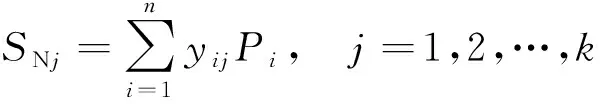
(7)

(4) 輸出層。該層的節點數與訓練樣本的輸出變量個數相同，其計算方式是用上一層的輸出比上上一層第一節點輸出結果，該層節點個數為1，即破裂壓力，計算公式為

實現方式：在施工開始前或深化設計過程中利用BIM技術的可視化及可協調特性對各個專業（建筑、結構、給排水、機電、消防等）的設計進行空間協調，檢查各個專業管道之間的碰撞以及管道與結構的碰撞，避免施工中管道發生碰撞和拆除重新安裝的問題（見圖15、圖16）。

yi=SD/SNj,j=1,2,…,k

(8)

反復調整網絡參數以獲取最優的網絡結構。網絡訓練的方式是交叉驗證，主要優化參數是σ，σ表示GRNN的光滑因子。適應度函數表達式為

fitness=argmin(MSEpredict)

(9)

用訓練后的均方誤差(mean squared error，MSE)作為適應度函數。MSE誤差越小，說明預測數據與原始數據的吻合度就越高。最終優化的輸出未泡酸樣本為0.2，泡酸樣本為0.1。

GRNN預測破裂壓力技術路線如圖3所示。

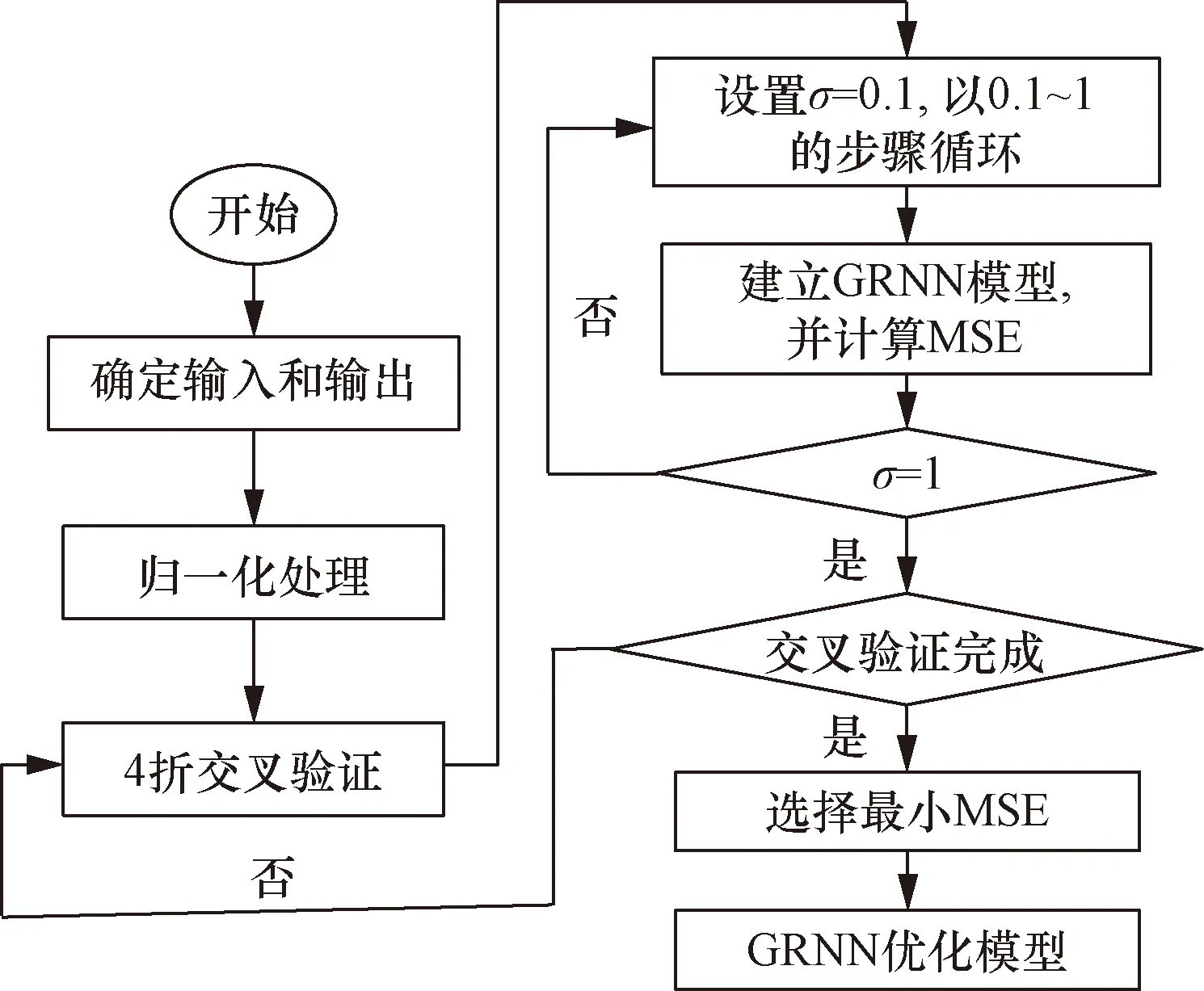
圖3 技術路線圖Fig.3 Technology roadmap

2.5 模型評價

選取均方根誤差(root mean squared error，RMSE)與平均百分比誤差(mean absolute percentage error，MAPE)兩項評價預測模型誤差，計算公式如下。

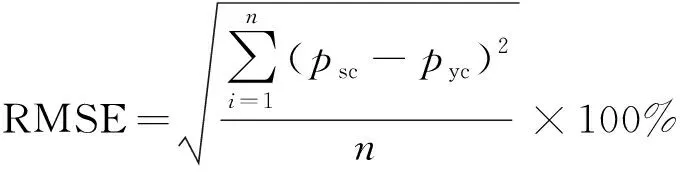
(10)

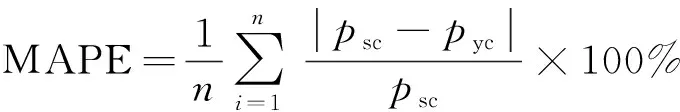
(11)

式中：psc為破裂壓力實測值，MPa；pyc為破裂壓力預測值，MPa；n為樣本數量。

3 實例分析

為了驗證GRNN預測破裂壓力的可行性，現場組織實施了測驗活動，以MH區塊MH-1井為例，施工井段4 120～4 900 m，水平段長度1 858 m，壓裂20級33簇，分為泡酸和未泡酸樣本，泡酸樣本為10簇，未泡酸樣本有23簇。將上述8個參數作為輸入，破裂壓力作為輸出值，并將該井預測結果與BP神經網絡預測結果及H-W模型預測結果以可視化方式展現出來，可以更直觀地突出GRNN模型相比于其他破裂壓力預測模型的優勢。

表2給出了MH區塊MH-1井部分測井數據，表2中的1～23序號數據為未泡酸樣本，24～33序號數據為泡酸樣本。

表2 MH區塊MH-1井部分測井數據Table 2 Partial log data from well MH-1 in Block MH

從單井各級的施工曲線可以得到每一級第一個發生起裂的簇在起裂瞬間(破裂點)的施工壓力、排量和井底壓力，此時的井底壓力等于第一個起裂簇的破裂壓力。計算井底壓力的過程中，需要根據秒點數據時刻考慮排量、砂濃度和井口壓力的變化，這樣得到的縫口壓力才具有可靠性。各個簇在起裂的瞬間，壓裂液僅在管柱中壓縮形成憋壓狀態，孔眼處無壓裂液經過，故此時的孔眼摩阻為0。一旦某一簇被壓開，井筒中的壓裂液會以該簇的射孔為突破口擠入縫內，不會經過該簇之后的所有簇，故該簇之后的沿程摩阻為0。

應用FSI流動掃描技術可以得到不同井各級的產出剖面測井解釋結果，如圖4所示。從解釋結果可以確定不同簇的射孔位置處是否有產出(產油、產水和產氣)，故可以確定該簇是否被壓開，從而可以明確任意一段具體是哪幾簇已經起裂。

根據壓裂施工秒點數據可以得到不同井各級的施工曲線。如圖5所示，施工曲線上井底壓力的首個峰值即是最小主應力最小的簇的破裂壓力。砂堵后(第一次加砂完畢后)繼續壓裂，施工曲線上的井底壓力會出現第二個峰值，若該值大于第一個峰值則表明砂堵成功，施工曲線出現兩次峰對應的FSI產液剖面測井資料也應該對應出現兩個射孔有液體產出，這樣才能確定是有新的簇被壓開，意味著最后發生起裂的簇是破裂壓力更大的新簇，也是所有起裂的簇中破裂壓力最大的簇，其對應的最小主應力在所有起裂的簇中也最大。若第二個峰值小于第一個峰值則表明砂堵失敗，意味著沒有新簇發生起裂，只是在砂堵前就已經起裂了的老簇再次被打通，故此種情況下的第二個峰值便無參考意義。

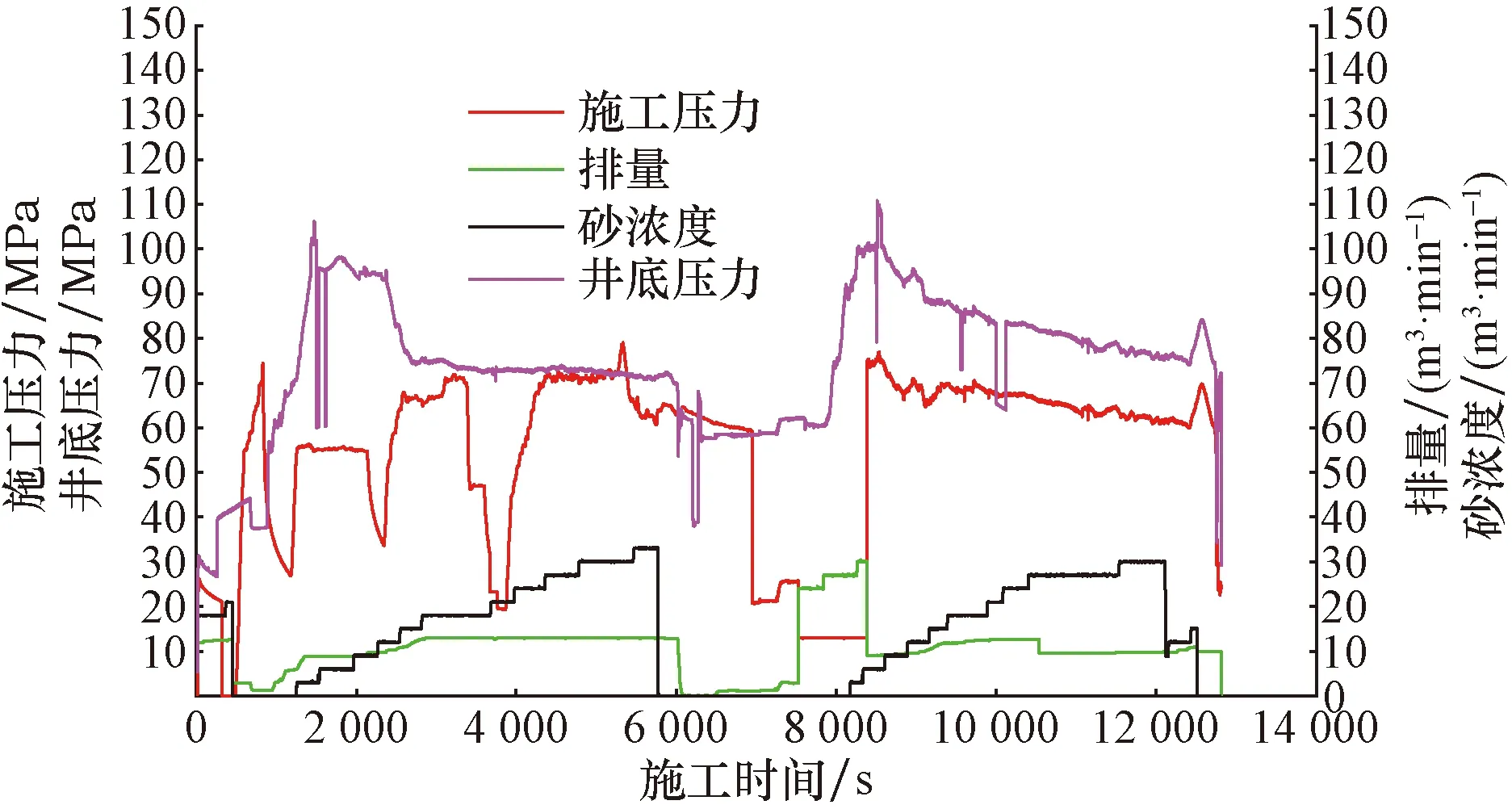
圖5 MH區塊MH-1井第20級施工曲線Fig.5 Construction curve of class 20 of well MH-1 in MH Block

根據測井數據可以計算得到破裂點的井底壓力(即起裂簇的破裂壓力，如圖5所示)，利用FSI產出剖面測井資料可以準確得出單井每段具體是哪幾簇起裂(如圖4所示)。各簇按照破裂壓力由低到高的順序(也是最小主應力由低到高的順序)依次起裂，故綜合兩個結果就可以將破裂壓力與起裂的簇進行匹配，從而確定首次和末次發生起裂的兩個簇的破裂壓力真實值，中間發生起裂的簇其破裂壓力無法進行匹配。

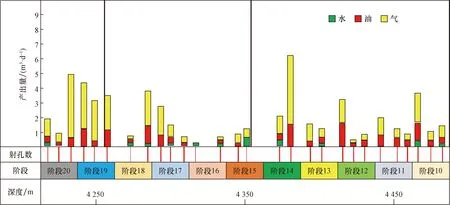
圖4 FSI生產剖面測井解釋結果圖Fig.4 FSI production profile log interpretation result diagram

3.1 不同模型對比

為討論酸預處理對巖石破裂壓力的影響，對泡酸樣本和未泡酸的樣本分開建立GRNN模型，并與BP神經網絡模型和H-W模型預測的結果進行比較，H-W模型的計算方式為

pb=3σh-σH+σf-po

(12)

式(12)中：pb為破裂壓力，MPa；σh為最小主應力，MPa；σH為最大主應力，MPa；σf為巖石抗張強度；po為孔隙壓力，MPa。

3種預測模型預測結果與實測破裂壓力值的對比分析結果如圖6所示。

圖6是對泡酸樣本和未泡酸樣本分開建立3種模型，對比分析預測效果，可以直觀看出，無論是泡酸樣本還是未泡酸樣本，3個模型中GRNN模型預測效果都是最佳。由于無法對泡酸后的巖石樣本進行現場取樣，所以沒有進行電鏡掃描實驗，故無法確定酸處理后巖石彈性模量和脆性指數等參數的取值，因此不能利用H-W公式計算泡酸后的巖石破裂壓力。故僅對未泡酸的樣本進行破裂壓力H-W模型計算。根據建立的模型分別對泡酸和未泡酸樣本進行預測精度對比分析，結果如表3所示。

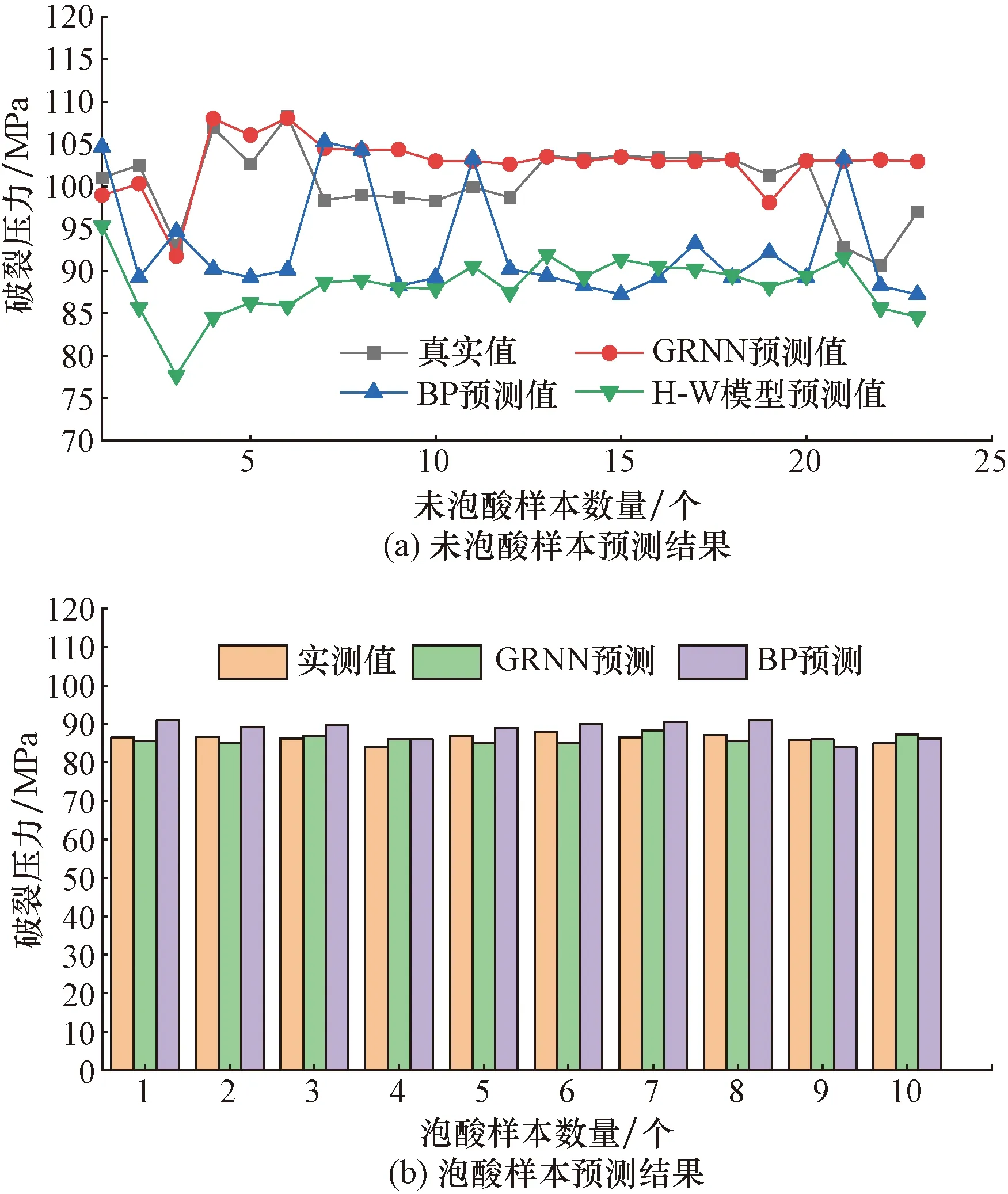
圖6 未泡酸樣本和泡酸樣本的預測結果與實測值對比圖Fig.6 Comparison of predicted results and measured values of unfoamed acid and foamed acid samples

由表3可知，GRNN模型的預測誤差在3個模型中是最小的，而且無論是未泡酸樣本還是泡酸樣本，GRNN模型的預測誤差浮動較小，所以,GRNN模型可以更好地預測MH區塊的破裂壓力值。

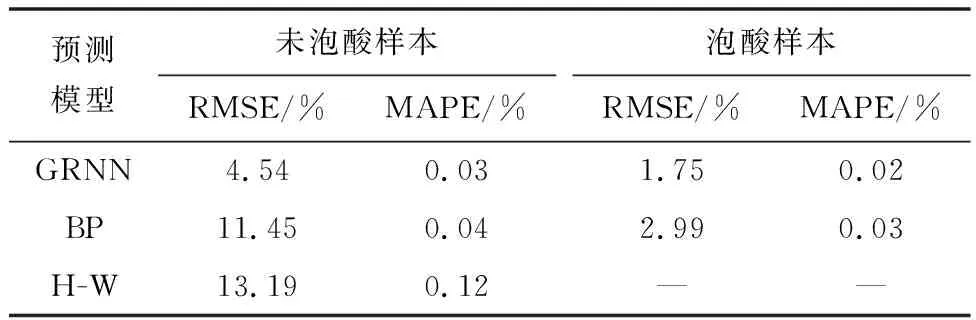
表3 3個模型預測誤差對比Table 3 Comparison of prediction errors of the three models

3.2 泡酸分析

針對MH區塊的所有致密油井，按現場的區塊劃分為A、B、C三大區塊并分別統計了泡酸和未泡酸井的平均破裂壓力，并從數據的角度出發，根據統計結果給出了不同區塊的酸化預處理建議，具體結果如表4所示。

從表4可以看出，A區塊的井泡酸與否結果并無明顯差異，根據統計結果可建議A區塊的井壓裂施工不進行酸化預處理，這樣能夠在保證同等壓裂效果的同時降低一定成本。B、C區塊經過泡酸之后，破裂時的排量明顯較大，這表明酸化預處理能夠為大排量施工提供保障，而且能降低壓裂過程中的風險。

表4 MH區塊井分區塊統計結果Table 4 Statistical results of well blocks in MH block

同時，經過酸化預處理之后，B、C區塊的破裂壓力顯著下降，為壓裂過程中井底憋壓提供了更大空間，降低了施工風險，因此建議B、C區塊其余井同樣進行酸化預處理。

3.3 應用于不同區塊對比分析

在研究了MH區塊后，對AH區塊136條數據進行預測并與MH區塊進行對比分析。將AH區塊的8個主控因素作為輸入，利用GRNN 模型進行預測，預測誤差分析如表5所示。

由表5可以得出，GRNN模型預測AH區塊破裂壓力效果較好，與MH區塊的預測誤差對比浮動較小，所以GRNN模型預測破裂壓力具有普適性。

表5 AH與MH區塊對比分析Table 5 Comparative analysis of AH and MH block

4 結論

由于MH區塊的酸化預處理工序固定且單一，因此僅從統計角度進行定性分析給出不同區塊的酸化預處理建議。針對不同的酸液類型以及酸液濃度、酸液用量和酸化時間進行大量的實驗從而給出最優的酸化預處理方案仍是值得研究的問題。通過綜合分析得出以下結論。

(1) 綜合利用FSI產出剖面測井資料和現場壓裂施工秒點數據確定了單井各段不同簇的破裂壓力真實值。

(2) 綜合利用FSI產出剖面測井數據資料和地質參數建立預測巖石破裂壓力的GRNN模型。GRNN模型考慮了埋深、泊松比、彈性模量、巖石密度、自然伽馬、聲波時差、補償中子、地層電阻率這8個主要影響因素，通過現場實驗驗證，結果證明，該模型相比于BP神經網絡和H-W模型具有更好的普適性及可靠性。

(3) 酸化預處理可以起到降低儲層破裂壓力作用，為壓裂過程中的井底憋壓提供更大的空間，合理地對油井進行酸化預處理不僅可以降低施工風險，保證壓裂施工的有效性，而且可以為油井開發節省成本。