基于零知識證明的匿名投票方案

于筌，劉曉彤，刁恩虎，劉秀磊*

(1.北京信息科技大學北京材料基因工程高精尖創新中心，北京 100101； 2.北京信息科技大學數據與科學情報分析研究所，北京 100101)

電子投票是互聯網時代常用的決策手段，第一個電子投票協議由Chaum[1]在1981年提出，該協議使用公鑰密碼學技術，解決了不可信通信環境下的投票安全問題。現有的大多數電子投票方案均依托于中心化節點，使用諸如盲簽名[2]等密碼學技術對投票過程進行加密。中心化架構具有系統結構簡潔、響應速度快等特點，但同時也存在諸多不足。從系統需求的角度，中心化系統易被單點攻擊，公信力不強；從加密算法的角度，中心化系統所基于的各種密碼學算法限制了系統的構建：基于盲簽名的電子投票系統[3]無法完全隱藏投票者身份信息；基于秘密共享的電子投票系統[4]通信復雜度較高[5]；基于混合網絡的電子投票系統[6]雖然可以完成匿名投票，但需要多個混合服務器，系統成本較高。

以太坊(Ethereum)[7]和零知識證明(zero knowledge proof)[8]技術的出現為這些缺陷提供了解決辦法。以太坊是去中心化系統的代表，它的數據分布于全球礦工節點，智能合約在以太坊上基于共識機制運行，具有透明性和可信性。所有礦工節點保存著一份公認的合約執行結果，因此在區塊鏈上運行的智能合約結果具有不可篡改性。現有很多系統選擇使用區塊鏈作為其底層結構來提升安全性，如基于區塊鏈技術的數據共享系統[9]、基于聯盟區塊鏈的水產養殖品質量追溯系統等[10]。在電子投票領域，基于區塊鏈的一個典型應用是當前實現在鏈上的各種不具備匿名性的去中心化自治組織(decentralized autonomous organization，DAO)，其通過智能合約運轉，具有較高的透明度和投票參與率，是未來區塊鏈發展的重要方向。零知識證明由Goldwasser等[8]在1985年提出，旨在讓證明者可以在不為驗證者提供任何有用信息的情況下，使驗證者相信某個論斷正確。將零知識證明應用于鏈上的投票系統，可使投票者在不透露任何身份信息的前提下完成投票。

現從基本的非匿名智能合約鏈上投票系統出發，使用零知識證明技術對智能合約進行改進，以滿足可重復匿名投票與不可重復匿名投票的應用場景，彌補原始鏈上投票系統的缺陷，使最終投票系統同時具備匿名性與不可偽造性。上述系統除滿足常見投票場景外，亦可滿足涉及隱私的問卷調查場景，進一步彰顯本系統的價值。所有智能合約、合約部署步驟及相關交互代碼均已開源，期望能為相關系統開發人員提供有益的參考。

1 相關技術

1.1 橢圓曲線密碼

橢圓曲線密碼 (elliptic curve cryptography)[11]是指利用橢圓曲線的特性來實現如公鑰加密、共享密鑰等技術的統稱。與其他密碼算法相比，其優勢在于相同長度下密碼強度高。由美國國家標準與技術研究院(National Institute of Standards and Technology，NIST) SP800-57文件[12]可知，長度250 bit左右的橢圓曲線密碼與長度為2 048 bit的RSA(Rivest-Shamir-Adleman)密碼具有近似的強度。使用對零知識證明電路設計友好的橢圓曲線Baby Jubjub[13]加密投票者身份信息，以保證投票方案的匿名性。

1.2 單向散列函數

單向散列函數是指可以將消息映射到散列值的函數，常見散列函數有SHA-256[14]、RIPEMD-160[15]、皮特森哈希(Pedersen Hash)[16]等。它需滿足以下3種性質：抗碰撞性、隱秘性和謎題友好性。抗碰撞性是指函數難以人為產生哈希碰撞；隱秘性是指函數只能單向計算；謎題友好性是指函數輸出值不可預測。為滿足投票的實時性，選擇使用電路精簡、運行速度快的皮特森哈希。皮特森哈希的生成過程如下。

(1)對域名分隔符、數組[0,1,…,63]使用blake2s-256散列函數[17]生成散列值，再將散列值使用映射函數在Baby Jubjub曲線上映射生成64個點[G0,G1,…,G63]。

(2)將輸入的位數用0填充至3的倍數。

(3)按照每塊189 bit分塊。

(4)再將每塊按照每片3 bit分片，共63片。

(5)每片使用式(1)進行計算，其中mj代表此塊中的第j片，s0、s1、s2分別為第j片的第1、2、3位。

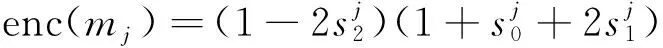
(1)

(6)將每片結果再乘以24j。

(7)所有結果相加得到H。

(8)計算[HG0,HG1,…,HG63]，得到[P0,P1,…,P63]。

(9)計算P0+P1+…+P63，得到皮特森哈希基點。

(10)對皮特森哈希基點進行哈希抽取，抽取其x值作為最終皮特森哈希值。

1.3 非交互式零知識證明

非交互式零知識證明(non-interactive zero knowledge proof)[18]是一種特殊的零知識證明，證明者可以在不與驗證者交互的情況下生成證明，以此排除證明者與驗證者串通的情況。由于非交互式零知識證明協議允許智能合約充當驗證者，因此非常適用于以太坊應用程序。在這種情況下，任何人都可以生成證據并將證據作為交易的一部分發送給智能合約，智能合約對證據進行驗證后，根據結果執行后續操作。

最常用的非交互式零知識證明協議是簡潔的非交互式零知識證明(zero-knowledge succinct non-interactive argument of knowledge，zk-SNARK)[19]。它是具有簡潔證明和次線性驗證時間的非交互式零知識協議，因其較高的可編程性而被大多數以太坊開發人員所接受。

在眾多zk-SNARK算法中，Ronald Mannak對比了8種主流的zk-SNARK算法的性能參數[20]，Fractal[21]、Halo[22]、SuperSonic[23]、Plonk[24]、Marlin[25]、Sonic[26]、Groth16[27]、zk-STARK[28]。研究表明，在證明數據量大小和驗證速度方面，Groth16遠好于其余算法[20]。因此使用Groth16算法作為系統核心算法，以達到減少投票成本、提升投票速度的目的。

2 基于智能合約的投票系統

基于智能合約的投票系統結構如圖1所示，系統由鏈上智能合約與前端用戶交互界面組成。智能合約負責提供基本投票功能、存儲投票結果，并將投票過程標識為相應事件，以便用戶從以太坊區塊中查看。前端交互界面部分通過MetaMask瀏覽器錢包插件與鏈上智能合約進行交互。系統具體投票步驟如下。

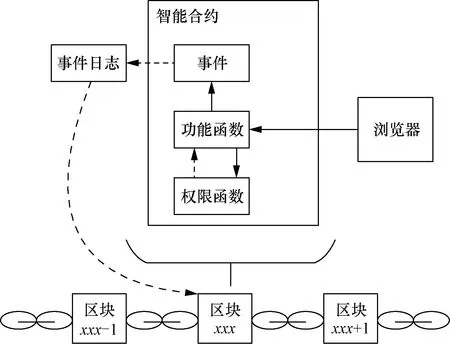
實線箭頭代表函數調用；虛線箭頭代表數據傳輸圖1 基于智能合約的投票系統結構Fig.1 The architecture of the voting system based on smart contracts

(1)用戶連接MetaMask錢包，通過前端頁面訪問智能合約。

(2)智能合約使用權限函數通過訪問者地址對訪問者身份進行認證。

(3)認證通過后，用戶調用功能函數進行投票。

(4)待投票結束后，合約返回投票結果至前端，以供用戶查看。

3 基于零知識證明的匿名投票方案

上述實現的投票系統雖然通過地址對訪問者身份進行了判斷，在一定程度上保證了投票過程的安全性，但這種驗證方式并不具備匿名性。在這種地址與投票權一一綁定的驗證方式中，攻擊者可以對地址的交易信息進行分析，構建用戶畫像，進而獲取投票者部分身份信息。為了避免投票者身份信息泄露，系統需選擇一種可以完全隱藏身份信息的方法。首先，采用數字簽名技術標識投票者，將用于數字簽名的公私鑰稱為投票私鑰Pr和投票公鑰Pb，以鏈下形式分發；其次，使用零知識證明技術隱藏Pr與Pb之間的關系，從而達到匿名投票的目的。

由于零知識證明方法會完全隱藏投票者特有信息，因此該方案無法滿足不可重復投票的應用場景。為提高其通用性，在方案中加入皮特森哈希作為投票者的特征信息。智能合約可通過投票者發送的Pr的皮特森哈希來記錄每個投票者的投票次數，以消除惡意投票者對投票過程的影響。引入的皮特森哈希既與Pb無直接關系，又可以保護Pr，使該方案滿足匿名性的同時提高了通用性。

圖2所示的匿名投票方案的具體運行流程分為5個階段，分別為準備階段、發布投票階段、投票階段、驗證階段和計票階段。下面將對每個階段的算法進行介紹，其中表1記錄了算法中用到的主要參數及其代表符號。

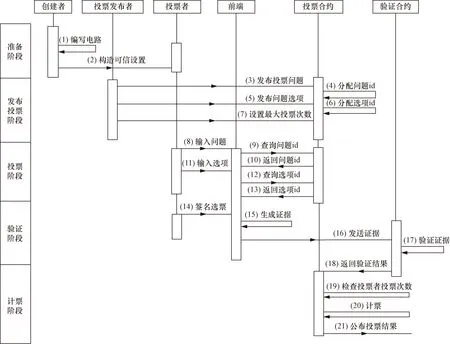
圖2 匿名投票方案運行流程Fig.2 Anonymous voting scheme operation process

表1 主要參數Table 1 Primary parameters

3.1 準備階段

系統準備階段共分為兩個部分，編寫零知識證明算術電路和構造可信設置，對應圖2中的步驟1、步驟2。

方案創建者首先需編寫零知識證明算術電路。電路描述構造和驗證零知識證明證據時需遵循的約束規則，其輸入分為私有輸入與公有輸入。 私有輸入包括所有證明者想要證明的秘密，對驗證合約不可見；公有輸入包含私鑰哈希、投票者投票選擇等投票信息，對驗證合約可見。

算法1：零知識證明算術電路。

私有輸入：Pr,R;

公共輸入：PbG,H′,R′;

Pb= GenPublicKey(Pr);

(2)fori= 1,2,3,…,len(PbG) do:

(3)/*約束投票公鑰必須在投票公鑰組中*/

PbG[i]=Pb;

(4)end for

H= GenHash(Pr) ;

(6)/*約束投票私鑰的哈希與合約接收的投票私鑰哈希一致*/

(7)/*約束投票選擇與合約接收的投票選擇一致*/

構造可信設置即使用算術電路生成用于進行零知識證明的兩組隨機數：Pk和Vk。隨后方案用得到的Pk和Vk生成驗證合約，驗證合約用于在驗證階段對智能合約的訪問者進行身份驗證。

3.2 投票發布階段

在投票發布階段，投票發布者會發布投票問題和相應選項至投票合約，并設置每個投票者最大投票次數。投票發布階段算法如算法2所示，對應圖2的步驟(3)～步驟(7)。

算法2：投票發布算法。

輸入：Vq,Vo,Vmax;

輸出：Qi,Oi;

(1)PsendVqtoSt;

(2)StassignQitoVq;

(3)returnQitoP;

(4)fori= 1,2,3,…,do:

(5)Psend (Vo,Qi) toSt;

(6)end for

(7)StassignOitoVo;

(8)returnOitoP;

(9)PsendVmaxtoSt;

(10)StsaveVmax;

3.3 投票階段

在投票階段，投票者將其選擇輸入前端，前端與合約交互得到相應問題與選項的id，以便在驗證階段完成電路約束，生成證據。投票算法如算法3所示，對應圖2的步驟(8)～步驟(13)。

算法3：投票算法。

輸入：Vq,Vo;

輸出：R;

VrequireQifromSt;

returnQitoV;

VrequireOifromSt;

returnOitoV;

R=[Qi,Oi];

3.4 驗證階段

在驗證階段，驗證合約驗證訪問者是否擁有投票權限。投票者需要對投票選擇進行簽名，前端根據其投票私鑰生成證據，并將證據、投票私鑰哈希和在投票階段獲得的相應id發送給驗證合約。驗證合約根據證據檢查投票者身份和投票選擇的正確性。驗證階段算法如算法4所示，對應圖2的步驟(14)～步驟(18)。

算法4：驗證算法。

輸入：Pr,PbG,R;

(1)H= GenHash(Pr);

(2)Ci=[Pr,PbG,H,R];

(3)W= Calculate Witness(Ci);

(4)Pi= Slice(W);

(5)/*使用見證和證明密鑰生成證據*/

π= Prove(W，Pk);

(6)/*投票者發送證據到驗證合約*/

VsendπtoSv;

(7)/*驗證合約驗證訪問者身份*/

if Verify(π，Pi):

(8)SvsendR′ toSt;

(9) else

(10) visitor is not a voter;

(11)end if

3.5 計票階段

當訪問用戶被確定是投票者后，驗證合約將信息發送給投票合約，方案進入計票階段。在計票階段，投票合約需先驗證投票者的投票次數是否符合規范。如果符合，則將投票計入；否則，將投票作廢。投票結束后，投票合約根據投票選擇將得票最多的選項設置為最終投票結果。計票階段算法如算法5所示，對應圖2的步驟(19)～步驟(21)。

算法5：計票算法。

(1) ifH′ not in HL:

(2) PutH′ in HL；

(3) else:

(4) ifVc

(5) vaild vote;

(6) else:

(7) invaild vote;

(8) end if

(9) end if

(10) after voting:

(11)Stcalculate final results;

(12) return final results;

4 方案分析

提出的匿名投票方案不僅滿足Fujioka等[29]在1992年提出的電子投票系統應具有的7種基本安全性質：合格性、匿名性、不可重復性、完整性、正確性、公平性和可驗證性，還滿足穩定性和通用性。

4.1 安全性分析

4.1.1 合格性

合格性指沒有投票權的用戶無法進行投票。在本文方案中，驗證合約需要根據訪問者提交的證據驗證訪問者的身份，給予其相應的投票權限。只有擁有投票私鑰的投票者能生成正確的證據，執行投票操作，因此方案滿足合格性。

4.1.2 匿名性

匿名性指所有投票者信息應被保密。本文方案分兩步完成投票匿名性。第一步，方案使用數字簽名和零知識證明技術解除了投票權對地址的依賴，使投票者可以通過任意以太坊地址進行投票，消除了投票者真實以太坊地址暴露的隱患。第二步，方案用于與鏈上合約交互的數據和合約中保存的數據均不包含任何投票者身份信息，防止攻擊者通過合約竊取投票者相關信息。至此方案滿足匿名性。

4.1.3 唯一性

唯一性指投票者在某些場景下不可重復投票。本文方案采用投票私鑰哈希作為特有信息標識投票者。在不可重復的投票場景中，投票合約可以通過此標識判斷投票者投票情況。因此方案滿足唯一性。

4.1.4 完整性

完整性指所有有效選票都被正確計算。對方案驗證階段和計票階段的投票完整性進行分析。在驗證階段，方案使用零知識證明技術約束投票者的投票選擇無法被篡改。在計票階段，因智能合約具有原子性，投票合約接收的正確的投票選擇一定會按照規定好的投票規則計入結果。因此方案滿足完整性。

4.1.5 正確性

正確性指所有無效選票都不被計算。本文方案共有兩種出現無效選票的場景，一種是投票者投票次數超出投票發布者規定的最大投票次數，另一種是攻擊者篡改投票者正確的投票選擇后生成偽造選票。

針對第一種場景，方案在驗證階段通過檢查投票者的投票次數對其進行甄別。針對第二種場景，由于偽造選票不滿足零知識證明算術電路的約束，因此其無法通過驗證合約的檢測。至此兩種無效選票均無法計入投票結果，方案滿足正確性。

4.1.6 公平性

公平性指投票中間結果不可被獲取。本文方案雖然在投票結束前不會公布投票結果，但每個投票者的投票選擇會伴隨交易記錄保存在以太坊中。由于投票選擇采用明文傳輸，攻擊者可以通過交易記錄中的數據計算出中間投票結果。針對上述場景，方案可通過合理設置投票時間來避免中間投票結果泄露，滿足公平性。

4.1.7 可驗證性

可驗證性指投票結果不會被偽造。本文方案在以太坊上運行，投票過程的每一步和投票結果都通過交易記錄和事件日志被記錄在以太坊分布全球的節點中，具有不可篡改性。因此投票結果與投票過程均不可篡改，方案滿足可驗證性。

4.1.8 穩定性

穩定性指系統抗干擾的能力。本文方案是去中心化的投票方案。方案不會因節點故障等中心化系統常出現的問題，造成投票數據丟失、投票系統崩潰等嚴重后果，因此方案穩定性較強。

4.1.9 通用性

通用性指系統適用于不同應用場景的能力。本文方案可同時滿足可重復匿名投票和不可重復匿名投票兩種投票場景，且支持投票發布者根據自身需求設置每個投票者的最大投票次數，具有良好的通用性。

4.2 方案對比分析

通過將本文方案與已提出的電子投票方案進行對比分析(表2)，表明本文方案基本解決了電子投票系統常見的安全問題。

表2 方案對比Table 2 Comparison of schemes

文獻[30]提出的投票方案雖然在文獻[29]提出的方案上進行改進，解決了選票碰撞問題，增強了方案的安全性。但其仍然是中心化投票方案，嚴重依賴可信第三方，因此不滿足投票匿名性、可驗證性和穩定性。文獻[31]和文獻[32]提出的電子投票方案將保存的以太坊地址作為投票者特有信息來驗證投票唯一性。與第3節描述的方案相同，這種方式限制投票者只能使用特定的以太坊地址進行投票，雖然沒有直接暴露投票者身份信息，但攻擊者可以由此得到投票者真實以太坊地址，進而獲取投票者真實身份信息，方案不滿足匿名性。文獻[30-32]提出的電子投票方案雖然分別使用可信第三方分配的身份標識和以太坊地址作為投票者特有信息對投票唯一性進行判定，但3種方案均未考慮可重復投票場景，不滿足通用性。文獻[33]中提出的方案使用一次性環簽名算法，滿足電子投票系統的基本安全要求。但方案無法同時滿足可重復投票和不可重復投票場景，通用性差于本文提出方案。和上述3種方案相比，本文方案滿足電子投票方案應具有的安全特性，且具備更好的通用性，可以滿足各種不同的應用場景。

5 結論

提出一種結合零知識證明與數字簽名技術的鏈上匿名投票方案。該方案可以使投票者在不暴露任何身份信息的前提下完成投票，并通過算術電路來約束投票過程的完整性和正確性。借助以太坊去中心化、透明、不可篡改等特點，實現了投票可驗證性和系統穩定性。經過對比分析，方案在滿足電子投票系統基本安全特性的同時，還具備比已提出的電子投票系統更好的通用性，適用于不同的應用場景。