二維蜂窩狀光子晶體能帶的數學模型與仿真研究

楊 之

（北京郵電大學，北京 100876）

光子晶體是由宏觀光學介質代替微觀粒子按一定規律周期性排列的人工微觀結構，其周期陣列限制了電磁波在光子晶體中的傳播，對特定波長的光子具有阻擋作用，從而形成了光子帶隙[1]。根據應用需要設計光子晶體的結構，由于光子帶隙的存在可以禁止光在一定頻率范圍內的傳播，使得光子晶體有著廣泛的應用，其應用包括窄帶濾波器、分復用器等[2-5]。獲得寬的光子晶體帶隙是設計高性能光子晶體器件的基礎[6]，所以如何設計光子晶體結構來獲得更寬的帶隙一直是光子晶體領域的研究重點。

已有研究結果表明，二維蜂窩狀光子晶體具有較大的帶隙[7]，且帶隙大小和介質柱的半徑大小與介電常數密切相關[8-9]。改變光子晶體的晶格結構、降低結構對稱性和引入新材料等措施都可以增大光子晶體的帶隙，但是由于直接進行實驗來設計新型光子晶體結構的成本巨大，現在一般先采用數值模擬方法進行結構設計，以期獲得結構設計的指導。目前，數值模擬二維光子晶體帶隙的常用方法有平面波展開法[10-11]、時域有限差分法[2，12]和有限元方法[13]，其中有限元方法因其計算效率較高，常用于三角晶格光子晶體和正方晶格光子晶體的數值模擬，但目前在蜂窩狀光子晶體領域研究較少。

本文采用有限元法研究二維蜂窩狀光子晶體的能帶結構，以往在對蜂窩晶格光子晶體進行建模時通常選擇正六邊形結構作為單元晶格，本文在數值模擬過程中直接采用了易于操作的三角晶格胞元，使建模仿真和邊界處理更加容易。并利用COMSOL 軟件計算了二維蜂窩狀光子晶體的能帶結構，通過對比文獻[14]的結果，驗證了方法的正確性和有效性。進一步，本文采用數值模擬的方法探究了二維蜂窩狀光子晶體的參數與帶隙的關系，并通過在蜂窩狀光子晶體中應用新型材料構造了寬帶隙的新型二維蜂窩狀光子晶體結構。

1 能帶結構計算的數學模型

在本節中，將介紹二維蜂窩狀光子晶體能帶求解的數學模型。考慮由周期介電圓柱組成的二維蜂窩狀光子晶體陣列，如圖1（a）所示，a0為晶格常數，即相鄰2 個正六邊形中心的距離，a1和a2是長度a0的向量。放大的單個六角蜂窩晶格如圖1（b）所示，其中R 為六邊形的邊長，d 為圓柱體的直徑，εa和εb分別是周圍背景和介電圓柱的介電常數。本文采用三角晶格胞元進行數值計算，光子晶體等效至xoy 平面后選取的三角形晶格胞元，如圖1（c）所示，其邊長為a0。

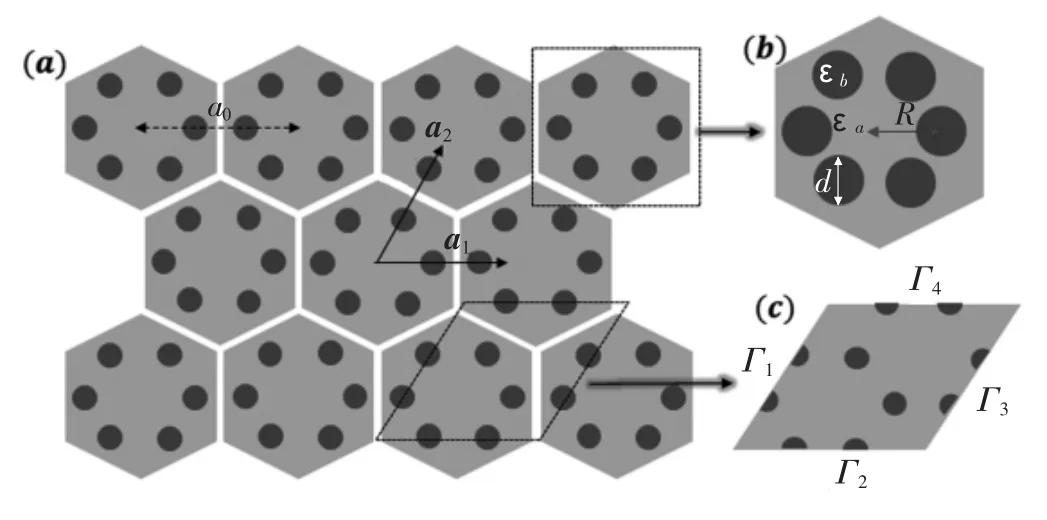
圖1 蜂窩狀光子晶體示意圖

圖2 三角晶格第一布里淵區

下面根據圖1（c）所示的三角單元晶格，推導光子晶體特征值問題。在經典電磁理論中，電磁現象可由Maxwell 方程組（1）描述。在光子晶體中，研究的對象是電磁波，其在光子晶體中傳播時滿足Maxwell 方程組

式中：E 是電場強度；H 是磁場強度。對于二維光子晶體，直接對Maxwell 方程進行求解比較困難，由于電磁波可分解為簡諧波，即有E（r，t）=E（r）e-iωt，H（r，t）=H（r）e-iωt，這里ω 是頻率。代入式（1）可得到與時間變量無關的Helmholtz 方程，即電場方程（2）和磁場方程（3）

考慮二維光子晶體帶隙問題時，可簡化為TM 和TE 兩種偏振情形。在TM 模式下，有E（r）=（0，0，ER（））；在TE 模式下，有H（r）=（0，0，HR（））。這里是二維坐標（x，y）。代入式（2）和（3），分別可以得到TM 模的電場波動方程（4）和TE 模的磁場波動方程（5）

由于二維光子晶體的周期性，滿足Bloch 定理，可將上述波動方程化至單位原胞上再進行數值實驗。在二維情況下，記，k=（a，b）表示的是二維平面空間內的波矢矢量，其取值范圍為不可約布里淵區B。首先考慮TM 模

Ω 是求解的二維集合區域，在單位原胞邊界∏=?Ω上，滿足邊界條件

式中：Γ1和Γ3是單位原胞的一組對邊；Γ2和Γ4是單位原胞的另一組對邊。求解區域如圖1（c）三角單元晶格所示。

求解TE 模的過程類似，為方便討論變分過程，可將2 種模式統一記成如下特征值形式，給定矢量k，求λ 和uR使得

uR表示待求場量即特征向量。只要矢量k 遍歷第一不可約布里淵區域的邊界，就能夠繪制出能帶結構圖。

下面針對式（8），給出其有限元變分過程和離散過程。首先，定義Sobolev 空間

對于固定的波矢k，當求解區域是線性三角元時，u、v在單元e 內的近似ue、ve，取線性三角元的基函數和的線性組合，這里所說的基函數是關于（x，y）的勢函數，不妨取試探函數ve為單元基函數，則有

這里x 取值{i，j，k}，而ui，uj，uk是待定常數。

根據SRSS評分,擬定療效評定標準,分為顯效、有效、無效3個指標:(1)顯效:治療后,SRSS評分降低>50%。(2)有效:治療后,SRSS評分降低25%-50%。(3)無效:治療后,SRSS評分降低<25%[3]。

由此得到單元剛度矩陣，然后根據線性三角元局部編號和整體編號關系，生成總剛度矩陣A 和B，得到變分問題對應的離散特征值問題：

在求解廣義特征值問題時，還需要考慮周期邊界條件（7），從而得到最終的待求解廣義特征值問題

對于形如（14）的廣義特征值問題，在二維蜂窩狀光子晶體帶隙模型中，矩陣A 和B 常具有正定性，則有Cholesky 三角分解

則對式（14）兩側的左側乘L-1，并在右側整理提出因子LT得

式（16）可以看成以λ 為特征值，LT為特征向量的特征值問題，并且式（16）和（14）具有相同的特征值，系數矩陣仍滿足正定性，這樣就將廣義特征值問題（14）轉化為特征值問題（16），可利用直接法或迭代法進行求解特征值問題（16）。

2 數值仿真結果

2.1 算例1：二維蜂窩狀光子晶體仿真

本節考慮圖1 所示的二維蜂窩狀光子晶體，周圍背景的介電常數是εa=1，圓柱體的介電常數是εb=11.7，六邊形的長度為R，圓柱體截面圓形的直徑為d且d=2/3R。選擇三角單元晶格模擬得到的能帶圖如圖3 所示，在其他參數不變的情況下，僅改變晶格參數的大小，此時三角晶格中圓形的大小和位置會發生改變。對不同參數取值下的能帶結構進行仿真，結果如圖3所示，當a0/R=3.125 時，帶隙歸一化頻率在0.48～0.51之間；當a0/R=3 時，帶隙完全消失；當a0/R=2.8 時，帶隙歸一化頻率在0.44～0.48 之間。3 種情況下的計算結果均和文獻[14]中的仿真結果一致，并且仿真所用時間比采用常見三角晶格進行仿真時間更短、效率更高。

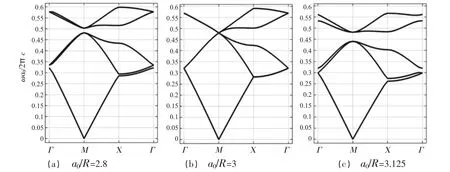
圖3 二維蜂窩狀光子晶體的TM 模式的能帶圖

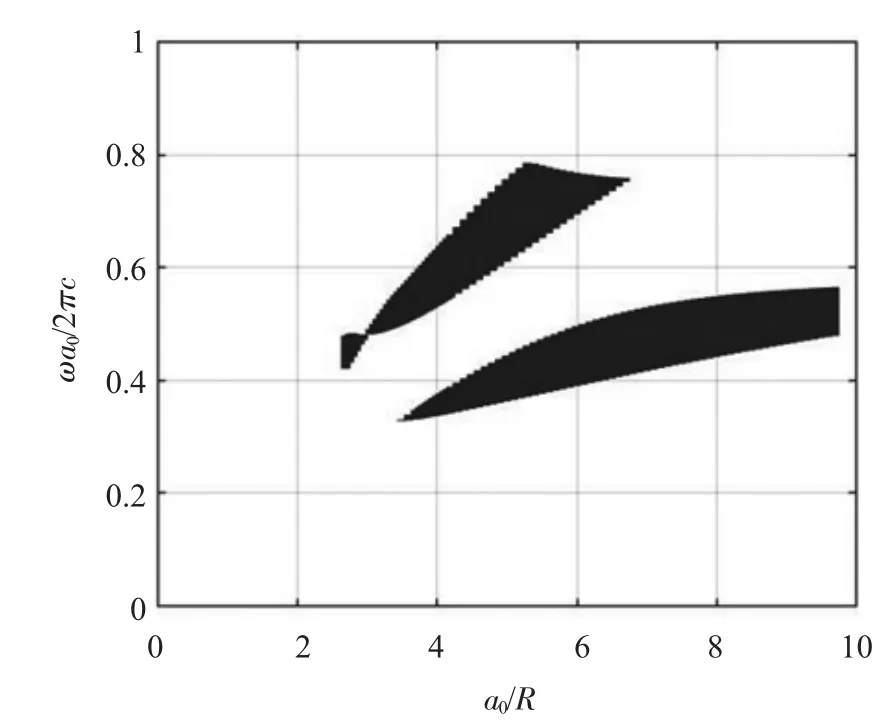
圖4 TM 模式下改變晶格參數的Gap map 變化

2.2 算例2：二維新結構蜂窩狀光子晶體仿真

下面，研究當改變2.1 節中晶格結構時光子晶體的能帶結構。在每個六角蜂窩晶格的中心加入材質為Si（介電常數為17.64），半徑r 同樣為d/2 的介電圓柱，周圍背景為空氣介電常數εa=1，周圍的圓柱介電常數仍為εb=11.7，每個晶格中中心圓柱的介電常數為εc=17.64，其余參數不變，對這種新結構進行仿真。新結構蜂窩狀光子晶體示意圖如圖5 所示。

圖5 新結構蜂窩狀光子晶體示意圖

取晶格參數a0/R=3 時為例，由2.1 節可知圖1 所示的蜂窩狀光子晶體在此晶格參數條件下并無任何帶隙產生，而新結構的能帶結構如圖6 所示，此時會產生1 條新的帶隙，與2.1 節中結構相比新結構光子晶體產生的帶隙位置向低頻方向移動。此時產生的帶隙歸一化頻率范圍為[0.264 954 9，0.279 614 2]，寬度為0.014 659 2。

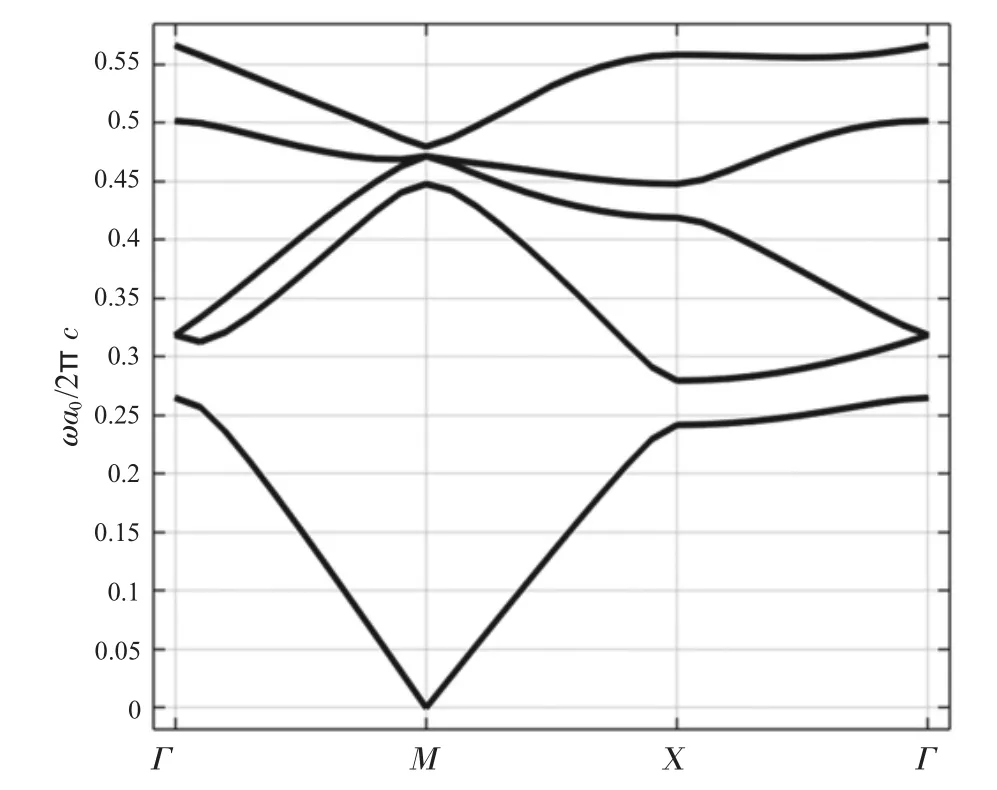
圖6 新結構蜂窩狀光子晶體得到的能帶圖

為探究新結構的帶隙隨參數的變化情況，類似2.1節中保持其他參數不變僅改變晶格參數a0/R，a0/R 的取值從2.7～7.7，得到新結構TM 模式下蜂窩狀光子晶體的帶隙變化圖，如圖7 所示。由圖7 可知，當晶格參數a0/R=5.6 時可產生最寬帶隙，此時有3 條帶隙，寬度分別為0.037 548，0.002 096 和0.134 911。

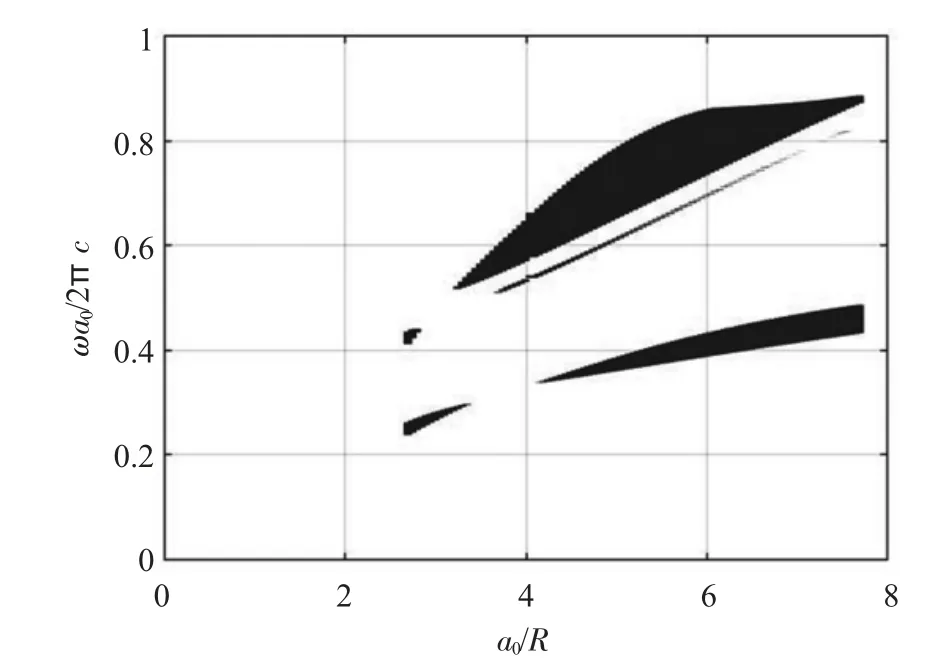
圖7 改變晶格參數a0/R 得到的Gap map

為進一步探究蜂窩狀光子晶體帶隙的產生和變化情況，改變蜂窩晶格中心處介質圓柱的截面半徑r，得到帶隙變化如圖8 所示，當r 取0.75d 時可獲得最寬的帶隙，此時有4 條帶隙存在。

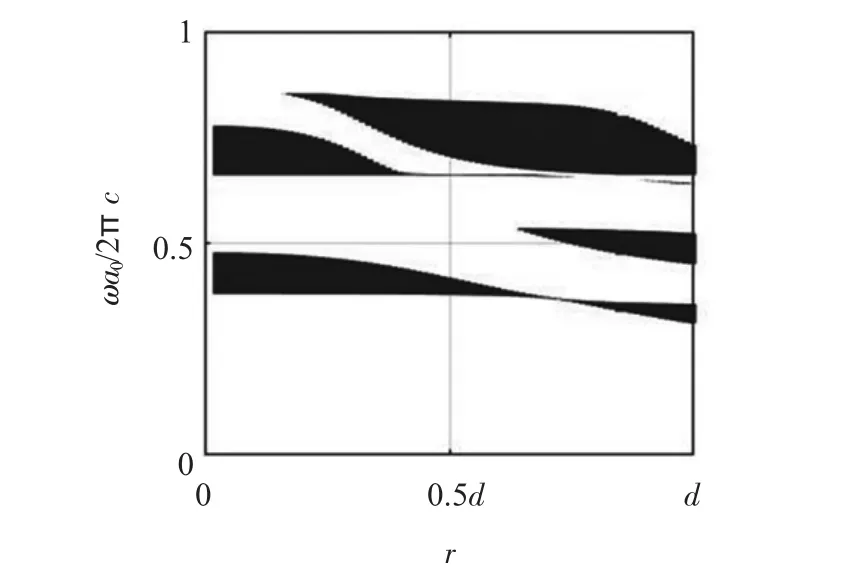
圖8 改變中心圓柱截面半徑r 得到的Gap map

2.3 算例3：二維蜂窩狀復合膠體光子晶體仿真

當前的光子晶體能帶研究主要是針對人為可控的物理參數的對比研究，但是對于不同尺寸粒子混合形成的膠體光子晶體的光子帶隙則少有研究。膠體光子晶體是一類利用交替納米顆粒通過自組裝而成的周期有序結構的材料，可以保留2 種材料的光學特性，具有制備簡單、易于實現功能化和成本低廉等優勢，可應用于傳感器、防偽圖案和顯示器件等領域。這種光子晶體由于其獨特的結構特征及光學特性的廣泛應用，近年來已成為光子晶體領域的研究熱點。

采用這種新型材料，由大粒徑聚苯乙烯（PS）和小粒徑二氧化硅（SiO2）組成二維復合膠體光子晶體，其結構如圖9 所示，背景介質為空氣εa=1；在此種結構中大的微球（PS）介電常數為2.53，半徑為d/2；小的微球（SiO2）介電常數為2.13，其半徑為r=d/4。本文基于有限元法，利用COMSOL 軟件的波動光學模塊建立光子晶體模型，并使用Floquet 周期性邊界條件，探究不同參數下膠體光子晶體的帶隙寬度。

利用COMSOL 軟件對圖9 所示的膠體光子晶體的光子帶隙進行了仿真模擬，結果如圖10 所示，此時在[0.847 558 0，0.840 933 8]的歸一化頻率的區間產生一條寬度為0.006 624 2 的帶隙。

圖9 由PS 和SiO2 組成的二維復合膠體光子晶體結構

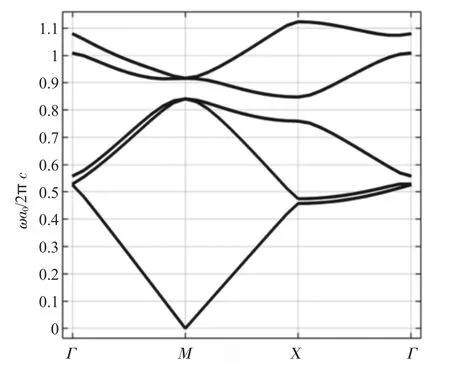
圖10 二維復合膠體光子晶體仿真結果圖

采用二維復合膠體光子晶體可以產生如上所述的帶隙，而如果僅使用一種材料PS，此時能帶結構無任何帶隙產生，如圖11 所示。由此可見，引入二維復合膠體材料能有效地增大蜂窩狀光子晶體的帶隙寬度，同時還可以保留2 種材料的光學特性。

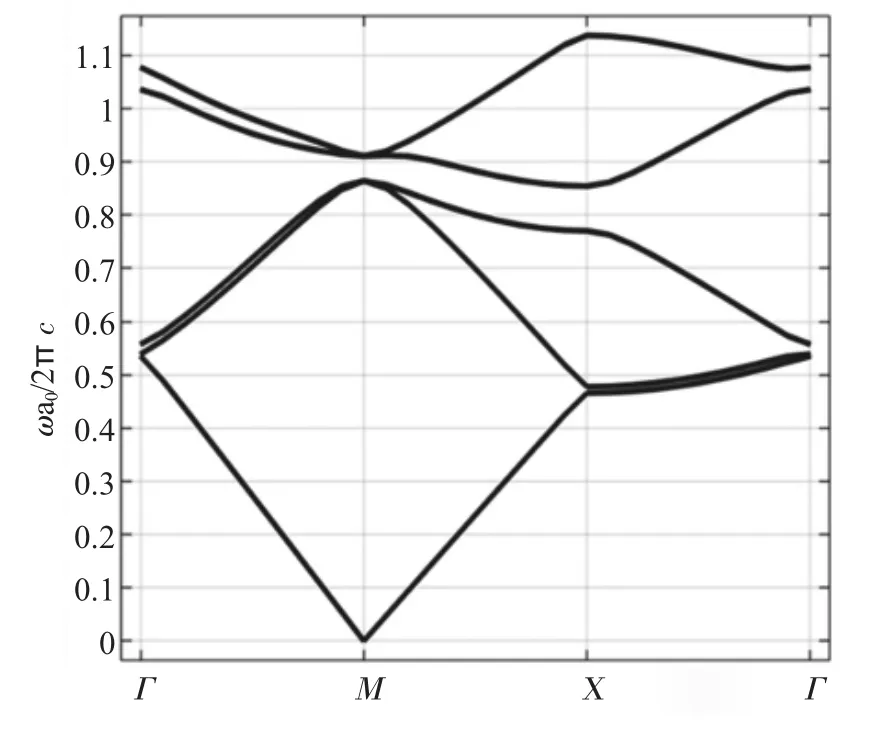
圖11 僅由PS 材料構成的光子晶體能帶圖

取上面討論的最佳參數：晶格常數選取a0/R=5.6，中心圓柱界面半徑r 取0.75d 時，可獲得寬帶隙，此時應用新材料的蜂窩狀光子晶體的能帶圖如圖12 所示，此時會產生3 條帶隙。第一條帶隙的歸一化頻率范圍為[0.467 225，0.487 643]，帶寬為0.020 717；第二條帶隙的歸一化頻率范圍為[0.827 783，0.831 438]，帶寬為0.003 655；第三條帶隙的歸一化頻率范圍為[0.929 49，0.953 844]，帶寬為0.024 347。由圖10 和圖12 比較可知，選取合適的晶格參數a0/R 和圓形半徑r來獲得寬帶隙的方法是有效的。

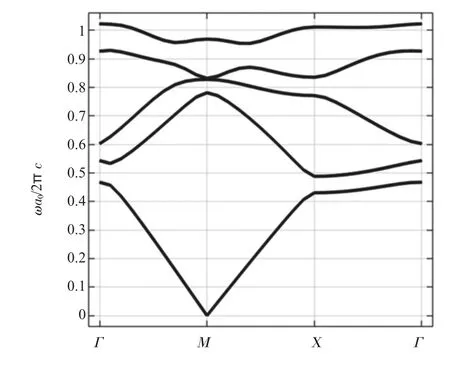
圖12 最優參數下二維復合膠體光子晶體仿真結果圖

3 結論

本文采用了有限元方法,研究了二維蜂窩狀光子晶體的能帶結構數值模擬和寬帶隙的結構設計問題。對有限元方法和COMSOL 軟件的結合運用，使得光子晶體能帶結構的求解變得簡單高效。數值模擬方法是新材料運用、新結構設計的一種非常高效、便捷的方法，通過優化蜂窩狀光子晶體的晶格參數及應用新材料，基于數值模擬方法探究了二維蜂窩狀光子晶體的參數與帶隙的關系，通過選取最佳參數構造了寬帶隙的新型二維蜂窩狀光子晶體結構。本文的研究為二維蜂窩狀光子晶體的能帶結構求解提供了一種有效求解途徑，有望為光子晶體設備的制備提供指導和數值算法支撐。